BROADCAST NEWS PHONEME RECOGNITION

BY SPARSE CODING

Joseph Razik

, S´ebastien Paris

and Herv´e Glotin

LSIS/DYNI, Universit´e du Sud Toulon-Var, Avenue de l’Universit´e - BP20132, 83957 La Garde Cedex, France

LSIS/DYNI, Universit´e Aix-Marseille, Domaine universitaire de Saint J´erˆome, Avenue Escadrille Normandie Niemen,

13397 Marseille Cedex 20, France

Keywords:

MFCC, GMM, Sparse coding, Large-scale SVM, Explicit feature maps.

Abstract:

We present in this paper a novel approach for the phoneme recognition task that we want to extend to an

automatic speech recognition system (ASR). Usual ASR systems are based on a GMM-HMM combination

that represents a fully generative approach. Current discriminative methods are not tractable in large scale

data set case, especially with non-linear kernel. In our system, we introduce a new scheme using jointly

sparse coding and an approximation additive kernel for fast SVM training for phoneme recognition. Thus, on

a broadcast news corpus, our system outperforms the use of GMMs by around 2.5% and is computationally

linear to the number of samples.

1 INTRODUCTION

In recent years major advancements have been

achieved in speech processing. However, robust

speech recognition still remains a challenging task.

Current systems are still exhibiting difﬁculties when

dealing with real-life conditions such as: multiple-

speakers without training, noise, background music,

spontaneous speech. The most common architecture

of an automatic speech recognition (ASR) system is

based on a generative framework and more specially

a GMM-HMM approach (Gaussian Mixture Model -

Hidden Markov Model). Prior to fully decoding sen-

tences, a kind of phoneme recognition module is the

ﬁrst and most crucial part of the ASR system.

The latter is usually modeled by a GMM with a

given number of components, large enough to capture

the intra-variability of the phonemes (Huang et al.,

2001). It assumes that the conditional pdf to each

phoneme’s class has a parametric form and that is

comprised a mixture of normal pdfs. In practice, this

strong assumption is mainly veriﬁed when training

data is sufﬁciently available, but can introduce some

over-ﬁtting for less populated classes.

Recently, in vision systems, discriminative ap-

proaches combining bag-of-features and large-scale

classiﬁers have shown dramatic improvement versus

generative methods (Yang et al., 2009). These new

approaches relie on three basic ingredients: (i) an un-

supervised data encoding, (ii) feature extraction from

a learned dictionary with pooling, and (iii) fast SVM

(Support Vector Machines) for classiﬁcation.

For the ﬁrst step, sparse learning (see in (Lin et al.,

2008; Hsieh et al., 2008; Wang et al., 2010; Smit and

Barnard, 2009; Sivaram et al., 2010; Mairal et al.,

2010)) allows a smaller re-construction error with few

basis vectors, involving discriminative vectors’ dic-

tionary properties. After applying sparse code pool-

ing, we obtain features descriptors with only positive

or null values. In this case, specialized kernels such

as intersection histogram kernel, offer the state of the

art classiﬁcation performances (Maji et al., 2009). In

(Vedaldi and Zisserman, 2011), such kernels can be

efﬁciently approximated via the feature map frame-

work, involving fast training (linear in number of

training samples (Fan et al., 2008)).

In this paper, we propose a new phoneme recogni-

tion system based on MFCC (Mel Frequency Cepstral

Coefﬁcient) sparse coding and fast non-linear train-

ing.

First, in section 2 we will describe the audio

MFCC parameters as our input features, then in sec-

tion 3 we present a short overview of the GMM. Sec-

tion 4 provides an introduction of the sparse coding

framework. Pooling methods are presented in section

5. The large-scale linear SVM is reviewed in section

6 with also the feature maps homogeneous additive

kernel approximation method. Finally, sections 7 and

191

Razik J., Paris S. and Glotin H. (2012).

BROADCAST NEWS PHONEME RECOGNITION BY SPARSE CODING.

In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 191-197

DOI: 10.5220/0003778201910197

 SciTePress

8 are dedicated to corpus presentation and results.

2 PARAMETERS

The parameters extracted from the audio signal are

based on MFCC (Mel Frequency Cepstral Coefﬁ-

cients) (Davis and Mermelstein, 1980; Rabiner and

Juang, 1993) with CMS (Cepstral Mean Subtraction)

normalization. The frame-shift for their computation

is 10 ms.

Additionally to the static MFCC coefﬁcients (C

...C

), we compute also dynamic information val-

ues as their ﬁrst derivative and variance. More pre-

cisely, we compute and concatenate to the ﬁnal pa-

rameter vector the variance, and several approximated

derivative coefﬁcients according to the ranges be-

tween points for this calculation (20, 62, 125 and 250

ms). The usual approximation at time t is done by re-

gression with coefﬁcients at t − α and t + α (Young

et al., 1995). Moreover, two size of the analysis win-

dow is used for the computation of the MFCC (16

and 32 ms). Thus, the ﬁnal parameter vector is the

concatenation of each kind of parametrization and its

total dimension is 260, 13 statics and 13 dynamics by

5 kinds of dynamic coefﬁcients and 2 window sizes.

2.1 Whitening

Several pre-processing methods of the parameter vec-

tors could be applied in order to have the data better

conditioned. The ﬁrst simple pre-processing step is

to center the data, i.e. to make the mean of the pa-

rameter vector equals zero. In fact, the static MFCC

coefﬁcients are already computed as centered with the

CMS normalization but the dynamic coefﬁcients are

not.

In a second step, the entire data set of the vec-

tors may be whitened. This process is commonly

used in deep learning domain but not so frequently

in speech recognition (Ranzato et al., 2010). The

whitening process consists in decorrelating the data

and making their variances equal to unity by the use

of an eigen-value decomposition (EVD) (Hyv¨arinen

and Oja, 2000).

More precisely, if we called X the set of parameter

vectors, X is then linearly transformed into a whiten

set

X with the property that E{

} = Id, the iden-

tity matrix. By using an EVD decomposition of the

preceding covariance matrix, we obtain the relation

} = E∆E

, where E is the orthogonal matrix

of eigenvectors of E{

} and ∆ is the diagonal ma-

trix of its eigenvalues: ∆ = diag(δ

,.. ., δ

). The es-

timation of the whiten vectors ˜x can now be obtained

by the following equation:

˜x = E∆

−1/2

x (1)

where ∆

−1/2

= diag(δ

−1/2

,.. .,δ

−1/2

Thus, besides the raw parameter vectors we assess

the use of a whitening process on our MFCC data and

the impact on the recognition rate.

3 BASELINE SYSTEM: GMM

We compare our phoneme recognition method to one

based on Gaussian Mixture Models (GMM) that is

considered as a reference system in phoneme recog-

nition task.

GMMs are used as a generative classiﬁer model-

ing data classes as a mixture of M Gaussian pdfs and

expressed as:

G(x|y;θ) =

∑

i=1

N (x,µ

,Σ

∑

i=1

= 1 (2)

for which, with vectors of n dimensions, the continu-

ous pdf is deﬁned as:

N (x,µ,Σ) ,

(2π)

det(Σ)

exp(−

(x−µ)

−1

(x−µ)).

(3)

The w

coefﬁcients represent the weights of

each Gaussian pdf composing the conditional pdf

G(x|y;θ). For each class y = j, j = 1, .. .,V, the

training process consists in learning parameters θ

j,i

,µ

j,i

,Σ

j,i

}, i = 1,.. .,M by an EM algorithm

(Huang et al., 2001) and particularly with the HTK

software (Young et al., 1995). Moreover, to avoid

over-ﬁtting we assume during the GMMs training that

the covariances matrices Σ

j,i

are diagonals and we

add an extra regularization term. For all the V = 41

classes, we will learn the conditional pdf G(x|y;θ)

by varying the number of components that maximizes

the accuracy, from M = 1 to M = 256.

4 FROM VECTOR

QUANTIFICATION TO SPARSE

CODING

Super-vectors coupled with a supervised training al-

gorithm represents a promising discriminating ap-

proach (Arous and Ellouze, 2003; Tomi Kinnunen,

2010). We propose to build such super-vectors us-

ing sparse coding and a pooling procedure. Let X

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

192

be the set of n × N-dimensional MFCC matrix ex-

tracted from the audio, i.e. X , [x

,.. .,x

] ∈ R

n×N

Let D be a dictionary made of K vectors such D ,

,.. .,d

] ∈ R

n×K

and trained from data. This dic-

tionary clusters/resumes all data X into K codebook

vectors.

From this trained D, in the traditional vector quan-

tization (VQ) approach, each vector x

of X is as-

signed to only one d

such that:

= argmin

k=1,...,K

− d

(4)

Let be C = [c

,.. .,c

] ∈ R

n×K

the VQ matrix for

which each c

vector has only one component c

6= 0

(corresponding to the d

codebook vector from the

preceding equation (4). The associated VQ optimiza-

tion problem is formulated as follows:

argmin

D,C

∑

i=1

− Dc

s.t. kc

ℓ

= 1,∀i (5)

where kxk

ℓ

designs the pseudo zero-norm, i.e. only

one element of x is equal to 1, others are set to 0. In

equation (5), D,C must be optimized jointly by the

Kmeans algorithm or variants for example.

In the sparse coding (SC) approach, the difference

is that each vector x

can be expressed as a linear com-

bination of the vectors of the dictionary D and not

only by one of it. Then, the problem to solve is ex-

tended as in the following equation:

argmin

D,C

∑

i=1

− Dc

+ λkc

ℓ

s.t. kc

ℓ

= 1

(6)

The regularization term λ coupled with the ℓ

norm, as seen in the equation (6), ensures the spar-

sity of the optimized codes. Unfortunately, this joint

constrained optimization does not have a convex ex-

plicit formulation and the resolution is done in two

steps, repeated iteratively until convergence.

The ﬁrst step consists in updating the current es-

timation of the dictionary

t+1

given current sparse

codes

via a block coordinate descent optimizer.

The second step consists in updating sparse codes

t+1

given the current dictionary

t+1

via a LASSO

algorithm (Mairal et al., 2009).

5 SPARSE CODES POOLING TO

CONSTRUCT A NEW AUDIO

DESCRIPTOR

Each phoneme realization p

, i = 1,. ..,P, where P

deﬁnes the total number of phonemes in the data set,

is associated with F

MFCC vectors x

, l = 1,.. .,F

(of dimension n = 260 and such that

∑

i=1

= N, the

total number of audio parameter vectors). In order

to construct the new proposed audio feature vector

= [z

,.. .,z

] for this phoneme, all associated sparse

codes {c

}, l = 1, .. .,F

are projected/pooled by one

of the two following methods:

• Mean pooling:

∑

l=1

| (7)

• Max pooling:

= max(|c

|,.. ., |c

|) (8)

The set of the P features {z

} and their correspond-

ing label will be trained efﬁciently with a large-scale

linear SVM. Since sparse dictionary learning coupled

with max-pooling method produce almost perfectly

linear separable descriptors, a fast linear SVM solver

such as Liblinear is preferred. This approach can be

perceived discriminative since we don’t focus on the

data densities to classify, but only on the frontiers of

separation.

6 LARGE-SCALE LINEAR

SUPPORT-VECTOR MACHINE

Once the descriptors are computed, a large-scale lin-

ear SVM can be used as classiﬁer. For training

the model efﬁciently, according to the Vapnik the-

ory (Vapnik, 1998), we aim to minimize the structural

error in order to generalize performances on unseen

data. This leads to ﬁnd a binary classiﬁer separating

classes based on the maximum margin principle. Sev-

eral algorithms exist that aim to ﬁnd models maximiz-

ing such margins, for example neural networks with

Generalized Relevance Learning Vector Quantization

(GLRVQ) (Hammer et al., 2004), some variant of ad-

aboosting (Rudin et al., 2007) and the popular SVM

(Vapnik, 1998). A ﬁner analysis indicates that the

second error term of the total risk’s upper bound is in-

creasing when the Vapnik-Chervonenkis (VC) dimen-

sion ~ is also increasing. This latter is directly linked

BROADCAST NEWS PHONEME RECOGNITION BY SPARSE CODING

193

with the particular choice of the kernel, ~ = 2K + 1

for linear kernel and ~ = ∞ for RBF kernel. In other

words, one may prefer a simple linear separator espe-

cially when the input feature dimension K is high. It

will generally perform close to those obtained with a

non-linear specialized kernel but with faster training

and prediction.

SVM is trained classically with the Sequential

Minimal Optimization (SMO) algorithm (Sch¨olkopf

et al., 2001) with a complexity O(KP

) where P is

the number of training examples (in the worst case,

when P

= P, P

is the number of support vectors).

This quadratic dependency from P can be reduced if

we particularize kernels to linear ones and by intro-

ducing an extra tolerance term ε in the minimization

problem. This leads to large-scale linear SVM solvers

based on efﬁcient Newton optimizers (Hsieh et al.,

2008) or stochastic gradient descent (on the primal

form, see (Shalev-Shwartz et al., 2007)). Complexity

of such a large-scale solver is reduced to O(KP).

Let us deﬁne the set of sparse code descriptors

(after mean- or max-pooling) Z , {z

,.. .,z

} and

their corresponding labels y , {y

,.. .,y

} where z

∈

Z ⊆ R

and y

∈ {−1,1}. Thus, each phoneme

recognition is considered as a class/non-class prob-

lem with a one-against-all approach. P corresponds

to the number of phoneme realizations, which is in-

ferior to the total number N of MFCC parameter vec-

tors and equals the number of descriptors after pool-

ing method.

The linear SVM problem consists of ﬁnding the

hyperplane parameter bw minimizing the sum of a ℓ

loss function and a ℓ

regularization term such that:

= argmin

(

w+C

∑

i=1

max



1− y



)

(9)

To solve this problem, we use a modiﬁed version

of the liblinear 1.5 package (Fan et al., 2008) accept-

ing dense input vectors

. Any new input vector y

will be classiﬁed as bz = sign( f(z; bw)) = sign(bw

z) ∈

{−1, 1} by a simple scalar product in O(K).

6.1 Fast Non-linear Method for

Approximated Additive

Homogeneous Kernels via Explicit

Feature Maps

For linear SVM, evaluation is performed with a

simple scalar product f

(z;w) = w

z taking O(K)

Available at http://www.cs.berkeley.edu/?smaji/projects

/digits/.

whereas for non-linear kernel the expansion be-

comes f

(z;β) =

∑

i=1

K(z,z

) taking approximately

O(KP

). Both for training and predicting, SVM with

non-linear kernels is at least P

slower.

First introduced by (Maji et al., 2009) for the

intersection histogram (IH) kernel and extended to

any homogeneous additive kernels (IH, χ

, Shannon-

Jensen) in (Vedaldi and Zisserman, 2011), an ex-

plicit closed form of the feature maps associated to

these kernels, denoted Ψ(z), permits the approxima-

tion f

(z) ≈ w

′T

Ψ(z) = w

′T

′

. Moreover the Ψ(z)

approximation is independent of the training data.

Now w

′

and z

′

∈ R

(2v+1)K

where v is the approxi-

mation order (typically v = {1,2}) and f

(z) runs in

O((2v+ 1)K).

Assuming z

is the j

components of z, j =

1,.. .,K then for any homogeneous kernel, Ψ(z

) is

approximated as follows:

) =











i = 0,

i+1

cos



i+1

Llogz



i > 0 odd,

sin



Llogz



i > 0 even,

(10)

is the i

value of the spectrum κ(ω) sampled

with a sampling frequency equal to L. Closed forms

of κ(ω) depend on the chosen kernel type and read-

ers can retrieve details in (Vedaldi and Zisserman,

2011). For an efﬁcient implementation, Vedaldi also

proposes to pre-compute values of

) for wide

dynamic of z

and store them in a table. With this

approach, retrieving

) with this given table runs

in O(2ν+ 1).

Since it takes an extra O((2v + 1)K) to compute

Ψ(z) from z, total run time for using an additive

homogeneous kernel is O(2(2v + 1)K) (Ψ(z)+f

(z)

computation) and even more important is independent

of P

and consequently of the training size P. The ac-

celeration is proportional to

2(2v+1)

for the non-linear

case.

To make experimentations, we used a modiﬁca-

tion of the Scenes/Objects Classiﬁcation Matlab tool-

box framework which implements all the above men-

tioned processing (Paris, 2011).

7 CORPUS DESCRIPTION

To develop our method, we used about 2 hours of

French radio broadcast news. This corpus was ex-

tracted from a larger broadcast news corpus pro-

vided by the 2006 ESTER French evaluation cam-

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

194

paign (Gravier et al., 2004; Galliano et al., 2006;

Razik et al., 2011). This corpus contains only broad-

band speech (no narrow band, no music segments)

and sentence level transcriptions are provided. How-

ever, some sentences may have background noise or

music. There are 72 speakers in the 2 hours, 28 fe-

males and 44 males. This corpus is more difﬁcult and

more realistic (noise, number of classes, etc.) than the

usual TIMIT data set.

In our study, we work at phoneme level, so we

used a forced alignment process of the data by exter-

nal acoustical models and lexicon of a large vocab-

ulary speech recognition systems (Illina et al., 2004).

We used a decomposition onV = 41 french phonemes

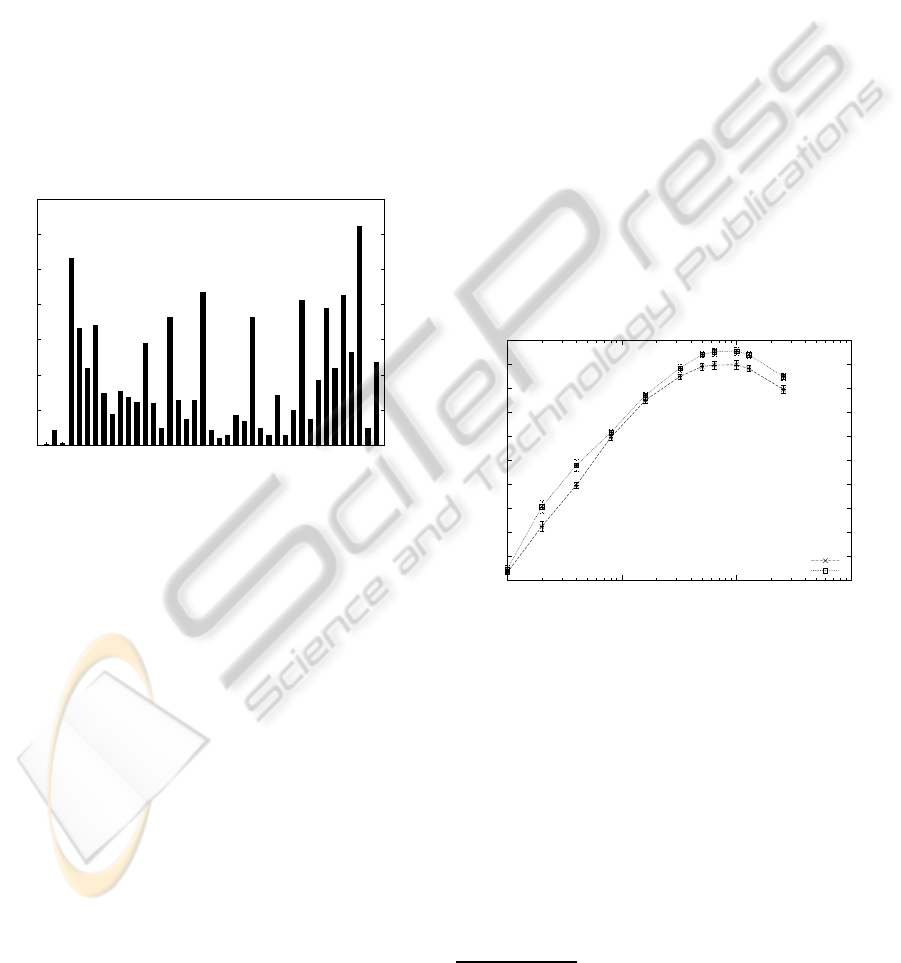
including silence and short pause. Figure 1 shows the

histogram of the phoneme distribution within the 2

hours of our corpus.

1000

2000

3000

4000

5000

6000

7000

R_l

sil

z_l

t_l

n_l

euf

swa

# Occurrences

Phonemes

Figure 1: Phoneme distribution in the corpus.

As with this corpus some phonemes are underrep-

resented, we will use a cross validation technique in

10 subsets to assess the performance of both devel-

oped systems instead of ﬁxed training, development

and test corpora. One of the ten subset was used as a

development corpus to tune the hyperparameter of the

SVM.

The subsets were not deﬁned or clustered ac-

cording to the speakers thus forthcoming results are

speaker independent.

According to the corpora size, the different results

are given in recognition rate and standard deviation

(vertical bars in ﬁgures), and to a signiﬁcance conﬁ-

dence of around 0.2% at 0.95 level of signiﬁcance.

8 RESULTS

As the corpus is labeled in 41 phoneme classes, we

learn 41 GMM models (one model for each phoneme)

with various number of components. We use the HTK

toolkit (Young et al., 1995) for extracting both the

MFCC coefﬁcients and training the GMM models

We assess a number of Gaussian mixtures vary-

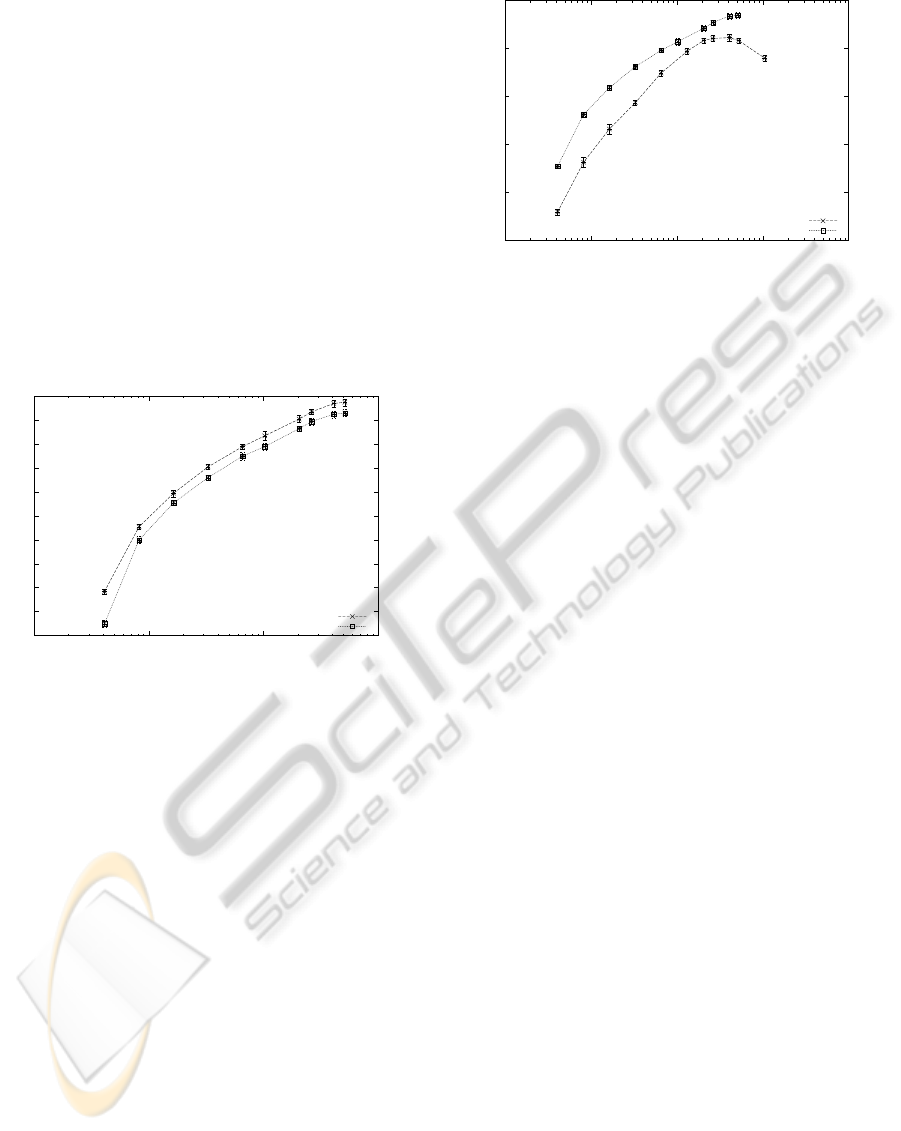
ing between 1 to 256. Figure 2 shows that the GMM

system obtained a best performance of about 61% of

accuracy for 100 mixtures on our corpus. This perfor-

mance is of good level knowing that our corpus can be

considered difﬁcult (only 1h of training data, broad-

cast radio condition).

8.1 Whitening The Data

Additionally to the comparison between GMM and

SC/SVM model, we assess the use of a whitening pre-

processing of the MFCC data as explained in section

2.1.

Figure 2 shows the accuracy rate of the GMM

phoneme recognition system according to the number

of mixtures for both raw and whiten MFCC data. As

for the case of image processing (Coates et al., 2011),

whitening the data before computing both GMM or

Sparse Dictionary improves the results by around 1%

in absolute.

1 10 100 1000

Accuracy [%]

Number of mixtures

No Whitening

Whitening

Figure 2: Effect of whitening with GMM according to the

number of mixtures (log scale).

8.2 Sparse Coding/SVM

In the SC/SVM based system, we assess the role of

several parameters on the accuracy as the choice of

the pooling method, the use of linear or non-linear

kernel (intersection kernel) for the SVM and of course

the size of the dictionary.

Concerning the recognition system process, the

SVM hyper-parameter is tuned globally on all

phoneme classes and not speciﬁcally to each class.

Moreover, the descriptor vectors (sparse codes) are

However we do not use the Hidden Markov Model

(HMM) capability of HTK and trained our GMM by a one

state HMM.

BROADCAST NEWS PHONEME RECOGNITION BY SPARSE CODING

195

normalized according to the kernel type. In the linear

case, the vectors should be ℓ

normalized, and in the

non-linear case, the vectors should be ℓ

normalized

(Vedaldi and Zisserman, 2011).

In our experiment, the system obtains the same ac-

curacy performance whatever which pooling method

is used.

As we mentioned, the use of an approximated

non-linear kernel SVM improves the accuracy of our

system compared to the linear case. Figure 3 shows

the accuracy of both linear and intersection kernels.

We can note that the approximated non-linear system

performs better than the linear one. Even if their ac-

curacy are close, the difference between both is sig-

niﬁcant and the training time is just slightly increased

by 2ν+ 1 where ν = 1 in our study.

10 100 1000 10000

Accuracy [%]

Dictionary size

approximated IH kernel

linear kernel

Figure 3: Accuracy with linear and approximated IH kernel

(ν = 1) in log scale.

8.3 GMM vs. Sparse Coding

We compare both GMM and Sparse Coding based

systems on the corpus. In order to compare their re-

sults, we consider that a GMM with M mixtures is

similar to a codebook dictionary with K = 41 × M

vectors (number of classes by number of mixtures).

Figure 4 shows the accuracy of both system ac-

cording to this comparison scale. The SC/SVM

based system outperforms the GMM based system by

around 2.5% in absolute (63.5% for the Sparse Cod-

ing/SVM and 61.1% for the GMM) at their best.

9 CONCLUSIONS AND

PERSPECTIVES

In this paper we showed that the sparse coding ap-

proach outperforms signiﬁcantly the classic GMM.

For any number of Gaussian components, the system

10 100 1000 10000 100000

Accuracy [%]

Dictionary size

GMM system

SC/SVM system

Figure 4: Accuracy of SC/SVM vs. GMM (log scale).

using the equivalent number of sparse codes outper-

forms the GMM. An advantage of the sparse coding

method is that it needs less training samples to learn

a representative dictionary and the representation is

more compact. The GMM method is more sensitive

to the total amount of available data and to the initial-

ization step. Moreover, in this paper we achieved re-

sults close to a specialized non-linear kernel thanks to

the additive homogeneous kernel approximation, still

linear in computation time.

Several directions could be explored to further im-

prove the performance of the sparse approach, includ-

ing Laplacian constraints in the sparse codes con-

struction to obtain a more reliable codebook versus

a slight change in the data (Wang et al., 2010), us-

ing a hierarchical construction of the codebook (Yu

et al., 2011), or providing a feature selection method

based on MKL (Multiple Kernel Learning) (see FGM

– Feature Generating Machine algorithm (Tan et al.,

2010)). Although we used an unsupervised method

for building the codebook, it is also possible to train

simultaneously the dictionary and the classiﬁer in a

supervised way (Mairal et al., 2008).

Furthermore, the results obtained in this study are

only focused on the phone stage of speech recogni-

tion. We should evaluate the impact of the improve-

ment at this level on the ﬁnal word recognition rate

of a complete ASR system. However, the ASR sys-

tem can still be based on an HMM classiﬁer with the

observation matrix directly build with the probability

outputs of the SVM. It has the advantage of being a

method both generative and discriminative. Finally,

as it has been introduced more recently, it is possible

to use a structural SVM learning discriminately and

simultaneously the temporal structure and the sparse

codes in linear time (Joachims et al., 2009).

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

196

REFERENCES

Arous, N. and Ellouze, N. (2003). Cooperative supervised

and unsupervised learning algorithm for phoneme

recognition in continuous speech and speaker-

independent context. Neurocomputing, 51:225–235.

Coates, A., Lee, H., and Ng, A. Y. (2011). An analysis of

single-layer networks in unsupervised feature learn-

ing. In Artiﬁcial Intelligence and Statistics (AISTATS),

page 9.

Davis, S. and Mermelstein, P. (1980). Comparison of para-

metric representations for monosyllabic word recog-

nition in continuously spoken sentences. IEEE Trans.

ASSP, 28:357–366.

Fan, R.-E., Chang, K.-W., Hsieh, C.-J., Wang, X.-R., and

Lin, C.-J. (2008). LIBLINEAR: A library for large

linear classiﬁcation. Journal of Machine Learning Re-

search, 9:1871–1874.

Galliano, S., Geoffrois, E., Gravier, G., Bonastre, J.,

Mostefa, D., and Choukri, K. (2006). Corpus descrip-

tion of the ester evaluation campaign for the rich tran-

scription of french broadcast news. In LREC, pages

315–320.

Gravier, G., Bonastre, J., Galliano, S., and Geoffrois, E.

(2004). The ester evaluation compaign of rich tran-

scription of french broadcast news. In LREC.

Hammer, B., Strickert, M., and Villmann, T. (2004). Rel-

evance lvq versus svm. In Artiﬁcial Intelligence and

Softcomputing, springer lecture notes in artiﬁcial in-

telligence, volume 3070, pages 592–597. Springer.

Hsieh, C.-J., Chang, K.-W., Lin, C.-J., and Keerthi, S. S.

(2008). A dual coordinate descent method for large-

scale linear svm.

Huang, X., Acero, A., and Hon, H. (2001). Spoken Lan-

guage Processing: A Guide to Theory, Algorithm and

System Development. Prentice Hall.

Hyv¨arinen, A. and Oja, E. (2000). Independent component

analysis: algorithms and applications. Neural Netw.,

13:411–430.

Illina, I., Fohr, D., Mella, O., and Cerisara, C. (2004). The

automatic news transcription system : Ants, some real

time experiments. In ICSLP, pages 377–380.

Joachims, T., Finley, T., and Yu, C.-N. (2009). Cutting-

plane training of structural svms. Machine learning,

77(1):27–59.

Lin, C.-J., Weng, R. C., and Keerthi, S. S. (2008). Trust

region newton method for logistic regression. J. Mach.

Learn. Res., 9.

Mairal, J., Bach, F., Ponce, J., and Sapiro, G. (2009). On-

line dictionary learning for sparse coding. In Proceed-

ings of the 26th Annual International Conference on

Machine Learning, ICML ’09, pages 689–696, New

York, NY, USA. ACM.

Mairal, J., Bach, F., Ponce, J., and Sapiro, G. (2010). On-

line learning for matrix factorization and sparse cod-

ing. Journal of Machine Learning Research, 11:19–

60.

Mairal, J., Bach, F., Ponce, J., Sapiro, G., and Zisserman,

A. (2008). Supervised dictionary learning. Advances

Neural Information Processing Systems, pages 1033–

1040.

Maji, S., Berg, A. C., and Malik, J. (2009). Classiﬁcation

using intersection kernel support vector machines is

efﬁcient. In CVPR.

Paris, S. (2011). Scenes/objects classiﬁcation toolbox.

http://www.mathworks.com/matlabcentral/ﬁleexchan

ge/29800-scenesobjects-classiﬁcation-toolbox.

Rabiner, L. and Juang, B. (1993). Fundamentals of Speech

Recognition. Prentice Hall PTR.

Ranzato, M., Krizhevsky, A., and Hinton, G. (2010). Fac-

tored 3-way restricted boltzmann machines for mod-

eling natural images. In International Conference on

Artiﬁcial Intelligence and Statistics AISTATS.

Razik, J., Mella, O., Fohr, D., and Haton, J.-P. (2011).

Frame-synchronous and local conﬁdence measures

for automatic speech recognition. IJPRAI, 25(2):157–

182.

Rudin, C., Schapire, R. E., and Daubechies, I. (2007). Anal-

ysis of boosting algorithms using the smooth margin

function. The Annals of Statistics, 35(6):2723–2768.

Sch¨olkopf, B., Platt, J. C., Shawe-Taylor, J. C., Smola, A. J.,

and Williamson, R. C. (2001). Estimating the support

of a high-dimensional distribution. Neural Comput.,

13:1443–1471.

Shalev-Shwartz, S., Singer, Y., Srebro, N., and Cotter, A.

(2007). Pegasos: Primal estimated sub-gradient solver

for svm.

Sivaram, G., Nemala, S., M. Elhilali, T. T., and Hermansky,

H. (2010). Sparse coding for speech recognition. In

ICASSP, pages 4346–4349.

Smit, W. J. and Barnard, E. (2009). Continuous speech

recognition with sparse coding. Computer Speech and

Language, 23:200–219.

Tan, M., Wang, L., and Tsang, I. W. (2010). Learning sparse

svm for feature selection on very high dimensional

datasets. In ICML, page 8.

Tomi Kinnunen, H. L. (2010). An overview of text-

independent speaker recognition: From features to su-

pervectors. Speech Communication, 52:12–40.

Vapnik, V. N. (1998). Statistical Learning Theory. Wiley-

Intersciences.

Vedaldi, A. and Zisserman, A. (2011). Efﬁcient additive

kernels via explicit feature maps. IEEE PAMI.

Wang, J., Yang, J., Kai Yu, F. L., Huang, T., and Gong, Y.

(2010). Locality-constrained linear coding for image

classiﬁcation. CVPR’10.

Yang, J., Yu, K., Gong, Y., and Huang, T. S. (2009). Lin-

ear spatial pyramid matching using sparse coding for

image classiﬁcation. In CVPR.

Young, S., Evermann, G., Kershaw, D., Moore, G., Odell,

J., Ollason, D., Valtchev, V., and Woodland, P. (1995).

The HTK Book. Entropic Ltd., Cambridge, England.

Yu, K., Lin, Y., and Lafferty, J. (2011). Learning image

representations from the pixel level via hierarchical

sparse coding. In CVPR, pages 1713–1720.

BROADCAST NEWS PHONEME RECOGNITION BY SPARSE CODING

197