
SHAPE RECOGNITION USING THE LEAST SQUARES
APPROXIMATION
Nacéra Laiche and Slimane Larabi
Department of Computer, USTHB University, Algiers, Algeria
Keywords: Shape, Curvature Points, Approximation, Least-Squares method, Matching.
Abstract: This paper represents a novel algorithm to represent and recognize two dimensional curve based on its
convex hull and the Least-Squared modeling. It combines the advantages of the property of the convex hulls
that are particularly suitable for affine matching as they are affine invariant and the geometric properties of
a contour that make it more or less identifiable. The description scheme and the similarity measure
developed take into consideration technique for shape similarity. According to this method, the contours are
extracted and decomposed into portions of curves. Each portion curve is approximated by some explicit
curve using the Least Squares approximation. The obtained cubic curves are normalized in order to make
the method invariant to scale change. Finally the resulting curves are used to compare and to compute
similarity between shapes in images database using the Hausdorff distance. The proposed algorithm has
been tested and its performance is found favourable as compared to other matching techniques.
1 INTRODUCTION
Object representation and recognition is a very
difficult problem with many applications including
computer vision. Computer vision researchers aim to
capture image information in feature vectors which
describe shape, texture and color properties
databases of the image. These vectors are indexed or
compared to one another during query processing to
find similar images from the database. Considerable
amount of information exists in two dimensional
boundaries of objects since humans can readily
recognize an object using the shape of its boundary.
As a result, shape similarity retrieval plays an
important role in content based image database
systems.
Many techniques have been developed in the
literature to represent the shape of a free form 3D
object based on 2D silhouettes and most of them can
be classified into two categories: surface-based
methods and contour- based methods. Surface-based
methods extract features from the whole shape
region and are usually easy to compute and resistant
to noise and shape distortions. Different moments,
such as Zernike moments (Hwang et al., 2006)
(Chong et al., 2003) and Legendre moments (Yang
et al., 2006) have been demonstrated to achieve
excellent performance. These methods are not
suitable for object recognition in the presence of
occlusion. Unlike the contour-based methods
explore boundary shape information and are more
complicate requiring sophisticated implementations.
They are low, but more suitable than surface-based
methods for recognizing partially visible objects. In
this category we find: invariant features extracted
from boundaries of the object silhouette (Matusiak et
al, 1998), 2D boundary curves of silhouette using
Curvature Scale Space (CSS) (Mokhtarian et al.,
1992) and (Dudek et al., 1997). The polygonal
approximation has been used as a representation for
recognizing objects (Carmona-poyato et al., 2010).
Shape context (Belongie et al., 2002) is a method for
describing shapes and finding the correspondence
between point sets. Another shape descriptor is the
Medial Axis Transform, which was presented by
Blum (Blum, 1967) and later Sebastian and al
(Sebastian et al., 2004) used this descriptor for shape
recognition. Other techniques consist of approximate
the shape contour by Fourier descriptors (Zahn et al.,
1972) and B-spline (Paglieroni, 1985).
The notion of a part-based representation has
played an important role in object recognition. In
(Argawal et al, 2004), informative patches in the
images are derived from the training examples and
are used as fragments. Daliri and Torre (Daliri et al.,
2010) proposed a representation for shape-based
572
Laiche N. and Larabi S. (2012).
SHAPE RECOGNITION USING THE LEAST SQUARES APPROXIMATION.
In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 572-575
DOI: 10.5220/0003778405720575
Copyright
c
SciTePress
recognition based on the extraction of the
perceptually relevant fragments. Therefore, our aim
is to develop a recognition system which requires
two components: part-based representation and
matching method. The part-based silhouette
representation we use is built only on curves. Our
shape matching algorithm is done by introducing the
convex hull of the shape.
2 GEOMETRIC DESCRIPTION
Shape representation is one of the most challenging
aspects of computer vision because shapes are often
more complex than color and texture. The problem
remains difficult in similarity retrieval in image
databases. In This section, we present our approach
for representing shape by using Least Squares
approximation. The shape contour is first segmented
into several curve segments. Each curve segment is
then approximated by a cubic explicit curve using
the Least- Squares method.
2.1 Extracting the Local Boundary
Features (Parts)
In this section we describe how to extract the
different curve segments. The decomposition
process can be started by taking into account some
features of boundaries which exert a crucial role in
attracting the attention of an observer. Examples of
such features, closely related to those considered in
an early version of this paper are the high curvature
points which give important clues for shape
representation and analysis.
The basic step in our proposed algorithm is to
extract the curvature points using the Chetverikov
algorithm (Chetverikov, 2003) and locate the main
points that may preserve the object shape as concave
and convex points. Using the selected concave
points, the shape boundary is then decomposed into
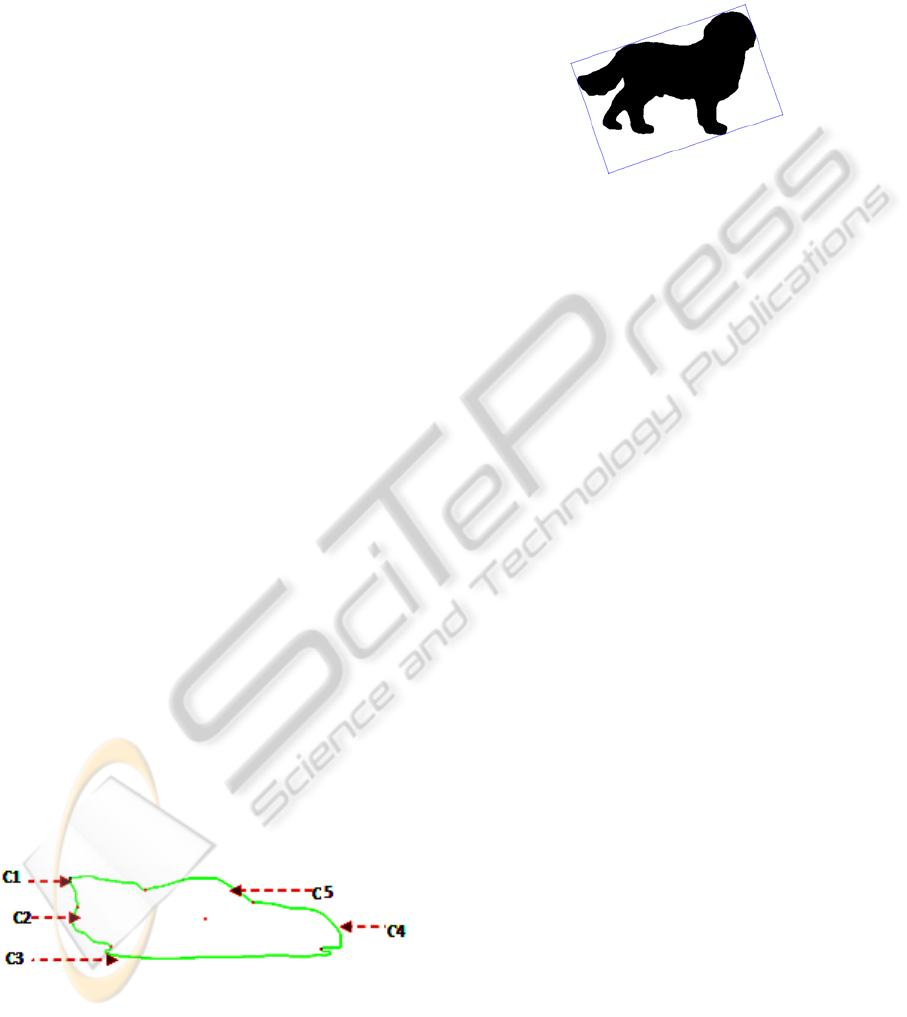
a set of portions of curves as illustrated in Fig. 1.
Figure 1: Shape with different parts.
2.2 Curves Modelling
Our approach consists first in the use of the
minimum rectangle MR that encloses the outline
shape (Graham, 1972). OXY is the referential
attached to MR chosen such as the origin O is the
left top edge of MR and the OX (resp. OY) axis
corresponds to the width (resp. length) of the outline
shape (see Fig. 2).
Figure 2: The minimum rectangle MR including the shape.
Given a shape contour
Ω
. We assume that the
original contour
Ω
is close, Ω is traversed in a
counter-clockwise sense (the object is to the left).
Ω
Consists of a finite number of an ordered list of
parts that define the shape of the object silhouette
(see Fig. 1). A curve modelling should be applied in
order to facilitate matching and recognizing object
shapes. In this paper the Least Squares model is
employed to approximate each cut (part)
i
C by an
explicit cubic curve. The least squares curve of order
3 is defined by
3
23
01 2 3
0
()
j
ij
j
Cx ax a ax ax ax
=
==+++
∑
(1)
Where the polynomial factors
)
3,2,1,0=i
i
a are
computed such that the sum of the quadratic errors
between the discrete data and their corresponding
least squares curve is minimized.
2.2.1 Normalization
In this subsection, we introduce the convex hull of
the shape to generate an invariant representation.
Convex hulls have some properties that make them
suitable for recognition and representation tasks
(Preparata et al., 1985).
The boundary
Ω
of any object consists of a
finite number of an ordered sequence of points that
define the shape of an object:
{
}
n
ppp ,.......,,
21
=
Ω
consisting of n two-
dimensional points. Let
H
C denotes the convex hull
for the set
Ω
. Let
(
)
ii
yx , ,
mi ,.....,2,1=
be the
ordered vertices forming the convex hull. Using the
Green’s theorem (Gope et al., 2007) the centroid of
H
C denoted by
),(
yxg
ccC
=
can be expressed as:
SHAPE RECOGNITION USING THE LEAST SQUARES APPROXIMATION
573

()( )
()( )
1
111
1
1
111
1
1
6
1
6
m
x
ii ii ii
i
m
y
ii ii ii
i
cxxxyxy
A
cyyxyxy
A
−
+++
=
−
+++
=
⎧
=+ −
⎪
⎪
⎨
⎪
=+ −
⎪
⎩
∑
∑
(2)
Where
A
is the area of
H
C given by
()
1
11
1
1
2
m
ii i i
i
Axyxy
−
++
=
=−
∑
(3)
In order to make the representation invariant to scale
change we carry out a transformation on the
approximation points. This can be accomplished by
converting each approximation point
)','(
ii
yx of
each curve to another point by the transformation:
'
'
'
'
i
i
M
ax
i
i
M
ax
x
x
d
y
y
d
⎧
→
⎪
⎪
⎨
⎪
→
⎪
⎩
(4)
Where
{
}
),(max
igMax
pCdd =
represents the
maximal distance from the centroid of the convex
hull of the shape to the boundary curve.
This transformation allows us to bring back the
different cubic curves approximating the original
boundary curve at the different sizes on the same
neighborhood
3 SHAPE MATCHING
In this section, we describe the basic concepts of our
matching algorithm which compares images of the
database with a query image. Consider that the
features here are related to the convex hull and the
normalized curves.
3.1 Boundary Signature Matching
The boundary signature
γ
extracted from an object’s
boundary that characterizes the shape of an object is
defined as the ratio of the minimal Euclidean
distance between the centroid of the convex hull and
the boundary shape to the maximal Euclidean
distance
Max
d . Matching between query shape to
models is accomplished by comparing their
boundary signatures.
3.2 Computing Shape Similarity
A necessary condition to match two shapes (query
and model shapes) is the similarity between of their
all normalized curves.
3.2.1 Matching using the Normalized
Curves
In this section, we explain how to match two curves.
Hausdorff distance is used for matching two
different curves.
Given two normalized curves C
and
'C of a query shape
Q
and a reference shape
M
respectively, the Hausdorff distance is defined
as:
( , ') max( ( , '), ( ', ))HCC hCC hC C
=
(5)
Where
''
(, ') maxmin '
cC
cC
hCC c c
∈
∈
=
−
(6)
and
. is a norm defined on the curve, such as the
2
L
norm.
A valid match between two normalized curves is
found if the maximal difference between them (the
similarity measure defined above) is under a
threshold defined experimentally
C
E ; otherwise
they are different.
4 EXPERIMENTAL RESULTS
Our method is tested on ETH-80 database of 80
objects built by Leibe and B.Schiele (Leibe et al.,
2003). Each object is represented by some views
spaced evenly over the upper viewing hemisphere.
The method possesses the important property of
rotation and scale change. Invariance to rotation is
achieved by computing using the referential defined
by the minimum rectangle that encloses the shape.
Using the maximal distance from the centroid of the
convex hull, the representation is invariant to scale
change. Some of the matching results are shown in
Figure 3. The queries shapes are in the first row (at
the left of each row). The similar shapes that have
been matched by the proposed algorithm are shown
in the rest rows. In the examples shown in Figure 3
there is a difference in the view angle between the
query shape and the similar shapes. This examples
show the robustness of our approach to orientation
changes of the shapes.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
574

Figure 3: More matching of results.
We have summarized recognition rates for some
different approaches which are tested on the ETH-80
database and cited in (Daliri et al., 2009).
Table 1: Some recognition rates for different algorithms
tested on ETH-80 database.
Algorithm Recognition rate (%)
SC greedy 86.40
Decision tree 93.02
Fragment-based
approach
86.40
Kernel-edit-distance 91.33
Robust symbolic
representation
89.03
Proposed algorithm 92.50
5 CONCLUSIONS
In this paper, we have presented a new approach to
represent the shape of the projection of a 3D object
which enables similarity search. A key characteristic
of our approach is the use of the geometric
description of different parts constituting the outer
closed boundary of the shape using a set of cubic
curves. These curves enable us comparisons between
different shapes. A shape matching technique, using
the Hausdorff distance between two curves has been
proposed. In our experiments, we have demonstrated
invariance to similarity transformations: rotation and
scaling. The results are encouraging. The proposed
approach achieves a recognition rate equal to 92.5%.
REFERENCES
Argawal, S., Awan, A., Roth, D., 2004. Learning to detect
objects in images via a sparse Part-base representation.
In IEEE TPAMI. 26 (11), 1475-1490.
Belongie, S., Malik, J., Puzicha, J., 2002. Shape matching
and object recognition using shape contexts. In IEEE
TRANS. PAMI 24 (24), 509-521.
Blum, H., 1967. A transformation for extracting new
descriptors of shape. In Models for the perception of
speech and visual form. MITPress, 362-379.
Carmona-poyato, A., Madrid-Cuevas, F. J., Medina-
Carnicer, R., Munoz-Salinas, R., 2010. Polygonal
approximation of digital planar curves through break
point suppression. In: Pattern Recognition 43, 14-25.
Chetvericov, D., 2003. A Simple and efficient algorithm
for detection of high curvature points in planar curves.
In 10
th
International Conference. CAIP, 25-27.
Chong, C. W., Raveendran, P., Mukundan, R., 2003.
Translation invariants of Zernike moments. In: Pattern
Recognition. 1765-1773.
Daliri, M. R., Torre, V., 2010. Classification of silhouettes
using contour fragments. In Computer Vision and
Image Understanding. 113, 1017-1025.
Dudek, G., Tsotsos, J. K., 1997. Shape representation and
recognition from multiscale curvature. In: Computer.
Vision and Image Understanding. 68, N2, 170-187.
Gope, C., Kehtarnavaz, N., 2007. Affine invariant
comparison of point-sets using convex hulls and
Hausdorff distances. In Pattern Recognition. 40, 309-
320.
Graham, R. L., 1972. An efficient algorithm for
determining the convex hull of a finite planar set. In
Information Processing Letters.
Hwang, S. K., Kim, W. Y., 2006. A novel approach to the
fast computation of Zernike moments. In: Pattern
Recognition. 39, 2065-2076.
Leibe, B., Scheille, B., 2003. Analysing appearance and
contour based methods for object categorization. In
International Conference on Computer Vision and
Pattern Recognition. Madison,Wisconsin.
Matusiak, S., Daoudi, M., Ghorbel, F., 1998. Planar closed
contour representation by invariant under a general
affine transformation. In IEEE International
Conference on Systems, Man, and Cybernetic.
Mokhtarian, F., Makworth, A. K., 1992. A theory of
multiscale curvature-based shape representation of
planar curves. In: IEEE Transactions on Pattern
Analysis and Machine Intelligence. 789-809.
Preparata, F., Shamos, M., 1985. Computational
Geometry: An introduction, Springer, Berlin,
Germany.
Sebastian, T. B., Klein, P. N., Kimia, B. B., 2004.
Recognition of shapes by editing their shock graphs.
In IEEE TRANS. PAMI 26 (5), 550-571.
Yang, G. Y., Shu, H. Z., Toumoulin, C., Han, G. N., Luo,
L. M., 2006. Efficient Legendre moments computation
for grey level images. In: Pattern Recognition. 39, 74-
80.
Zahn, C., Roskies, R., 1972. Fourier descriptors for plane
closed curves. In IEEE TRANS.Computers.269-281.
SHAPE RECOGNITION USING THE LEAST SQUARES APPROXIMATION
575
