EFFICIENT PATH KERNELS FOR REACTION FUNCTION

PREDICTION

Markus Heinonen

∗

, Niko V

alim

aki

∗

, Veli M

akinen and Juho Rousu

Department of Computer Science, University of Helsinki, Helsinki, Finland

Keywords:

Graph kernels, Compressed data structures, XBW transform, Reaction graph, Hierarchical classiﬁcation.

Abstract:

Kernels for structured data are rapidly becoming an essential part of the machine learning toolbox. Graph

kernels provide similarity measures for complex relational objects, such as molecules and enzymes. Graph

kernels based on walks are popular due their fast computation but their predictive performance is often not

satisfactory, while kernels based on subgraphs suffer from high computational cost and are limited to small

substructures. Kernels based on paths offer a promising middle ground between these two extremes. However,

the computation of path kernels has so far been assumed computationally too challenging. In this paper we

introduce an effective method for computing path based kernels; we employ a Burrows-Wheeler transform

based compressed path index for fast and space-efﬁcient enumeration of paths. Unlike many kernel algorithms

the index representation retains fast access to individual features. In our experiments with chemical reaction

graphs, path based kernels surpass state-of-the-art graph kernels in prediction accuracy.

1 INTRODUCTION

Kernel methods have proven an efﬁcient approach in

machine learning tasks, such as classiﬁcation, regres-

sion and clustering (Shawe-Taylor and Christianini,

2004). A kernel deﬁnes a similarity function between

two objects, which corresponds to implicitly mapping

the objects to a feature space, in which a dot product

equals the kernel value. This property of kernels is

especially suitable for complex structural data, as the

object’s vectorial representation is formed automati-

cally.

Graph kernels try to capture the essential topo-

logical features of the graph by providing a (possi-

bly inﬁnite) feature vector representation of the graph,

and subsequently computing the similarity between

the feature vectors. Paired with kernel methods, the

relevant application-dependent substructure signals

can be exploited. Graph kernels can be categorised

based on the generality of the feature class: sequence

based kernels enumerate e.g. walks or paths, subtree

based kernels allow sequences to branch, and sub-

graph based kernels place no restrictions on the sub-

structure.

The commonly used walk kernels can be com-

puted efﬁciently up to inﬁnite length, but they contain

∗

Equal contribution from these authors

arbitrary repeats of themselves (G

artner, 2003). Any

walk can continue inﬁnitely by traversing itself back

and forth. These repeated walks contain no additional

information about the graph, however they result in

inﬁnite feature space and in kernels with large norms.

Down weighting longer walks alleviates the problem

artner, 2003). In (Mahe et al., 2005) the problem

was fought by introducing non-tottering walks, where

tottering cycles of length two are prohibited in walks.

Kernels based on paths, that is walks with no rep-

etitions, are more challenging to compute and few

practical algorithms so far exists. In (Borgwardt et al.,

2005) an efﬁcient kernel using shortest paths between

nodes in the graphs was proposed. The shortest paths

kernel has an exceptionally small feature space as

there only exists n

shortest paths in a graph of size

n, which makes its efﬁcient to compute. In (Ralaivola

et al., 2005) a sufﬁx trees was utilized in computing

the pairwise path kernels individually up to length 10.

However, so far a method for efﬁciently computing

an all-paths kernel has been missing. In this paper we

propose an efﬁcient method for computing path ker-

nels using a compressed path index as an intermediate

data structure. The compressed path index is based on

a Burrows-Wheeler transform of labeled trees (Fer-

ragina et al., 2009) and contains the feature values ex-

plicitly which allows for various kernel functions in

the feature space.

202

Heinonen M., Välimäki N., Mäkinen V. and Rousu J..

EFFICIENT PATH KERNELS FOR REACTION FUNCTION PREDICTION.

DOI: 10.5220/0003779402020207

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2012), pages 202-207

ISBN: 978-989-8425-90-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

We take two steps to compute path kernels when

given a set of graphs as an input: First, we create a

specialized path index that represents all the paths,

up to some maximum length, of all graphs in com-

pressed form and allows us to efﬁciently traverse all

unique paths and output their frequencies for desired

graphs. Then, the path frequencies are used to com-

pute path kernels via inner products. In our experi-

ments we compare path based graph kernels against

walk based kernels, shortest paths based kernels, as

well as the custom reaction graph kernel by (Saigo

et al., 2010). The performance is evaluated in a hi-

erachical multilabel classiﬁcation task of assigning a

biochemical reaction to the correct branch of the En-

zyme Commision (EC) hierarchy.

In section 2 we review existing sequence based

kernels on graphs, including the shortest paths kernel.

In section 3 the compressed path index for the com-

putation of path kernels is introduced. In section 4

experiments are carried out where the path based ker-

nels are compared against state-of-the-art graph ker-

nels. We also review the run time performance of our

method. We conclude with discussions in section 5.

2 GRAPH KERNELS

In this section we review existing approaches for com-

puting graph kernels. We consider a labeled undi-

rected graph G = (V, E,L) with n nodes, where a la-

beling function L applies to both nodes v ∈ V and

edges (v,u) ∈ E. A walk w is a sequence of adjacent

vertices. A path p is a walk where no node repeats.

Random walk kernels compute the weighted sum

of matching walks in a pair of graphs, utilizing either

the adjacency matrix exponential (G

artner, 2003) or

a markov process model (Kashima et al., 2003). If

the contribution of each walk is downscaled appropri-

ately according to its length k with λ

the walk kernel

can be computed until convergence in cubic time. An

generalization to marginalized kernels prevents non-

tottering walks by utilizing second order markov pro-

cesses (Mahe et al., 2005).

With λ < 1 the contribution of longer walks

quickly becomes negligible and long walks have ef-

fectively no effect on the kernel value in the stan-

dard walk kernel. This is sometimes against what

we desire – longer walks may contain important in-

formation for e.g. graphs with repetitive substruc-

tures, where the walk length is required to surpass

the diameter of the substructure to notice the repeti-

tion. Therefore we consider ﬁnite-length walk ker-

nels, where walks up to length k are constructed ex-

plicitly. Working with explicit walks allows us to re-

gard paths and non-tottering walks. We can count the

number of matching k-length walks in two graphs by

using dynamic programming (Demco, 2009).

Borgwardt et al. deﬁned a family of kernels

using special subsets of paths, namely the set

of shortest paths between all nodes (Borgwardt

et al., 2005). All pair shortest paths can be

computed with Floyd-Warshall algorithm in O(n

)

time. The kernel is then deﬁned K

(G,G

) =

∑

p∈S P (G),p

∈S P (G

)

(p, p

), where S P (G) is the set

of shortest paths between all nodes of graph G and K

is a positive semi-deﬁnite path matching kernel. How-

ever, in many applications it is not clear that shortest

paths carry a special meaning. Thus efﬁcient methods

to compute path kernels with a broader feature space

is still desirable.

3 COMPUTING PATH KERNELS

VIA COMPRESSED PATH

INDEX

We wish to use the set of all paths to characterize a

given graph. We deﬁne an all paths kernel as a dot

product between shared path counts. Computing the

path kernel is known to be NP-hard (Borgwardt et al.,

2005). However, we will show here that it is possible

to compute them with typical molecular datasets such

as KEGG reaction database.

We use a four-fold procedure to compute the ker-

nel. First, trees up to height h of all graphs are enu-

merated using each node subsequently as the root

node. Then, the resulting trees are used as an input to

a path index construction. Finally, the feature values

are extracted from the index, and the kernel is explic-

itly computed.

Path Enumeration. For each vertex u ∈ V , we

build a tree T

that contains all paths originating from

u. This can be done with a depth-ﬁrst traversal in G,

and the result is a set of trees T = {T

| u ∈ V }. Fig-

ure 1 gives an example of a graph and one of the trees

generated. When multiple graphs G

,.. .,G

are

given, each graph can be processed separately cre-

ating a set of tree sets T

,.. .,T

. Path enumera-

tion can be generalized to directed and edge-labeled

graphs.

Path Index Construction. We store the set of trees

as a path-sorted transform dubbed XBWT (Ferragina

et al., 2009). We will show how the resulting index

can be used to efﬁciently compute path frequencies,

EFFICIENT PATH KERNELS FOR REACTION FUNCTION PREDICTION

203

A B

(a)

b c

(b)

last

0 A empty

0 B A

1 C A

1 B BA

0 b BA

1 c BA

1 c BBA

1 b BCA

1 B CA

(c)

Figure 1: (a) Example graph. (b) Paths originating from

node A. (c) An XBWT representation of the tree in (b).

The rows are lexicographically sorted by upward paths, S

which are displayed here for reference and not stored at any

point of the algorithm.

but ﬁrst, let us describe how to construct the transform

for a single tree T of t nodes.

The XBWT of T is constructed in two phases

(Ferragina et al., 2009). The ﬁrst phase starts by ini-

tializing an array S[1,t] to contain the nodes in pre-

order: for each node u, we store its label α[u], a parent

pointer and a boolean value last[u]. We set last[u] = 1

if u is the right-most child of its parent. Finally, we

need to be able to distinguish between internal and

leaf node labels — for example, in Figure 1, we use

lower-case labels for leaves. In the second phase, S

is stably sorted according to the lexicographical order

of node’s upward path π[u], that is, the labeled path

from u to the root. In (Ferragina et al., 2009) an op-

timal O(t)-time algorithm was given to sort S in im-

plicit manner, without a need to store the π[u] values

explicitly.

The ﬁnal XBWT of T consists of a bitvector S

last

and an array of node labels, denoted by S

. They are

populated simply by following the order the nodes ap-

pear in S after the sorting phase. Figure 1(c) gives an

example of values of S

and S

last

for the tree in Fig-

ure 1(b). The actual index, which grants us naviga-

tional operations on T and efﬁcient way of counting

path frequencies, requires rank and select queries on

and S

last

. The query rank

,i) gives the number

of times c appears in S

[1,i], and select

,i) gives

the position of the i-th c in S

. Both of these queries

can be solved in O(logσ/log logt) time, for any al-

phabet size σ = O(t

) and ε < 1, by using a Wavelet

tree data structure requiring tH

) + o(t log σ) bits

of memory (Ferragina et al., 2007), where H

) ≤

logσ is the 0-th order entropy of S

Thus, the whole

index requires in total tH

)+t + o(t) bits, plus an-

other t bits if we use an additional bitvector to dis-

tinguish leaf node labels. The XBWT representation

Algorithm traverse(s,e,P,l f ):

1 C ← Set of internal node symbols on S

[s,e].

2 L ← Set of leaf node symbols appearing on S

[s,e].

3 for each c ∈ C do

4 l f

← 0

5 if leaf(c) ∈ L then

6 L ← L \ leaf(c)

7 l f

← Number of leaf(c) in S

[s,e].

8 z

← select

,rank

,s − 1) + 1)

9 z

← select

,rank

,e))

10 s

← GetRankedChild(z

,1)

11 e

← GetRankedChild(z

,GetDegree(z

))

12 traverse(s

,cP, l f

)

13 for each c ∈ L do

14 l f

← Number of leaf symbols c in S

[s,e].

15 Output subpath cP with frequency l f

16 f ← rank

last

,e) − rank

last

,s − 1)

17 Output subpath P with frequency f + l f .

Figure 2: Recursive algorithm to traverse through all

uniquely labeled, root-originating paths. The ﬁrst call of

the recursion is traverse(1, 1, empty,0). Function leaf(c)

is just a simple conversion between internal and leaf node

labels, e.g. an upper-case conversion in Figure 1.

generalizes to multiple trees quite naturally — we

omit the technical details here for brevity.

In (Ferragina et al., 2009) a comprehensive list of

navigational operations supported by the index were

introduced. Due to the lexicographical ordering of

S, all children of an internal node occur at a speciﬁc

range [s,e] in S. For example, children of the root

node in Figure 1(c) can be found on rows [2,4]. Oper-

ation GetChild(i) returns the range [s,e] correspond-

ing to all the children of S[i] in O(log σ/ log log n)

time (we omit details here for brevity) (Ferragina

et al., 2009). Similarly, GetRankedChild(i, j) returns

the j-th child of i, which is simply s + j − 1. The de-

gree of node i is GetDegree(i) = e − s +1 where [s,e]

is given by GetChild(i).

Computing Path Frequencies. Next we will give

a recursive algorithm to output, for all unique root-

originating paths, the number of times the path oc-

curs, i.e. path’s frequency, in each tree. For now, as-

sume that we are given an index containing one tree T .

At the start of the recursion, we initialize the current

subpath P to be empty, and set s = e = 1. The follow-

ing invariant holds throughout the recursion: at every

step, the range S[s,e] corresponds to all nodes having

upward path equal to P.

Each recursion step proceeds as follows. First we

enumerate all unique labels appearing on the range

[s,e] by using a range search on the Wavelet tree

(cf. rows 1–2 in Figure 2). The labels can branch ei-

ther to internal nodes or leaf nodes, or both. For each

label c that branches with internal nodes, we locate

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

204

the ﬁrst and last occurrence of c in S

[s,e] (rows 8–

9) and take their ﬁrst and last child as the new range

(rows 10-11). Then a recursive call is done for the

new range [s

] and subpath P

= cP. However, if

there are also leaf nodes branching with c, their fre-

quencies must be passed on for the recursive call since

leaves that match the path cP appear on S[s,e] in-

stead of the new interval (rows 5–7). Furthermore,

remaining leaf symbols must be handled separately

(rows 13–15). Finally, we output the frequency of the

current subpath P, which equals the number of 1-bits

in S

last

[s,e] plus the leaf frequency passed on down-

wards in recursion (rows 16–17).

Let us give a short example using Figure 1(c). As-

sume that we arrive at the range [5,7] which corre-

sponds to subpath P = BA. We branch with B which

gives us the new range [8,8]. However, there is also a

leaf branching with B in the range [5,7] (and recall

that we use lower-case to distinguish leaves), thus,

when we recursively call for the new range [8,8], we

also pass on the information about the branching leaf.

Final frequency of P

= BBA is then 2.

The time complexity of each recursion step is

dominated by the range search on the Wavelet tree

(rows 1–2), which requires (with a naive approach)

time proportional to the length of the interval, i.e.

O((e − s + 1)log σ). Since the recursion iterates only

over root-originating paths, the intervals [s,e] are all

non-overlapping. Thus, the total time complexity

is O(t log σ). Moreover, we can generalize the fre-

quency counting for a set of trees or multiple tree sets

while retaining the same time complexity.

Computing the Kernel. We use a Dirac kernel to

compare individual paths. The kernel is computed di-

rectly as a dot product between path feature vectors.

4 EXPERIMENTS

In this section, we evaluate the performance of path

kernels against state-of-the-art graph kernels in a pre-

diction task from (Saigo et al., 2010), where the EC

number of a reaction is predicted. An EC code anno-

tates the function of an enzymatic reaction in a four-

level hierarchical numeric code “a.b.c.d”, where the

ﬁrst level indicates the general class of the enzyme

(ligases, lyases, isomerases, etc.) and following lev-

els specify the reaction mechanisms. The fourth level

is arbitrary index and ignored. Thus there are 270 full

EC codes.

Reaction Dataset. We perform the experiments

on a reaction set from KEGG LIGAND database

representing common metabolic reactions (release

1.7.2010). A chemical reaction is a graph transforma-

tion, where substrates are transformed into products

often catalyzed by an enzyme, which rearranges the

bonds of the chemical compounds. We constructed

graph representations of the reactions by modeling

the substrates and products as two separate disjoint

graphs with a bi-partite optimal atom mapping be-

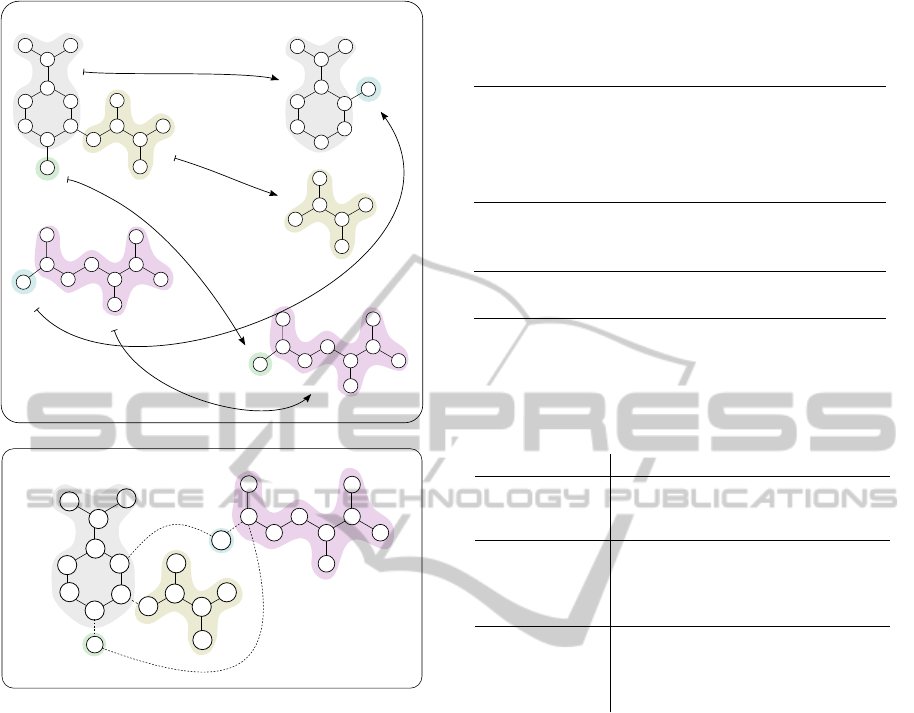
tween the two graphs’ nodes (see top of Figure 3)

(Heinonen et al., 2011). A reaction graph is con-

structed by rerouting edges of the product side to

the substrate side through the mapping, and removing

product nodes (see bottom of Figure 3) (Felix et al.,

2005).

The dataset consists of 15566 EC-labeled reac-

tion graphs computed using optimal atom mappings.

All reactions are theoretically capable of functioning

in forward and backward directions, thus we include

both versions by constructing a direction-invariant

tensor kernel as in (Astikainen et al., 2011) resulting

in 7783 reactions. Median size of reaction graphs is

38 and maximum 393.

Kernels for Reactions. We compare our path ker-

nels to the simple walk kernel (up to length k = 15),

shortest path kernel, and the RGK kernel by (Saigo

et al., 2010), speciﬁcally introduced for reactions. In

RGK an alternative reaction graph model is deﬁned,

which uses inner and outer marginal walk kernels to

compare similarity of reactions.

The path index was implemented by reusing our

own existing C/C++ implementations of Huffman-

shaped Wavelet trees (Grossi et al., 2004) and bitvec-

tors supporting rank and select queries (Jacobson,

1989). Optimal construction time and space are not

yet achieved since our current implementation of the

sorting phase requires O(t log

t) time and Θ(t logt)

bits of memory. We are currently planning to improve

the sorting phase by plugging in a more sophisticated

path sorting method (Ferragina et al., 2009). Table 1

gives a summary of the performance of the path index.

We ran the experiments with MMCRF hierarchi-

cal multilabel classiﬁcation algorithm (Rousu et al.,

2007). All kernels use λ = 0.90 and non-RGK ker-

nels are tensor kernels. A 5-fold cross-validation pro-

cedure was used and an optimal C-parameter was cho-

sen from {1,10, 100,1000,10000}. We employ nor-

malized quadratic kernels as they achieved consis-

tently best results.

Results. The results are shown in table 2. A reac-

tion mechanism is deemed correctly classiﬁed if the

correct root-to-leaf branch of the EC hierachy is pre-

dicted by MMCRF. The walk kernel is clearly infe-

EFFICIENT PATH KERNELS FOR REACTION FUNCTION PREDICTION

205

O O

C C

new

removed

Pyruvate

Anthranilate

Glutamate

Chorismate

Glutamine

Figure 3: Reaction R00986: Chorismate pyruvate-

lyase in forward direction and its optimal atom mapping

(top). Atom mapping is highlighted with corresponding col-

ors and the corresponding reaction graph is below. The “+1”

edges are marked as new and “-1” edges are removed.

rior to the other kernels in this test. RGK and shortest

paths kernels fared better achieving a test set error of

35.0% and 36.4%, respectively. Variants of the path

kernels achieved a minimum of 24.3% test error.

We experimented with upper bounds 15 and 50 for

path length. The results are similar or slightly better

for the upper bound 15, indicating that most informa-

tion resides in shorter paths. However the overﬁtting

effect of the signiﬁcantly larger feature space associ-

ated with the bound 50 is relatively small.

With compressed path index it is trivial to pick a

subset of paths to focus on. We experimented with

core paths, paths that go through modiﬁed edges (la-

beled “+1” or “-1”). These paths are most likely most

relevant regarding the reaction transformation. The

results show that using core paths decreases the error

to 28.9% from 34.2% of the all path version. How-

ever, when using indicator feature values (all features

are binary) the all-path kernel achieves the lowest er-

Table 1: Characteristics of the test data and performance

results. Note that both construction time and space can still

be optimized with a small engineering effort. Experiments

run on Xeon X7350 CPU and 128 GB of memory.

# of reaction graphs 17,430

# of trees 746,438

# of tree nodes 279 mil.

# of tree leaves 91 mil.

max. tree depth 50

Index construction time 1.1 hours

Index construction space 4.4 GB

Final index size 1.1 GB

# of unique paths 21 mil.

Index frequency computation 176 s

Kernel computation (path length 50) 718 s

MMCRF run (average, 5-fold cv) 10 hours

Table 2: Prediction of full EC class. Core path kernel only

includes paths with “+1” or “-1” edges, while indicator ker-

nels contain only binary values.

Kernel k Tr. error (%) Ts. error (%)

Walk 15 52.9 61.1

RGK inf 27.8 35.0

Shortest paths 21.5 36.4

Core paths 50 14.9 28.9

Core paths, ind 50 14.5 27.8

All paths 50 19.6 34.2

All paths, ind 50 9.1 25.6

Core paths 15 15.0 28.3

Core paths, ind 15 14.7 27.3

All paths 15 20.0 33.7

All paths, ind 15 9.2 24.3

ror rates independent of the upper bound on the path

length. It seems that core paths provides a clearer sig-

nal to the learning machine, but using indicators for

all paths achieves an even stronger effect.

An experiment with the max kernel had a small

less than 1% positive effect on accuracies (data not

shown). The max kernel is not positive semi-deﬁnite,

although the smallest negative eigenvalue is relatively

small. The MMCRF seemed to converge in spite of

the indeﬁnite setting. The values on Table 2 are from

the max kernel.

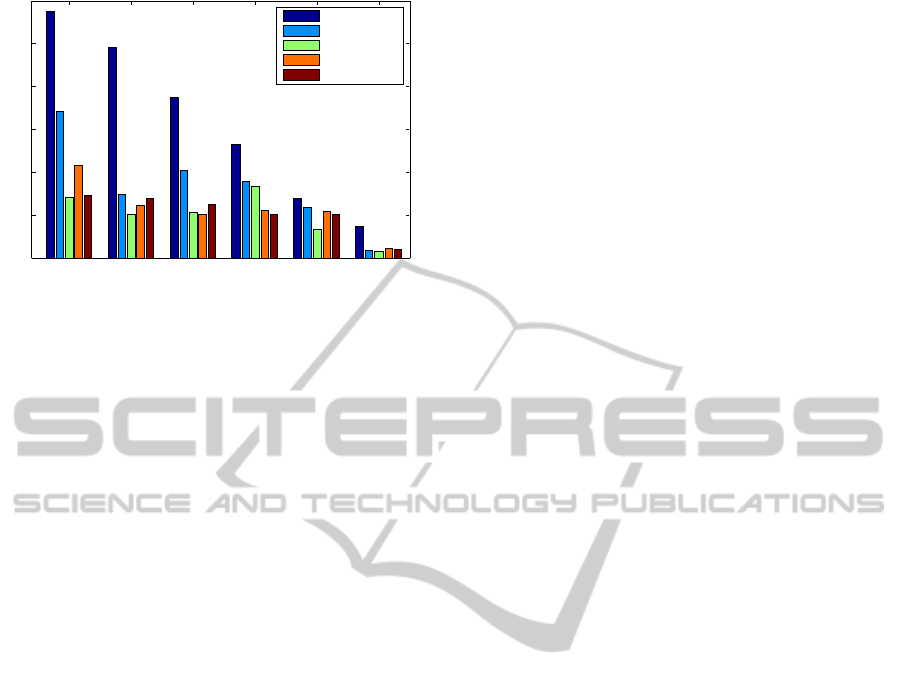
Figure 4 shows the performance of ﬁve main ker-

nels on the EC main class only. The main classes are

most general and are thus most difﬁcult to predict.

Here, RGK kernel is on par with path kernels. The

ﬁrst EC class of oxidoreductases is most difﬁcult to

predict. The high performance on the sixth class of

ligases can be explained by the homogeneity of the

ligases.

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

206

EC1 EC2 EC3 EC4 EC5 EC6

2.5

7.5

12.5

EC Class

Test error (%)

Walks

Shortest paths

RGK

Core paths

All paths

Figure 4: Prediction results for the six main EC classes. The

ﬁrst EC class (oxidoreductases) is most difﬁcult, while the

last (ligases) is well predicted with any method.

5 DISCUSSION AND

CONCLUSIONS

The path index can also be used for on-line path fre-

quency queries: given any path P of length m ≤ h,

where h is the maximum path length enumerated, we

can output the frequency of the path P in all graphs

in just O(m log σ + output) time, where output is the

size of the output, i.e. the number of distinct graphs

having frequency that is greater than zero. Details are

out of the scope of this paper, but this type of on-line

feature query might be interesting when computing

kernels in iterative manner. Another interesting di-

rection would be to implement feature selection or `

regularized learning methods for graph data making

use of the efﬁcient access to features.

We presented a method for efﬁciently computing

all-paths kernels for graph data. Our approach relies

on computing and storing a single compressed path

index of all graphs, which can subsequently be efﬁ-

ciently queried for the purposes for graph kernel or

feature vector computation. We demonstrate the com-

putational feasibility of the approach by computing a

path index for graph representations of KEGG reac-

tions. Our experiments show that path kernels give

signiﬁcant improvements over walk kernels in the re-

action mechanism prediction task.

ACKNOWLEDGEMENTS

We are grateful to Petteri Kaski, Mikko Koivisto

and Craig Saunders for insightful discussions. This

work was funded by the Academy of Finland grants

1140727 and 118653, the Graduate School Hecse and

by the PASCAL2 (IST grant-2007-216886).

REFERENCES

Astikainen, K., Holm, L., Pitk

anen, E., Szedmak, S., and

Rousu, J. (2011). Structured output prediction of

novel enzyme function with reaction kernels. In

Biomedical Engineering Systems and Technologies,

pages 367–378. Springer.

Borgwardt, K., Ong, C., Sch

onauer, S., Vishwanathan, S.,

Smola, A., and Kriegel, H.-P. (2005). Protein function

prediction via graph kernels. Bioinformatics, 21:i47.

Demco, A. (2009). Graph Kernel Extension and Exper-

iments with Application to Molecule Classiﬁcation,

Lead Hopping and Multiple Targets. PhD thesis, Uni-

versity of Southampton.

Felix, H., Rossello, F., and Valiente, G. (2005). Optimal

artiﬁcial chemistries and metabolic pathways. In Proc.

6th Mexican Int. Conf. Computer Science, pages 298–

305. IEEE Computer Science Press.

Ferragina, P., Luccio, F., Manzini, G., and Muthukrishnan,

S. (2009). Compressing and indexing labeled trees,

with applications. J. ACM, 57:4:1–4:33.

Ferragina, P., Manzini, G., M

akinen, V., and Navarro, G.

(2007). Compressed representations of sequences and

full-text indexes. ACM Transactions on Algorithms

(TALG), 3(2):article 20.

artner, T. (2003). A survey of kernels for structured data.

ACM SIGKDD Explorations Newsletter, 5:49–58.

Grossi, R., Gupta, A., and Vitter, J. S. (2004). When index-

ing equals compression: experiments with compress-

ing sufﬁx arrays and applications. In Proc. 15th an-

nual ACM-SIAM Symposium on Discrete Algorithms,

pages 636–645, Philadelphia, PA, USA. SIAM.

Heinonen, M., Lappalainen, S., Mielik

ainen, T., and Rousu,

J. (2011). Computing atom mappings for biochemical

reactions without subgraph isomorphism. J. Comp.

Biology, 18:43–58.

Jacobson, G. (1989). Succinct Static Data Structures. PhD

thesis, Carnegie–Mellon. CMU-CS-89-112.

Kashima, H., Tsuda, K., and Inokuchi, A. (2003). Marginal-

ized kernels between labeled graphs. In Proc. 20th Int.

Conf. on Machine Learning (ICML), pages 321–328.

Mahe, P., Ueda, N., Akutsu, T., Perret, J.-L., and Vert, J.-P.

(2005). Graph kernels for molecular structure-activity

relationship analysis with support vector machines. J.

Chem. Inf. Model., 45:939–951.

Ralaivola, L., Swamidass, S., Saigo, H., and Baldi, P.

(2005). Graph kernels for chemical informatics. Neu-

ral Networks, 18:1093–1110.

Rousu, J., Saunders, C., Szedmak, S., and Shawe-Taylor,

J. (2007). Efﬁcient algorithms for max-margin struc-

tured classiﬁcation. Predicting Structured Data, pages

105–129.

Saigo, H., Hattori, M., Kashima, H., and Tsuda, K.

(2010). Reaction graph kernels predict ec numbers

of unknown enzymatic reactions in plant secondary

metabolism. BMC Bioinformatics, 11:S31.

Shawe-Taylor, J. and Christianini, N. (2004). Kernel Meth-

ods for Pattern Analysis. Cambridge University Press.

EFFICIENT PATH KERNELS FOR REACTION FUNCTION PREDICTION

207