
IMPACT OF WINDOW LENGTH AND DECORRELATION STEP ON
ICA ALGORITHMS FOR EEG BLIND SOURCE SEPARATION
Gundars Korats
1,2
, Steven Le Cam
1
and Radu Ranta
1
1
CRAN UMR 7039 Nancy Université, CNRS, 2 Avenue de la Forêt de Haye, 54516, Vandoeuvre-les-Nancy, France
2
Ventspils University College, 101 Inzenieru iela, LV-3601, Ventspils, Latvia
Keywords:
EEG, BSS, ICA, Whitening, Sphering.
Abstract:
Blind Source Separation (BSS) approaches for multi-channel EEG processing are popular, and in particular
Independant Component Analysis (ICA) algorithms have proven their ability for artifacts removal and source
extraction for this very specific class of signals. However, the blind aspect of these techniques implies well-
known drawbacks. As these methods are based on estimated statistics from the data and rely on an hypothesis
of signal stationarity, the length of the window is crucial and has to be chosen carefully: large enough to get
reliable estimation and short enough to respect the rather non-stationary nature of the EEG signals. In addition,
another issue concerns the plausibility of the resulting separated sources. Indeed, some authors suggested
that ICA algorithms give more physiologically plausible results depending on the chosen whitening/sphering
step. In this paper, we address both issues by comparing three popular ICA algorithms (namely FastICA,
Extended InfoMax and JADER) on EEG-like simulated data and assessing their performance by using an
original correlation matrices distance measure and a separation performance index. The results are consistent
and lead us to a precise idea of minimal sample size that guarantees statistically robust results regarding the
number of channels.
1 INTRODUCTION
The analysis of electro-physiological signals gener-
ated by brain sources leads to a better understanding
of brain structures interaction and are useful in many
clinical applications or for brain-computer interfaces
(BCI) (Schomer and Lopes da Silva, 2011). One of
the most commonly used method to collect these sig-
nals is the scalp electroencephalogram (EEG). The
EEG consists in several signals recorded simultane-
ously using electrodes placed on the scalp (see fig.1).
The electrical activity of the brain sources is in fact
propagated through the anatomical structures and the
resulting EEG is a mixture (with unknown or diffi-
cult to model parameters) of brain sources and other
electro-physiological disturbances, often with a low
signal to noise ratio (SNR) (Sanei and Chambers,
2007).
The blind source separation (BSS) is a nowa-
days well established method to solve this problem,
as it can estimate both the mixing model and origi-
nal sources (Cichocki and Amari, 2002). In particu-
lar, approaches based on High Order Statistics (HOS)
such as Independent Component Analysis (ICA) are
common methods in this context and have been very
useful for denoising purpose or brain sources identi-
fication. However, the performances of these algo-
rithms are highly dependent on their pre-conditioning
given by 1) the data length chosen regarding the num-
ber of channels, and 2) the necessary decorrelation
step on which they are based. In this paper we eval-
uate the sensitivity to this pre-conditioning for three
popular ICA algorithms based on HOS: FastICA, Ex-
tended InfoMax and JADER.
1) The use of BSS on EEG signals implicitly as-
sumes that the estimated statistics are meaningful.
In order to ensure the reliability of these statistics,
different authors propose optimal sample sizes (i.e.
EEG signal time points), generally equal to k × n
2
where n is number of channels and k is some em-
pirical constant varying from 5 to 32 (Särelä and Vi-
gario, 2003; Onton and Makeig, 2006; Delorme and
Makeig, 2004). If these assumptions are correct, large
amount of channels requires huge sample sizes, pro-
cessing and time resources. On the other hand, EEG
signals are at most short term stationary, so it would
be interesting to find a sufficient inferior bound for
the number of necessary samples. The first question
is then how to define a minimum sample size that
provides reliable estimation of sources and mixing
55
Korats G., Le Cam S. and Ranta R..
IMPACT OF WINDOW LENGTH AND DECORRELATION STEP ON ICA ALGORITHMS FOR EEG BLIND SOURCE SEPARATION.
DOI: 10.5220/0003780000550060
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2012), pages 55-60
ISBN: 978-989-8425-89-8
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

model.
2) A second question addressed in this paper con-
cerns the stability (robustness) of the BSS results. As
it will be explained in the next sections, BSS includes
an optimization step. The results of this optimiza-
tion to some algorithms might depend on the initial-
ization of the algorithm. In the EEG and BSS litera-
ture (Palmer, 2010), some authors observed that using
different initializations (different decorrelation meth-
ods like classical whitening or sphering), the results
are more or less biologically plausible (thus implic-
itly different). The second auxiliary objective of this
paper is then to evaluate the statistical robustness of
several well known BSS algorithms to the initializa-
tion (decorrelation) step.
2 PROBLEM STATEMENT
2.1 EEG Mixing Model
Classical EEG generation and acquisition model is
presented in Figure 1. It is widely accepted that the
signals collected by the sensors are linear mixtures of
the sources (Sanei and Chambers, 2007).
Figure 1: EEG linear model.
Subsequently, the EEG mixture can be written as
X = AS, (1)
where X are the observations (electrodes), A is the
mixing system (anatomical structure) and S are the
original sources.
2.2 EEG Separation Model
We restrain in this paper to classical well determined
mixtures, where the number of channels is equal to
the number of underlying sources. In this case, BSS
gives the linear transformation (separating) matrix H
and the output signal vector Y = HX, containing
source estimates. Ideally, the global system matrix
G = HA between the original sources S and their es-
timates Y will be a permuted scaled identity matrix,
as it can be proven that the order and the original am-
plitude of the sources cannot be recovered (Cichocki
and Amari, 2002).
In all BSS methods, the matrix H is obtained as
a product of two statistically based linear transforms:
H = JW with
• W performing data orthogonalization: whiten-
ing/sphering,
• J performing data rotation : independence maxi-
mization via higher-order statistics (HOS) or joint
decorrelation of several time (frequency) intervals
The first step (data decorrelation) can be seen as an
initialization for the second step. In theory any or-
thogonalization technique can be used to initialize the
second step but in this paper we will focus on two
popular decorrelation techniques: whitening (classi-
cal solution) and sphering (assumed to be more bio-
logically plausible (Palmer, 2010)).
2.2.1 BSS Initialization: Whitening/Sphering
Whitening. In general EEG signals X are correlated
so their covariance Σ will not be a diagonal matrix and
their variances will not be normalized. Data whiten-
ing means projection in the eigenspace and normali-
sation of variances. The whitening transform can be
computed from the covariance matrix of the data X
(assumed zero-mean): Σ = E{XX
T
}.
Write the eigen-decomposition of Σ as
Σ = ΦΛΦ
T
, (2)
with Λ the diagonal matrix of eigenvalues and Φ the
eigenvectors matrix. Eigenvectors form a new or-
thogonal coordinate system in which the data are pre-
sented. The matrix Φ thus diagonalizes the covari-
ance matrix of X. Final whitening is obtained by sim-
ply multiplying by scale factor Λ
−
1
2
:
X
w
= Λ
−
1
2
Φ
T
X. (3)
After (3), the signals are orthogonal and with unit
variances (4) (Figure 2(c)).
E{
˜
X
w
˜
X
w
T
} = I. (4)
Sphering. Data sphering completes whitening by
rotating data back to the coordinate system defined
by principal components of the correlated data (Fig-
ure 2(d)). We can say that sphered data are turned as
close as possible to the observed data. To estimate the
sphering matrix we only need to multiply the whiten-
ing matrix with the eigenvector matrix Φ (Vaseghi and
Jetelová, 2006)
X
sph
= ΦΛ
−
1
2
Φ
T
X. (5)
BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing
56

(a) Original sources (b) Mixed data
(c) Whitened data (d) Sphered data
Figure 2: Example of different decorrelation approaches for
two signals
2.3 Optimization (Rotation)
Second step would be finding a rotation matrix J
to be applied to the decorrelated data (whitened or
sphered) in order to maximize their independence.
Rotation can be done using second order statistics
(SOS) using joint decorrelations and/or using HOS
cost functions. We restrain here to the second (HOS)
approach
1
. Several cost functions and optimization
techniques were described in the literature (see for
example (Cichocki and Amari, 2002; Delorme and
Makeig, 2004)). Among the most well known and
used in EEG applications, we can cite FastICA (neg-
entropy maximization (Hyvärinen, 1999)), Extended
InfoMax (mutual information minimization (Bell and
Sejnowsky, 1995)) and JADE/JADER (joint diagonal-
ization of fourth order cumulant matrices (Smekhov
and Yeredor, 2004)).
Specifically, in this paper we test the performances
and the robustness of the three cited ICA algorithms
with respect to the sample size and the initialization
step.
1
As described in the next section, in our simulations
we used random non-Gaussian stationary data, without any
time-frequency structure. Therefore algorithms based on
SOS as SOBI, SOBI-RO and AMUSE were not used.
3 PERFORMANCE EVALUATION
CRITERIA
3.1 Reliable Estimate of the
Covariance: Riemannian
Likelihood
As noted before, BSS model consists of decorrelation
and rotation. Both steps are based on statistical es-
timates. The first step is common for all algorithms
and relies on the estimation of the covariance matrix.
Therefore it is necessary to have reliable estimates of
this matrix. In other words, given a known covariance
matrix Σ, we want to evaluate the minimum sample
size m necessary to obtain a covariance matrix estima-
tion
ˆ
Σ
m
close enough to the original one with respect
to a distance that we have to define.
We propose here an original distance measure be-
tween the true and the estimated covariance matrices,
inspired from digital image processing and computer
vision techniques (Wu et al., 2008). In the context
of object tracking and texture description, a distance
measure is used to estimate whether an observed ob-
ject or region corresponds to a given covariance de-
scriptor. To estimate similarity between matrices re-
spectively corresponding to the target model and the
candidate, and knowing that covariance matrices are
symmetric positive definite, the following general
2
distance measure can be used:
d
2
(
ˆ
Σ
m
, Σ) = tr
log
2
ˆ
Σ
m
−
1
2
Σ
ˆ
Σ
m
−
1
2
(6)
An exponential function of the distance is adopted as
the local likelihood
p(Σ
m
) ∝ exp{−λ · d
2
(Σ,
ˆ
Σ
m
)}. (7)
In all the test procedures reported in this paper, we
fixed the parameter λ to the constant value λ = 0.5 as
proposed in literature (Wu et al., 2008). This p(Σ
m
)
value varies between 0 and 1, 1 meaning perfect esti-
mation (Σ =
ˆ
Σ
m
). A p(Σ
m
) value of 0.95 is considered
as a well chosen threshold above which the covariance
matrices are considered to be equal.
3.2 Separability Performance Index
In order to measure the global performance of BSS al-
gorithms (orthogonalization plus rotation), we use the
performance index (PI) (Cichocki and Amari, 2002)
defined by
2
on Riemannian manifolds
IMPACT OF WINDOW LENGTH AND DECORRELATION STEP ON ICA ALGORITHMS FOR EEG BLIND
SOURCE SEPARATION
57
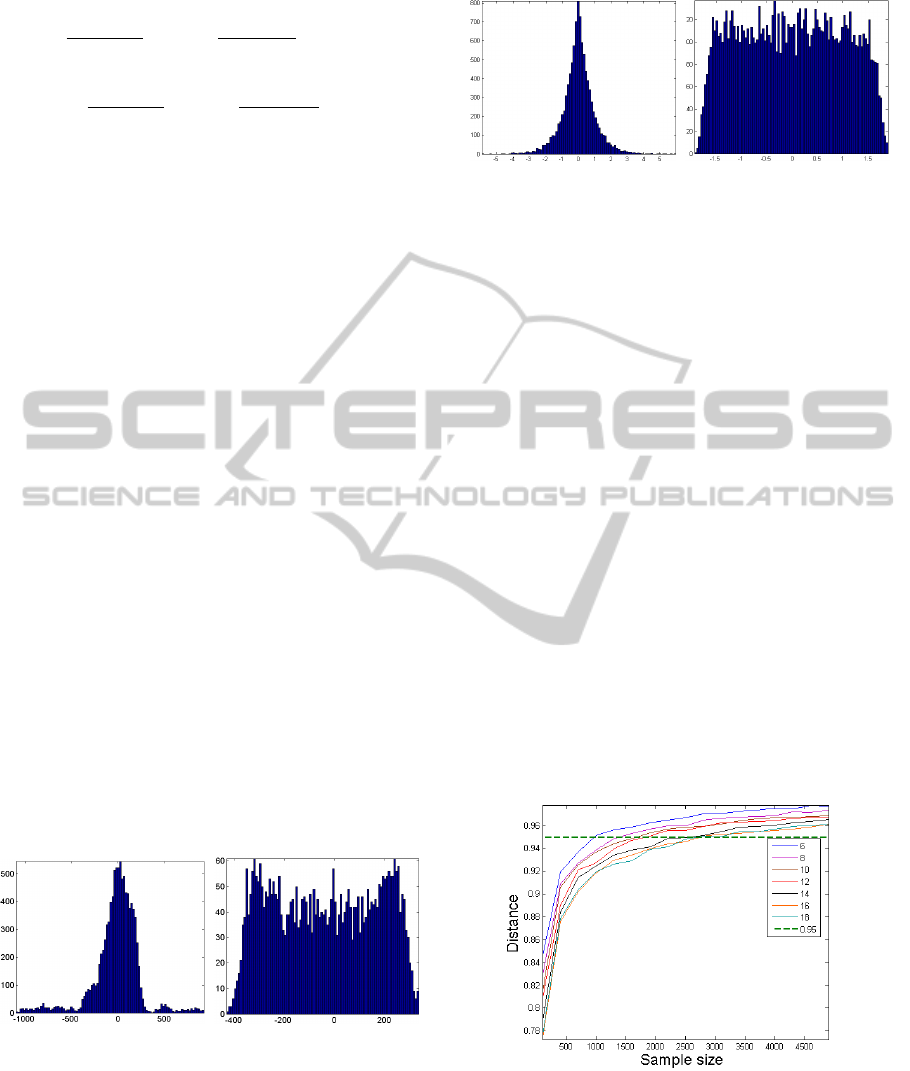
PI =
1
2n(n − 1)
n
∑
i=1
n
∑
j=1
|g
i j
|
max
k
|g
ik
|
− 1
!
+
1
2n(n − 1)
n
∑
j=1
n
∑
i=1
|g
i j
|
max
k
|g
k j
|
− 1
!
(8)
where g
i j
is the (i, j)-element of the global system
matrix G = HA, max
k
|g
ik
| is the maximum value
among the absolute values of the elements in the ith
row of G and max
k
|g
k j
| is the maximum value among
the absolute values of the elements in the jth column
of G. When perfect separation is achieved, the per-
formance index is zero. In practice a PI under 10
−1
means that the separation result is reliable.
4 RESULTS AND DISCUSSION
4.1 Simulated Data
Simulated EEG was obtained by mixing simulated
sources. We have chosen to simulate stationary white
source signals, as the retrieval of time structures is not
the purpose of this work (in fact, in all the tested al-
gorithms, as in most of the HOS type methods, the
time structure is ignored). In order to have realistic
distributions of the sources, we analysed depth intra-
cerebral measures (SEEG). According to our observa-
tions (see also (Onton and Makeig, 2006; Särelä and
Vigario, 2003)), the distribution of the electrical brain
activity signals can be suitably modelled by General-
ized zero-mean Gaussians, as shown in fig. 3(a) and
fig. 3(b)). For this reason we randomly generated both
supergaussian (Laplace - Figure 4(a)) and subgaus-
sian (close to uniform (Figure 4(b))) distributions.
(a) Normal background (b) Oscillatory signal
Figure 3: Histograms of two SEEG samples.
Several simulations were made, using 6, 12 and
18 source signals. Half of the sources were gener-
ated as supergaussian and half as subgaussian. The
sources were afterwards mixed using a randomly gen-
erated mixing matrix A whose values vary in the
range [−1, ..., 1]. We then consider here the perfor-
(a) Supergaussian data (b) Subgaussian data
Figure 4: Histograms of generated data.
mance of each of the three ICA algorithms facing sim-
ulated stationary non-artefacted data.
One could argue that more realistic contexts
should have been simulated by using head models,
realistic neural sources and extra-cerebral artefacts in
order to generate the simulated channels. As the pur-
pose here is the determination of a minimum amount
of data needed for a reliable source separation in
favourable conditions (after an artefact elimination
step for example), we decided to use stationary ran-
domly mixed data for gaining more generality.
4.2 Reliable Estimate of the Covariance
This section presents the results of the covariance es-
timation robustness vs the length of the data. The dis-
tance between covariance matrices was computed us-
ing 6 from different sample sizes starting from 100
points till 5000 points. The likelihood was further
evaluated using 7. A constant threshold was empir-
ically fixed to p = 0.95 (Figure 5): likelihood values
above this threshold are assumed to guarantee good
estimation of covariances as stated in section 3.1.
Figure 5: Riemannian likelihood for different sample sizes.
Each curve corresponds to a different number of channels
(from 6 to 18). The threshold p = 0.95 is displayed as a
dotted line.
As it can be seen in Figure 6, this estimate is be-
tween the bounds given in the literature, close to the
upper bound (30n
2
) for low number of channels n but
BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing
58
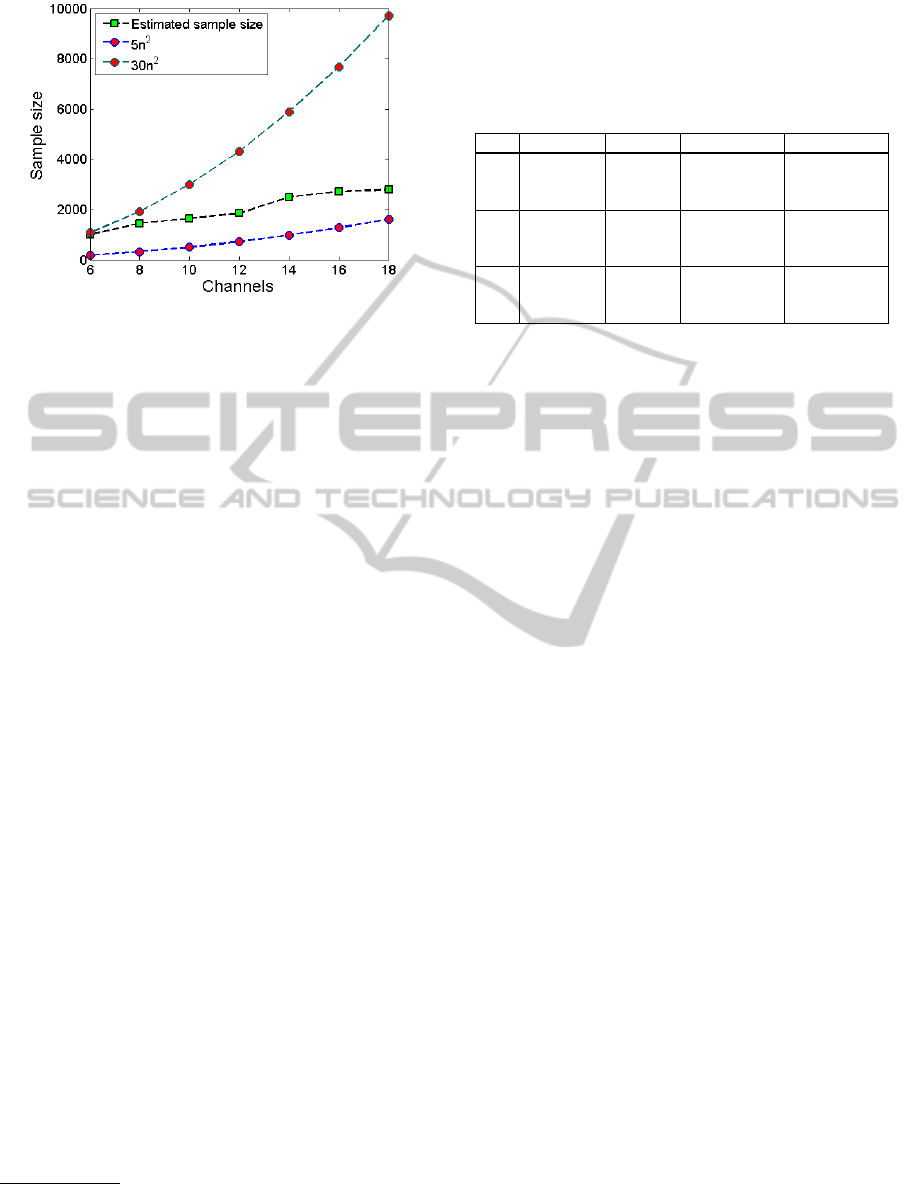
Figure 6: Sample size vs. number of channels for the pro-
posed decision rule (likelihood = 0.95).
increasing much slower. A possible way to interpret
the figure 6 is to use it as a decision rule: for a given
number of channels, one can estimate the minimum
number of data points necessary to have a reliable es-
timate of the covariance matrix and thus a reliable
whitening. This decision rule leads to data lengths
of about 1800 for 12 channels (2800 for 18 channels)
data points, that is about 7s (11s respectively) for a
sampling rate of 256 Hz. This range of time length
is more compatible with the stationarity hypothesis
than the values obtained using the 30n
2
rule (Delorme
and Makeig, 2004; Onton and Makeig, 2006). Indeed,
with this rule, we get 4320 (17s) and 9720 (38s) data
points respectively for 12 and 18 channels, which is
rather contradictory (at least in a realistic EEG setup)
with the assumption of stationarity on which BSS al-
gorithms are based
3
. As the next step (namely opti-
mization step) of the three considered algorithms is
based on HOS, these results are not sufficient to as-
sess good separation results. Next section discusses
the validity of the final unmixing results regarding the
data length given by the decision rule described in this
section.
4.3 Separability Performance
The global performances of ICA algorithms are here
evaluated using the PI given by (8). For the number
of points determined using the previous empirical rule
based on the covariance estimate (Riemannian likeli-
hood) and for different number of channels, the PI is
computed for each algorithm, the results being pre-
sented in table 1. We present two sets of results, ob-
tained considering either classical whitening or spher-
ing as the first decorrelation/initialization step. Recall
3
This observation is important especially for high reso-
lution EEG measures, when the number of channels can be
very high.
that our second objective was to assess the sensitivity
of the ICA algorithms to this initialization.
Table 1: PI values (mean and standard deviation) for differ-
ent number of channels and different ICA algorithms using
whitening (PI
w
) or sphering (PI
s
)
Ch Methods Length PI
w
± STD PI
s
± STD
6
FastICA
1000
0.102±0.02 0.104±0.02
EI-MAX 0.381±0.17 0.417±0.13
JADER 0.095±0.02 0.093±0.02
12
FastICA
1800
0.082±0.01 0.082±0.01
EI-MAX 0.359±0.13 0.349±0.13
JADER 0.072±0.01 0.074±0.01
18
FastICA
2800
0.067±0.01 0.067±0.01
EI-MAX 0.284±0.10 0.327±0.07
JADER 0.059±0.01 0.059±0.01
From Table 1 we conclude that separation perfor-
mance are satisfactory for FastICA and JADER as the
PI are close or below the threshold value of 0.1 for
every amount of channels considered. This reinforce
the validity of the empirical rule given by the results
section 4.2. In addition, according to table 1, PI val-
ues indicate better performances when the number of
channels is increasing with respect to our empirical
rule. This could suggest that our proposed criterion
could be relaxed and the number of points could be re-
duced further. But, on the other hand, one must take
into account that these tests are performed on simu-
lated stationary random data: if outliers are present,
HOS estimates are more affected than the SOS es-
timations that used to define our threshold, thus a
higher amount of points might be needed for HOS re-
liable estimation.
We have to notice here that in all simulations Ex-
tended InfoMax seems to provide worse results than
the two other tested algorithms, confirming the results
presented in (Ma et al., 2006). This phenomenon ap-
pears because of our choice of the simulated data. In-
deed, because of the use of subgaussian sources, the
algorithm (even in the extended version) needs more
data points in order to give reliable results. The evo-
lution of the PI for this algorithm, as a function of
the length of the data, is displayed in Figure 7. Em-
pirically, one can say that the 30n
2
rule seems to be
adapted for the Extended InfoMax algorithm, but ap-
parently too strong for the two others.
Table 1 allows to conclude also that each algo-
rithm is showing similar separability performance re-
gardless of the decorrelation step (whitening or spher-
ing). As it was expected, the optimization step is
then not sensitive to the initialization point set by the
decorrelation step for this kind of simulated stationary
non artefacted data. It would be interesting to test fur-
ther the robustness of these ICA algorithms when fac-
ing more realistic EEG like data. Such a study would
come to confirm or infirm the assumption made in a
IMPACT OF WINDOW LENGTH AND DECORRELATION STEP ON ICA ALGORITHMS FOR EEG BLIND
SOURCE SEPARATION
59
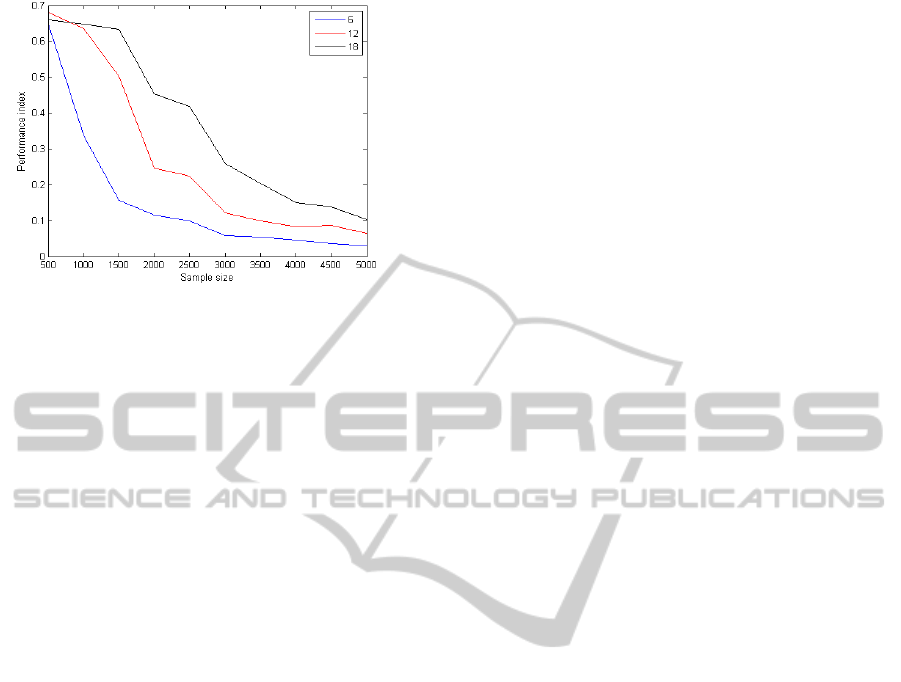
Figure 7: Extended InfoMax PI evolution for different num-
ber of channels as a function of the data length.
previous work (Palmer, 2010) stating that, for EEG
signals, using sphering instead of classical whitening
would result in more physiologically plausible sepa-
rated sources (i.e. more dipolar).
5 CONCLUSIONS AND FUTURE
WORK
Three popular ICA algorithms, often used to anal-
yse EEG signals, have been tested for different data
lengths and number of signals. The main objective
was to define a low bound of data length for robust
separation results, in order to take into account the
short term stationarity of the EEG signals. The re-
sults on simulated mixtures of subgaussian and su-
pergaussian sources are significant enough to extract
an empirical rule for the minimum data length, de-
pending on the number of channels. This result is
based on an original distance measure inspired by the
computer vision community and leads to a reasonable
time length (approximately 10s for 18 channels, sam-
pled at 256 Hz). An auxiliary objective was to test the
convergence robustness of these algorithms for differ-
ent initializations (whitening or sphering). Separation
Performance Index turns out to be similar whether
the decorrelation step is performed using sphering or
whitening method, confirming the robustness of these
algorithms.
Still, these results are not sufficient to conclude
on the impact of different decorrelation methods on
real EEG signals. We are considering further work on
EEG-like (dipolar mixtures) simulated data corrupted
with noise, in order to evaluate the importance of the
decorrelation step from a physiological point of view
(source dipolarity). If such sensitivity is confirmed,
a longer term ambition would be to find an adequate
decorrelation scheme that guarantees the convergence
of ICA algorithms to plausible physiological sources.
Finally, an immediate perspective would be to
extend our study to more HOS algorithms and
more channels, but also to use more realistic time-
structured data allowing the evaluation of SOS BSS
algorithms (SOBI and similar).
REFERENCES
Bell, A. and Sejnowsky, T. (1995). An information-
maximization approach to blind separation and blind
deconvolution. Neural Computation, 7(6):1129–1159.
Cichocki, A. and Amari, S.-I. (2002). Adaptive Blind Signal
and Image Processing. Wiley-Interscience.
Delorme, A. and Makeig, S. (2004). EEGLab: an
open source toolbox for analysis of single-trial EEG
dynamics including independent component analy-
sis. Journal of Neuroscience Methods, 134(1):9–21.
http://sccn.ucsd.edu/wiki/EEGLAB.
Hyvärinen, A. (1999). Fast and robust fixed-point algo-
rithms for independent component analysis. IEEE
Transactions on Neural Networks, 10(3):626–634.
Ma, J., Gao, D., Ge, F., and Amari, S.-i. (2006). A one-bit-
matching learning algorithm for independent compo-
nent analysis. In Rosca, J., Erdogmus, D., Príncipe,
J., and Haykin, S., editors, Independent Component
Analysis and Blind Signal Separation, volume 3889 of
Lecture Notes in Computer Science, pages 173–180.
Springer Berlin / Heidelberg.
Onton, J. and Makeig, S. (2006). Information-based mod-
eling of event-related brain dynamics. In Neuper, C.
and Klimesch, W., editors, Event-Related Dynamics of
Brain Oscillations, volume 159 of Progress in Brain
Research, pages 99 – 120. Elsevier.
Palmer, J. e. a. (2010). Independent component analysis
of high-density scalp EEG recordings. In Indepen-
dent Component Analysis of High-density Scalp EEG
Recordings, 10th EEGLAB Workshop, Jyvaskyla, Fin-
land.
Sanei, S. and Chambers, J. (2007). EEG signal processing.
Wiley-Interscience.
Schomer, D. and Lopes da Silva, F. (2011). Niedermey-
ers’s Electroenephalography: Basic Principles, Clini-
cal Applications and Related Fields. Wolters Kluwer,
Lippincott Willimas & Wilkins, 6th edition.
Smekhov, A. and Yeredor, A. (2004). Optimization of
JADE using a novel optimally weighted joint diago-
nalization approach. In Proc. EUSIPCO, pages 221–
224.
Särelä, J. and Vigario, R. (2003). Overlearning in marginal
distribution-based ICA: Analysis and solutions. Jour-
nal of Machine Learning Research, 4:1447–1469.
Vaseghi, S. and Jetelová, H. (2006). Principal and inde-
pendent component analysis in image processing. In
Proceedings of the 14th ACM International Confer-
ence on Mobile Computing and Networking (MOBI-
COM’06), pages 1–5. Citeseer.
Wu, Y., Wu, B., Liu, J., and Lu, H. (2008). Probabilistic
tracking on Riemannian manifolds. In Pattern Recog-
nition, 2008. ICPR 2008. 19th International Confer-
ence on, pages 1–4. IEEE.
BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing
60
