
COMPUTATION OF THE NORMALIZED COMPRESSION
DISTANCE OF DNA SEQUENCES USING A MIXTURE OF
FINITE-CONTEXT MODELS
Diogo Pratas, Armando J. Pinho and Sara P. Garcia
Signal Processing Lab, IEETA/DETI, University of Aveiro, 3810–193 Aveiro, Portugal
Keywords:
Normalized-compression distance, Finite-context models, Human chromosomal similarity.
Abstract:
A compression-based similarity measure assesses the similarity between two objects using the number of bits
needed to describe one of them when a description of the other is available. For being effective, these measures
have to rely on “normal” compression algorithms, roughly meaning that they have to be able to build an internal
model of the data being compressed. Often, we find that good “normal” compression methods are slow and
those that are fast do not provide acceptable results. In this paper, we propose a method for measuring the
similarity of DNA sequences that balances these two goals. The method relies on a mixture of finite-context
models and is compared with other methods, including XM, the state-of-the-art DNA compression technique.
Moreover, we present a comprehensive study of the inter-chromosomal similarity of the human genome.
1 INTRODUCTION
The work of Solomonoff, Kolmogorov, Chaitin
and others (Solomonoff, 1964; Kolmogorov, 1965;
Chaitin, 1966) on how to measure complexity has
been of paramount importance for several areas of
knowledge. However, because it is not computable,
the Kolmogorov complexity of A, K(A), is usually
approximated by some computable measure, such
as Lempel-Ziv based complexity measures (Lempel
and Ziv, 1976), linguistic complexity measures (Gor-
don, 2003) or compression-based complexity mea-
sures (Dix et al., 2007).
The Kolmogorov theory also leads to an approach
to the problem of measuring similarity. Li et al. pro-
posed a similarity metric (Li et al., 2004) based on an
information distance (Bennett et al., 1998), defined
as the length of the shortest binary program that is
needed to transform A and B into each other. This
distance depends not only on the Kolmogorov com-
plexity of A and B, K(A) and K(B), but also on con-
ditional complexities, for example K(A|B), that indi-
cates how complex A is when B is known. Because
this distance is based on the Kolmogorov complex-
ity (not computable), they proposed a practical ana-
log based on standard compressors, which they call
the normalized compression distance (Li et al., 2004),
represented by
NCD(A,B) =
C(AB) − min{C(A),C(B)}
max{C(A),C(B)}
, (1)
where C(A) and C(B) denote, respectively, the num-
ber of bits needed by the (lossless) compression pro-
gram to represent A and B, and C(AB) denotes the
number of bits required to compress the concatena-
tion of A and B.
According to (Li et al., 2004), a compression
method needs to be normal in order to be used in a
normalized compression distance. One of the condi-
tions for a compression method to be normal is that
the compression of AA (the concatenationof A with A)
should generate essentially the same number of bits
as the compression of A alone (Cilibrasi and Vit´anyi,
2005).
We propose a method for calculating the nor-
malized compression distance based on a mixture
of finite-context models. This DNA compression
method is in fact composed by a set of models, each of
different order, from which probabilities are averaged
using weights calculated through a recursive proce-
dure (described in Section 2).
This paper is organized as follows. In Section 2,
we describe our algorithm. In Section 3, we pro-
vide experimental results, including a comparation
of methods and a human genome inter-chromosomal
study. Finally, in Section 4, we draw some conclu-
sions.
308
Pratas D., J. Pinho A. and P. Garcia S..
COMPUTATION OF THE NORMALIZED COMPRESSION DISTANCE OF DNA SEQUENCES USING A MIXTURE OF FINITE-CONTEXT MODELS.
DOI: 10.5220/0003780203080311
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2012), pages 308-311
ISBN: 978-989-8425-90-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 MATERIALS AND METHODS
2.1 DNA Sequences
In this study, we used sequences from eleven
genomes obtained from the National Cen-
ter for Biotechnology Information (NCBI),
ftp://ftp.ncbi.nlm.nih.gov/genomes/. The genomes
are the following: Streptococcus pneumoniae,
R6 uid57859; Lactococcus lactis, Il1403 uid57671;
Shigella flexneri, 2a 301 uid62907; Salmonella
enterica, STyphi uid57793; Escherichia coli,
K 12 uid58979; Arabidopsis thaliana, AT; Saccha-
romyces cerevisiae, uid128; Schizosaccharomyces
pombe, uid127; Mus musculus, MGSCv37; Pan
troglodytes, B2.1.4; Homo sapiens, April 14 2003.
2.2 Finite-context Models
A finite-context model (FCM) of an information
source assigns probability estimates to the symbols
of the alphabet, according to a conditioning con-
text computed over a finite and fixed number, k > 0,
of past outcomes x
n−k+1..n
= x
n−k+1
... x
n
(order-k
FCM). In practice, the probability that the next out-
come x
n+1
is s ∈ A = {A,C,G,T}, is obtained using
the estimator
P(s|x
n−k+1..n
) =
C(s|x
n−k+1..n
) + α
C(x
n−k+1..n
) + 4α
, (2)
where C(s|x
n−k+1..n
) represents the number of times
that, in the past, symbol s was found having x
n−k+1..n
as the conditioning context, and where
C(x
n−k+1..n
) =
∑
a∈A
C(a|x
n−k+1..n
) (3)
is the total number of events that has occurred so far
in association with context x
n−k+1..n
. The per symbol
information content average provided by the FCM of
order-k, after having processed n symbols, is given by
H
k,n
= −
1
n
n−1
∑
i=0
log
2
P(x
i+1
|x
i−k+1..i
) bpb, (4)
where “bpb” stands for bits per base. When using sev-
eral models simultaneously, the H
k,n
can be viewed
as measures of the performance of those models until
that position. Therefore, the probability estimate can
be given by a weighted average of the probabilities
provided by each model, according to
P(x
n+1
) =
∑
k
P(x
n+1
|x
n−k+1..n
) w
k,n
, (5)
where w
k,n
denotes the weight assigned to model k
and
∑
k
w
k,n
= 1. For stationary sources, we could
compute weights such that w
k,n
= P(k|x
1..n
), i.e., ac-
cording to the probability that model k has generated
the sequence until that point. In that case, we would
get
w
k,n
= P(k|x
1..n
) ∝ P(x
1..n
|k)P(k), (6)
where P(x
1..n
|k) denotes the likelihood of sequence
x
1..n
being generated by model k and P(k) denotes the
prior probability of model k.
Since the DNA sequences are not stationary, a
good performance of a model in a certain region of
the sequence might not be attained in other regions
(Pratas and Pinho, 2011; Pinho et al., 2011a; Pinho
et al., 2011b). Hence, we used a mechanism for pro-
gressive forgetting of past measures, given by
p
k,n
= p
γ
k,n−1
P(x
n
|k,x
1..n−1
),w
k,n
= p
k,n
/
∑
k
p
k,n
.
3 EXPERIMENTAL RESULTS
In order to test our method we used a setup composed
of eight FCMs with orders k = 2,4,6, 8,10,12,14, 16.
The probabilities associated to the FCMs were esti-
mated using α = 1 for orders k = 2, 4, 6, 8, 10, 12
and with α = 0.05 for model orders k = 14, 16. The
performance forgetting parameter was set to γ = 0.99.
For comparasion, we used the competitive method
GZIP using the ”-best” option. This method is based
on LZ77 encoding (dictionary compression) and is
one of the most known methods in the compression
field. We used also, the current state-of-the-art in
DNA coding eXpert-Model, XM (Cao et al., 2007).
XM relies on a mixture of experts for providing sym-
bol by symbol probability estimates, which are then
used for driving an arithmetic encoder. The algo-
rithm comprises three types of experts: (1) order-2
Markov models; (2) order-1 context Markov mod-
els, i.e., Markov models that use statistical informa-
tion only of a recent past (typically, the 512 previ-
ous symbols); (3) the copy expert, that considers the
next symbol as part of a copied region from a partic-
ular offset. The probability estimates provided by the
set of experts are then combined using Bayesian av-
eraging and sent to the arithmetic encoder. We have
used this method with two different numbers of copy-
experts (50 and 200), to which we refer to as XM-50
and XM-200, respectively.
Using the methods mentioned above (FCM, GZIP,
XM-50 and XM-200), we have compressed the com-
bined sequences referred in the previous section. The
results are displayed in Table 1.
In this table we can verify that GZIP seems not
to be a good method to calculate the normalized
COMPUTATION OF THE NORMALIZED COMPRESSION DISTANCE OF DNA SEQUENCES USING A MIXTURE
OF FINITE-CONTEXT MODELS
309
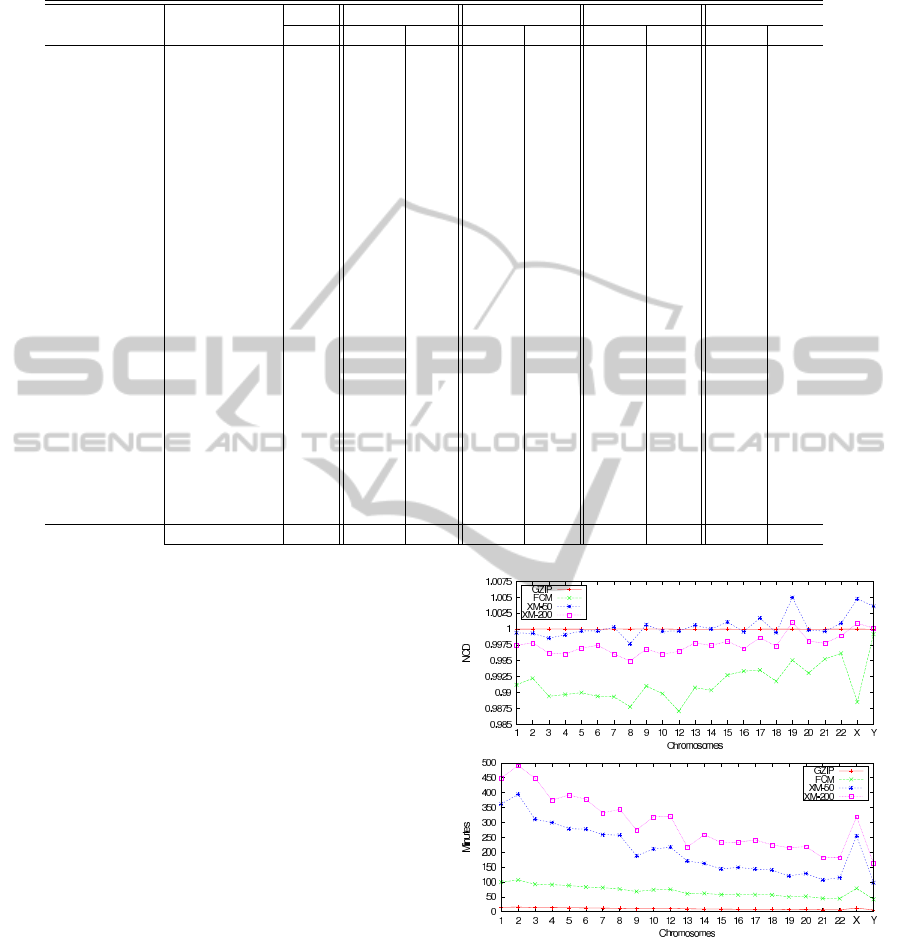
Table 1: The normalized compression distance (NCD) and the time (in minutes) required to compute it using different methods
on the concatenated sequences A and B. The bold values represent the best NCD values.
Sequence A Sequence B Size GZIP XM–50 XM–200 FCM
(Mb) NCD Time NCD Time NCD Time NCD Time
S. pneumoniae L. lactis 4.4 0.9987 0.2 0.9810 1.0 0.9797 1.0 1.0023 1.1
E. coli S. flexneri 9.3 0.9991 0.4 0.2298 2.7 0.2295 2.7 0.4176 2.2
E. coli S. enterica 9.5 0.9992 0.4 0.7776 2.8 0.7743 2.8 0.9748 2.3
A. thaliana C1 A. thaliana C2 50.0 0.9999 2.3 0.9809 19.6 0.9765 19.6 0.9877 10.9
A. thaliana C3 A. thaliana C4 42.0 0.9998 1.9 0.9763 14.0 0.9720 14.0 0.9837 10.7
S. cerevisiae C1 S. cerevisiae C2 1.0 0.9953 0.1 0.9898 0.1 0.9897 0.1 0.9922 0.3
S. cerevisiae C3 S. cerevisiae C4 1.8 0.9975 0.1 0.9945 0.2 0.9944 0.2 0.9947 0.5
S. cerevisiae C5 S. cerevisiae C6 0.8 0.9932 0.1 0.9861 0.1 0.9860 0.1 0.9884 0.2
S. pombe C1 S. pombe C2 10.1 0.9993 0.5 0.9855 2.5 0.9854 2.5 0.9872 2.4
S. pombe C2 S. pombe C3 7.0 0.9993 0.3 0.9941 1.9 0.9940 3.2 0.9948 1.7
M. musculus C5 P. troglodytes C5 325.8 0.9999 14.6 1.0125 370.8 1.0104 524.3 1.0090 90.4
M. musculus C5 H. sapiens C5 326.0 0.9999 14.6 1.0117 363.8 1.0102 542.3 1.0084 91.2
P. troglodytes C5 H. sapiens C5 354.8 0.9999 16.2 0.2475 401.0 0.1762 568.5 0.4743 100.0
H. sapiens C3 H. sapiens C5 371.1 0.9999 17.4 0.9988 441.1 0.9963 601.5 0.9891 104.9
H. sapiens C12 H. sapiens C9 244.5 0.9999 10.9 0.9995 195.7 0.9962 344.5 0.9905 66.9
H. sapiens C12 H. sapiens CY 152.1 0.9999 6.8 1.0029 104.0 0.9997 216.1 0.9992 41.5
H. sapiens C9 H. sapiens CY 137.9 0.9999 6.2 1.0039 73.6 1.0005 177.1 0.9995 38.1
H. sapiens C11 H. sapiens C12 260.0 0.9999 11.2 0.9997 216.8 0.9965 320.7 0.9871 75.3
H. sapiens CY P. troglodytes C5 200.1 0.9999 9.0 1.0004 152.8 0.9996 228.7 0.9971 55.6
H. sapiens C9 M. musculus C5 263.7 0.9999 10.7 1.0099 231.1 1.0080 268.8 1.0073 73.2
A. thaliana C2 S. cerevisiae C2 20.5 0.9998 0.9 1.0001 5.9 1.0001 167.2 1.0001 5.1
A. thaliana C3 S. pombe C3 25.9 0.9999 1.2 1.0002 7.8 1.0002 16.6 1.0004 6.4
S. cerevisiae C1 S. pombe C1 5.8 0.9993 0.3 0.9999 1.5 0.9999 11.3 1.0001 1.4
A. thaliana C4 S. pneumoniae 20.6 0.9998 1.0 1.0007 7.3 1.0007 10.0 1.0013 5.1
Total ≈ 2755 0.9992 123 0.9235 2507 0.9189 3874 0.9493 758
compression distance (NCD) on DNA sequences, be-
cause, as can be seen, it does not show any discrim-
inant capabilities. On the other hand, XM and FCM
seem to be able to distinguish the sequences.
The XM method seems to behave better than FCM
for small sequences and also for sequences that are
very similar. For example, the NCD of E. coli and
S. enterica has a value very small and we know from
(Zhao et al., 2007) that this has a biological justifi-
cation, since these genomes have a strong structural
relation. However, XM is much more time consum-
ing than FCM to accomplish the task.
The FCM method seems to perform better in
sequences that are somewhat dissimilar and large.
A few examples are the chromosomes from the
genomes: H. sapiens, P. troglodytes and M. muscu-
lus. Moreover, as already mentioned, it is more time
efficient than XM. To verify this observation, we have
ran a complete NCD for every H. sapiens chromo-
some. However, due to space restrictions, in Fig. 1,
we only present the NCD results of chromosome 11
with the rest of the chromosomes (H. sapiens).
In Fig. 1, it is possible to verify that FCM pro-
vides the smallest NCD value and time, comparing
with XM, in all entries. Moreover, FCM reveals some
interesting results that are not unveiled by the other
approaches. This can be observed, e.g., in the relative
Figure 1: Normalized compression distance (NCD) for dif-
ferent methods between the human chromosome 11 and
each of all other human chromosomes (top graph, the NCD
value, bottom graph, the time required).
position of the NCD values regarding the similarity
between chromosome 11 and chromosome X, and be-
tween chromosome 11 and chromosome 12.
We have also studied the inter-chromosomal sim-
ilarities in the H. sapiens genome, has it can be seen
in Fig. 2. There are some aspects that we should point
BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms
310

Figure 2: The Human genome inter-chromosomal similar-
ity heat map. On the right side is a bar that indicates the
strength of similarity (highest intensity at the top). The axes
of x and y represent chromosomes.
out: the sexual chromosomes (X-Y) have the larger
similarity among all chromosomes; looking into auto-
somes, the larger similarity is in chromosomes 18/21;
chromosome 12, 18 and X have the overall chromoso-
mal relation; there are relevant similarities is the fol-
lowing pairs: 3/4, 5/6, 11/12, 17/20 and 18/21.
4 CONCLUSIONS
We have developed a method for computing the nor-
malized compression distance based on a mixture
of finite context models. We have shown that this
method is, on average, better than the state-of-the-
art XM on large and not very similar sequences (the
human genome, for example). Moreover, the time
required to accomplish the task is much lower than
in the XM approach. Using the proposed method,
we have also studied the similarity between chro-
mosomes of the human genome, revealing several
pointed similarities among these chromosomes.
In the future, we intend to create a hybrid solu-
tion using the copy expert and the mixture of finite-
context models, since these two methods proved to be
of strong functionality and complementarity.
ACKNOWLEDGEMENTS
This work was supported in part by the grant
with the COMPETE reference FCOMP-01-0124-
FEDER-010099 (FCT reference PTDC/EIA-EIA/
103099/2008). Sara P. Garcia acknowledges funding
from the European Social Fund and the Portuguese
Ministry of Education.
REFERENCES
Bennett, C. H., G´acs, P., Vit´anyi, M. L. P. M. B., and Zurek,
W. H. (1998). Information distance. IEEE Trans. on
Information Theory, 44(4):1407–1423.
Cao, M. D., Dix, T. I., Allison, L., and Mears, C. (2007).
A simple statistical algorithm for biological sequence
compression. In Proc. of DCC-2007, pages 43–52,
Snowbird, Utah.
Chaitin, G. J. (1966). On the length of programs for com-
puting finite binary sequences. Journal of the ACM,
13:547–569.
Cilibrasi, R. and Vit´anyi, P. M. B. (2005). Clustering by
compression. IEEE Trans. on Information Theory,
51(4):1523–1545.
Dix, T. I., Powell, D. R., Allison, L., Bernal, J., Jaeger,
S., and Stern, L. (2007). Comparative analysis of
long DNA sequences by per element information con-
tent using different contexts. BMC Bioinformatics,
8(Suppl. 2):S10.
Gordon, G. (2003). Multi-dimensional linguistic complex-
ity. Journal of Biomolecular Structure & Dynamics,
20(6):747–750.
Kolmogorov, A. N. (1965). Three approaches to the quanti-
tative definition of information. Problems of Informa-
tion Transmission, 1(1):1–7.
Lempel, A. and Ziv, J. (1976). On the complexity of fi-
nite sequences. IEEE Trans. on Information Theory,
22(1):75–81.
Li, M., Chen, X., Li, X., Ma, B., and Vit´anyi, P. M. B.
(2004). The similarity metric. IEEE Trans. on Infor-
mation Theory, 50(12):3250–3264.
Pinho, A. J., Pratas, D., and Ferreira, P. J. S. G. (2011a).
Bacteria DNA sequence compression using a mixture
of finite-context models. In Proc. of the IEEE Work-
shop on SSP, Nice.
Pinho, A. J., Pratas, D., Ferreira, P. J. S. G., and Garcia,
S. P. (2011b). Symbolic to numerical conversion of
DNA sequences using finite-context models. In Proc.
of EUSIPCO-2011, Barcelona.
Pratas, D. and Pinho, A. J. (2011). Compressing the human
genome using exclusively Markov models. In PACBB
2011, vol 93, pages 213–220.
Solomonoff, R. J. (1964). A formal theory of inductive in-
ference. Part I and II. Information and Control, 7(1
and 2):1–22 and 224–254.
Zhao, G., Perepelov, A. V., Senchenkova, et al. (2007).
Structural relation of the antigenic polysaccharides of
E. coli o40, S. dysenteriae type 9, and E. coli k47.
Carbohydrate Research, 342(9):1275–1279.
COMPUTATION OF THE NORMALIZED COMPRESSION DISTANCE OF DNA SEQUENCES USING A MIXTURE
OF FINITE-CONTEXT MODELS
311
