
HIERARCHICAL DYNAMIC MODEL FOR
HUMAN DAILY ACTIVITY RECOGNITION
Blanca Florentino-Lia
˜
no, Niamh O’Mahony and Antonio Art
´
es-Rodr
´
ıguez
Department of Signal and Communications Theory, Universidad Carlos III de Madrid, Madrid, Spain
Keywords:
Activity recognition, Inertial sensors, Ambulatory monitoring.
Abstract:
This work deals with the task of human daily activity recognition using miniature inertial sensors. The pro-
posed method is based on the development of a hierarchical dynamic model, incorporating both inter-activity
and intra-activity dynamics, thereby exploiting the inherently dynamic nature of the problem to aid the clas-
sification task. The method uses raw acceleration and angular velocity signals, directly recorded by inertial
sensors, bypassing commonly used feature extraction and selection techniques and, thus, keeping all informa-
tion regarding the dynamics of the signals. Classification results show a competitive performance compared
to state-of-the-art methods.
1 INTRODUCTION
The task of human activity recognition using wear-
able inertial sensors is becoming popular in ap-
plications which require context-aware monitoring,
such as ambulatory monitoring of elderly patients
and home-based rehabilitation. In such applica-
tions, knowledge of the activity being carried out by
the patient is vital for providing the context within
which the patient is being monitored and this context-
awareness can help to overcome the limitations asso-
ciated with the use of self reporting in medical assess-
ment. One of the major advantages of such systems is
that they can reduce the frequency of patients’ visits
to medical centers, improving their quality of life and
reducing medical costs.
There are two main methods for human activ-
ity recognition: vision-based, e.g. (Moeslund et al.,
2006), and inertial sensor-based, e.g. (Sabatini et al.,
2005). The main disadvantages of vision-based sys-
tems are that they can only be used in a confined
space, they interfere with the privacy of the individual
and they produce an excessive amount of information
that must be processed. On the other hand, due to re-
cent advances in sensor technologies, inertial sensor
devices have become compact and portable enough
to be unobtrusively attached to the human body. For
this reason, wearable miniature inertial sensors, in-
corporating accelerometers and gyroscopes, have be-
came the ideal platform for human movement moni-
toring (Sabatini et al., 2005), falls detection (Wu and
Xue, 2008), medical diagnosis and treatment (Pow-
ell et al., 2007), and tele-rehabilitation (Winters and
Wang, 2003).
Nowadays, the main challenge in activity recogni-
tion is the development of a system for real-life mon-
itoring applications using wearable sensors. Long
term recording capabilities and unobtrusiveness are
the primary requirements of such systems. The main
constraint for the long term recording capabilities re-
quirement is the battery life of the sensor devices.
This drawback is even more important in real-time
applications, such as fall detection systems. The pro-
cessing of the data in real time can either be done
by the sensor, if it has an on-board processor, or by
transmitting the data wirelessly from the sensor to an
external processor. Both cases result in high battery
consumption and the latter case also requires the pa-
tient to be confined within the range of the wireless
communication system. In order to make the sys-
tem as unobtrusive as possible, the number of sensors
placed on the body should be kept to a the minimum
despite the fact that the larger the number of sensors,
the more activities the system can recognize (Bao and
Intille, 2004). Thus, choosing the number of sensors
is a trade off between performance and usability.
Further to simply identifying which activities a
subject is carrying out, this work proposes to also pro-
vide information regarding of the dynamics of the ac-
tivity itself. There are two benefits to this approach:
(1) the intra-activity dynamics can aid the classifi-
cation task and (2) additional contextual information
61
Florentino-Liaño B., O’Mahony N. and Artés-Rodríguez A..
HIERARCHICAL DYNAMIC MODEL FOR HUMAN DAILY ACTIVITY RECOGNITION.
DOI: 10.5220/0003781900610068
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2012), pages 61-68
ISBN: 978-989-8425-89-8
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

could be gained from characteristics of the dynamic
behaviour. With this in mind, we propose a hierar-
chical dynamical model which takes into account two
levels of dynamics: inter-activity and intra-activity.
The model aims to represent the activities as intu-
itively as possible in terms of the patterns present in
the raw data from the sensors. Thus, not only are dif-
ferent activities recognized, but the “events” within a
given activity are also distinguished, for example, the
steps in the case of walking. Three different dynamic
models are described, each one pertaining to a partic-
ular type of activity: the first is for stationary activi-
ties like standing, sitting and lying; the second, for ac-
tive movements like walking and running, whilst the
third deals with short-time motions like jumping and
falling.
A further advantage of the proposed system is
that it uses raw signals directly from the sensor, thus
avoiding computationally expensive techniques such
as feature extraction and selection. Because the sys-
tem is designed to capture directly the dynamics of
the signals, activity recognition is achieved with high
accuracy whilst eliminating costly processing tech-
niques.
The paper is organized as follows: in Section 2
the activity recognition literature is reviewed. Section
3 describes the proposed hierarchical dynamic model.
The test procedure is outlined in Section 4, whilst in
Section 5 the results obtained with our model are pre-
sented. Section 6 provides a discussion of the oper-
ation of the proposed method. Finally, in Section 7,
conclusions and future lines of work are discussed.
2 BACKGROUND AND RELATED
WORK
2.1 Sensors and Feature Extraction
The previously published literature in the area of hu-
man activity recognition using inertial sensors is quite
extensive. Most of the published work follows a simi-
lar approach of data collection and processing, as out-
lined in this section.
Perhaps the first consideration in any activity
recognition system, is the selection of the type and the
number of sensors, as well as the positions on the hu-
man body where they will be worn. The simplest sen-
sor used in the recent literature is a triaxial accelerom-
eter (Han et al., 2010; Krishnan et al., 2008; He and
Jin, 2008; Khan et al., 2010). In (Frank et al., 2010;
Altun and Barshan, 2010; Zhu and Sheng, 2010), in-
ertial measurement units (IMU), combining triaxial
accelerometers and triaxial gyroscopes, are used to
provide measurements of specific force and angular
rate, respectively. As has been previously mentioned,
the larger the number of sensors used, the more activi-
ties the system can recognize. Similarly, the choice of
sensor positions on the body is crucial. In the case of
a single sensor, the most popular place is the waist, on
the belt or in the pocket of the trousers (Frank et al.,
2010; Han et al., 2010; He and Jin, 2008). In this
work, a single IMU placed on either the left or right
hip is considered for testing purposes, although the
model is not limited to this configuration.
The first processing step is, typically, focused on
the construction of a feature vector derived from the
raw signals of the sensor. In the literature, a large
number of different features have been reported as
being suitable for the classification task considered in
this work; (Preece et al., 2009) provides a comparison
of the most popular features. A common approach
is to extract many features (for example in (Krishnan
et al., 2008) thirty-nine features are extracted); then,
dimensionality reduction techniques such as Principal
Component Analysis (PCA) or Linear Discriminant
Analysis (LDA) are used to reduce the size of the fea-
ture vector before classification.
In addition to the processing required for feature
extraction and selection, another disadvantage of this
approach is that a predefined window length must be
determined to compute the features. Furthermore, an
overlap is often used between consecutive windows.
The selection of such parameters is somewhat arbi-
trary and there is a lack of agreement on the best
choice; in the literature, the window length varies
widely (e.g. from 16 msec (Han et al., 2010) to 6 sec
(Bao and Intille, 2004)), whilst a 50% overlap is com-
mon.
Once the feature vector has been computed from
the windowed signals, the next step is the develop-
ment of a model that is able to discriminate among
activities. The most popular methods that have been
used to solve this sequential supervised learning prob-
lem are batch supervised learning algorithms and Dy-
namic Bayesian Networks (DBN).
In (Altun and Barshan, 2010), a comparison of
classification results using various batch supervised
learning algorithms, including Bayesian Decision
Making (DBM), Least-Squares Method (LSM), k-
Nearest Neighbor (k-NN), Support Vector Machines
(SVM) and Artificial Neural Networks (ANN) can be
found. Batch supervised learning algorithms, which
ignore the dynamics of the signals, are not consid-
ered in this work. One reason for this is to bypass
the feature extraction step and, furthermore, it will be
seen that consideration the dynamics of the signals
BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing
62

can give useful information about the type of activity
that is being performed.
In the case of DBN, Hidden Markov Models
(HMM) are the most frequently used. The model pro-
posed in this work is based on HMMs and, so, the
next section will describe, briefly, the theory govern-
ing HMMs and discuss, in detail, their use in the task
of daily human activity recognition.
2.2 Hidden Markov Models
2.2.1 Background
A HMM (Rabiner, 1990) is a probabilistic model that
represents the joint distribution of the observations
and the unobserved (hidden) variable. In this work
the observations are continuous signals of accelera-
tion and angular velocity. The unobserved variable
must be discrete and its possible values are called
states. The proposed hierarchical model in this work,
defines two different unobserved variables: the activi-
ties (e.g. walking, running, etc.) and the events within
each activity. This will be explained in more detail in
the Section 3.
A first order HMM is characterized by the follow-
ing:
• N, the number of states in the model. The individ-
ual states are denoted as S = {S
1
, S
2
, . . . , S
N
}, and
the state at time t as q
t
.
• The state transition probability distribution ma-
trix, A = {a
i j
}. This is an N × N matrix where the
element, a
i j
, is the probability of making a transi-
tion from state S
i
to state S
j
:
a
i j
= P(q
t+1
= S
j
|q
t
= S
i
). (1)
• The emission distribution vector, B = {b
j
(O)},
where, for state j:
b
j
(O) =
M
∑
m=1
c
jm
N(O, µ
jm
, U
jm
), (2)
where O is the vector to be modeled, M is the
number of mixtures, c
jm
is the mixture coefficient
for the mth mixture in state j and N is any log-
concave or elliptically symetric density (in our
case we have selected a Gaussian density) with
mean vector µ
jm
and covariance matrix U
jm
for
the mth mixture component in state j.
• The initial state distribution π = {π
i
} where
π
i
= P(q
0
= S
i
) (3)
Thus, the HMM is defined by λ = (A, B, π).
For HMMs, the problem of learning the model
parameters is solved by the Baum-Welch algorithm
(Rabiner and Juang, 1993). The Viterbi algorithm
(Viterbi, 1967) is used to compute the most likely se-
quence of states, Q = q
0
q
1
. . . q
T
, from time t = 0 to
t = T and its probability, given the model and an ob-
servation sequence, O = O
0
O
1
. . . O
T
.
2.2.2 HMMs and Activity Recognition
In the literature, there are two main approaches to
solving the activity recognition task using HMMs.
In the first approach (Zhu and Sheng, 2010), only
the temporal dependency among activities is modeled
and there is just one HMM, whose number of states
is equal to the number of activities. This model is
very simple and is usually combined with batch su-
pervised learning algorithms. Modeling the temporal
dependencies among the activities allows the system
to model human behavior by forbidding impossible
transitions like, for example, a direct transition from
running to lying down. An example of this approach
can be found in (Zhu and Sheng, 2010) where the
classification is done in two steps; first, two ANNs are
used for determining whether or not the feature vec-
tor corresponds to a dynamic activity and whether the
movement is vertical or horizontal; then, the fusion of
these two outputs becomes the input to a HMM where
the states are the activities.
In the second approach (Han et al., 2010), one
HMM per activity is modeled. The number of states
of each HMM is a design parameter. The inference
step consists of computing the likelihood of a test se-
quence with each of the HMMs. The activity corre-
sponding to the HMM with the highest likelihood is
the chosen activity. The main drawback of this ap-
proach is that it is necessary to define a sequence size
in order to learn the models and to infer the test se-
quence. Well-defined sub-units do not exist in the
recorded IMU signals, since human activities are con-
tinuous and any given activity can have a highly vari-
able duration. The sequence size is often selected tak-
ing into account the time interval during which only
one activity exists. In (Han et al., 2010), this is set to
2 seconds. Some disadvantages of this approach are
the requirement to define the sequence size, that the
temporal dependency among activities is not modeled
and that the HMM of each activity does not represent
the activity itself but a sequence of, for example, 2
seconds of the activity. Thus, dynamic information
is lost by truncating movement patterns and rhythmic
movements.
To overcome this problem, (Oliver et al., 2002)
develop a Layered Hidden Markov Model (LHMM),
in which each layer of the architecture is connected to
the next layer via its inferential results. This represen-
tation segments the problem into distinct layers that
HIERARCHICAL DYNAMIC MODEL FOR HUMAN DAILY ACTIVITY RECOGNITION
63

operate at different temporal granularities. But, again,
the parameters of the HMMs do not give any intuitive
information about how the person is performing the
activity and it is necessary to arbitrarily define these
temporal granularities.
As has been shown in this section, there is no con-
sensus on the most discriminative features for use in
an activity recognition system. For this reason, it is
usual to extract a large number of features and, then,
use a dimensionality reduction technique. The ma-
jor drawback of this approach is the computational
cost. Moreover, it has been mentioned that the win-
dow length used to compute the features is another
design parameter that varies widely among previous
studies. With this in mind, this work aims to bypass
the feature extraction step and work directly with the
raw data produced by the sensor.
3 PROPOSED METHOD
The method proposed in this work consists of a hi-
erarchical dynamical model based on HMMs whose
inputs are the raw signals given directly by the sen-
sor. This model takes into account the temporal
dependencies among activities and models each ac-
tivity in terms of acceleration and angular velocity
signals. The hierarchical scheme concept has been
mentioned before in the activity recognition literature
(Khan et al., 2010). In their work, the term hierarchi-
cal is used because the learning process is done in two
steps. First, the type of the activity (static, dynamic
or transition) is recognized, using an ANN, and, then,
the activity itself is determined.
3.1 Hierarchical Dynamical Model
The final result of our hierarchical dynamical model
is a single HMM (λ
F
= (A
F
, B
F
, π
F
)). This final
HMM is built up of “sub”-HMMs, one for each ac-
tivity, which are joined to yield the final HMM. The
learning process is performed in two stages. In the
first stage the intra-activity dynamics are taken into
account, modeling each activity separately with a
unique “sub”-HMM and learning its parameters, as
described in Section 3.1.1. The second stage concate-
nates these HMMs, modeling inter-activity dynamics,
as outlined in Section 3.1.2.
3.1.1 Intra-activity Dynamics
At this level, the hidden variable represents the sig-
nificant events occurring during the activity. These
events are the internal states of the sub-HMMs of each
activity. The individual events, or states, of activity, Z,
are denoted by E
Z
= {E
Z
1
, ··· , E
Z
K
Z
} where K
Z
is the
number of states of activity, Z, and the state at time t
is denoted by e
t
.
In this first stage of the learning process, the joint
probability distribution of the observations, O, and
the events, e, given the activity, Z, (p(e, O|Z)) are
modeled:
p(e, O|Z) =
t
∏
p(O
t
|e
t
, Z)p(e
t
|e
t−1
, Z). (4)
Each activity can have a different number of events
and a different topology, as detailed in the following.
We propose three different topologies, depending
on the type of the activity. All of them have in com-
mon that they have two transient states (the first and
the last), that describe the transition from one activity
to another. Each activity must begin in the first state,
and once this state is left it cannot be returned to from
within the activity. The only possible transition from
the last state is to itself. This is achieved by forcing
the values of the model parameters to be:
• The transition matrix A
Z
of the activity Z:
A
Z
=
a
Z
11
a
Z
12
0 ··· 0
0 a
Z
22
a
Z
23
··· a
Z
2K
Z
0 0 a
Z
33
··· a
Z
3K
Z
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 0 ··· 1
(5)
• The initial state distribution vector:
π
Z
=
1 0 ··· 0
(6)
For stationary activities like standing, sitting and
lying, a left-right model with three states is proposed
(Figure 1). The first and the last states are the transient
states and the state in the middle models the perma-
nent state of being seated, for example.
The second model is designed for active move-
ments like walking and running (Figure 2). In this
case there are two intermediate states which represent
the pattern of stepping. These two states are fully
inter-connected in order to model the periodicity of
walking or running.
The last topology models short-time motions like
jumping and falling. This model is made up only of
transient states since there is neither a permanent ac-
tion nor a rhythmic movement (Figure 3).
3.1.2 Inter-activity Dynamics
Once the models of each activity have been defined,
they can be concatenated by means of their transient
states (Figure 4) defining the transition probabilities
BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing
64

E
2
# E
3
#
E
1
#
Figure 1: HMM topology for stationary activities.
E
3
#
E
2
#
E
4
#
E
1
#
Figure 2: HMM topology for active movements.
E
2
#
E
1
#
Figure 3: HMM topology for short-time motions.
RUN$
STANDING$
WALK$
Figure 4: Concatenation of the HMMs.
among activities. These transition probabilities model
human behavior; for example, the transition probabil-
ity from walking to standing is higher than the tran-
sition probability from walking to running. Never-
theless, if the activity recognition system is used to
monitor the elderly, the transition probability between
walking and running would be lower than that in the
case of monitoring children.
The result of the concatenation is a single HMM,
λ
F
= (A
F
, B
F
, π
F
), with twenty-one states, corre-
sponding to all events of all activities as follows:
running (states 1-4), walking (5-8), standing (9-11),
sitting (12-14), lying (15-17), jumping (18-19) and
falling (20-21). The state transition probability ma-
trix of the final model, A
F
, is built up following the
steps below:
(i) Set the transition probability matrixes of the
sub-HMMs in the diagonal transition probabil-
ity matrix of the final HMM:
A
F
=
A
Run
0 0 0 0 0 0
0 A
W lk
0 0 0 0 0
0 0 A
Std
0 0 0 0
0 0 0 A
Sit
0 0 0
0 0 0 0 A
Lie
0 0
0 0 0 0 0 A
Jmp
0
0 0 0 0 0 0 A
Fll
.
(7)
(ii) Connect the sub-HMMs. This step is straight-
forward, thanks to the definition of transient
states, since all the activities must begin at the
first state and end at the last state of their sub-
HMM. Thus, we set:
a
F
i j
= P(e
t+1
= S
j
|e
t
= S
i
)
= P(act
t+1
= Z
0
|act
t
= Z), (8)
for all i 6= j which satisfy the condition that S
i
is the last state of any activity, Z, and S
j
is the
first state of any other activity, Z
0
. For exam-
ple, to connect the sub-HMM of running to the
sub-HMM of walking, the value of the param-
eter a
F
45
= P(e
t+1
= E
walk
1
|e
t
= E
run
4
) of the fi-
nal HMM will be set to P(act
t+1
= walk|act
t
=
run).
(iii) Reset the self-transition probabilities corre-
sponding to the last event of each activity,
i.e. set:
a
F
j j
= 1 −
21
∑
m=1,m6= j
a
F
jm
(9)
for each j which satisfies the condition, S
j
∈
{E
run
4
, E
wlk
4
, E
Std
3
, E
Sit
3
, E
Lie
3
, E
Jmp
2
, E
Fll
2
}.
The emission probabilities of the final HMM, B
F
, are
the corresponding emission probabilities of each sub-
HMM, defined in the first stage of the learning pro-
cess.
Finally, the initial state distribution of the final
HMM, π
F
, is defined. In general, the value π
F
j
is set
to zero if S
j
does not correspond to the first event of
any sub-HMM. In this work, standing is always con-
sidered as the first position.
4 TEST PROCEDURE
4.1 Database Description
In order to facilitate comparison of results with state-
of-the-art results, the database available in (Frank
et al., 2010) has been used for testing the proposed
method. This database consists of 4 hours and 30
HIERARCHICAL DYNAMIC MODEL FOR HUMAN DAILY ACTIVITY RECOGNITION
65
minutes of activity data from 16 subjects (6 females
and 10 males) aged between 23 and 50 years. Data
were recorded in semi-naturalistic conditions. The
IMU was placed on a belt, either on the right or left
hip, providing 3-axis acceleration and 3-axis angular
velocity signals at a sampling rate of 100 Hz.
The activities labelled in the database are running,
walking, standing, sitting, lying, jumping, falling, as-
cending (from sitting to standing and from lying to
standing), descending, accelerating (from walking to
running) and decelerating (from running to walking).
In the database, there are both training sequences and
benchmark sequences. There are two benchmark se-
quences from two different subjects (Emil and Sinja).
Emil has the IMU placed on his right side and Sinja,
on her left side. These benchmark sequences consist
of a succession of activities. More details of the data
collection and labeling can be found in (Frank et al.,
2010).
4.2 Training
For the purposes of learning the model for each ac-
tivity, sequences corresponding to one single activ-
ity were extracted from the database, to be used as
training data. Therefore, for each activity there are a
different number of sequences with different lengths.
Each HMM learned its parameters using the Baum-
Welsh algorithm. The emission distributions were de-
fined as mixtures of two gaussian distributions with
diagonal covariance matrix.
4.3 Evaluation
The hierarchical dynamic model was tested, using
the benchmark sequences, which were decimated by
a factor of 4. This means that the model can be
used with acceleration and angular velocity signals
recorded at a sampling rate of 25 Hz, allowing the
sensor device to consume less battery. In order to
compute the most likely sequence of events given the
observation sequence, the Viterbi algorithm was used.
Using the knowledge of which set of events corre-
spond to each activity, finally, the sequence of activi-
ties was obtained.
5 RESULTS
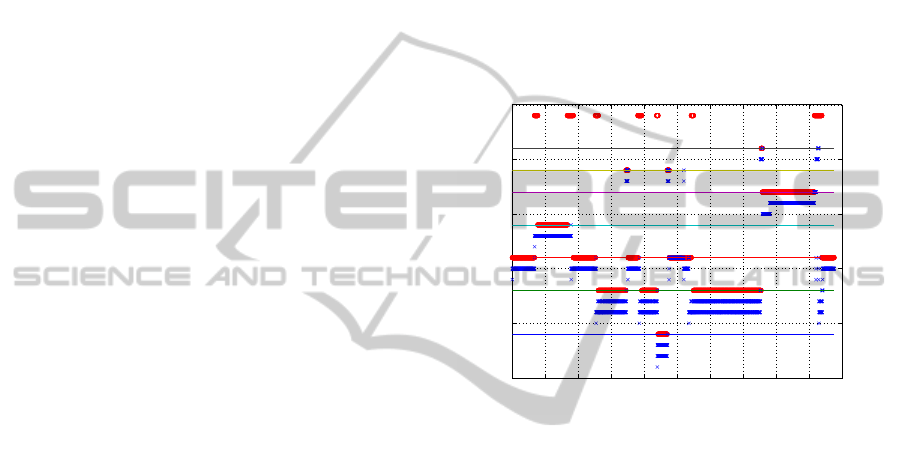
Figure 5 shows the sequence of events for the bench-
mark sequence of Emil. The blue crosses correspond
to the events inferred by the Viterbi algorithm. Events
1 to 4 belong to the activity running, 5 to 8 to the ac-
tivity walking and so on, as listed in Section 3.1.2.
The red circles are the true, labelled activities and
they are aligned in the graph with the last event of
each activity. It should be remembered, here, that
the model proposed in this work does not consider
as activities, the “transition” activities labelled in the
database (i.e. ascending, descending, accelerating and
decelerating), since these events are inherently dealt
with by means of the transient events in the hierar-
chical dynamic model. It can be seen from Figure 5
that the transition activities have, indeed, been incor-
porated by the proposed algorithm into the inferred
intra-activity events. The figure shows good agree-
ment between true and inferred activities.
0 20 40 60 80 100 120 140 160 180 200
0
5
10
15
20
25
Time (sec)
Events
Emil (f
s
=25Hz)
RUNNING
WALKING
STANDING
SITTING
LYING
JUMP
FALL
TRANSITIONS
Figure 5: Sequence of events inferred for Emil’s benchmark
sequence.
Tables 1 and 2 show the precision and recall values
of each activity for the benchmark sequences of Emil
and Sinja, respectively. The precision of activity, Z,
is measured as number of samples classified correctly
as activity, Z, divided by the total number of samples
with inferred label equal to Z. The recall parameter is
the number of samples correctly classified as activity,
Z, divided by the number of samples whose true label
is Z.
For comparison, Table 3 shows the performance
reported in (Frank et al., 2010), relative to which the
performance of the proposed algorithm is seen to be
competitive.
6 DISCUSSION
The results obtained for Sinja (table 2) are lower than
those for Emil (table 1) because our model does not
deal specifically with the location of the sensor. The
number of training sequences recorded with the sen-
sor placed on the right side was greater than those
recorded on the left side, so the model has learned,
BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing
66

Table 1: Recall and precision for Emil’s benchmark se-
quence (IMU placed on the right side).
Activity Recall Precision
(%) (%)
Running 100 95
Walking 99 97
Standing 96 99
Sitting 100 100
Lying 99 100
Jump 72 96
Fall 100 60
Table 2: Recall and precision for Sinja’s benchmark se-
quence (IMU placed on the left side).
Activity Recall Precision
(%) (%)
Running 100 89
Walking 99 88
Standing 92 100
Sitting 100 100
Lying 100 96
Jump 34 100
Fall 59 82
Table 3: Recall and precision results reported by (Frank
et al., 2010).
Activity Recall Precision
(%) (%)
Running 93 100
Walking 100 98
Standing 98 100
Sitting 100 97
Lying 98 96
Jump 93 93
Fall 100 80
more accurately, the models for a sensor on the right.
In the case of Sinja, the sensor was on the left side.
Nevertheless, the results achieved are considered ac-
ceptable.
This model also gives interesting information in
terms of intra-activity dynamics. Figure 6 shows the
acceleration signals in the x-, y- and z-axes (acc
x
, acc
y
and acc
z
, respectively) and the events inferred during
the activity of walking. The rhythmic transitions be-
tween events, E
W lk
2
and E
W lk
3
, are seen to correspond
with the stepping pattern in the acceleration signals.
So, not only has the definition of the hierarchical dy-
namic model proposed in this work allowed accurate
classification of activities without preprocessing of
the raw sensor signals, but the information regarding
the dynamics within the activity itself could also be
used to further characterise the subject’s motion pat-
58 59 60 61 62 63
−15
−10
−5
0
5
10
Time (sec)
m/s
2
Walking
acc
x
acc
y
acc
z
E
2
Wlk
E
3
Wlk
Event sequence
Figure 6: Events inferred for walking and acceleration sig-
nals.
terns and provide useful contextual awareness for the
monitoring system.
Parameterisation of the intra-activity dynamics,
inferred for a particular subject, might have potential
applications in areas such as gait analysis for rehabili-
tation science. However, to be truly useful in this type
of application, it would likely be necessary to improve
the level of detail, by implementing, for example, a
model with a variable number of intermediate states.
7 CONCLUSIONS AND FUTURE
WORK
This work has proposed a new approach to the task
of human daily activity recognition using wearable
inertial sensors. The method presented has two dy-
namic levels, augmenting the information provided
by activity classification alone, through the provision
of supplementary information regarding the dynamics
within the activity.
Additionally, our method bypasses the typically
used feature extraction process, which is a computa-
tional bottleneck in current activity recognition meth-
ods. Working directly with the raw signals from the
IMU sampled at a low sampling rate, the inherent dy-
namic nature of human motion is exploited. With this
novel method, results with high precision and recall
rates have been obtained.
Future research plans include developing more so-
phisticated models to take into account variations in
sensor placement as well as implementing the algo-
rithm in real-time. Moreover, a system to extract fea-
tures and parameters from the intra-activity dynam-
ics, provided among the outputs of the new algorithm,
will be developed, to facilitate a detailed analysis of
HIERARCHICAL DYNAMIC MODEL FOR HUMAN DAILY ACTIVITY RECOGNITION
67

human behaviour in context-aware monitoring sys-
tems.
ACKNOWLEDGEMENTS
This work has been partly supported by Ministe-
rio de Educaci
´
on of Spain (projects ‘DEIPRO’, id.
TEC2009-14504-C02-01, and ‘COMONSENS’, id.
CSD2008-00010).
REFERENCES
Altun, K. and Barshan, B. (2010). Human activity recog-
nition using inertial/magnetic sensor units. In Pro-
ceedings of the First International Conference on Hu-
man Behavior Understanding, HBU’10, pages 38–51,
Berlin, Heidelberg. Springer-Verlag.
Bao, L. and Intille, S. S. (2004). Activity Recognition from
User-Annotated Acceleration Data. Pervasive Com-
puting, pages 1–17.
Frank, K., Nadales, M. J. V., Robertson, P., and Angermann,
M. (2010). Reliable real-time recognition of motion
related human activities using MEMS inertial sensors.
In ION GNSS 2010.
Han, C. W., Kang, S. J., and Kim, N. S. (2010). Imple-
mentation of HMM-based human activity recognition
using single triaxial accelerometers. IEICE Transac-
tions, 93-A:1379–1383.
He, Z. Y. and Jin, L. W. (2008). Activity recognition from
acceleration data using AR model representation and
SVM. Machine Learning and Cybernetics.
Khan, A. M., Lee, Y.-K., Lee, S. Y., and Kim, T.-
S. (2010). A triaxial accelerometer-based physical-
activity recognition via augmented-signal features and
a hierarchical recognizer. IEEE Transactions on Infor-
mation Technology in Biomedicine, 14:1166–1172.
Krishnan, N. C., Colbry, D., Juillard, C., and Panchanathan,
S. (2008). Real time human activity recognition us-
ing tri-axial accelerometers. In Sensors Signals and
Information Processing Workshop (SENSIP).
Moeslund, T. B., Hilton, A., and Kr
¨
uger, V. (2006). A sur-
vey of advances in vision-based human motion cap-
ture and analysis. Computer Vision and Image Under-
standing, 104:90–126.
Oliver, N., Horvitz, E., and Garg, A. (2002). Layered rep-
resentations for human activity recognition. In Pro-
ceedings of the 4th IEEE International Conference on
Multimodal Interfaces, ICMI ’02, pages 3–, Washing-
ton, DC, USA. IEEE Computer Society.
Powell, H., Hanson, M., and Lach, J. (2007). A wearable
inertial sensing technology for clinical assessment of
tremor. In IEEE Biomedical Circuits and Systems
Conference, BIOCAS 2007., pages 9 –12.
Preece, S. J., Goulermas, J. Y., Kenney, L. P. J., and
Howard, D. (2009). A comparison of feature extrac-
tion methods for the classification of dynamic activi-
ties from accelerometer data. IEEE Transactions on
Biomedical Engineering, 56(3):871–879.
Rabiner, L. and Juang, B.-H. (1993). Fundamentals of
Speech Recognition. Prentice Hall, united states ed
edition.
Rabiner, L. R. (1990). Readings in speech recognition. In
Waibel, A. and Lee, K.-F., editors, Readings in speech
recognition, chapter A tutorial on hidden Markov
models and selected applications in speech recogni-
tion, pages 267–296. Morgan Kaufmann Publishers
Inc., San Francisco, CA, USA.
Sabatini, A., Martelloni, C., Scapellato, S., and Cavallo, F.
(2005). Assessment of walking features from foot in-
ertial sensing. IEEE Transactions on Biomedical En-
gineering, 52(3):486 –494.
Viterbi, A. (1967). Error bounds for convolutional codes
and an asymptotically optimum decoding algorithm.
IEEE Transactions on Information Theory, 13(2):260
– 269.
Winters, J. and Wang, Y. (2003). Wearable sensors and tel-
erehabilitation. IEEE Engineering in Medicine and
Biology Magazine, 22(3):56 –65.
Wu, G. and Xue, S. (2008). Portable preimpact fall de-
tector with inertial sensors. IEEE Transactions on
Neural Systems and Rehabilitation Engineering [see
also IEEE Trans. on Rehabilitation Engineering],
16(2):178–183.
Zhu, C. and Sheng, W. (2010). Recognizing human daily
activity using a single inertial sensor. In Proceedings
of the 8th World Congress on Intelligent Control and
Automation (WCICA), pages 282 –287.
BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing
68
