
MACHINE LEARNING OF HUMAN SLEEP PATTERNS
BASED ON STAGE BOUT DURATIONS
Francis W. Usher
1
, Chiying Wang
1
, Sergio A. Alvarez
2∗
, Carolina Ruiz
1
and Majaz Moonis
3
1
Department of Computer Science, Worcester Polytechnic Institute, Worcester, MA 01609, U.S.A.
2
Department of Computer Science, Boston College, Chestnut Hill, MA 02467, U.S.A.
3
Department of Neurology, U. of Massachusetts Medical School, Worcester, MA 01655, U.S.A.
Keywords:
Sleep, Bout duration, Sleep dynamics, Data mining, Clustering, Machine learning.
Abstract:
This paper explores the discovery of patterns in human sleep data based on the duration statistics of continuous
bouts in individual sleep stages during a full night of sleep. Hypnograms from 244 patients are examined.
Stage bout durations are described in terms of the quartiles of their stage bout duration distributions, yielding
15 descriptive variables corresponding to wake after sleep onset, NREM stage 1, NREM stage 2, slow wave
sleep, and REM sleep. Unsupervised Expectation-Maximization clustering is employed to identify distinct
groups of hypnograms based on stage bout durations. Each group is shown to be characterized by bout duration
quartiles of specific sleep stages, the values of which differ significantly from those of other groups (p < 0.05).
Among other sleep-related and health-related variables, several are shown to be significantly different among
the bout duration groups found through clustering, while multivariate linear regression fails to yield good
predictive models based on the same bout duration variables used in the clustering analysis. This provides an
example of the successful use of machine learning to uncover naturally occurring dynamical patterns in sleep
data that can also provide sleep-based indicators of health.
1 INTRODUCTION
Sleep is a fascinating process that is not yet fully un-
derstood. Sleep in mammals has been thought to be
controlled by body-wide mechanisms, in order to en-
sure energy conservation and recovery, but it has also
been proposed that sleep may be an emergent prop-
erty of the networks of neurons in the brain (Krueger
et al., 2008). Sleep is known to play a key role in
memory consolidation (Diekelmann and Born, 2010).
The scientific study of sleep has long used a subdi-
vision of sleep into distinct stages detected through
electroencephalography (EEG), supplemented by the
measurement of other physiological signals (Loomis
et al., 1937) – a technique known as polysomnog-
raphy. A particular stage associated with dream-
ing, the so-called Rapid Eye Movement (REM) stage,
was subsequently identified (Aserinsky and Kleit-
man, 1953), (Dement and Kleitman, 1957), leading to
currently used staging standards (Rechtschaffen and
Kales, 1968), (Iber et al., 2007) that comprise the light
sleep non-REM (NREM) stages NREM 1 and NREM
∗
Corresponding author.
2, a deep sleep (also known as slow-wave sleep
(SWS)) stage or stages NREM 3/4, as well as REM
sleep. Neuroimaging techniques, including fMRI and
PET, have yielded specific information about brain
activity in different regions of the brain during each
of these sleep stages (Dang-Vu et al., 2010).
Sleep normally progresses through the various
stages during the course of a full night, albeit in a
manner that is not predictable in detail. A sample
diagram of the temporal progression of human sleep
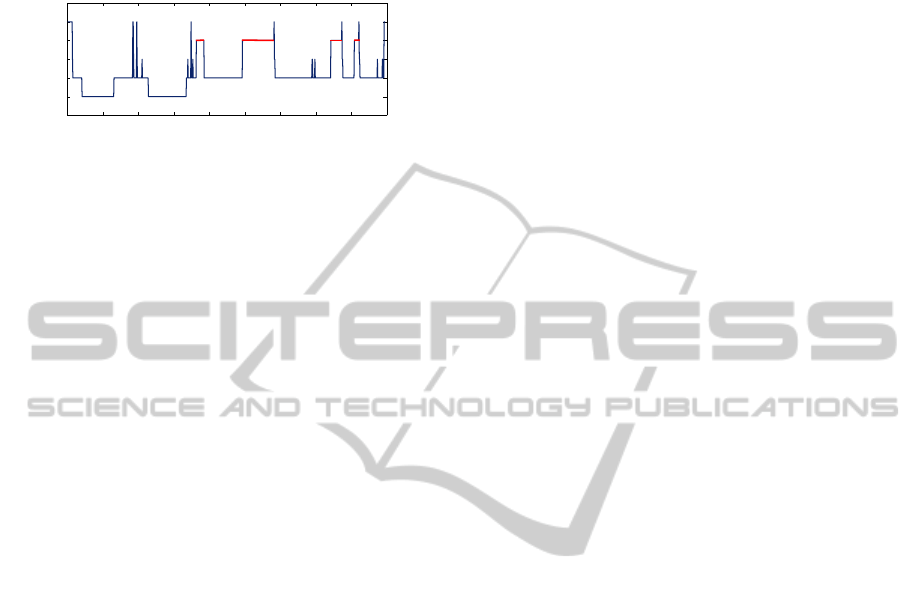
stages during the night, known as a hypnogram, is
shown in Fig. 1. This particular diagram was gen-
erated from one of the 244 polysomnographic record-
ings used in the present paper. Some typical features
to note are: most SWS (stages 3 and 4) occurs ear-
lier in the night, a greater amount of REM sleep oc-
curs later in the night, REM and stage 2 alternate
semi-cyclically, and there are brief periods of wake-
fulness throughout the night, after the initial onset of
sleep. Despite some common features across indi-
viduals, the detailed structure of sleep is known to
vary from person to person, and is affected by a va-
riety of factors, from such fundamental physical at-
tributes as body composition (Rao et al., 2009) and
71
W. Usher F., Wang C., A. Alvarez S., Ruiz C. and Moonis M..
MACHINE LEARNING OF HUMAN SLEEP PATTERNS BASED ON STAGE BOUT DURATIONS.
DOI: 10.5220/0003782500710080
In Proceedings of the International Conference on Health Informatics (HEALTHINF-2012), pages 71-80
ISBN: 978-989-8425-88-1
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
handedness (Propper et al., 2007), to behaviors such
as smoking (Zhang et al., 2006) and the practice of
yoga (Sulekha et al., 2006).
0 100 200 300 400 500 600 700 800 900
SWS
NREM 2
NREM 1
REM
wake
Time (epochs)
Sleep stage
Figure 1: Sample hypnogram from the present study.
Sleep structure is frequently described in terms of
sleep stage composition, that is, in terms of the col-
lection of percentages of time accounted for by var-
ious sleep stages within a night of sleep. For exam-
ple, see (Danker-Hopfe et al., 2005) and (Khasawneh
et al., 2011). While sleep stage composition provides
a good global summary of overall sleep stage content,
it does not capture any information about the dura-
tion and ordering of uninterrupted episodes of differ-
ent sleep stages during the night. Sleep stage dura-
tions havepreviouslybeen used to describe alterations
in sleep dynamics due to health status or ingested
neuroactive substances. For example, in (Bˇrezinov´a,
1976), it is shown that sleep stage durations are af-
fected in specific ways by age, caffeine, and hypnotic
drug withdrawal. Obstructive Sleep Apnea (OSA) is
shown to alter sleep stage dynamics in (Penzel et al.,
2003) and (Bianchi et al., 2010). Differences in mean
duration of stage 2 bouts between patients with fi-
bromyalgia and normal control subjects have been
described in (Burns et al., 2008). Exponential and
power-law functions have been proposed as models
for the stage duration distributions (Lo et al., 2002),
and the parameter values in these models have been
shown to be affected by health conditions such as
chronic fatigue syndrome (Kishi et al., 2008).
The work reported in the present paper uses a de-
scription of sleep dynamics based on the durations
of continuous, uninterrupted bouts in the different
sleep stages, as well as in wakefulness episodes af-
ter sleep onset. This representation captures tempo-
ral features of sleep that are not considered by stan-
dard sleep composition variables alone. In addition
to the durations of bouts in various sleep stages, it
would be desirable to account for the specific stage
to which a transition occurs at the end of each stage
bout. However, the information in a full night hypno-
gram appears to be insufficient to adequately model
such stage transitions (Bianchi et al., 2010). In
the present paper, the machine learning technique of
Expectation-Maximization (EM) clustering is used to
group hypnograms into families based on the distri-
butions of their stage bout durations. Hypnograms
within each family are more similar to one another, in
terms of their bout duration statistics, than are hypno-
grams from different families. The prior work (Kha-
sawneh et al., 2011) also uses clustering to study sleep
data, but considers only stage composition, not bout
durations nor other aspects of sleep dynamics. In the
work presented here, each family is shown to be char-
acterized by bout duration statistics for specific sleep
stages, the values of which are shown to be statisti-
cally significantly different from those of other fam-
ilies at the level p < 0.05, even after a suitable cor-
rection has been made for the magnification of type
I error due to multiple statistical comparisons. Fur-
thermore, several potentially health-related variables
which do not enter into the definition of the bout du-
ration families, such as a sensation of muscle weak-
ness or paralysis that occurs in emotional situations,
are also shown to differ significantly among the bout
duration families identified through machine learn-
ing, at the level p < 0.05. This is particularly note-
worthy because, in contrast to machine learning, the
widely used statistical technique of multivariate linear
regression does not provide a good predictive model
of this muscle paralysis variable based on the same
bout duration variables. Our results show that ma-
chine learning can uncover interesting dynamical pat-
terns in sleep data, and that such patterns may also be
used to predict selected aspects of individual patient
health based on an all-night sleep study.
2 METHODS
2.1 Human Sleep Data
Fully anonymized human polysomnographic record-
ings were obtained from the Sleep Clinic at Day
Kimball Hospital in Putnam, Connecticut, USA. A
total of 244 recordings were used for the work re-
ported here. Summary statistics for this collection
of sleep data are as in Table 1. The acronyms that
appear in the header row of Table 1 have the fol-
lowing meanings. BMI: Body-Mass Index, the ra-
tio of body weight to height-squared; ESS: Epworth
Sleepiness Scale (Johns, 1991), a measure of day-
time sleepiness based on responses to a questionnaire;
BDI: Beck Depression Inventory(Storch et al., 2004),
a questionnaire-based measure of affective depres-
sion; Mean SaO
2
: mean level of oxygen-saturated
hemoglobin in the blood.
HEALTHINF 2012 - International Conference on Health Informatics
72
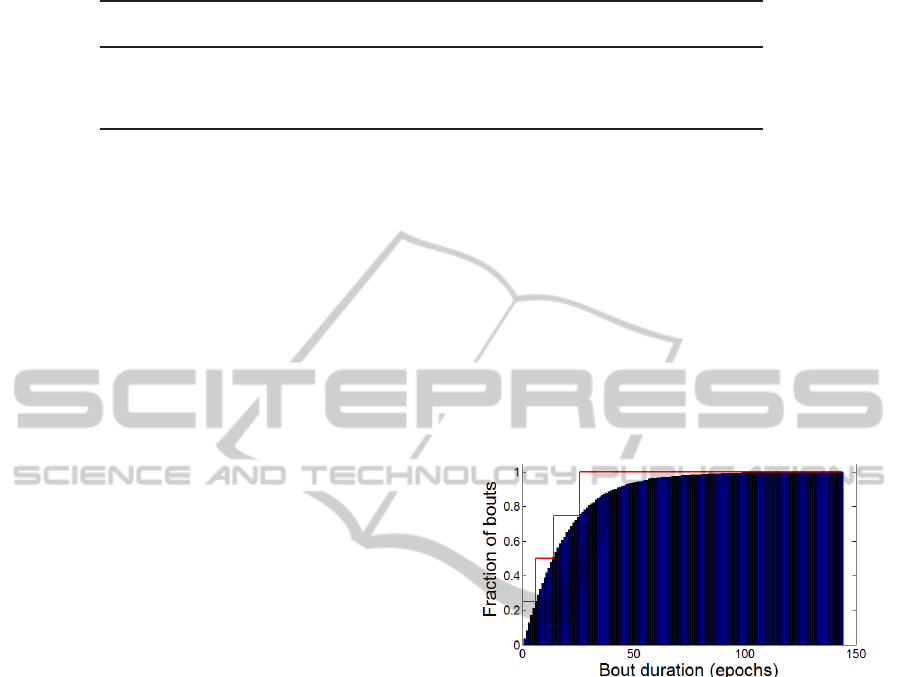
Table 1: Summary statistics of sleep dataset.
Age BMI ESS BDI Mean SaO
2
Heart rate
(years) (kgm
−2
) (score) (score) (%) (bpm)
Male (n=122) µ± σ 47.4±15.1 33.7±8.1 7.6±5.4 11.5±8.8 93.5±2.9 68.5±11.3
Female (n=122) µ± σ 48.4±14.5 33.7±8.3 7.1±4.8 13.0±7.8 94.6± 1.9 70.8±9.6
Overall (n=244) µ± σ 47.9±14.8 33.7±8.2 7.4±5.1 12.2±8.3 94.1±2.5 69.7±10.5
min–max 20–85 19.2–64.6 0–23 0–48 70.2–97.9 46–99
2.2 Descriptive Data Features
2.2.1 Staging
The polysomnographic recordings were staged in
30-second epochs by expert sleep technicians fol-
lowing the Rechtschaffen and Kales (R & K) stan-
dard (Rechtschaffen and Kales, 1968). R & K NREM
stages 3 and 4 were then combined to obtain a single
slow wave sleep (SWS) stage, resulting in stage labels
that are known (Moser et al., 2009) to provide a good
approximation to the more recently proposed AASM
staging standard (Iber et al., 2007).
2.2.2 Sleep Stage Bouts and Bout Durations
Next, bout durations in epochs were extracted from
each hypnogram. A bout is defined to be a maxi-
mal uninterrupted segment of the given stage within
a given hypnogram. For example, four distinct REM
bouts are visible in Fig. 1. A bout that begins in epoch
t has duration T − t, where T is the first epoch after t
such that the sleep stages of the given hypnogram in
epochs t and T are not the same.
2.2.3 Cumulative Distribution Function
The cumulative distribution function (CDF) of the
bout durations was then computed for each sleep
stage. The CDF of stage X is the function F
X
defined
for each duration, d, as follows (the letter P denotes
probability):
F
X
(d) = P(a bout of stage X has duration ≤ d)
With an average of 250 possible bout durations per
stage, this process yields a feature vector of length
approximately 1250 for each data instance.
2.2.4 Bout Duration Quartiles
Selected features of the duration distributions were
used to reduce the dimensionality of the data rep-
resentation. Specifically, only the three bout dura-
tion quartile values were used to describe each stage,
yielding a 15-dimensional feature vector for each in-
stance. For each stage X, and each index i = 1, 2, 3,
the i-th quartile X.Qi is defined as follows:
X.Qi = argmin
d
{F
X
(d) ≥ 0.25i},
where F
X
is the CDF of stage X. In words, the value
of X.Qi for a given set of hypnograms is the smallest
d for which at least i quarters of the stage X bouts in
the input set have a duration of d or less. As an illus-
tration, the CDF of NREM stage 2 bout durations for
the entire set of 244 hypnograms is shown in Fig. 2,
together with the compressed quartile representation,
visualized as a piecewise constant approximationwith
jumps at the quartile durations.
Figure 2: Stage NREM 2 bout duration CDF with quartiles
visualized as CDF approximation.
2.3 Clustering
2.3.1 Clustering Technique
Unsupervised clustering was applied to the set of 15-
dimensional feature vectors described in section 2.2
to seek objectively defined groups of hypnograms as-
sociated with distinct bout duration distributions. The
technique of Expectation-Maximization (EM) clus-
tering was selected after an experimental comparison
with k-means clustering showed higher stability of the
EM clustering results with respect to pseudorandom
initial parameter variation (see section 3.1). EM per-
forms iterative maximum likelihood estimation of the
cluster parameters (Dempster et al., 1977; Neal and
Hinton, 1998). Clustering experiments were carried
out using the Weka data mining toolkit (Hall et al.,
2009). A mixture of Gaussians is used as the cluster
model, and initial parameter values are found through
k-means clustering.
MACHINE LEARNING OF HUMAN SLEEP PATTERNS BASED ON STAGE BOUT DURATIONS
73

2.3.2 Measuring Clustering Stability
Stability of clustering results in the presence of pseu-
dorandom parameter initialization was assessed by
comparing the clusters that result from all pairs of 50
seed values for a given value of k. A measure of clus-
tering agreement based on the fraction of pairs of in-
stances that are grouped together in the same cluster
by each of the two clusterings, known as the adjusted
Rand Index (Hubert and Arabie, 1985), was computed
for all pairs of seed values. As compared with the
standard Rand Index (Rand, 1971), the adjusted Rand
Index is much more strict, as it accounts for the de-
gree of matching expected by chance. Subsequent ex-
periments were performed with a clustering of max-
imum mean adjusted Rand Index when compared to
the other 49 tested seed values.
2.4 Statistical Significance
Tests of statistical significance are employed here to
ensure validity of the findings at the level p < 0.05,
minimizing the inference of apparent patterns that
may occur due to chance. Specific statistical hypoth-
esis tests used are described below, together with the
methodology employed to control the type I error rate
due to multiple statistical comparisons.
2.4.1 Multiway and Pairwise Comparisons
When comparing means or medians of several popu-
lations (e.g., clusters), ANOVA or a Kruskal-Wallis
test are used. Likewise, statistical significance of
differences of means or medians between pairs of
populations is tested by using either a t-test or
Wilcoxon rank sum test, respectively. ANOVA and
t-tests presuppose normality of the distribution of the
means, a condition that may not hold exactly in all
cases. Nearly all of the comparisons performed in the
present paper involve populations with several dozen
members, and the normality condition is satisfied ap-
proximately. In any case, the Kruskal-Wallis and
Wilcoxon rank sum tests do not presuppose normality,
and provide additional confidence regarding statisti-
cal validity. A two-sample Kolmogorov-Smirnov test
is used to compare probabililty distributions without
any assumptions of a particular functional form, and
without targeting any particular statistic such as the
mean or median.
2.4.2 Correction for Increased Type I Error due
to Multiple Comparisons
Several of the results described are obtained through
exploratory data analysis, involving the simultaneous
testing of multiple statistical hypotheses. In any such
situation, the risk of a type I inference error – incor-
rectly rejecting a null hypothesis – increases due to
the accumulation of error over multiple comparisons.
This issue is addressed in the present paper using the
method of (Benjamini and Hochberg, 1995), which
provides rigorous control of the false discovery rate,
that is, of the expected proportion of multiple null hy-
potheses that are incorrectly rejected due to multiple
comparisons. Control of the false discovery rate is
performed at the significance level p < 0.05.
3 RESULTS
3.1 Clustering Stability
Table 2 contains the mean observed values of the ad-
justed Rand Index (see subsection 2.3) for EM and k-
means clustering, and k = 2, 3, 4. As shown, the mean
observed value of the adjusted Rand Index for EM is
at least 0.87 for all values of k considered. We note
that the values of the standard Rand Indexfor EM (not
shown) are at least 0.94 over the range k = 2, 3, 4.
The adjusted Rand Index accounts for the degree
of matching expected by chance, and thus produces
more conservative values. The high values obtained
for the adjusted Rand Index show that the EM cluster-
ing obtained is only slightly influenced by the initial
parameter values, and represents a stable grouping of
the hypnograms. Furthermore, EM consistently out-
performs k-means as regards clustering stability over
the stage bout duration dataset. For this reason, EM
was selected as the clustering algorithm for the work
discussed in the present paper. The seed value 8 was
found to provide an EM clustering of maximum mean
adjusted Rand Index as compared to the other 49 seed
values considered, for each k = 2, 3, 4. All results dis-
cussed subsequently in this paper utilize the EM clus-
tering resulting from the seed value 8.
In passing, we note that variants of the bout du-
ration quartile data representation described in sec-
tion 2.2.4, but using more than 4 quantiles, were also
considered for the present work. The advantage of us-
ing a greater number of quantiles is the ability to de-
scribe finer details in the bout duration distributions.
However, clustering stability was considerably lower
with such representations, and so the decision was
made to use quartiles only.
HEALTHINF 2012 - International Conference on Health Informatics
74
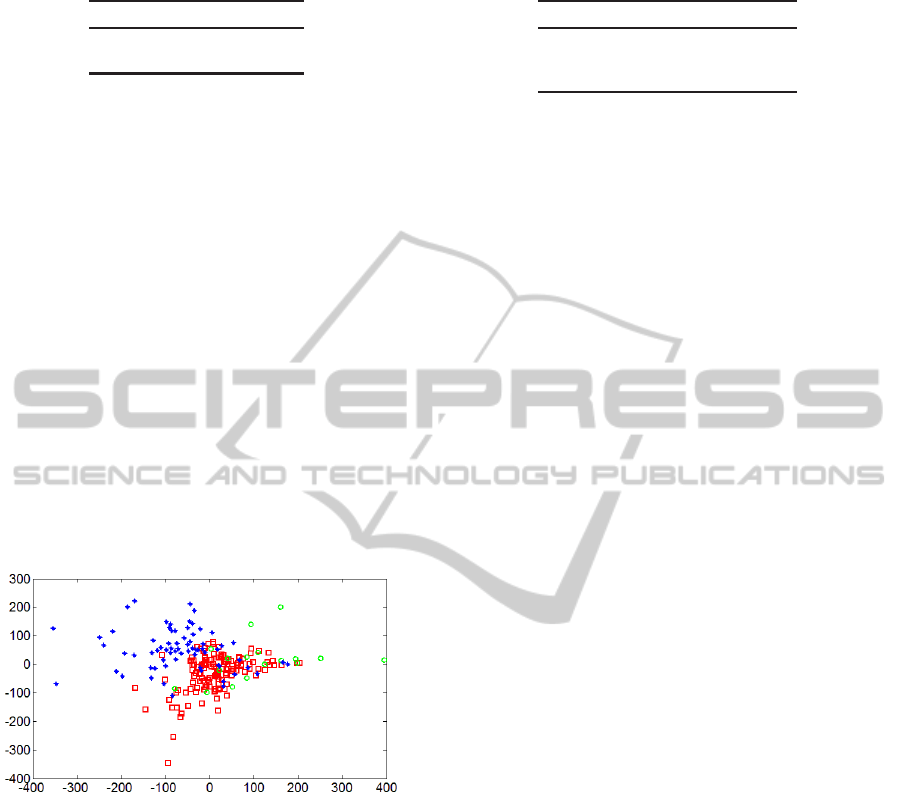
Table 2: Mean adjusted Rand Index stability values.
k 2 3 4
EM 0.99 0.90 0.87
k-means 0.51 0.53 0.36
3.2 Cluster Separation
3.2.1 Visualization of Cluster Separability
The visualization technique of multidimensional scal-
ing (MDS) provides a low-dimensionalnonlinear pro-
jection of a set of dataset in a way that minimizes
distortion of the distances between pairs of data in-
stances (Borg and Groenen, 2005). Fig. 3 shows a
two-dimensional MDS projection of the set of data
instances used in the present paper. The results of
EM clustering did not enter into the generation of the
MDS projection. The EM cluster labels for k = 3 were
used only to determine the glyph (marker) used for
each instance in the visualization shown. The MDS
result shows only moderate separation among the EM
clusters in two dimensions, which indicates that more
than two variables are likely to be needed in order to
achieve high separation. See section 3.2.2.
Figure 3: Multidimensional scaling cluster visualization.
3.2.2 Measurement of Cluster Separation via
Classification
Separation among clusters was further assessed quan-
titatively by performing a classification task in which
the EM cluster labels are viewed as the target class
attribute, with the variables used for clustering used
as predictive attributes. Classification accuracy, the
fraction of instances for which the cluster label is cor-
rectly predicted, and the area under the Receiving Op-
erating Characteristic (ROC) plot (Fawcett, 2003), re-
main consistently above 0.80 in the cases k = 2, 3, 4
for widely used classification techniques including
C4.5 (J48) decision tree learning, na¨ıve Bayes, and
multilayer artificial neural networks (ANN). The area
under the ROC plot accounts for prediction errors on
Table 3: Area Under ROC Graph for Selected Classifiers.
classifier k = 2 k = 3 k = 4
ANN 0.94 0.97 0.91
J48 0.88 0.90 0.89
naive Bayes 0.99 0.98 0.98
a per-class basis, and is a better measure of classifi-
cation performance in this context because the class
(cluster) sizes are very dissimilar. Accuracy can
produce overly optimistic results in such situations.
Mean values of the area under the ROC plot for se-
lected classifiers appear in Table 3. A 4-fold cross-
validation protocol was employed to control variance
due to data sampling.
Cluster separation is at best moderate in two-
dimensional projections of the bout duration dataset
in terms of the bout duration clustering variables, as
expected based on the MDS visualization in Fig. 3.
An example of moderate cluster separation occurs
with the wake.Q3 and SWS.Q1 bout duration quartile
variables. Use of the rule induction algorithm RIP-
PER (Cohen, 1995) (JRIP) over these predictive vari-
ables alone, with the k = 3 cluster label as the class,
yields, after pruning and simplification, the classifica-
tion rules shown in Fig. 4. The final rule is a default
rule that is used when the other rules do not apply.
This particular model attains an accuracy of 0.77 and
a mean area under the ROC plot of 0.76. Although the
classification performance of the model in Fig. 4 is
unremarkable, it provides an easily understood rough
description of the clusters in the case k = 3. In partic-
ular, it suggests that cluster 2 is associated with high
wake bout durations. More detailed characterizations
of the various clusters are discussed in section 3.3.4.
3.3 Statistical Properties of the Bout
Duration Clusters
3.3.1 Cluster Sizes and Membership
The sizes of the EM bout duration clusters for k =
2, 3, 4 appear in Table 4. There exist relationships
among the three families of clusterings, each of which
corresponds to a value of k in the range 2, 3, 4. These
relationships are observed by examining the detailed
lists of individual instances (not shown) that comprise
the various clusters. A simplified description of the
relationships among clusterings for different values of
k is the following. Additional characteristics of indi-
vidual clusters are given in Table 5 and discussed in
section 3.3.4.
Relationships between k = 2 and k = 3 Clusters.
The cluster labeled 1 in the k = 2 family splits into
MACHINE LEARNING OF HUMAN SLEEP PATTERNS BASED ON STAGE BOUT DURATIONS
75

(wake.Q3 >= 50) => cluster=cluster2 (10.0/0.0)
(SWS.Q1 >= 30) => cluster=cluster3 (41.0/2.0)
(SWS.Q1 >= 17) and (6 >= wake.Q3 >= 4) => cluster=cluster3 (13.0/3.0)
=> cluster=cluster1 (180.0/37.0)
Figure 4: JRIP rule model of k = 3 clusters using wake.Q3 and SWS.Q1 only. Coverage/errors in parentheses.
Table 4: Sizes of the bout duration clusters.
k 2 3 4
{211, 33} {148, 19, 77} {127, 15, 48, 54}
the two k = 3 clusters labeled 1 and 3. As discussed
in section 3.3.4 below, the k = 3 cluster 3 portion is
characterized by higher SWS bout duration quartiles
than the k = 3 cluster 1 portion. Two-thirds of the
k = 2 cluster 2 – with higher wakeand lower SWS and
REM bout duration quartiles – retains its identity in
the k = 3 family; the remaining one-third of the k = 2
cluster 2 joins the k = 3 cluster 3. The only inaccuracy
in this description is that 3 of the 33 instances in the
k = 2 cluster 2 join the k = 3 cluster 1.
Relationships between k = 3 and k = 4 Clusters.
In the transition between k = 3 and k = 4, cluster 1
remains largely unchanged (with only 12 of 148 in-
stances leaving cluster 1 and joining cluster 4). Clus-
ter 2 remains mainly within cluster 2 (with 4 of 19
instances joining cluster 4, which has higher mean
REM bout duration quartiles than cluster 2; see sec-
tion 3.3.4). Two-thirds of the k = 3 cluster 3 joins
the k = 4 cluster 2, and the remaining one-third of
k = 3 cluster 3 remains within the k = 4 cluster 3 (8
instances join k = 4 cluster 4). However, the k = 4
cluster 3 retains the characteristic, shared with k = 3
cluster 3, of having the highest SWS bout duration
quartiles among clusters.
3.3.2 Cluster Bout Duration Summary Statistics
The mean, standard deviation, median, and mean ab-
solute deviation of the 15 descriptive variables were
computed for each of the EM clusters, with a view to-
ward establishing statistical differences among clus-
ters. Table 5 provides numerical values of the bout
duration quartile means of the different clusters for
k = 2, 3, 4. Fig. 5, 6, 7 show the mean values of the
15 clustering variables in the cases k = 2, 3, 4, respec-
tively. These figures suggest that each cluster is char-
acterized by different bout duration quartiles for one
or more of the sleep stages than the other clusters
(e.g., cluster 2 by higher wake duration quartiles).
3.3.3 Multiway Cluster Comparisons
Statistical significance of the observed differences in
the means among clusters was assessed by ANOVA
and Kruskal-Wallis tests for multiway comparisons,
and by t, and Wilcoxon rank sum tests for pair-
wise comparisons. A nonparametric two-sample
Kolmogorov-Smirnovtest was also used to determine
differences between pairs of clusters in the overall
distributions of the bout duration quartile variables.
All p-values were corrected for multiple compar-
isons using the Benjamini-Hochberg method on a per
clustering basis, so that reported p-values are upper
bounds on the false discovery rate relative to all find-
ings over the given family of k clusters. The results
are as follows. For all clustering families, k = 2, 3, 4,
the wake stage and stage NREM1 duration quartile
variables differ significantly among clusters in a mul-
tiway comparison using the Kruskal-Wallis test (p <
0.05). ANOVA results are in agreement with Kruskal-
Wallis, with the exception that the inter-cluster differ-
ence in the quartile variable REM.Q1 is not found to
be significant for k = 2, 3. Additionally, both Kruskal-
Wallis and ANOVA find highly significant (p < 10
−6
)
differences among clusters in the SWS bout duration
quartile variables for k = 3, 4. In contrast, the dif-
ferences in the stage NREM2 bout duration quartiles
among clusters are not found to be significant for any
of the clustering families, k = 2, 3, 4. Pairwise statis-
tical comparisons provide additional information, and
are discussed in section 3.3.4 below.
3.3.4 Pairwise Comparisons. Bout Duration
Characteristics of Individual Clusters
The following are a few noteworthy statistically sig-
nificant differences in bout durations. The reader is
also referred to Table 5, and Fig. 5, 6, 7 in conjunction
with this discussion. Below, the precise family (value
of k) is sometimes omitted, in case in which bout du-
ration characteristics of a particular cluster number
are qualitatively similar for different values of k.
Cluster 1. Clusters 1 and 3 share the property that
their median wake bout duration quartiles are sig-
nificantly lower than for clusters 2 and 4 (Wilcoxon
p < 0.05). On the other hand, cluster 1 has signifi-
cantly lower SWS bout duration quartiles than clus-
HEALTHINF 2012 - International Conference on Health Informatics
76
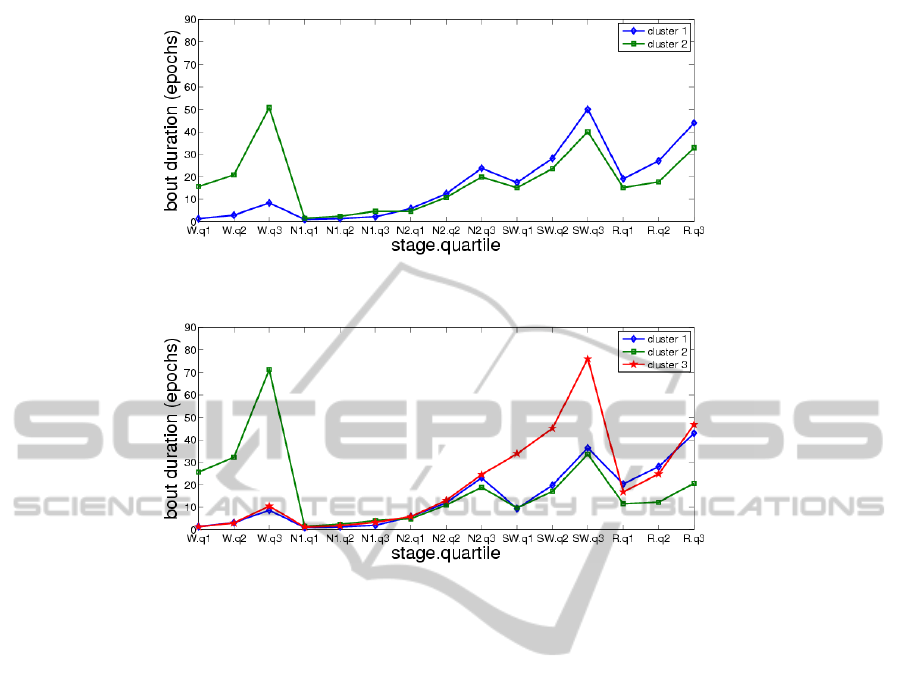
Figure 5: Mean values of clustering variables, k = 2.
Figure 6: Mean values of clustering variables, k = 3.
ter 3. See Fig. 5, Fig. 6, and Fig. 7. The bout dura-
tion characteristics of cluster 1 are remarkably stable
across values of k.
Cluster 2. Cluster 2 consistently has significantly
higher wake bout duration quartiles than any other
cluster, for k = 2, 3, 4 (Wilcoxon p < 0.02). The
single exception is the variable wake.Q1 in the case
k = 4. Low sample sizes for k = 4 clusters 2 and 4
(15 and 24, respectively) likely contribute to the latter
isolated nonsignificance finding. One also observes
that, in the progression from k = 2 to k = 3 to k = 4,
cluster 2 has monotonically decreasing REM bout du-
ration quartiles.
Cluster 3. As observed in section 3.3.1, 145 of the
148 instances (approximately 98%) in the k = 3 ver-
sion of cluster 3 belong to the k = 2 version of cluster
1. The remainder of the k = 2 cluster 1 instances form
the majority of the k = 3 cluster 3. Therefore, it is not
surprising that many of the bout duration quartiles for
the k = 3 version of cluster 3 are similar to those for
cluster 1. See Fig. 6 and Table 5. However, there is an
immediately noticeable difference between clusters 1
and 3 for k = 3, namely the fact that cluster 3 has vis-
ibly higher SWS bout duration quartiles than all other
clusters, including cluster 1. In other words, cluster
3 for k = 3 consists mainly of those k = 2 cluster 1
instances with higher SWS bout duration quartiles.
This high SWS bout duration description of cluster 3
persists for k = 4. However, the observed SWS quar-
tile bout durationsfor cluster 3, though highest among
all clusters, are not significantly higher than those of
clusters 2 and 4, again due likely to the small sizes of
the latter clusters.
Cluster 4. Cluster 4 is characterized by signifi-
cantly higher REM bout quartile durations than any
other cluster (Wilcoxon p < 10
−3
).
Clustering Description via Classification Rules.
One can compare the characterizations of the clusters
described in the preceding paragraphs with the model
constructed by the JRIP conjunctive rule classifier in
the case k = 3. The model is as shown in Fig. 8, and
achieves a classification accuracy of 0.86 and mean
ROC area of 0.88. The rules of this model closely
agree with the descriptions provided above.
MACHINE LEARNING OF HUMAN SLEEP PATTERNS BASED ON STAGE BOUT DURATIONS
77
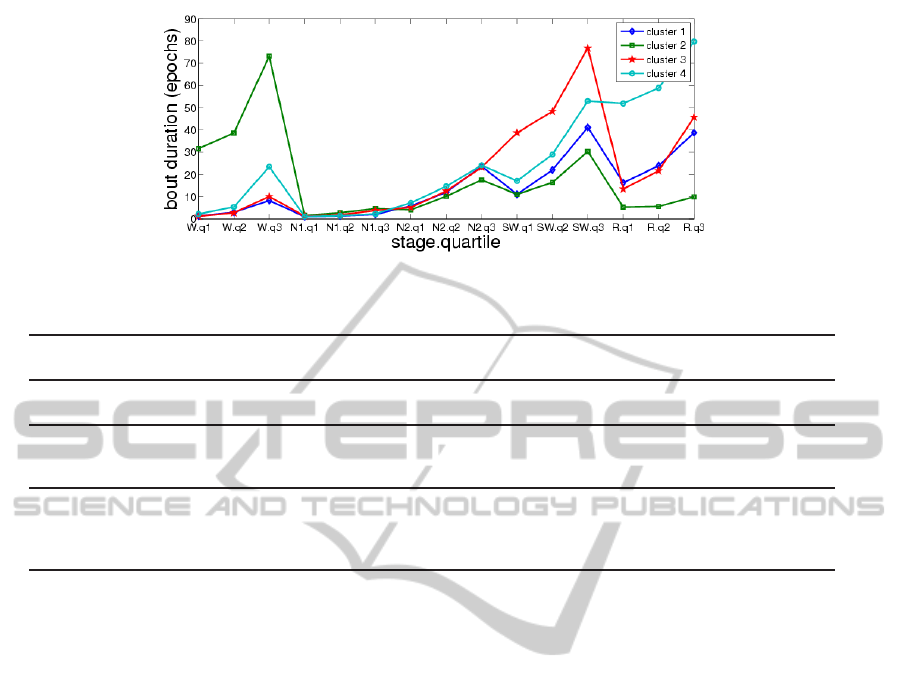
Figure 7: Mean values of clustering variables, k = 4.
Table 5: Mean bout duration quartiles of different clusters, in epochs.
wake N1 N2 SWS REM
Q1 Q2 Q3 Q1 Q2 Q3 Q1 Q2 Q3 Q1 Q2 Q3 Q1 Q2 Q3
k = 2 cluster 1 (n=211) 1.4 2.9 8.4 1.1 1.4 2.2 5.9 12 24 17 28 50 19 27 44
k = 2 cluster 2 (n=33) 16 21 51 1.5 2.5 4.6 4.6 11 20 15 24 40 15 18 33
k = 3 cluster 1 (n=148) 1.5 3.1 8.6 1.0 1.3 2.0 5.8 12 23 9.4 20 36 20 28 43
k = 3 cluster 2 (n=19) 26 32 71 1.5 2.5 4.1 4.8 11 19 9.7 17 34 12 12 21
k = 3 cluster 3 (n=77) 1.4 3 10 1.2 1.8 3.3 5.8 13 25 34 45 76 17 25 47
k = 4 cluster 1 (n=157) 1.4 3.0 8.2 1.1 1.4 2.1 5.8 12.0 24 11 22 41 16 24 39
k = 4 cluster 2 (n=15) 32 39 73 1.6 2.7 4.6 4.1 10 18 11 16 30 5.3 5.6 9.9
k = 4 cluster 3 (n=48) 1.3 2.8 10 1.2 1.9 3.7 5.1 13 23 39 48 77 13 22 46
k = 4 cluster 4 (n=24) 2.2 5.4 23 1.1 1.5 2.3 7.2 15 24 17 29 53 52 59 80
3.4 Health-related Cluster Differences
3.4.1 Comparisons of Sleep-related and
Health-related Variables
The boutduration clusters identified by the EM proce-
dure were examined to determine differences among
them in the values of sleep-related and health-related
variables not used in the clustering procedure itself.
Group comparisons of means and medians were per-
formed using ANOVA and Kruskal-Wallis tests, re-
spectively. Pairwise comparisons of means and medi-
ans used a t-test and Wilcoxon rank sum test. For all
values of k = 2, 3, 4, Kruskal-Wallis and ANOVA de-
termined that mean sleep latency (time elapsed from
getting in bed until first non-wake epoch) differs sig-
nificantly among bout duration clusters (p < 0.05).
The highest mean value of sleep latency occurs in
cluster 2. The pairwise difference in mean and median
sleep latency between cluster 2 and all other clusters
is also significant (p < 0.05). As observed in Table 5
and discussed in section 3.3.4, cluster 2 has the high-
est mean wake bout duration quartiles of all of the
clusters. It is entirely possible that the high sleep la-
tency contributesto the increased wake bout durations
in cluster 2. Certain variables that correspond to indi-
vidual items in the EpworthDaytime Sleepiness ques-
tionnaire are also significantly different in a multi-
way comparison among clusters, and are significantly
different in pairwise comparisons between cluster 2
and the others in particular: a sensation of muscular
weakness or paralysis during laughter, anger, or emo-
tional situations, and the recollection of vivid dreams
and nightmares, differ significantly among clusters
for k = 2, 3, and are highest in cluster 2 for k = 2, 3
(p < 0.05); an uncomfortable crawly sensation in the
legs that is relieved by walking differs significantly
(p < 0.05) among clusters for k = 3, 4, and is lowest
in cluster 2.
3.4.2 Comparison with Multivariate Linear
Regression
Based on the finding of significant differences in
health variables in section 3.4.1, it is natural to ask
whether standard linear regression can provide good
predictions of one of these variables, such as a muscle
weakness or paralysis in emotional situations, based
on bout duration statistics. In the case k = 3, least
squares linear regression yields the model in Fig. 9
(coefficients shown to two significant digits).
Terms involving wake bout duration quartiles,
which as discussed in section 3.3.3 differentiate clus-
ter 2 from the others, and in which paralysis attains
its maximum value as discussed in section 3.4.1, ap-
pear in the regression model of Fig. 9. However,
HEALTHINF 2012 - International Conference on Health Informatics
78

(wake.Q3 >= 44) => cluster=cluster2 (12.0/1.0)
(wake.Q2 >= 6) and (SWS.Q1 <= 5) => cluster=cluster2 (5.0/1.0)
(NREM1.Q2 >= 3) and (NREM2.Q2 <= 9) => cluster=cluster2 (5.0/1.0)
(SWS.Q1 >= 30) => cluster=cluster3 (41.0/2.0)
(NREM1.Q3 >= 4) => cluster=cluster3 (22.0/1.0)
(SWS.Q3 >= 79) => cluster=cluster3 (15.0/3.0)
(SWS.Q2 >= 49) => cluster=cluster3 (5.0/2.0)
=> cluster=cluster1 (139.0/0.0)
Figure 8: JRIP conjunctive rule model of the clusters for k = 3.
paralysis =
-0.015 wake.Q1 + 0.012 wake.Q2 + 0.0037wake.Q3
-0.22 NREM1.Q1 + 0.07 NREM1.Q3
+0.03 NREM2.Q1 + 0.018 NREM2.Q2
-0.0045 REM.Q1 - 0.012
Figure 9: Least squares linear regression model of paralysis
(r
2
< 0.01).
the linear correlation between paralysis and the pre-
dictions of the least squares linear regression model
is less than 0.06. Thus, this model explains a frac-
tion that is less than 0.06
2
, which is much less than
1%, of the variance in paralysis. Nonlinear predic-
tive models obtained through regression based on the
machine learning technique of Support Vector Ma-
chines (SVM) provide slightly improvedperformance
here. In any case, the fact that paralysis differs sig-
nificantly among the bout duration-based groupings
found through clustering, already shows that machine
learning can uncover structure in health-related data
that is not clearly identified by more traditional statis-
tical techniques such as linear regression.
4 CONCLUSIONS AND FUTURE
WORK
This paper has applied unsupervised machine learn-
ing to the discovery of patterns in human sleep data
based on the duration distributions of continuous
bouts in the various sleep stages. The results pre-
sented identify groups of hypnograms with distinct
bout duration properties. The differences in bout du-
rations amonggroups are shown to be statistically sig-
nificant (p < 0.05), even after a correction to prevent
increased type I error due to multiple comparisons.
Each group is characterized by bout duration features
for specific sleep stages, the values of which differ
significantly from those of other groups.
Several sleep-related and health-related variables
not used in the grouping procedure have been com-
pared across groups. Of these variables, several dis-
play significantly different statistics in different bout
duration groups, including sleep latency and sev-
eral variables corresponding to items on the Epworth
Daytime Sleepiness questionnaire, such as muscular
weakness or paralysis associated with emotional situ-
ations, the recollection of vivid dreams or nightmares,
and an uncomfortable “crawly” sensation in the legs
that is relieved by walking. It is found that these vari-
ables are significantly different in the bout duration
group characterized by the highest mean duration of
wake bouts. This finding provides a specific manner
in which sleep dynamics reflects the values of vari-
ables that are not specific to sleep. It is of interest to
further explore the importance within sleep medicine
of these bout duration groups in future work.
The results presented in this paper are based on a
highly compressed representation of the bout duration
distributions, utilizing only the three quartile values
of the cumulative bout duration distribution for each
sleep stage. It is possible that this compression limits
the capacity of the clustering technique to identify im-
portant dynamical features. Increasing the number of
quantiles provides greater representational accuracy,
but was found to also reduce stability of the cluster-
ing results. Future work should investigate alternative
representations of sleep dynamical information that
simultaneously provide important detail in the distri-
butions and stability of the machine learning results.
Additionally, the current work only considers the
duration of each bout in a given stage, without re-
gard for what stage occurs immediately afterwards.
It would be desirable to also consider the statistics of
specific stage transitions in future work. However, ac-
curate modeling of the sleep stage transition statistics
may require the use of multiple nights’ sleep data, or
ambulatory monitoring of key physiological signals.
REFERENCES
Aserinsky, E. and Kleitman, N. (1953). Regularly occurring
periods of eye motility, and concomitant phenomena,
during sleep. Science, 118(3062):273–274.
Benjamini, Y. and Hochberg, Y. (1995). Controlling the
false discovery rate: a practical and powerful ap-
proach to multiple testing. Journal of the Royal Sta-
tistical Society, Series B, 57(1):289–300.
Bianchi, M. T., Cash, S. S., Mietus, J., Peng, C.-K.,
and Thomas, R. (2010). Obstructive sleep apnea al-
MACHINE LEARNING OF HUMAN SLEEP PATTERNS BASED ON STAGE BOUT DURATIONS
79

ters sleep stage transition dynamics. PLoS ONE,
5(6):e11356.
Borg, I. and Groenen, P. J. F. (2005). Modern Multidimen-
sional Scaling: Theory and Applications (Springer
Series in Statistics). Springer, Berlin, 2nd edition.
Burns, J. W., Crofford, L. J., and Chervin, R. D. (2008).
Sleep stage dynamics in fibromyalgia patients and
controls. Sleep Medicine, 9(6):689–696.
Bˇrezinov´a, V. (1976). Duration of EEG sleep stages in dif-
ferent types of disturbed night sleep. Postgrad Med J.,
52(603):3436.
Cohen, W. W. (1995). Fast effective rule induction. In
Twelfth International Conference on Machine Learn-
ing, pages 115–123. Morgan Kaufmann.
Dang-Vu, T., Schabus, M., Desseilles, M., Sterpenich, V.,
Bonjean, M., and Maquet, P. (2010). Functional
neuroimaging insights into the physiology of human
sleep. Sleep, 33(12):1589–603.
Danker-Hopfe, H., Schfer, M., Dorn, H., Anderer, P.,
Saletu, B., Gruber, G., Zeitlhofer, J., Kunz, D., Bar-
banoj, M.-J., Himanen, S., Kemp, B., Penzel, T.,
Rschke, J., and Dorffner, G. (2005). Percentile refer-
ence charts for selected sleep parameters for 20- to 80-
year-old healthy subjects from the SIESTA database.
Somnologie - Schlafforschung und Schlafmedizin,
9:3–14. 10.1111/j.1439-054X.2004.00038.x.
Dement, W. and Kleitman, N. (1957). The relation of eye
movements during sleep to dream activity: An objec-
tive method for the study of dreaming. Journal of Ex-
perimental Psychology, 53:339–46.
Dempster, A. P., Laird, N. M., and Rubin, D. B. (1977).
Maximum likelihood from incomplete data via the
EM algorithm. Journal of the Royal Statistical So-
ciety, Series B, 39(1):1–38.
Diekelmann, S. and Born, J. (2010). The memory function
of sleep. Nat Rev Neurosci, 11(2):114–126.
Fawcett, T. (2003). ROC graphs: Notes and practical
considerations for data mining researchers. Hewlett-
Packard Labs Technical Report HPL-2003-4.
Hall, M., Frank, E., Holmes, G., Pfahringer, B., Reutemann,
P., and Witten, I. (2009). The WEKA data mining
software: an update. SIGKDD Explor., 11(1):10–18.
Hubert, L. and Arabie, P. (1985). Comparing par-
titions. Journal of Classification, 2:193–218.
10.1007/BF01908075.
Iber, C., Ancoli-Israel, S., Chesson, A., and Quan, S.
(2007). The AASM Manual for the Scoring of Sleep
and Associated Events: Rules, Terminology, and Tech-
nical Specifications. American Academy of Sleep
Medicine, Westchester, Illinois, USA.
Johns, M. W. (1991). A new method for measuring day-
time sleepiness: the epworth sleepiness scale. Sleep,
14(6):540–545.
Khasawneh, A., Alvarez, S. A., Ruiz, C., Misra, S., and
Moonis, M. (2011). EEG and ECG characteristics
of human sleep composition types. In Traver, V.,
Fred, A., Filipe, J., and Gamboa, H., editors, Proc.
HEALTHINF 2011, in conjunction with BIOSTEC
2011, pages 97–106. SciTePress.
Kishi, A., Struzik, Z., Natelson, B., Togo, F., and Ya-
mamoto, Y. (2008). Dynamics of sleep stage tran-
sitions in healthy humans and patients with chronic
fatigue syndrome. Am J Physiol Regul Integr Comp
Physiol., 294(6):R1980–7.
Krueger, J. M., Rector, D. M., Roy, S., Van Dongen, H.
P. A., Belenky, G., and Panksepp, J. (2008). Sleep as
a fundamental property of neuronal assemblies. Nat
Rev Neurosci, 9(12):910–919.
Lo, C.-C., Amaral, L. A. N., Havlin, S., Ivanov, P. C., Pen-
zel, T., Peter, J.-H., and Stanley, H. E. (2002). Dynam-
ics of sleep-wake transitions during sleep. Europhys.
Lett., 57(5):625–631.
Loomis, A., Harvey, E., and Hobart, G. (1937). Cerebral
states during sleep, as studied by human brain poten-
tials. J. Experimental Psychology, 21(2):127–144.
Moser, D., Anderer, P., Gruber, G., Parapatics, S., Loretz,
E., Boeck, M., Kloesch, G., Heller, E., Schmidt,
A., Danker-Hopfe, H., Saletu, B., Zeitlhofer, J., and
Dorffner, G. (2009). Sleep classification according to
AASM and Rechtschaffen & Kales: Effects on sleep
scoring parameters. Sleep, 32(2):139–149.
Neal, R. and Hinton, G. (1998). A view of the EM algo-
rithm that justifies incremental, sparse, and other vari-
ants. In Learning in Graphical Models, pages 355–
368. Kluwer Academic Publishers.
Penzel, T., Kantelhardt, J. W., Lo, C.-C., Voigt, K., and Vo-
gelmeier, C. F. (2003). Dynamics of heart rate and
sleep stages in normals and patients with sleep apnea.
Neuropsychopharmacology, 28(S1):S48–S53.
Propper, R., Christman, S., and Olejarz, S. (2007). Home-
recorded sleep architecture as a function of hand-
edness II: Consistent right- versus consistent left-
handers. J Nerv Ment Dis., 195(8):689–692.
Rand, W. M. (1971). Objective criteria for the evaluation of
clustering methods. Journal of the American Statisti-
cal Association, 66(336):846–850.
Rao, M., Blackwell, T., Redline, S., Stefanick, M., Ancoli-
Israel, S., and Stone, K. (2009). Association between
sleep architecture and measures of body composition.
Sleep, 32(4):483–90.
Rechtschaffen, A. and Kales, A., editors (1968). A Manual
of Standardized Terminology, Techniques, and Scor-
ing System for Sleep Stages of Human Subjects. US
Department of Health, Education, and Welfare Public
Health Service – NIH/NIND.
Storch, E. A., Roberti, J. W., and Roth, D. A. (2004). Factor
structure, concurrent validity, and internal consistency
of the Beck depression inventory–second edition in a
sample of college students. Depression and Anxiety,
19(3):187–189.
Sulekha, S., Thennarasu, K., Vedamurthachar, A., Raju,
T., and Kutty, B. (2006). Evaluation of sleep archi-
tecture in practitioners of Sudarshan Kriya yoga and
Vipassana meditation. Sleep and Biological Rhythms,
4(3):207–214.
Zhang, L., Samet, J., Caffo, B., and Punjabi, N. (2006).
Cigarette smoking and nocturnal sleep architecture.
Am J Epidemiol., 164(6):529–537.
HEALTHINF 2012 - International Conference on Health Informatics
80
