
CONTROLLER DESIGN FOR A STANCE-CONTROL
KNEE-ANKLE-FOOT ORTHOSIS BASED ON OPTIMIZATION
TECHNIQUES
S. H. HosseinNia
1
, F. Romero
2
, B. Vinagre
1
, F. J. Alonso
2
and I. Tejado
1
1
Dept. of Electrical, Electronic and Automation Engineering, University of Extremadura,
Avda de Elvas S/N, Badajoz, Spain
2
Dept. of Mechanical Engineering, Energetics and Materials, University of Extremadura,
Avda de Elvas S/N, Badajoz, Spain
Keywords:
Active Orthosis, Biomechanics, Muscle Modeling, Optimization, Optimal Control.
Abstract:
Design of active orthosis is a challenging problem from both the dynamic simulation and control points of
view. The redundancy problem of the simultaneous human-orthosis actuation is an interesting exercise to
solve concerning the analytical and computational cost effectiveness. The physiological static optimization
approach tries to solve the actuation sharing problem. Its objective is to quantify the contributions of muscles
and active orthosis to the net joint torques in order to select the proper actuator for the joint. Depending on
the disability of each patient, different controllers can be designed. As a matter of fact, the duration of the
gait cycle for each patient should be different. In this paper, a PI controller is designed whose parameters are
tuned by optimizing a cost function which takes into account the patients muscle power and the error of the
knee angle with the reference value. Moreover, the final time is obtained by minimizing the mean of integral
squared errors. The performance of the method is shown by designing the controller for three types of patients,
ordered from low to high disability. The objective of this work is to use optimal control techniques based on
physiological static optimization approach to the design of active orthosis and its control.
1 INTRODUCTION
Spinal cord injuries (SCI) cause paralysis of the lower
extremities because of the break of the connection be-
tween nervous central system and muscular units of
the lower body. According to the standard neurolog-
ical classification of the American Spinal Injury As-
sociation (ASIA), there are different SCI levels de-
pending on motor and sensory function to be pre-
served. The ASIA Impairment SCALE (AIS) range
them from A (complete SCI) to E (normal and sen-
sory function). This work focuses in the assistance
of incomplete SCI subjects with AIS level C or D.
Those patients have partially preserved motor func-
tion in the key lower limb muscle groups, and can
perform a low-speed and high-cost pathological gait
by using walking aids. The energy cost and aesthet-
ics of this walk can be performed by means of active
orthosis, requiring external actuation mechanisms to
assist the motion of the lower limb joints during gait
cycle. Considerable efforts have been focused on the
design and application of passive and active orthoses
to assist standing and walking of SCI individuals.
There is a great evolution between the first con-
trollable active, a patent by Filippi in 1942 (Filippi,
1942) of a hydraulically-actuated device for adding
power at the hip and knee joints, and the actual or-
thotic devices. Concerning the first, developed at the
University of Belgrade in the 60’s and 70’s by Vuko-
bratovich et al. (Vukobratovic et al., 1972), these
early devices to aid people with paraplegia resulting
from spinal cord injury were limited to predefined
motions and had limited success. Nowadays, orthotic
systems use predefined patterns of joint motions and
torques together with classical control techniques or
EMG-based control, with the aim of integrating the
human musculoskeletal system and the assisting de-
vice. There are different designs in the literature, see
for example the review of Dollar (Dollar and Herr,
2008). Nevertheless, few studies (Silva et al., 2010;
Kao et al., 2010) examine the moment joint patterns
of combined patient-orthosis systems. Moreover, the
number of studies testing these systems on handi-
capped subjects is paradoxically low when comparing
59
H. HosseinNia S., Romero F., Vinagre B., J. Alonso F. and Tejado I..
CONTROLLER DESIGN FOR A STANCE-CONTROL KNEE-ANKLE-FOOT ORTHOSIS BASED ON OPTIMIZATION TECHNIQUES.
DOI: 10.5220/0003783900590064
In Proceedings of the International Conference on Biomedical Electronics and Devices (BIODEVICES-2012), pages 59-64
ISBN: 978-989-8425-91-1
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

with the studies on able-bodied subjects wearing the
orthosis.
To assist the proper design of active orthoses for
incomplete SCI, it is necessary to quantify the simul-
taneous contributions of muscles and active orthosis
to the net joint torques of the human-orthosis system.
Simulation of walking in individuals with incomplete
SCI wearing an active orthosis is a challenging prob-
lem from both the analytical and the computational
points of view, due to the redundant nature of the
simultaneous actuation of the two systems. In this
work, the functional innervated muscles of SCI pa-
tients will be modeled as Hill-type actuators, while
the idle muscles will be represented by stiff and dis-
sipative elements that increment the passive moments
of the inactive joints. The orthosis will be consid-
ered as a set of external torques added to the an-
kles, knees and hips to obtain net joint torque patterns
similar to those of normal unassisted walking. Kao
(Kao et al., 2010) suggests that able-bodied subjects
aim for similar joint moment patterns when walking
with and without robotic assistance rather than sim-
ilar kinematic patterns. This is the fundamental hy-
pothesis of this approach to obtain muscular forces:
the combined actuation of the musculoskeletal system
of the SCI subject and the active orthosis produce net
joint moment patterns similar to those of normal unas-
sisted walking. The muscle-orthosis redundant actua-
tor problem was solved through a physiological static
optimization approach (Alonso et al., 2011). A com-
parison between cost functions and various sets of in-
nervated muscles can be found in this work. Based
on these results, as Font et al. explained in (Font-
Llagunes et al., 2011), the proper actuation can be se-
lected, but control techniques are required to achieve
a suitable gait.
The objective of this work is to design an opti-
mal controller based on the minimization of a cost
function that takes into account the patients muscle
power and the tracking error of the knee angle. For
the patients with less capability, the weigh of the mus-
cle power in the cost function will be chosen bigger
whereas for patients with more capability, this weigh
will be chosen smaller. Therefore, this controller will
consider a trade off between accuracy of knee move-
ment regarding to healthy human waking and muscle
power of each patient.
The rest of the paper is organized as follows. In
Section 2, musculoskeletal modeling is stated. In ad-
dition, in order to obtain the muscular power devel-
oped by each muscle during gait cycle, the optimiza-
tion approach proposed in Alonso et al. (Alonso et al.,
2011) is applied. Section 3 addresses the design of
the optimal controller. Finally, Section 4 includes the
main conclusions of this work.
2 MUSCULOSKELETAL
MODELING
In this section, the biomechanical model adopted to
obtain net joint torques for normal walking is pre-
sented, as well as the muscle models for the functional
(innervated) and partially denervated muscles of the
spinal cord injured subject.
2.1 Biomechanical Multibody Model
The biomechanical model used has 12 degrees of free-
dom. It consists of twelve rigid bodies linked with
revolute joints (see Fig. 1), and is constrained to move
in the sagittal plane. Each rigid body is characterized
by mass, length, moment of inertia about the center
of mass, and distance from the center of mass to the
proximal joint. The equations of motion of the biome-
chanical multi-body system can be written as:
M ¨q + Φ
T
q
λ = Q, (1)
where M is the global (human-orthosis) mass ma-
trix, Φ
T
q
is the Jacobian matrix of the constraint equa-
tions, ¨q is the acceleration vector, Q is the generalized
force vector and λ are the Lagrange multipliers. Us-
ing kinematic and anthropometric data in (1), the net
joint torques during a physical activity or motion and
the resultant force and moment due to body-ground
contact can be calculated.
Figure 1: (a) Biomechanical model of the human orthosis
system. (b) Muscle groups of the lower limbs: 1 - Iliopsoas,
2 - Rectus Femoris, 3 - Glutei, 4 - Hamstrings, 5 - Vasti, 6 -
Gastrocnemius, 7 - Tibialis Anterior, 8 - Soleus.
2.2 Muscle Modeling: Innervated and
Denervated Muscles
According to AIS, it is possible to define several lev-
els which indicate the severity of the injury from A
BIODEVICES 2012 - International Conference on Biomedical Electronics and Devices
60

(complete) to E (normal motor and sensory function).
In the design cases C and D, the motor function is
preserved below the neurological level (lowest seg-
ment where motor and sensory functions are normal),
being the difference between them the muscle activ-
ity grade of the key muscles. This grade ranges from
0 (total paralysis) to 5 (active movement, full range
of motion, normal resistance). As Alonso et al. pro-
posed in (Alonso et al., 2011), the weakness of the
denervated muscles is modeled through a weakness
factor p ∈ [0, 1] that limits the maximum activation of
this muscles.
Both innervated and denervated are modeled as
Hill-type actuators. The Hill-type muscle-tendon
model (Zajac, 1989; Winter, 1991) is shown in Fig. 2
(a) and 2 (b). It consists of a contractile element (CE)
that generates the force, a nonlinear parallel elastic
element (PE), representing the stiffness of the struc-
tures in parallel with muscle fibers, and a nonlinear
series elastic (SE) element that represents the stiffness
of the tendon which is serially attached to the muscle
and completes the muscletendon unit. The two dif-
ferential equations that govern the muscle dynamics
are:
˙a = h(u, a), (2)
˙
f
mt
= g(a, f
mt
,l
mt
,v
mt
). (3)
Equation (2) refers to the activation dynamics,
which relates the muscle excitation u from the cen-
tral nervous system (CNS) and the muscle activation
a ∈ [0,1]. On the other hand, equation (3) defines the
force-generation properties as a function of the mus-
cle tendon length l
mt
and velocity v
mt
. Activation dy-
namics is not considered for the purpose of this work.
If the pennation angle α is constant, in accordance
with Fig. 2 (b):
l
mt
= l
se
+ l
ce
cos(α), (4)
f
mt
= f
se
= ( f
ce
+ f
pe
)cos(α) ≈ f
ce
cos(α), (5)
where the force of the parallel elastic element is set to
zero (Ackermann, 2007; Ackermann and Schiehlen,
2006). The tendon (SE) can be modeled by a sim-
ple quadratic force-strain curve depending on tendon
stiffness as follows:
f
SE
=
0 if l
se
< l
ts
k
t
(l
se
− l
ts
)
2
if l
se
> l
ts
, (6)
where l
ts
is the tendon slack length and k
t
is the SE
stiffness, which is given by:
k
t
=
f
0
(ε
0
l
t
s)
2
, (7)
being ε
0
(3% to 5%) the strain occurring at the max-
imal isometric muscle force f
0
(Ackermann, 2007).
The force generated by the CE f
ce
is a function of the
activation a, its length l
ce
, and its contraction veloc-
ity v
ce
. The expression for the concentric contraction
(v
ce
< 0) reads as:
f
ce
f
0
= a
B
r
( f
iso
+ A
r
) − A
r
(B
r
−
˜v
N
ce
f
ac
)
B
r
−
˜v
N
ce
f
ac
, (8)
where ˜v
N
ce
= v
ce
/l
opt
ce
, A
r
= 0.41, B
r
= 0.52 and f
iso
=
f
iso
(w,l
opt
ce
,l
ce
), which corresponds to the muscle iso-
metric force relative to the maximal isometric muscle
force f
0
and f
ac
= min(1,3.33a).
The expression for the eccentric contraction (v
ce
>
0) depends on ˜v
N
ce
and f
iso
. The force-length-velocity
relationship is shown in Fig. 2 (c).
Figure 2: Muscle model: (a) Conceptual scheme. (b) Hill
model (Zajac, 1989). (c) Force-length-velocity model.
In order to quantify the muscle weakness, the
muscle activation will be multiplied by the men-
tioned weakness factor p, where p = 1 for innervated
muscles, 0 < p < 1 for partially denervated muscles
and p = 0 for totally denervated muscles (no activ-
ity). The atrophy of denervated muscles, as exposed
by Thomas and Grumbles (Thomas and Grumbles,
2005), depends on the elapsed time from the injury.
This atrophy increases the passive torques at the joint.
Several studies (Edrich et al., 2000; Lebiedowska and
Fisk, 1999; Amankwah et al., 2004) show that pas-
sive torques tend to be larger in pathological than
in healthy individuals. To take this fact into ac-
count stiff and dissipative elements are included into
the model using the definitions given in (Amankwah
et al., 2004). Fig. 3 shows the increment of the knee
torque due to pathological passive torque compared
with the torques in normal gait (obtained through in-
verse dynamics analysis from the 2D walking kine-
matic benchmark from Winter (Winter, 1991)). As
CONTROLLER DESIGN FOR A STANCE-CONTROL KNEE-ANKLE-FOOT ORTHOSIS BASED ON
OPTIMIZATION TECHNIQUES
61
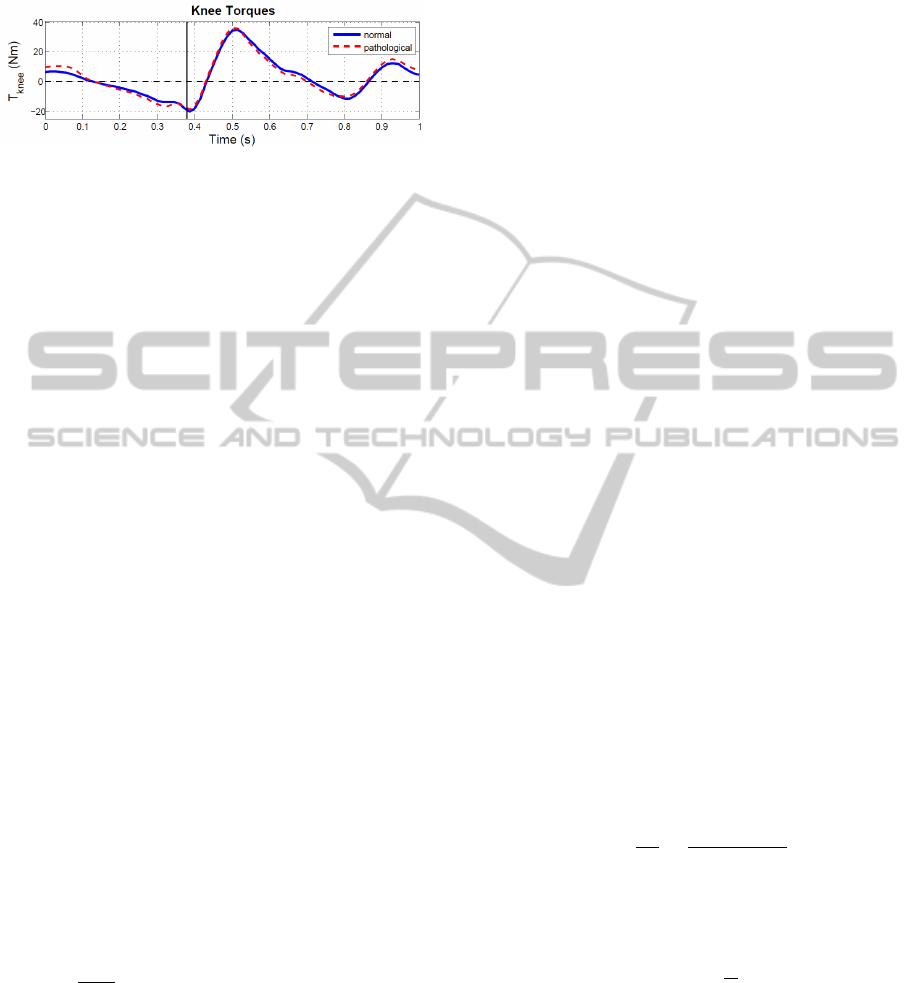
can be observed, only very slight differences can be
found between both torques.
Figure 3: Knee torques during normal gait (solid blue line)
and pathological gait (dashed red line) for the right leg.
Swing phase occurs from 0 to 0.4 in normalized time and
stance phase from 0.4 to 1.
2.3 Optimization Approach: Muscle
and Orthosis Actuation
In order to solve the load sharing problem in biome-
chanics, optimization procedures are used next. There
are several optimization methods (static and dynamic
optimization, large-scale optimization) and optimiza-
tion criteria (minimization of the metabolic cost of
transport, minimization of muscle stresses) in the lit-
erature (Menegaldo et al., 2006; Yamaguchi et al.,
1995). In order to obtain the forces that will be used in
the design of the controller, we use the physiological
static optimization approach (Alonso et al., 2011).
This modified version of the classical static opti-
mization approach considers muscle contraction dy-
namics, ensuring the physiological consistency of the
solution. This approach comprises two steps. In the
first one, the inversion of the contraction dynamics
is solved assuming that muscle activation are max-
ima. The length (l
mt
) and velocity (v
mt
) of each ten-
don unit involved in the process are obtained from
the generalized coordinates of the multi-body model
and the maximum muscle-tendon length (Gerritsen
et al., 1998). Then, the maximum muscle force histo-
ries f
∗
mt
(t) compatible with contraction dynamics are
calculated assuming the muscle activation is maxima
at each instant, i.e. A
m
= [a
1
,. .. , a
N
]
T
= [1,...,1]
T
.
Briefly, for each muscle, the contraction dynamics
differential equation is integrated as:
d f
∗
mt
dt
= g((a = 1) · p, f
∗
mt
,l
mt
,v
mt
). (9)
In the second step, the muscle activations and or-
thosis actuation is calculated by solving the optimiza-
tion problem:
Min J(F
mt
,T
o
) = ω
mt
∑
8
j=1
(− f
ce, j
v
ce, j
)
2
+ ω
0
∑
3
k=1
(T
o,k
˙
θ
k
)
2
s.t. R · (AF
∗
) = T
0 ≤ a
j
≤ 1, j = 1, . .., N = 8
−1 ≤ o
k
≤ 1, k = 1, 2,3
, (10)
where AF
∗
mt
= [a
1
· p
1
· f
∗
mt,1
,. .. , a
8
· p
8
· f
∗
mt,8
,o
1
·
T
∗
o,1
,. .. , o
3
· T
∗
o,3
].
With this approach, muscle forces and orthosis ac-
tuation are calculated for a gait cycle in order to op-
timize the cost function and obtain the parameters of
the PI controller proposed. The 2D walking kinematic
benchmark data from Winter (Winter, 1991) was used
to perform an inverse dynamic analysis. This move-
ment corresponds to a healthy female subject with
57.75 kg of weight with normal gait. Once joint
torques have been calculated, the optimization prob-
lem is solved by using MATLAB routine fmincon im-
plemented in the optimization toolbox that uses a Se-
quential Quadratic Programming (SQP) method. The
simulated muscle-orthosis actuation was performed
for an AIS C subject: motor function partially pre-
served below the neurological level and more than
half of the key muscles below the neurological level
have a muscle grade less than 3. To simulate this
kind of injury, we have defined the following vector
of weakness factor:
p = [1,0.2,1,0.2,0.2,0.2, 0.2, 0.2, ]
T
.
The orthosis actuation prevents stance phase knee
flexion due to quadriceps and assists swing-phase
flexion depending on the ability of each patient, as
shown in the simulation results for the knee in Fig.
4.
3 CONTROLLER DESIGN
In order to control the orthosis, a mathematical model
of the motor is needed. In particular, the following
second order transfer function is used (see (Hossein-
Nia et al., 2011)):
P(s) =
θ
o
V
in
=
3.58
s(0.01s + 1)
. (11)
To control the orthosis, a classic PI controller is
considered as:
C(s) = k
p
+
k
i
s
. (12)
The aim is to tune the parameters k
p
and k
i
in order
to optimize the following cost function,
J =
Z
β(− f
mt
v
mt
)
2
+ (1 − β)e
2
, (13)
with e = θ
k
re f
− θ
k
. This cost function consists of two
parts. The first one corresponds to the muscle power
BIODEVICES 2012 - International Conference on Biomedical Electronics and Devices
62
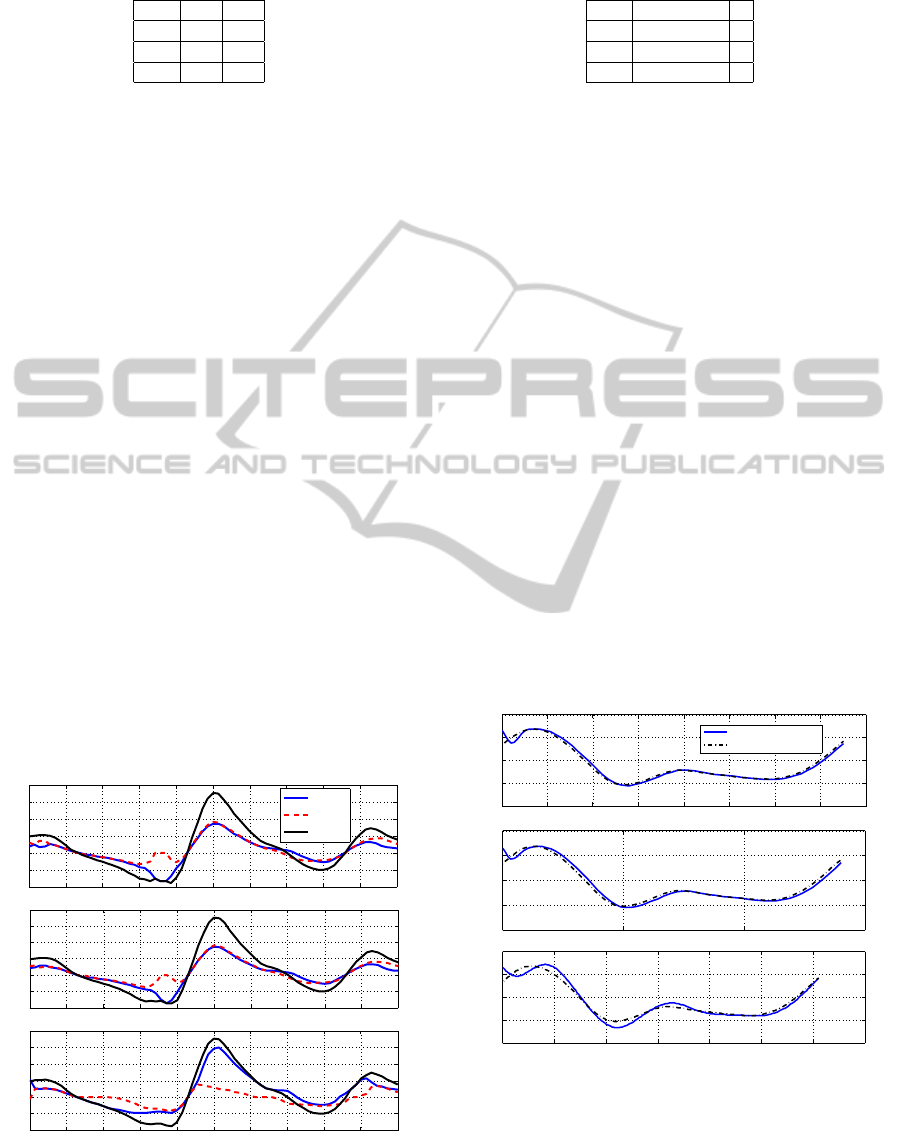
Table 1: The optimized controller parameters.
β k
p
k
i
0.1 40 45
0.5 15 20
0.9 1 6
where f
mt
is the muscular forces obtained by opti-
mization and v
mt
the muscular velocities. The sec-
ond part refers to the error between the knee angle
θ
k
and the reference knee angle θ
k
re f
, respectively.
Two weights 0 < β < 1 and (1 − β) can be chosen
regarding to the muscle power of the patients. The
idea is to design an optimal controller based on the
patients muscle power and the tracking of a reference
signal, where, for the patients with less muscular ca-
pacity, β will be chosen bigger in order to minimize
power and perform the movement and, for patients
with more capacity, the value of β will be minor, so
the cost function prioritizes the minimization of the
tracking error and the movement is going to be made
in less time. Therefore, this controller will consider a
trade off between accuracy of knee movement (con-
cerning healthy human walking) and muscle power
of each patient, taking into account that patients with
less capability need more time to perform the same
movement.
In order to show the performance of the proposed
method, the controller will be designed regarding to
the following three weight options:
• β = 0.1 for the patients with low disability,
• β = 0.5 for the patients with fair disability,
• β = 0.9 for the patients with high disability.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
−20
−10
0
10
20
30
40
T
knee
(Nm)
(β=0.1)
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
−20
−10
0
10
20
30
40
T
knee
(Nm)
Gate cycle
(β=0.9)
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
−20
−10
0
10
20
30
40
T
knee
(Nm)
(β=0.5)
T
orthosis
T
muscle
T
total
Figure 4: Comparsion of orthosis and muscle torque ac-
cording to the patients ability.
Table 2: Final time.
β Final time
0.1 0.75
0.5 1.4
0.9 6.1
Fig. 4 shows the orthosis torque, muscle torque
and total torque corresponding to each controlled sys-
tem (the controller parameters ara given in Table 2).
As can be seen, prioritizing the muscular power with
a big value of β, we consider that patients have a ma-
jor disability and the assistance torque provided by
the orthosis should be higher to compensate the de-
ficiency. On the other hand, prioritizing the tracking
error with a low value of β means that patients have
more ability to perform the movement, so the torque
provided is lower and the movement is achieved in
less time with more accuracy. The final times corre-
sponding to each case are calculated based on mini-
mizing the following mean of integral squared errors
(MISE):
MISE = E
θ
k
− θ
k
re f
2
2
= E
Z
t
f
0
θ
k
(t)− θ
k
re f
(t)
2
dt,
(14)
where t
f
denotes the final time in a gate cycle and
E denotes the expected value with respect to that sam-
ple. Minimizing MISEfor each controller designed,
the final time is obtained based on an optimization
program to satisfy MISE < 0.01):
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
−0.5
0
0.5
1
1.5
θ
k
(rad)
β=0.1
0 0.5 1 1.5
−0.5
0
0.5
1
1.5
θ
k
(rad)
β=0.5
0 1 2 3 4 5 6 7
−0.5
0
0.5
1
1.5
Time (s)
θ
k
(rad)
β=0.9
Knee angle
Reference knee angle
Figure 5: Effect of disability in final time.
Fig. 5 shows the effect of the disability of the pa-
tients in final times. As can be observed, patients with
higher β (considered with disability) need more time
to perform the complete gait cycle than patients with
CONTROLLER DESIGN FOR A STANCE-CONTROL KNEE-ANKLE-FOOT ORTHOSIS BASED ON
OPTIMIZATION TECHNIQUES
63

low value of β, corresponding to low disability. In the
same way, high disability correspond to higher track-
ing error, and lower disability correspond to a better
accuracy in the performance of the movement com-
pared with the healthy subject.
4 CONCLUSIONS
In this paper, in order to control an orthosis, an op-
timal approach is proposed to design a PI controller
according to disability of the patients. This disabil-
ity is simulated by means of physiological static opti-
mization approach where the muscular forces of SCI
are obtained in a process that combines the actuation
of the muscles and the external actuation provided by
the orthosis. Those forces are used to design a proper
controller for the external actuation. Considering pa-
tients with a high disability, the controller is tuned to
perform the movement so as to allow the patient to
achieve the movement but in a longer cycle compared
with patients with less disability, where the controller
is tuned giving priority to the accuracy of the move-
ment. Patients with less power in his muscle –high
disability–, need more time in a gate cycle to walk,
whereas patients with low disability need less time.
This idea is shown through some three types of dis-
ability, i.e. high disability, fair disability and low dis-
ability. The simulation results show the efficiency of
the proposed method.
ACKNOWLEDGEMENTS
This work was supported by the Spanish Ministry of
Science and Innovation under the project DPI2009-
13438-C03. The support is gratefully acknowledged.
REFERENCES
Ackermann, M. (2007). Dynamics and energetics of
walking with prostheses. PhD thesis, University of
Stuttgart.
Ackermann, M. and Schiehlen, W. (2006). Dynamic anal-
ysis of human gait disorder and metabolical cost esti-
mation. Archive of Applied Mechanics, 75:569–594.
Alonso, J., Romero, F., P
`
amies-Vil
`
a, R., Lugr
´
ıs, U., and
Font-Llagunes, J. (2011). A simple approach to esti-
mate muscle forces and orthosis actuation in powered
assisted walking of spinal cord-injured subjects. Proc.
EUROMECH Coll. 511 Biomechanics of Human Mo-
tion 2011, Ponta Delgada, Azores, Portugal.
Amankwah, K., Triolo, R., and Kirsch, R. (2004). Ef-
fects of spinal cord injury on lower-limb passive joint
moments revealed through a nonlinear viscoelastic
model. Journal of Rehabilitation Research & Devel-
opment, 41:15–32.
Dollar, A. and Herr, H. (2008). Lower extremity exoskele-
tons and active orthoses: challenges and state-of-the-
art. IEEE T Robotics, 24:1–15.
Edrich, T., Riener, R., and Quintern, J. (2000). Analysis of
passive elastic joint moments in paraplegics. IEEE
Transactions on Biomedical Engineering, 47:1058–
1065.
Filippi, P. (1942). Device for the automatic control of the
articulation of the knee applicable to a prosthesis of
the thigh.
Font-Llagunes, J., P
`
amies-Vil
`
a, R., Alonso, J., and Ur-
bano Lugr
´
ıs, U. (2011). Simulation and design of an
active orthosis for an incomplete spinal cord injured
subject. Procedia IUTAM, 2:68–81.
Gerritsen, K., van den Bogert, A., Hulliger, M., and Zer-
nicke, R. (1998). Intrinsicmuscle properties facilitate
locomotor control: a computer simulation study. Mo-
tor Control, 2.
HosseinNia, S., Romero, F., Vinagre, B., Alonso, F., Te-
jado, I., and Font-Llagunes, J. (2011). Hybrid model-
ing and fractional control of a sckafo orthosis for gait
assistance. In ASME 2011 International Design En-
gineering Technical Conferences and Computers and
Information in Engineering Conference.
Kao, P., Lewis, C., and Ferris, D. (2010). Invariant ankle
moment patterns when walking with and without a
robotic ankle exoskeleton. Journal of Biomechanics,
43:203–209.
Lebiedowska, M. and Fisk, J. (1999). Passive dynamics of
the knee joint in healthy children and children affected
by spastic paresis. Clinical Biomechanics, 14(9):653–
660.
Menegaldo, L., Fleury, A., and Weber, H. (2006). dd. Jour-
nal of Biomechanics, 39:1787–1795.
Silva, P. C., Silva, M. T., and Martins, J. M. (2010). Eval-
uation of the contact forces developed in the lower
limb/orthosis interface for comfort design. Multibody
System Dynamics, 24:367–388.
Thomas, C. and Grumbles, R. (2005). Muscle atrophy after
human spinal cord injury. Biocybernetics & Biomedi-
cal Engineering, 25:39–46.
Vukobratovic, M., Ciric, V., and Hristic, D. (1972). Contri-
bution to the study of active exo-skeletons. Proceed-
ings of the 5th IFAC Congress, Paris, France,.
Winter, D. (1991). Biomechanics and motor control of hu-
man gait: normal, elderly and pathological. Univer-
sity of Waterloo Press, 2nd edition.
Yamaguchi, G., Moran, D., and Si, J. (1995). A compu-
tationally efficient method for solving the redundant
problem in biomechanics. Journal of Biomechanics,
28:999–1005.
Zajac, F. (1989). Muscle and tendon: Properties, models,
scaling and applications to biomechanics and motor
control. Critical Reviews in Biomedical Engineering,
17:359–411.
BIODEVICES 2012 - International Conference on Biomedical Electronics and Devices
64
