GRADIENT ARTEFACT CORRECTION IN THE EEG

SIGNAL RECORDED WITHIN THE fMRI SCANNER

José L. Ferreira

, Pierre J. M. Cluitmans

and Ronald M. Aarts

1,2

Department of Electrical Engineering, Eindhoven University of Technology, Eindhoven, The Netherlands

Philips Research Laboratories Eindhoven, Eindhoven, The Netherlands

Keywords: Combined EEG-fMRI, Imaging artefact correction, Average artefact subtraction, Artefact template

variability modelling.

Abstract: In recent years, combined EEG-fMRI has become a powerful brain imaging technique which is largely

employed in clinical and neuroscience research. Parallel to the achievements reached in this area, a number

of challenges remain to be overcome in order to consolidate such technique as an independent and effective

method for brain imaging. In particular, the occurrence of gradient artefacts in the EEG signal due to the

magnetic field of the fMRI magnetic scanner. This paper presents a proposal for modelling the variability of

the gradient artefact template which makes use of the standard deviation and the slope differentiator

between consecutive samples of the signals. Combination of such a model with the average artefact

subtraction method achieves a reasonable elimination of the gradient artefact from EEG recordings.

1 INTRODUCTION

Combined EEG-fMRI (acquisition of

electroencephalogram during functional magnetic

resonance imaging) is a technique for multimodal

brain activity mapping that has got a broad usage for

research and clinical purposes (Villringer et al.,

2010). Ritter and Villringer (2006) reinforce that co-

registered EEG-fMRI has attracted the interest of

several researchers and clinicians last years and it

has revealed itself a promising and additional

monitoring tool of the human brain activity.

Gonçalves et al. (2007) mention that although

such a brain imaging technique was first applied in

the field of epilepsy, nowadays it has been extended

to other types of neuroscience studies and

applications. Villringer et al. (2010) mention that

only simultaneous EEG-fMRI offers the opportunity

to relate both brain imaging modalities to actual

brain events, a characteristic which is relevant for

solving numerous research questions in basic and

cognitive neuroscience.

Parallel to the breakthroughs achieved by using

simultaneous combination of EEG-fMRI as an

independent brain imaging technique, some

problems related to its use remain to be solved in

order to consolidate and to enable broadening its

applications range. That is the case of the occurrence

of artefacts in the EEG signal caused by the

variation of the magnetic fields of the fMRI scanner,

the so-called “gradient” or “imaging acquisition”

artefact (Mulert and Hegerl, 2009).

2 OBJECTIVES

Gradient artefacts completely obscure the EEG, as

illustrated in figure 1. According to Ritter et al.

(2010), this type of artefact occurs in the EEG signal

due to the voltage induced by the application of

rapidly varying magnetic field gradients for spatial

encoding of the MR signal and radiofrequency

pulses (RF) for spin excitation in the circuit formed

by the electrodes, leads, patient and amplifier.

The waveform of the gradient artefact caused by

one RF pulse is approximately the differential

waveform of the corresponding RF pulse. Imaging

acquisition artefacts have amplitudes that can be

several orders of magnitude higher than the neuronal

EEG signal. Artefact amplitudes associated to the

gradient switching (10

to 10

μV) are generally

much larger than those arising from RF pulses (up to

μV) (Ritter et al., 2010).

110

Ferreira J., Cluitmans P. and Aarts R..

GRADIENT ARTEFACT CORRECTION IN THE EEG SIGNAL RECORDED WITHIN THE fMRI SCANNER.

DOI: 10.5220/0003788001100117

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2012), pages 110-117

ISBN: 978-989-8425-89-8

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Imaging artefact in ongoing EEG data. Adapted

from Mantini et al. (2007).

As discussed by Ritter et al. (2010), the

frequency range of the gradient artefact exceeds that

of standard clinical EEG, nevertheless the EEG

recording is dominated by harmonics of the

repetitive slice convolved with harmonics in the

range of frequency of the volume repetitive

frequency. The frequency of these harmonics

overlaps the range frequency of the EEG signal.

Moreover, also as mentioned by Ritter et al., such

artefacts have a strong deterministic component

because the preprogrammed nature of RF and

gradient switching.

In literature, some techniques are suggested in

order to attempt minimizing the effects of gradient

artefacts in the EEG signal. For example, it is

possible to reduce their magnitude at the source by

laying out, immobilising and twisting the EEG leads,

using a bipolar electrode configuration and using a

head vacuum cushion. Further, depending on the

application, a periodic interleaved approach,

whereby the MR signal acquisition is suspended at

regular intervals, could be used as well (Ritter et al.,

2010).

Gonçalves et al. (2007) mention that concerning

continuous MR acquisition, dedicated software

solutions have to be developed in order to correct

gradient artefacts in the electroencephalogram.

Some post-processing signal methods for correction

of gradient artefacts in the EEG signal are based

upon time or frequency domain analysis which make

use of different mathematical and computational

digital signal processing approaches like spectrum

analysis, principal component analysis, independent

component analysis and average artefact subtraction

(Gonçalves et al., 2007).

According to Allen et al. (2000), the average

artefact subtraction methodology consists of the

calculation of an average imaging artefact waveform

or template over a fixed number of samples, and it is

then subtracted from the EEG signal for each

sample.

Performing average artefact subtraction alone

does not result to satisfactory quality of corrected

signal, demanding the need for further residuals

correction (Allen et al., 2000; Gonçalves et al.,

2007). These authors also propose the use of

adaptive noise cancelling for attenuating the

remaining residuals from the subtraction by using

low-pass filters, smoothing and downsampling.

However, according to Van de Velde et al. (1998),

the use of filtering could result in removing original

component frequencies of the EEG signal.

The objectives of the current paper are to present

an alternative approach for cleaning up such

residuals by employing a specific model for

evaluating and quantifying the variability of the

imaging artefact. The proposed methodology is

based upon information about the variance of the

averaged template artefact as well as on the slope

differentiator of the EEG signals under analysis.

3 MATERIALS AND METHODS

3.1 Features of the Data under

Analysis

Simultaneous EEG and fMRI data were collected for

a research focused on epilepsy and post-traumatic

stress disorder (PTSD), jointly developed by the

department of Psychiatry of Universiteit Medisch

Centrum Utrecht, the Research Centre Military

Mental Health Care in the Dutch Central Military

Hospital in Utrecht and the Department of Research

and Development of the Epilepsy Center of

Kempenhaeghe in Heeze (The Netherlands).

Data were recorded from patients characterized

as military veterans with PTSD which were in

mission abroad through the outpatient clinic of the

Military Mental Health Care. All participants were

male and aged between 18 and 60 years.

3.2 Protocol for EEG-fMRI Data

Collection

Functional magnetic resonance imaging scanning

was carried out using a 3 T Scanner (Philips,

Eindhoven, The Netherlands) at Kempenhaeghe

Epilepsy Center. An MRI-compatible 64 channel

polysomnograph was used to collect one ECG

channel, two EOG channels, one EMG and 60 EEG

GRADIENT ARTEFACT CORRECTION IN THE EEG SIGNAL RECORDED WITHIN THE fMRI SCANNER

111

channels. In the current work, the ECG signal was

used for synchronization purposes. EEG electrodes

positioning was in accordance with the international

10-20 system electrodes placement.

EEG-fMRI data were collected during 45

minutes, before the period that the patient should

sleep. After application of the EEG cap, the subjects

were scanned using a functional echo-planar

imaging sequence with 33 transversal slices

(thickness 3 mm, TE 30 ms, TR 2500 ms).

The used electroencephalogram device for

collecting the EEG signals possesses an appropriate

built-in notch filter. The sampling rate for signal

acquiring was 2048 Hz.

3.3 General Average Artefact

Subtraction Overview

The basic idea of the average subtraction approach

consists of estimating an average template of the

gradient artefact along an observed range of the

EEG signal, and then subtracting this template from

the electroencephalogram at those regions where the

artefact occurs (Allen et al., 2000). The average

artefact subtraction can be described by the

following expression:

iii,rawi,corct

EEGGEE

−

−= Γ



(1)

where i runs over the number of samples within the

entire EEG data set; i-i

is the time sample along the

selected EEG segments considered for average;

EÊG

corct

and EEG

raw

are respectively the corrected

and the uncorrected (raw) EEG signals; and Γ is the

template to be subtracted.

According to the methodology proposed by

Allen et al. (2000) to calculate such a template, the

EEG

raw

is divided in segments of fixed length (S

number of samples). The resulting averaging from

samples situated at the same segment position i-i

corresponds to the template epoch

ii−

Γ .

Allen et al. (2000) and Gonçalves et al. (2007)

also consider the need for interpolation and

extrapolation along the obtained fixed segment

length. According to the approach for average

gradient subtraction proposed by Gonçalves et al.

(2007), interpolation is necessary since in general

the clocks of the EEG and fMRI are uncalibrated

and, in consequence, misaligned. Thus, a small time

shift should be applied in order to compensate the

misalignment and to eliminate the variation of the

number of epochs among the slices segments.

Gonçalves et al. (2007) still take into account

estimation of some parameters which must be

computed before carrying out the artefact

subtraction like the slice time (ST) and the dead time

(DT) which are determined by minimizing a cost

function that is related to the ratio between EÊG

corct

and EEG

raw

3.4 Overview of the Average Artefact

Subtraction Methodology

Employed in this Work

In order to perform the estimation of the corrected

EEG, EÊG

corct

, the model described in (1) was

employed. In this sense, estimation of Γ was done

by dividing the chosen range of the observed

EEG

raw

in segments with fixed length, as proposed

by Allen et al. (2000) and Gonçalves et al. (2007).

However, due to some specific features observed in

the data analysed in the current work, a different

approach to estimate the length of those segments

was used.

Observation of the raw EEG data recorded

during the MR scanning revealed that the slice

length could be estimated by evaluation of the

distance between typical peaks noticed in the raw

EEG or ECG recordings that can be attributed to the

magnetic fields switching within the MR scanner

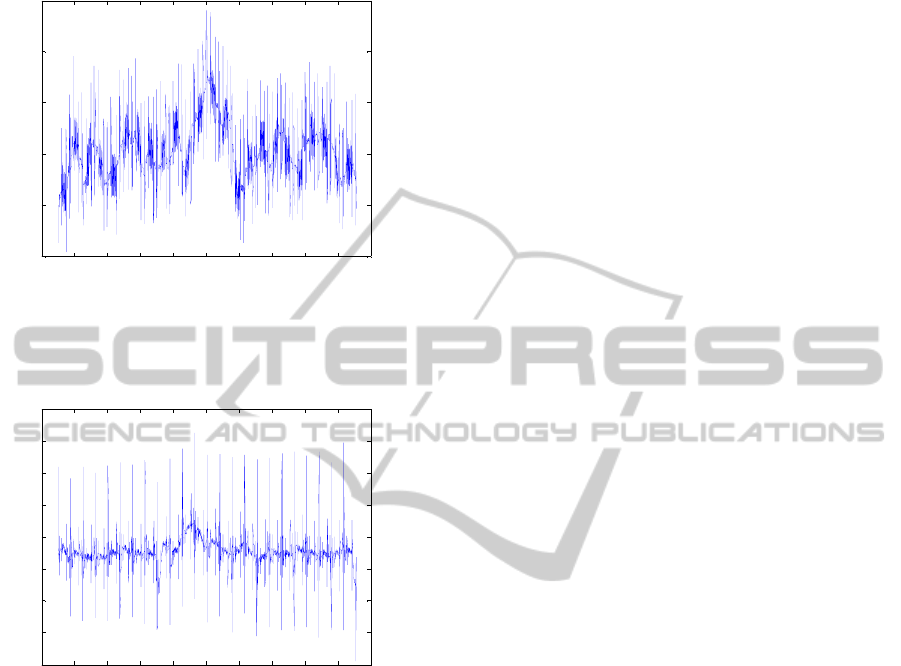
(Ritter et al., 2010). Figures 2 and 3 show the

occurrence of those peaks in 2 s-segments of the raw

EEG (electrode position F8) and raw ECG around

the time instant 429.4 s.

It is important to highlight that estimation of

such a distance from the EEG data recorded within

the scanner was necessary since: i) the

electromagnetic properties of different sources of

the system constituted by the electroencephalograph,

the fMRI scanner and patient have influence on the

artefact generation and morphology; ii) that is the

existing condition for the available data under

analysis. Thereby, it could not be evaluated just by

placing one electrode directly in the fMRI scanner.

Performing measurement of the distance

between peaks by using such a procedure allowed to

estimate the value of ST around (155 ± 1) epochs

that correspond to a time interval of approximately

(0.07568 ± 0.00050) s considering the data under

analysis in this work.

Thus, as a first approach, the used segment

length was the slice length itself, and EEG was

divided in segments of 155 epochs, according to the

measured distance between the peaks corresponding

to the beginning of each MR slice. In the case of the

segments that contained more or less than 155

epochs, extrapolation or interpolation were done in

order to fix the length of the segments and therefore

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

112

to compensate the misalignment between the EEG

and fMRI clocks (Gonçalves et al., 2007).

428.4 428.6 428.8 429 429.2 429.4 429.6 429.8 430 430.2 430.4

2.55

2.555

2.56

2.565

2.57

2.575

x 10

Raw EEG signal - F8

Signal (

Time (s)

Figure 2: 2 s-segment around the time instant 429.4 s of

the raw EEG signal (electrode position F8), showing the

peaks caused by MR switching.

428.4 428.6 428.8 429 429.2 429.4 429.6 429.8 430 430.2 430.4

2.2

2.3

2.4

2.5

2.6

2.7

2.8

2.9

x 10

Raw ECG signal

Signal (

Time (s)

Figure 3: 2 s-segment around the time instant 429.4 s for

the raw ECG signal, showing the peaks caused by MR

switching.

The algorithm used for performing the average

subtraction was adapted from Bishop (2006) and

Press et al. (1992), and is based upon the idea that

the mean of a random variable corresponds to the

point where the random variable has the minimum

variance. By this approach, epochs from the

different segments in which the raw EEG was

divided and have a corresponding position within the

slice,

j,i,raw

EEG

, can be related to an initial choice

for the template average epoch at the same slice

position,

i-i

μ (=

ii−

Γ ), by the following cost

function:

∑

−=

j,iraw,i-i

i-is

EEG

)μ()(μΨ

i-i

(2)

where J is the number of slices considered for

averaging. The rationale for using this formula is

that in addition to calculate the averaged gradient

artefact template, minimization of (2) provides to

estimate jointly the variance (standard deviation)

associated to each epoch, parameter which is used

during modelling and correction of the artefact

variability as described in the next section. (2) can

be rewritten into the following matrix format:

⋅=)(μΨ

i-is

i-i

(3)

where K is a vector with Jx1 components

i-ij,iraw,j

EEGK μ−=

. Therefore, the value of

i-i

is the variance associated to the template

epoch i-i

. Finally, the values of EÊG

corct

(and Γ)

can be calculated from:

⋅

(4)

The square root of the diagonal elements of Z

corresponds to the values of EÊG

corct,i

3.5 Modelling of Imaging Artefact

Template Variability

For elimination of the remaining residuals in the

EÊG

corct

, a specific model is proposed for

attempting to quantify the artefact variability. The

use of this alternative approach was preferred since,

according to Van de Velde et al. (1998), the use of

filtering, as is done for conventional residuals

elimination, could also remove some original

frequencies of the EEG signal. Furthermore, the

remaining artefact residuals can be attributed to the

template variability.

Klados et al. (2009) suggest the use of an

adaptive method whereby it is possible to

approximate the EÊG

corct

to the true EEG.

According to that methodology, the template

variability is evaluated by multiplying each artefact

template sample by an estimated factor â

, and then

subtraction is processed as follows:

iiii,rawi,corct

aEEGGEE

−

−= Γ



(5)

The expression above is an adaptive extension of

(1) whose limit referred to the filter parameter â

allows refining the value of EÊG

corct

i,corcti,corct

aâ

EEGGEE

→



lim

(6)

Therefore as far as the parameter â is approached

to the optimal value of the adaptive filter a, the value

of EÊG

corct

tends to the true EEG.

GRADIENT ARTEFACT CORRECTION IN THE EEG SIGNAL RECORDED WITHIN THE fMRI SCANNER

113

In the current work, this method was further

modified in such a way that â is changed to a new

non-filter parameter â’ and equations (5) and (6)

become:

iii,corcti,corct

R'aGEEEEG



−=

(7)

where the product of the corresponding elements of

the vectors â’ and R acts as an initial estimation of

the remaining residual in the EEG. Hence, (7) allows

to calculate a refinement for the value of the

corrected EEG by subtracting an estimation of the

remaining residual from the corresponding unrefined

value obtained for EÊG

corct

As the parameters â’ and R should represent the

variability of the gradient artefact, their estimation

took into account specific properties of the raw,

corrected signal and true EEG that are supposed to

reflect that variability. The standard deviation

associated to the averaged imaging artefact and the

signal slope differentiator were chosen as the

properties of the signals that represents the

variability, the former was associated to â’ and the

latter to R.

Concerning the standard deviation associated to

the averaged artefact, it is a natural choice since it is

a measurement of the variability of a random

variable around the mean (Papoulis and Pillai,

2002). According to the GUM (2008) the standard

deviation (or the variance) also could be seen as a

component of the uncertainty measurement

associated with the estimated average, and therefore

could be used for quantifying and correcting the lack

of information about the variability of the random

variable.

The choice of the slope differentiator is in

accordance with Van de Velde et al. (1998) that

describe such a signal parameter associated to the

large signal magnitudes as being particularly useful

for detection of the high-frequency properties of the

muscle artefact. At the same way, by observing the

EEG signals under analysis, it is noticed that high-

frequency as well as large signal magnitudes can be

attributed to the gradient artefact. Thereby, in our

work, the slope variation is also used to identify the

imaging acquisition artefact. Moreover, a new

approach is proposed to quantify the variability

making use of the signal slope as well, as described

below.

In our approach, estimation of the parameter R is

based upon the simple differentiation of EEG

raw

diff (EEG

raw

), EÊG

corct

, diff (EÊG

corct

), and the

artefact free EEG. An artefact free EEG interval

could be obtained from the available data, from

approximately the first 5 s of the recordings of each

EEG channel, allowing estimating the corresponding

values for the slope differentiator.

By analysing the artefact free interval, it could

be observed that the maximum value of the slope

differentiator of the true EEG is estimated around

15 μV/sample. The values observed for the same

parameter, considering EEG

raw

and EÊG

corct

, are

usually much higher when compared to the true

EEG in such a way that it allows identification of

epochs as being artefact free or not, which is in

accordance with the methodology proposed by Van

de Velde et al. (1998). The values of the elements of

R were quantified by taking into account the

normalized values of diff (EÊG

corct

), whose

maximum value was considered as being equal to 1,

as follows:

)(max

)(

corct

GEE



diff

GEEGEE

i,corct1i,corct

i,norm

−

(8)

Thus, R

norm,i

corresponds to the normalized value

of diff (EÊG

corct

As mentioned above, the elements of vector â’

(i.e., â

’) were related to the value of standard

deviation

−



of the gradient average artefact, as

indicated in (9) and 10:

iii

s'a

−



;

(9)

−



is equal to the root square of the template

variance:

-iiii

s Ψ=

−



(10)

Finally, considering (8), (9) and (10), expression

(7) can be rewritten as:

i,normiii,corcti,corct

RsGEEEEG

−

−=



(11)

Therefore, the limit described in equation (6) is

carried out by performing the subtraction indicated

in (11) iteratively, until a predetermined threshold

value is reached. In this work, the threshold was set

as being the value of diff (EEG

corct

) coincident with

the mean plus the standard deviation calculated for

the slope differentiator of the true EEG (estimated

around 1.5 μV/sample for the available data).

It is worthwhile to consider that in our approach

the values of the parameter R

norm,i

act as weights

varying from 0 to 1 which indicate what percentage

of the standard deviation should be applied for

refinement of EÊG

corct

. In other words, the value of

norm,i

acts as an indicator of the presence of the

gradient artefact in

EÊG

corct

(Van de Velde et al.,

1998) and at the same time indicates the amount of

correctness based on that should be applied on

EÊG

corct,i

−



−



BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

114

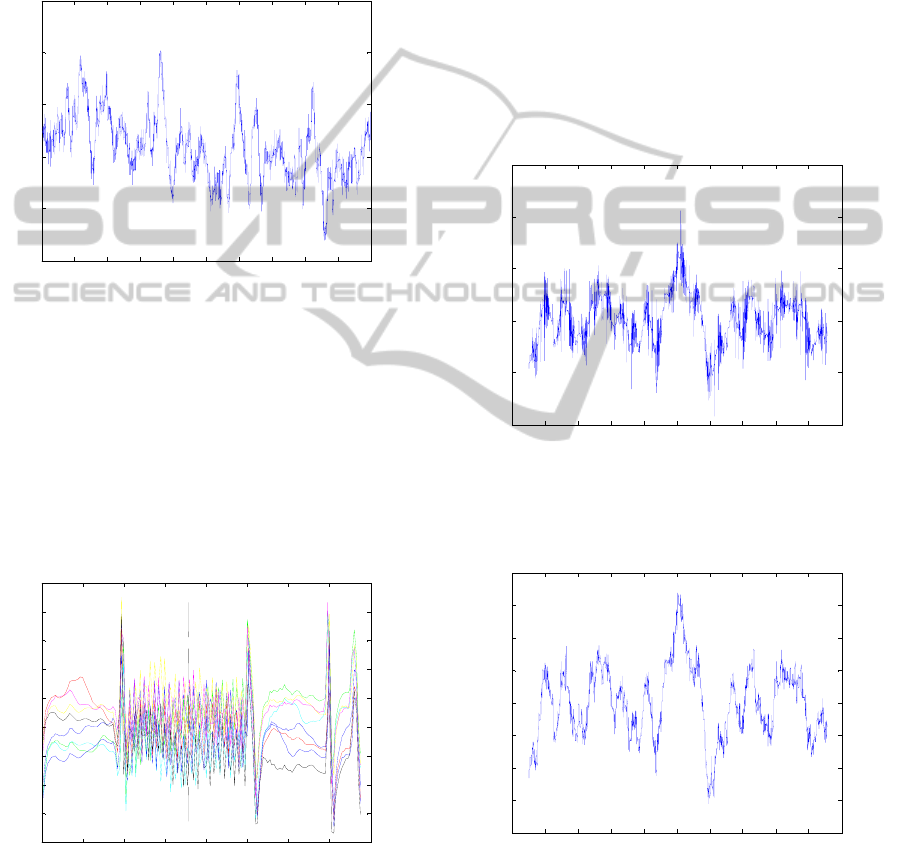
4 RESULTS

In figure 4, the artefact free 5 s-period of the raw

EEG corresponding to the EEG at channel F8 is

depicted. It is noticed that there is a DC offset in the

signal around 2.55 x 10

μV. A similar DC

component is also observed for the other electrode

EEG positions and ECG recording.

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

2.54

2.545

2.55

2.555

2.56

2.565

x 10

Raw EEG signal - F8

Signal (

Time (s)

Figure 4: Artefact free period of raw EEG signal

recording, corresponding to electrode position F8. A DC

component around 2.55 x 10

μV can be observed.

In order to estimate the artefact template Γ, a set

of eight subsequent segments (J = 8 slices) were

considered from the raw EEG signal. Figure 5 shows

one set of slices picked up from the raw EEG signal

already containing interpolated or extrapolated

epochs depending on the need, and used during the

calculations.

0 20 40 60 80 100 120 140 160

2.552

2.554

2.556

2.558

2.56

2.562

2.564

2.566

2.568

2.57

x 10

Epoch

Signal (

Set of eight slices considered for artefact template estimation

i-i

Figure 5: Set of eight (J = 8) subsequent EEG segments

slice-length (155 epochs) around the time instant of 430 s

considered for averaging. The average template Γ is

calculated considering corresponding epochs of each

segment (Allen et al., 2000).

Figure 6 shows the results of the average artefact

subtraction described by application of equations

(2), (3) and (4) on the raw EEG signal showed in

figure 2. Nevertheless the observed DC component

has been removed, in comparison to the artefact free

EEG signal of figure 4, a considerable amount of

remaining residual peaks uniformly distributed along

the signal resulting from the gradient artefact are

still observed in figure 6.

Hence, in order to obtain a better correction for

EÊG

corct

, equations (8) to (11) are then applied to

the signal of figure 6, resulting to the signal depicted

in figure 7. From this figure, it could be seen that the

noticed residuals in figure 6 were strongly cleaned

up.

428.4 428.6 428.8 429 429.2 429.4 429.6 429.8 430 430.2 430.4

-100

-50

100

150

Corrected EEG with remaining residuals - F8

Signal (

Time (s)

Figure 6: Signal resulting (EÊG

corct

) from application of

equations (2), (3) and (4) on the signal of figure 2.

428.4 428.6 428.8 429 429.2 429.4 429.6 429.8 430 430.2 430.4

-80

-60

-40

-20

Corrected EEG cleaned from residuals - F8

Signal (

Time (s)

Figure 7: Signal resulting (EEG

corct

) from application of

equations (8) to (11) on the signal of figure 6.

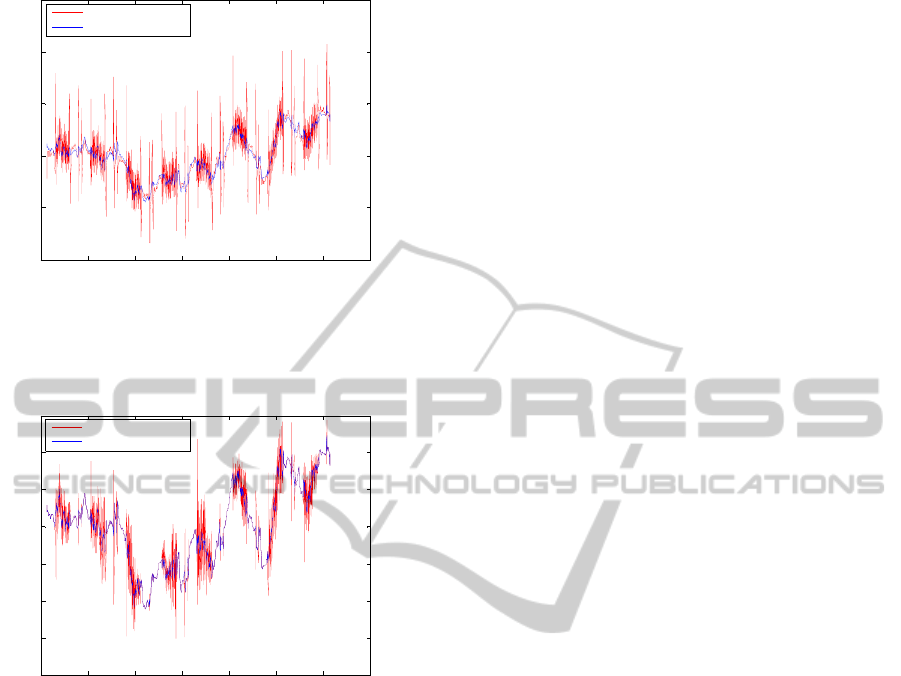
Finally, figures 8 and 9 depict zooming in (0.7 s-

segment length) around the time instant 430 s,

showing superposition of the signals raw EEG and

EEG

corct

, and the signals EÊG

corct

and EEG

corct

GRADIENT ARTEFACT CORRECTION IN THE EEG SIGNAL RECORDED WITHIN THE fMRI SCANNER

115

430 430.1 430.2 430.3 430.4 430.5 430.6 430.7

-100

-50

100

150

Raw EEG and EEG cleaned from residuals - F8

Signal (

Time

(

)

Raw EEG

Cleaned from residuals

Figure 8: 0.7 s-segment around the time instant 430 s of

the signal EEG

corct

(cleaned from residuals) superimposed

to the raw EEG (without DC offset).

430 430.1 430.2 430.3 430.4 430.5 430.6 430.7

-80

-60

-40

-20

EEG average subtracted and EEG cleaned from residuals - F8

Signal (

Time (s)

Average subtracted

Cleaned from residuals

Figure 9: 0.7 s-segment around the time instant 430 s of

the signal EEG

corct

(cleaned from residuals) superimposed

to EÊG

corct

(average subtracted).

5 DISCUSSION

As can be regarded in figure 8 and 9, combination of

the methods average artefact subtraction with the

approach here proposed for cleaning up the resulting

residuals from that subtraction have achieved a

strong elimination of the gradient artefact from the

raw EEG signal.

As regarded in figure 6, just the average artefact

subtraction approach described in equations (2), (3)

and (4) does not result to satisfactory elimination of

the artefact from the EEG signal since a

considerable amount of residuals remains in the

resulting corrected signal (figure 6). Such residuals

can be attributed to the variability of the imaging

artefact and this information is not taken into

account when only the average is used in the

correction. Nevertheless the waveform of the

gradient artefact possesses a strong deterministic

(Ritter et al., 2010) and reproducible component, as

could be noticed in figure 5, the variability

associated with the artefact provokes the presence of

residuals in the corrected EEG and, therefore, the

need for further correction.

Hence, in our approach for removing the artefact

residuals, it is proposed to use additional

characteristics from the available data which could

contain some information about the template

variability as well as which could enable to quantify

the magnitude of the residuals. The two chosen

signal characteristics were the standard deviation

associated to the averaged (Papoulis and Pillai,

2002; GUM, 2008) template and the signal slope

differentiator (Van de Velde et al., 1998), and

showed themselves fit those requirements since the

use of equations (5) to (11) allows elimination of the

residuals as is depicted in figure 7.

Therefore, combination of the average artefact

subtraction method and the methodology for

quantifying the variability of the template of the

imaging artefact proposed here reveals itself to be an

alternative method for cleaning up the EEG signal

from the gradient artefact, which could produce a

good quality for the resulting corrected signal.

Nevertheless the model described in equations (5) to

(11) constitutes a prototype and requires more

accurate refinement and validation, some advantages

of its application could be mentioned in comparison

to other methods.

Firstly, the employed approach is implemented

only in the time domain. In addition, it does not

requires insertion of markers in the EEG signal since

the value of important events associated to the MR

scanning like ST, DT and TR could be evaluated

directly from data (observed peaks in the raw signals

caused by the imaging artefact). Furthermore, the

entire estimation of the model parameters is based

upon the use of simple statistical parameters of the

signals like mean, standard deviation and mode.

Another observed advantage of the employed

methodology is that, in principle, a low number of

slices could be used during template averaging

without the need for using the slices of the entire

MR volume as well as recordings from other EEG

channels. This consideration could be useful in

future developments concerning real time

applications. Finally, in principle there is no need for

using filtering; this fact will be evaluated in future

steps for method validation.

The use of the synchronized ECG signal was

useful during application of the proposed

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

116

methodology since the events related to the MR

scanning occur simultaneously in the EEG and the

ECG recordings, in such a way that the

electrocardiogram can be used for estimation of

relevant parameters associated to the proposed

correction methodology which also are valid for the

electroencephalogram.

6 CONCLUSIONS

A prototype model for quantifying the gradient

template variability combined with the average

artefact template subtraction methodology was

applied for removing gradient artefact from EEG

signals, and proves to be promising as an alternative

approach for obtaining a good signal correction.

As described in literature (Allen et al., 2000;

Gonçalves et al., 2007), the average artefact

subtraction alone does not result to satisfactory

quality of corrected signal, demanding the need for

further residuals correction. As discussed by Van de

Velde et al. (1998), the use of filtering could result

in removing original component frequencies of the

EEG signal. Therefore, in this work a model for

identification and quantification of the residuals to

be subtracted is proposed, instead the usual

employment of low-pass filtering for cleaning up the

remaining residuals.

In future work, the influence of a higher number

of slices (for instance, the entire number of slices of

the MR volume) must be checked as well as signal

estimation of the time intervals corresponding to the

dead time (DT) have to be carried out using the

presented approach. Also, the proposed model has to

be applied to a larger set of EEG clinical data in

order to evaluate its consistency.

Finally, as an additional recommendation for

future work, it should be analyzed if the proposed

methodology could be extended for correction of

other types of artefact as well as could be

consolidated as an alternative average subtraction

approach for signal correction.

ACKNOWLEDGEMENTS

We are grateful to Saskia van Liempt, M.D., and

Col. Eric Vermetten, M.D., Ph.D. from the

University Medical Center/Central Military

Hospital, Utrecht, for providing the data presented in

this work. This work has been made possible by a

grant from the European Union and Erasmus

Mundus – EBW II Project.

REFERENCES

Allen, P., Josephs, O., Turner, R., 2000. A method for

removing imaging artefact from continuous EEG

recorded during functional MRI. NeuroImage. 12.

Elsevier: 230-239.

Bishop, C., 2006. Pattern recognition and machine

learning. Springer: New York.

Gonçalves, S., Pouwels, P., Kuijer, J., Heethaar, R., de

Munck, J., 2007. Artefact removal in co-registered

EEG/fMRI by selective average subtraction. Clinical

Neurophysiology. 118. Elsevier: 823-838.

GUM, 2008. Evaluation of measurement data – Guide to

the expression of uncertainty in measurement. 1

ed.

JCGM.

Klados, M., Papadelis, C., Bamidis, P., 2009. A new

hybrid method for EOG artefact rejection. 9

International Conference on Information Technology

and Application in Biomedicine, ITAB 2009, Larnaca,

Cyprus, November 5-7, 2009, Proceedings: 4937-

4940.

Mantini, D., Perucci, M., Cugini, S., Romani, G., Del

Gratta, C., 2007. Complete artefact removal for EEG

recorded during continuous fMRI using independent

component analysis. NeuroImage. 34. Elsevier: 598-

607.

Mulert, C., Hegerl, U., 2009. Integration of EEG and

fMRI. In E. Kraft, G. Gulyás, E. Pöppel (eds.), Neural

correlation of thinking. Springer: Verlag, Berlin,

Heidelberg.

Papoulis, A.; Pillai, S., 2002. Probability, random

variables, and stochastic processes. 4

ed. New York:

McGraw-Hill.

Press, W.; Teukolsky, S.; Vetterling, W; Flannery, B.,

1992. Numerical recipes in C: the art of scientific

computing. 2

ed. Cambridge University Press:

Cambridge.

Ritter, P., Becker, R., Freyer, F., Villringer, A., 2010. EEG

quality: the image acquisition artefact. In C. Mulert, L.

Limieux (eds.), EEG-fMRI: Physiological basis,

technique and applications. Springer: Verlag, Berlin,

Heidelberg.

Ritter, P., Villringer, A., 2006. Simultaneous EEG-fMRI.

Neuroscience and Biobehavioral Reviews. 30.

Elsevier: 823-838.

Van de Velde, R., Van Erp, G., Cluitmans, P., 1998.

Detection of muscle artefact removal in the normal

human awake EEG. Electroencephalography and

Clinical Neurophysiology. 107. Elsevier: 149-158.

Villringer, A., Mulert, C., Lemieux, L., 2010. Principles of

multimodal functional imaging and data integration. In

C. Mulert, L. Limieux (eds.), EEG-fMRI:

Physiological basis, technique and applications.

Springer: Verlag, Berlin, Heidelberg.

GRADIENT ARTEFACT CORRECTION IN THE EEG SIGNAL RECORDED WITHIN THE fMRI SCANNER

117