MOBILE SPEED AND POSITION SENSOR FOR HOME HEALTH

MONITORING BASED ON ACCELEROMETER SIGNALS

Tamás Dabóczi and Arnold Kalvach

Department of Measurement and Information Systems, Budapest University

of Technology and Economics, Budapest, Hungary

Keywords: Sensor signal processing, Sensor fusion, Home health monitoring.

Abstract: This paper presents a study how accelerometer sensors can be used to estimate speed and position by

integrating the sensor signals once and twice, respectively. Unfortunately, integration emphasises bias and

noise of the sensor. We developed a heuristic nonlinear filter which efficiently suppresses unwanted effects,

assuming human movement. Our aim is to provide a mobile sensor to detect the movement of elderly people

suffering from dementia, for home health monitoring purposes. Utilising this sensor together with others

allows us to detect unusual behaviour of the patient. The two accelerometer signals together with the

suggested heuristic nonlinear filtering allows us to reliable measure the speed, and reconstruct the shape of

the movement trajectory of the patient.

1 INTRODUCTION

There are many applications which require speed

and position measurement of an object with cheap

and mobile sensors, which do not obstruct the

movement. Our aim is to find an appropriate device

for home health monitoring, i.e. to track the

movement of elderly people in their home, suffering

from dementia. This, together with other sensors in

the home might be used to detect unusual behaviour

of the patient, and to warn the relatives or the

nurse/doctor. There are several types of information

which might be useful for this purpose. This

includes the current position of the patient in his/her

home (which room, which part of the room), speed

of the movement, acceleration (e.g. detecting a fall).

Even the shape of the trajectory of the movement is

useful information to detect whether the patient is

moving intentionally into a specific direction or

nervously perambulates, walks back and forth, or

circulates in the room.

One possibility to extract many of the above

features is to install cameras in every room of the

house. If two cameras per room are installed, even

precise 3 dimensional position reconstruction is

possible (Hartley and Zissermann, 2006), although

the image processing is not trivial (face recognition,

cloaking, more people in the room etc.). This

solution has the drawbacks that installation demand

and costs are high, and people are very much

dismissive about being watched, even if the image

itself is not viewed by others, only certain

characteristic parameters are extracted from the

images. Moreover, reliable information can be

retrieved only under certain lighting conditions. If

the room is not lit, e.g. at night, cameras cannot be

used.

Another possibility to detect position is to use

passive infra movement sensors in every room

(Scanaill et al., 2006). If more sensors are installed

in one room (e.g. into the four upper corners of

walls) not only a binary signal is provided (someone

resides in the room or not), but also the section

within the room can be detected. However, this is

still a very rough detection of the position, no other

information can be extracted from the measurement

and requires many wiring in the house, which might

bother the patient.

RFID is also a good idea (Mateska et al. 2011).

However, the range of the detection of RFID tags is

limited, thus many RFID readers have to be

installed, which increases the installation time and

cost, and the room would be full of wires. This

approach aims to detect only the position.

In this research we investigated the possibilities

of utilising accelerometer sensors to measure the

acceleration, and estimate the speed and position by

integrating the signals. The idea is to put the tiny

accelerometer into regularly worn clothes or even

350

Dabóczi T. and Kalvach A..

MOBILE SPEED AND POSITION SENSOR FOR HOME HEALTH MONITORING BASED ON ACCELEROMETER SIGNALS.

DOI: 10.5220/0003790603500354

In Proceedings of the International Conference on Biomedical Electronics and Devices (BIODEVICES-2012), pages 350-354

ISBN: 978-989-8425-91-1

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

better into the slipper. The collected signal can be

occasionally transmitted by wireless sensor network

to a gateway, to spare battery life. With this

approach we aim to provide information about the

acceleration and speed of the patient, and about the

shape of the trajectory of the movement. Precise

position estimation seemed to be impossible after

double integration; however, the shape of the

movement is reliable reconstructed. Integration

emphasises the bias and noise of the measurement

more and more as the time goes. With double

integration the effect is even stronger. Pure double

integration provides useless estimate. We developed

a nonlinear heuristic filter, which takes into account

that human movement has certain behaviours

(limited speed, acceleration, many times in still etc.).

2 DISTURBING EFFECTS

The speed and position information can be

reconstructed from the acceleration by integrating

the signal once and twice.

∫

= dttav )( ,

∫∫

= dtdttax )( ,

(1)

where x denotes the position, v denotes speed, a

denotes the acceleration and t stands for time. Since

the three dimensions in the space are independent,

position in the 2 or 3D space can be reconstructed by

independently integrating the different (orthogonal)

components. If the acceleration signal is available as

sampled data, we can estimate the integral by simple

accumulation of the samples:

[] []

[

][]

∑∑∑

Δ=Δ= iatixiativ

(2)

where [i] stands for the sampled version of the

corresponding signal and

tΔ denotes sampling

time. Here we assume equidistant sampling.

However, if the accelerometer sensor is not

perfect, we will integrate all biases and disturbances

also. We need to face offset error, gain error, offset

drift, wideband electric noise and quantization noise.

[] []

(

)

∑∑

+⋅Δ= eiaGtix

(3)

where G denotes gain error and e stands for all offset

like errors, including wide band electric and

quantization noise.

Offset-, gain error, offset drift and wideband

electric noise are caused by the sensor itself, while

quantization noise is produced by the AD converter.

We could model other disturbances of the AD

converter also, like e.g. integral nonlinearity,

however, using a small resolution ADC (8..10 bits)

these disturbances can be neglected compared to the

others. A short measurement of one of the two

independent 3D accelerometers is shown in Fig. 1.,

having still sensors. It can be observed that there is

quite a large noise on the signals. The two sensors –

each having 3 axes – have slightly different offset

and gain errors. The channel, showing around 9 m/s

corresponds approximately to the direction of the

gravity. (Sensors were not precisely positioned to

align with the horizontal and vertical directions.)

0 200 400 600 800 1000 1200 1400 1600

-12

-10

-8

-6

-4

-2

samples

a [m/sec

]

Figure 1: 3D accelerometer signals in still position.

We observed that offset error is always present,

and is characteristic to a particular sensor. Thus, we

can compensate for them after a short calibration

procedure. Unfortunately, offset error changes with

the temperature, thus a one time calibration remains

valid only until the temperature does not change

significantly. In our application we can assume that

room temperature does not change abruptly and

much, thus we do not compensate the sensor signal

for offset drift. Gain error can be compensated

utilizing offline calibration measurements.

Wide band electric noise and quantization noise

can be treated together. They all have the following

properties: they have a symmetric probability

density function with zero mean value, and they

have a wide and approximately white spectral

distribution. After integrating the acceleration signal

the variance of the speed estimate increases with the

square of time. After double integration the variance

of the position estimate is increased already with the

fourth power of time. Fig. 2 shows the first and

second integral of a Gaussian noise having

symmetric probability density function with zero

mean value.

In the remaining we will focus on compensating

the effect of the offset error and the noise.

MOBILE SPEED AND POSITION SENSOR FOR HOME HEALTH MONITORING BASED ON ACCELEROMETER

SIGNALS

351

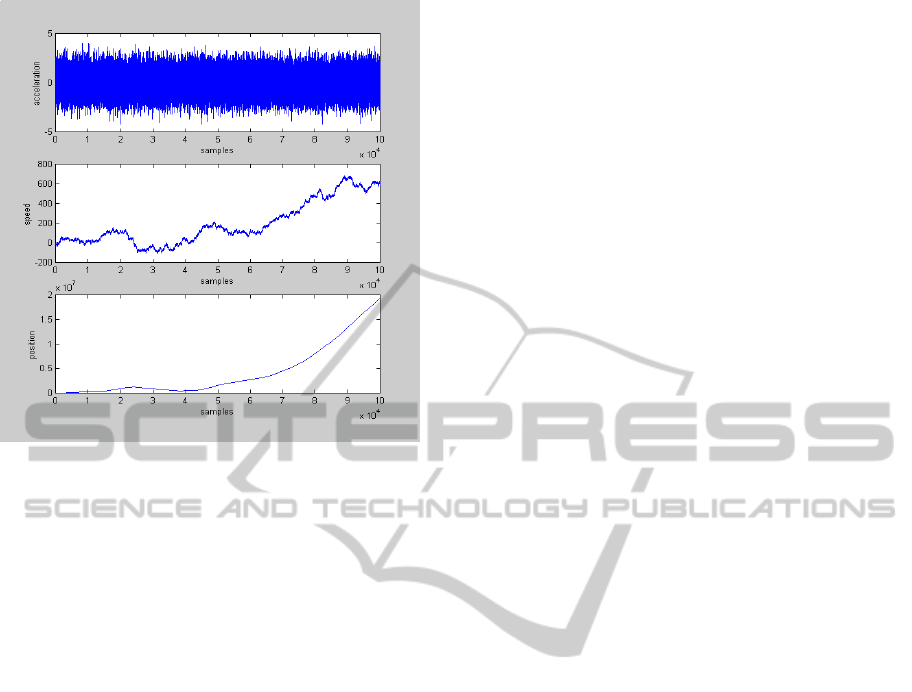
Figure 2: First- (middle figure) and second integral (lower

figure) of a Gaussian noise (upper figure).

3 HARDWARE SETUP OF THE

EXPERIMENT

In order to verify the behaviour of our position esti-

mator we set up a sensor system. Our department

developed a modular platform for embedded sys-

tems (Tóth et. al, 2005), which we used as a rapid

prototyping device. We integrated two accelerome-

ters to the 8 bit microcontroller system, each having

± 3g range in all 3 axes. This range seemed to

cover all acceleration resulted from the movement of

an elderly man/woman, taking into account that

gravity adds to the signal in one direction. The sen-

sor has a proportional analog output, thus we need a

6 channel AD converter to digitize the signals. The

ATMega128 microcontroller of the rapid prototyp-

ing system has a built in ADC, with 10 bits resolu-

tion. The sampling frequency is set to 162 Hz

(corresponding to ~6 msec sampling period for each

channel). The sampled acceleration signals can be

retrieved from the embedded system either through

wired serial port, or wireless link in the ISM

frequency band (433 MHz).

4 SPEED AND POSITION

ESTIMATION

The speed signal can be calculated from the

acceleration signal by means of integration, while

position with double integration. As we concluded in

the first section we can focus on offset error and

noises as the main disturbing effects of the

integration. First we will assume that the movement

is in a horizontal plane, and the sensor itself does not

rotate. Later in Section 5 and 6 we will investigate

the effect of the rotation and the gravity.

The offset error can theoretically be removed by

suppressing the DC component. Real time

suppression of the DC component with a very

narrow suppression band highpass filter would

require long FIR filter, which means on one hand a

large delay, on the other hand very large

computation demand. Here we were satisfied with

offline computation of a larger data set, carried out

in a PC, where data was collected regularly from the

embedded sensor system. In that case the constant

offset throughout the dataset was considered the

mean value of the record, which was removed from

the acceleration signals (each channel separately).

The noise can be handled in several ways. We

implemented two accelerometers, which provide

measurements from the same movement with

uncorrelated noise, and independent disturbances

(offset error, bias etc.). Our first attempt to reduce

the effect of the noise is to average the

corresponding channels of the two sensors. Cross

correlation of the same channel of the two sensors

proves that the noise can be treated as uncorrelated.

The noise variance is thus reduced.

The second attempt to reduce the effect of the

noise is an appropriate filtering. Human movement

has certain bandwidth. Thus, filtering out

components that are out of the supposed bands

reduces the noise variance. We tried to filter the

speed signal. Our concept is that human movement

has the characteristics that speed is zero in most of

the time. A very low speed motion is not realistic; it

will be handled as cause of error of integration.

Thus, we need to observe the baseline shift of the

speed signal, and compensate the speed

measurement for that.

4.1 Linear and Order Statistic Filtering

As the baseline we want to estimate has very low

frequency components first we applied a narrow-

band linear lowpass filter. However, this filtering

brought no satisfactory results. It is hard to sharply

separate the baseline and human movement. We

skipped this possibility.

Our second attempt to filter the speed signal was

an order statistic, nonlinear filter, namely the median

filter. It has the advantage that impulse like noises

can be efficiently removed. In that context short

BIODEVICES 2012 - International Conference on Biomedical Electronics and Devices

352

movements will be treated as “impulses”, and we

assume that the patient remains still most of the

time. The window size of the median filter needs to

be fitted to the possible length of the duration of the

movements (couple of seconds). This solution has

much better performance than linear filtering,

however, still not good enough.

400 600 800 1000 1200 1400

-0.06

-0.04

-0.02

0.02

0.04

samples

v [m/sec]

v ori ginal

v with noise

v baseli ne

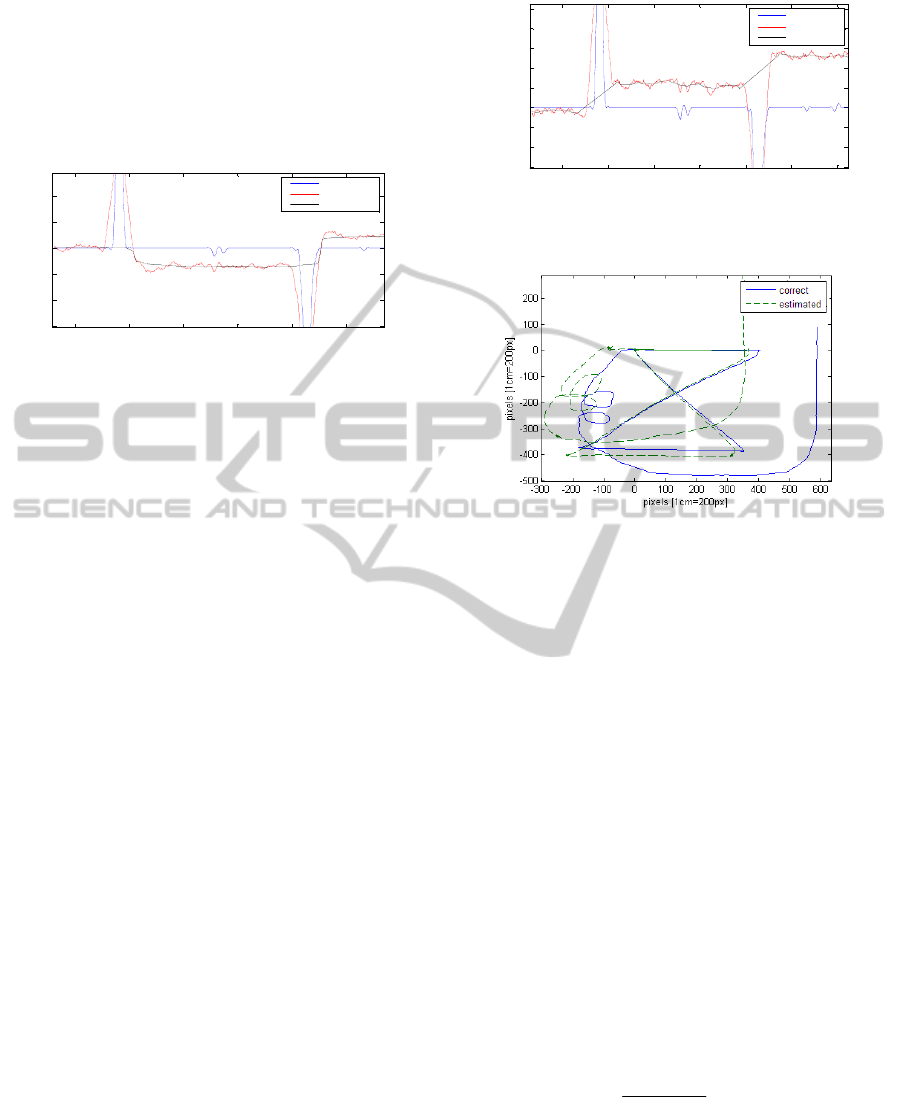
Figure 3: Baseline removal of the speed signal by means

of median filter.

4.2 Heuristic Nonlinear Filtering

We propose to use a heuristic nonlinear filter. The

main principle of the filter is that we are looking for

long parts of the signal which have nearly constant

speed. These parts will be considered as zero-speed

parts, and the deviation will be treated as

disturbance. Between the constant speed parts the

baseline will be linearly interpolated. This method

has the advantage over median filtering that we get

an acceptable estimate for the baseline even during

the movement, and the baseline estimate will be a

continual function.

Fig. 4 shows a simulation result with the

proposed filter. Recording the movement of the PC

mouse carried out the reference measurement. We

distorted this signal synthetically and added noise to

simulate the real environment. Position is

reconstructed with double integration after filtering

the speed signal. It can be observed that fractional

movements are much better reconstructed than

continuous one (Fig. 5). The shape of the trajectory

of the movement is reliable reconstructed, while the

2D position information is distorted after double

integration.

5 CORRECTION OF SENSOR

ROTATION

In the previous section we assumed a horizontal

movement, where the coordinate system of the

world and the sensor are aligned. If the sensor itself

rotates, this assumption is not valid any more. We

need to detect this situation and correct the signals

appropriately.

400 600 800 1000 1200 1400 1600

-0.03

-0.02

-0.01

0.01

0.02

0.03

0.04

0.05

samples

v [m/sec]

v origi nal

v with noise

v baseli ne

Figure 4: Baseline removal of the speed signal by means

of the proposed heuristic filter.

Figure 5: Position estimation in 2 dimensions.

We can make use of the fact that we have two

sensors of the same type. If there is no rotation, the

two sensors measure the same acceleration, apart

from bias and noise. If the sensors are rotated, there

will be a difference in the accelerations. Averaging

the two signals reduces the noise and provides an

acceleration estimate for the point in-between the

two sensors, and cancelling the effect of rotation.

Thus, we can separate acceleration and angular

acceleration.

Averaged signals depend only on acceleration,

while the difference of the two sensors depends only

on the angular acceleration, assuming that the axes

of the two sensors are aligned well enough. In this

case if the sensors are rotated with β angular

acceleration around the point halfway between the

two sensors, both sensors will measure an additional

acceleration component, perpendicular to the axes

connecting the sensors (Fig. 6.).

The angular acceleration can be calculated from

the two measurements as follows:

−

(4)

where

denotes the estimate of the angular

acceleration, a

and a

are the acceleration

components perpendicular to the axes connecting the

sensors, and r denotes the radius of rotation (half of

the distance between the sensors). After

MOBILE SPEED AND POSITION SENSOR FOR HOME HEALTH MONITORING BASED ON ACCELEROMETER

SIGNALS

353

compensating with this component we can use the

former methods to integrate the signals.

The accuracy can be increased by a stronger

lowpass filtering of the angular acceleration signal,

since it can be assumed that angular acceleration has

a very low frequency.

In a non-ideal case the two sensors cannot be

perfectly aligned in the space on the printed circuit

board, thus, there will be a mismatch in the direction

of the axes. This results a difference in the

acceleration signals of the two sensors even without

rotation. The observed “false” angular acceleration

depends on the acceleration and the angle between

the axes of the two sensors. The angle mismatch is

distorted by a trigonometric function (sin(x)). For

small angles the sine function might be

approximated by its argument. The angle mismatch

should be determined based on offline calibration

measurements. This should be done only once, after

the soldering of the sensor. However, knowing this

component means that the measured acceleration

needs to be compensated regularly with

a)sin(

Please note that in this case the axis x is the

“average” of the two axes of sensors.

Figure 6: Effect of the rotation of the sensors, together

with acceleration.

6 EFFECT OF GRAVITY

In the former sections we neglected the effect of

gravity as we assumed a horizontal motion. In the

case the sensors are not constantly moving in hori-

zontal plane, the gravity adds an extra acceleration

to the sensor signals. Fortunately these additional

accelerations are constant while the sensors are not

moving. The heuristic filter – which we have applied

on the speed signal – is designed for this case. Thus,

applying the same heuristic filter on the acceleration

signal can cancel the effect of gravity.

We can improve the gravity cancellation by us-

ing the rotation estimation. If we apply 3D acceler-

ometers, we can calculate a 3 dimensional rotation

and so the direction of gravity. After this the gravity

components can be subtracted from the signals. In

order to make a good gravity cancellation, the two

methods should be applied together.

7 CONCLUSIONS

In this paper we investigated the use of two

accelerometers to measure the acceleration and

estimate the speed and position of elderly people

suffering from dementia, for home health monitoring

purposes.

We developed a heuristic filter to suppress the

measurement disturbances, which would make the

estimate impossible because of the integration of the

raw signal data. We also developed an algorithm to

detect and correct for the rotation of the sensors.

Fabrication or installation mismatch of the axes of

acceleration sensors can also cause problem, for

which we developed also a compensation method.

Simulation and measurement experiments show

that speed estimate is quite reliable based on one

time integration, after utilising the proposed

heuristic nonlinear filter. Precise position estimate

not possible, however, in the case of fractal

movement the shape of the trajectory can be well

reconstructed, which is a useful information about

the patient.

ACKNOWLEDGEMENTS

This work has been supported by BelAmi and

Hungarian Scientific Research Fund (OTKA), grant

number TS-73496. Support of Bolyai János

Scholarship is also acknowledged.

REFERENCES

Hartley, R., Zissermann, A., 2006. Multiple View

Geometry in Computer Vision, Cambridge University

Press, second edition.

Tóth Cs, Simon Gy, Dabóczi T, Scherer B, Kádár L, Samu

G, Benesóczky Z, Péceli G, 2005. A modular Platform

for Embedded Information Technology. Proceedings

of DDECS: 8th IEEE Workshop on Design and Dia-

gnostics of Electronic Circuits and Systems. Sopron,

Hungary, 2005. April 13-16. pp. 198-201.

Scanaill, C. N., Carew, S., Barralon, P., Noury, N., Lyons,

D. and Lyons, G. M., 2006. A Review of Approaches

to Mobility Telemonitoring of the Elderly in Their

Living Environment, Annals of Biomedical Enginee-

ring, Volume 34, Number 4, pp. 547-563.

Mateska, A.; Pavloski, M.; Gavrilovska, L.; 2011, RFID

and Sensors Enabled In-Home Elderly Care, MIPRO

Conference 2011, May 23-27, 2011, Opatija, Croatia,

pp. 285-290.

BIODEVICES 2012 - International Conference on Biomedical Electronics and Devices

354