
EVALUATION OF NEGENTROPY-BASED CLUSTER VALIDATION
TECHNIQUES IN PROBLEMS WITH INCREASING
DIMENSIONALITY
L. F. Lago-Fern´andez, G. Mart´ınez-Mu˜noz, A. M. Gonz´alez and M. A. S´anchez-Monta˜n´es
Escuela Polit´ecnica Superior, Universidad Aut´onoma de Madrid, Madrid, Spain
{luis.lago, gonzalo.martinez, ana.marcos, manuel.smontanes}@uam.es
Keywords:
Clustering, Cluster validation, Model selection.
Abstract:
The aim of a crisp cluster validity index is to quantify the quality of a given data partition. It allows to select
the best partition out of a set of potential ones, and to determine the number of clusters. Recently, negentropy-
based cluster validation has been introduced. This new approach seems to perform better than other state of the
art techniques, and its computation is quite simple. However, like many other cluster validation approaches,
it presents problems when some partition regions have a small number of points. Different heuristics have
been proposed to cope with this problem. In this article we systematically analyze the performance of differ-
ent negentropy-based validation approaches, including a new heuristic, in clustering problems of increasing
dimensionality, and compare them to reference criteria such as AIC and BIC. Our results on synthetic data
suggest that the newly proposed negentropy-based validation strategy can outperform AIC and BIC when the
ratio of the number of points to the dimension is not high, which is a very common situation in most real
applications.
1 INTRODUCTION
Negentropy-based cluster validation has been recently
introduced (Lago-Fern´andez and Corbacho, 2010). It
aims at finding well separated and compact clusters,
and has a number of advantages such as the simplic-
ity of its calculation, which only requires the compu-
tation of the log-determinants of the covariance ma-
trices and the prior probabilities for each cluster. It
can deal satisfactorily with clusters with heteroge-
neous orientations, scales and densities, and has been
shown to outperform other classic validation indices
on a range of synthetic and real problems.
However, like many other cluster validation ap-
proaches (Gordon, 1998; Xu and II, 2005), negen-
tropy based validation presents difficulties when vali-
dating clustering partitions with very small clusters.
In these cases, the quality of the estimation of the
log-determinant of the covariance matrix involved in
the computation of the negentropy index can be very
poor, with a strong bias towards −¥ , as shown in
(Lago-Fern´andez et al., 2011). This can bias the vali-
dation index towards solutions with too many clusters
if no additional requirements, such as constraints on
the minimum number of points per cluster, are im-
posed. In the mentioned study this problem is for-
mally analyzed, and a correction to the bias is pro-
posed. A heuristic for cluster validation based on the
negentropy index is also introduced. This heuristic
takes into account the variance in the estimation of
the negentropy index, and allows to disregard cluster-
ing partitions with a low negentropy index but a high
variance.
In this work we propose a more formal heuris-
tic that refines the correction of the negentropy index
proposed in (Lago-Fern´andez et al., 2011) in order
to quantify the confidence levels of the index value.
Additionally, we improve their analysis studying the
performance of different negentropy based validation
approaches with respect to the number of dimensions.
In order to make a systematical test, we use a bench-
mark database that spams a broad range of dimen-
sions. This benchmark is based on the twonorm clas-
sification problem (Breiman, 1996). In order to inter-
pret our results in a proper context, we compare the
performance of the different negentropy-basedcluster
validation approaches with AIC (Akaike, 1974) and
BIC (Schwartz, 1978; Fraley and Raftery, 1998).
Our results on synthetic data show that, in general,
for low dimensions negentropy-based cluster valida-
tion performs well when there is not a high overlap
amongst the clusters. On the other hand, when the
F. Lago-Fernández L., Martínez-Muñoz G., M. González A. and A. Sánchez-Montañés M. (2012).
EVALUATION OF NEGENTROPY-BASED CLUSTER VALIDATION TECHNIQUES IN PROBLEMS WITH INCREASING DIMENSIONALITY.
In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 235-241
DOI: 10.5220/0003793602350241
Copyright
c
SciTePress

clusters are highly overlapped the BIC index can pro-
vide better results, as long as the number of points per
cluster is high enough. Note however that BIC is in-
tended for fitting distributions rather than for cluster-
ing, so it can deal well with the overlap. We also find
that, when the ratio of the number of points to the di-
mension is small, negentropy-based methods can out-
perform BIC. Given that this is usual in real applica-
tions, and given the simplicity in the calculation of
negentropy-based indices, we strongly encourage its
application for real clustering problems.
2 THE NEGENTROPY INDEX
Let us consider a random variable X in a d-
dimensional space, distributed according to the prob-
ability density function f(x). Let s = {x
1
,..., x
n
} be
a random sample from X, and let us consider a par-
tition of the space into a set of k non-overlapping re-
gions W = {w
1
,..., w
k
} that cover the full data space.
This partition imposes a crisp clustering structure on
the data, with k clusters each consisting of the data
points falling into each of the k partition regions. The
negentropy increment of the clustering partition W ap-
plied to X is defined as (Lago-Fern´andez and Corba-
cho, 2010):
D J(W ,X) =
1
2
k
å
i=1
p
i
log|S
i
|−
k
å
i=1
p
i
log p
i
(1)
where p
i
and S
i
are the prior probability and covari-
ance matrix respectively for X restricted to the region
w
i
. The negentropy increment is a measure of the
average normality that is gained by making a parti-
tion on the data. The lower the value of D J(W ), the
more Gaussian the clusters are on average, therefore
the rule for cluster validation is to select the parti-
tion that minimizes the negentropy increment index.
Of course, in any practical situation we do not have
knowledge of the full distribution of X, and we have
to estimate the negentropy increment from the finite
sample s. A straightforward estimation can be done
using the index:
D J
B
(W ,s) =
1
2
k
å
i=1
˜p
i
log|
˜
S
i
|−
k
å
i=1
˜p
i
log ˜p
i
(2)
where ˜p
i
and
˜
S
i
are the sample estimations of p
i
and S
i
respectively. The subindex B has been intro-
duced to emphasize that this estimation of the negen-
tropy increment is biased due to a wrong estimation
of the terms involving the log-determinants (Lago-
Fern´andez et al., 2011). This bias can be corrected
using the expression:
D J
U
(W ,s) = D J
B
(W ,s) +
1
2
k
å
i=1
˜p
i
C(n
i
,d) (3)
where C(n
i
,d) is a correction term for the log-
determinant which depends only on the number of
sample points in region i, n
i
, and on the dimension
d (Misra et al., 2005):
C(n
i
,d) = −d log
2
n
i
−1
−
d
å
j=1
Y (
n
i
− j
2
) (4)
Here Y is the digamma function (Abramowitz and
Stegun, 1965). It can be shown that this new estimator
is unbiased, that is:
E[D J
U
(W ,s)]
s
= D J(W ) (5)
And that the variance of D J
U
(W ,s) can be estimated
as:
s
2
s
(D J
U
) ≈
1
4
k
å
i=1
˜p
2
i
d
å
j=1
Y
′
(
n
i
− j
2
) (6)
where Y
′
is the first derivative of the digamma func-
tion, also known as trigamma function. Different uses
of these results lead to the different validation ap-
proaches presented in the following section.
3 VALIDATION APPROACHES
3.1 Negentropy-based Approaches
The general rule for cluster validation based on the
negentropy increment is that, given a set of clustering
partitions P = {W
1
,..., W
M
} on a given problem de-
fined by the random variable X, one should select the
partition W
i
for which D J(W
i
) is minimum. That is:
D J(W
i
) ≤D J(W
j
) ∀W
j
∈P
This means that the clusters resulting from W
i
are,
on average, more Gaussian than those resulting from
any other partition in P . In practical terms, we
never know the values D J(W
i
), but only estimations
obtained from a finite sample s. The different ap-
proximations shown in section 2 lead to the following
approaches.
Biased Index. The first possibility is to use the
estimation D J
B
(W ,s) in equation 2. Minimization of
D J
B
over P will lead to the validated partition.
Unbiased Index V1. A second approach is to
consider the estimation D J
U
(W ,s) in equation 3. As
before, minimization of D J
U
over P will lead to the

validated partition.
Unbiased Index V2. The direct minimization of the
corrected index D J
U
(W ,s) does not take into account
the variance in the estimation due to the finite sam-
ple size. So it could happen that, for two given par-
titions W
1
and W
2
, the true values of the negentropy
increment satisfy D J(W
1
) < D J(W
2
), while their sam-
ple estimations satisfy D J
U
(W
1
,s) > D J
U
(W
2
,s). To
minimize this effect we follow here the approach in
(Lago-Fern´andez et al., 2011) and consider the two
partitions equivalent if:
D J
U
(W
2
,s) + s
s
(D J
U
(W
2
)) <
D J
U
(W
1
,s) −s
s
(D J
U
(W
1
)) (7)
In such cases we select the simplest (lower number
of regions) partition. We will refer to this approach
as D J
US
.
Unbiased Index V3. If we make the assumption
that the real D J(W ) is normally distributed around
D J
U
(W ,s) with variance s
2
s
(D J
U
), we can estimate the
probability that D J(W
1
) < D J(W
2
) by:
P(D J(W
1
) < D J(W
2
)) =
Z
¥
−¥
dxf
2
(x)F
1
(x) (8)
where f
i
(x) and F
i
(x) are, respectively, the probability
and cumulative density functions of a random Gaus-
sian variable X ∼ N(D J
U
(W
i
,s), s
s
(D J
U
)). Then we
can consider the two partitions equivalent if P is lower
than a given threshold a . In such a case we must pro-
ceed as before and select the simplest partition. We
will consider a = 0.8, and will refer to this approach
as D J
UG
.
3.2 Reference Approaches
We will consider two additional criteria based on in-
formation theoretic approaches: the Akaike Informa-
tion Criterion, AIC (Akaike, 1974), and the Bayesian
Information Criterion, BIC (Schwartz, 1978; Fraley
and Raftery, 1998). Both of them are intended to mea-
sure the relative goodness of fit of a statistical model
by introducing a penalty term to the log-likelihood,
and have been extensively used to determine the num-
ber of clusters in model-based clustering. It is known
that, when fitting a statistical model to a data sample,
it is possible to arbitrarily increase the log-likelihood
by increasing the complexity of the model, but doing
so may result in overfitting. AIC and BIC are defined
as follows:
AIC = 2p −2log(L)
BIC = plog(n) −2log(L)
where p is the number of free parameters in the sta-
tistical model, n is the sample size and L is the log-
likelihood for the model. Both methods reward the
goodnessof fit of the model, but also include a penalty
term that is an increasing function of the number of
free parameters. In both cases the preferred model is
the one with the smallest AIC or BIC value.
4 DATA SETS
4.1 Gaussian Clusters in 2D
We use a set of two-dimensional clustering prob-
lems generated as in (Lago-Fern´andez and Corba-
cho, 2010). Each problem consists of c clusters, with
each cluster containing 200 points randomly extracted
from a bivariate normal distribution whose means and
covariance matrices are also randomly selected. We
consider c in the range [1,9], and generate 100 prob-
lems for each c.
4.2 Twonorm Problems
The twonorm problem is a synthetic problem ini-
tially designed for classification (Breiman, 1996).
Given that the classes of the problem are known it
also constitutes a good benchmark for testing clus-
tering algorithms. It is a d-dimensional problem
where each class is extracted from a d-variate nor-
mal distribution with identity covariance matrix and
mean located at (a,a,...,a) for class/cluster 1 and
at (−a,−a,...,−a) for class/cluster -1, where a =
2/
√
20. The optimal separation plane is the hyper-
plane which passes through the origin and whose nor-
mal vector is (a, a,...,a). The problem is designed
such that the Bayes error is constant (≈0.023) and in-
dependent of the dimension d. Here we consider even
dimensions in the range [2,20], and generate 1000
points for each cluster.
5 ANALYSIS
5.1 Clustering Algorithm
For a given problem, we use the Expectation-
Maximization (EM) algorithm to fit a mixture of k
Gaussian components to the data. Different number
of components are tried, and a total of 20 different
runs of the algorithm are performed for each k. Af-
ter convergence of the algorithm, a crisp partition of
the data is obtained by assigning each data point to a
0 1 2 3 4 5 6 7 8 9 10
−0.05
0
0.05
0.1
0.15
0.2
0.25
0.3
number of clusters
maximum overlap
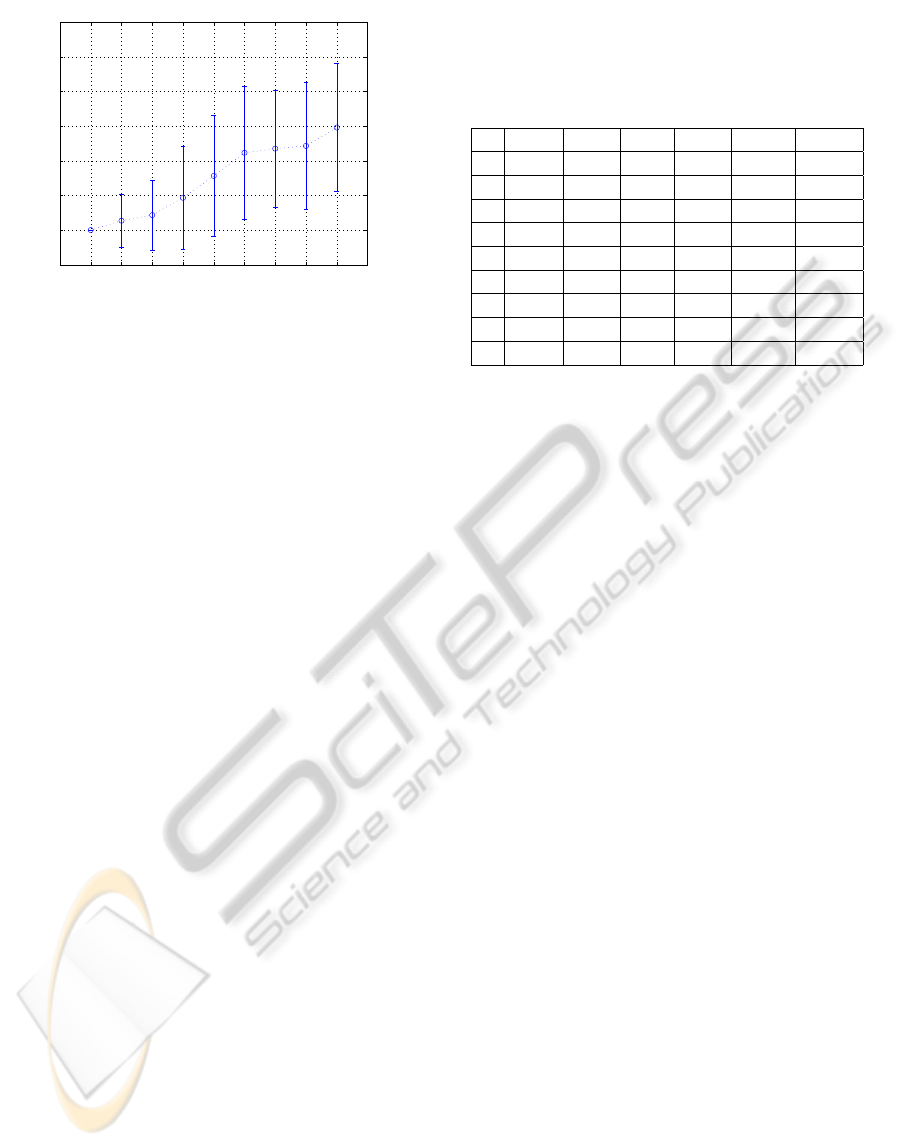
Figure 1: Maximum overlap between pairs of clusters ver-
sus number of clusters c for the Gaussian 2D problems. For
a given c the average over 100 problems and its standard
deviation are shown.
single cluster, represented by the mixture component
that most likely explains it. For the 2D Gaussian prob-
lems we consider k ∈ {1, ...,13}. For the twonorm
problems we consider k ∈ {1,..., 4}. This means that
we end up with a set of 260 different clustering par-
titions (only 80 for the twonorm problems) that must
be validated in a subsequent stage. This validation is
performed using each of the 6 approaches described
in section 3. Each approach leads to a single selected
partition for each of the problems.
5.2 Evaluation of the Results
To measure the quality of a validated partition, and
extensively the quality of a given validation approach,
we compare the number of regions in the partition
with the real number of clusters in the problem. We
consider the number of problems for which a given
validation approach provides a partition into the cor-
rect number of regions. Additionally, in some cases
we also compute the average number of regions to
have an idea of whether the validation index tends to
under or over-estimate the number of clusters.
Finally, in order to measure the intrinsic difficulty
of a given clustering problem, we consider the max-
imum overlap between any two clusters in the prob-
lem. We measure the overlap between two clusters
as the Bayes error for a two-class classification prob-
lem where each cluster is one class. For the Gaussian
2D problems, this overlap increases with the number
of clusters because the total amount of space is fixed
(see figure 1). The twonorm problem, on the other
hand, is designed such that the Bayes error is con-
stant (≈ 0.023) and independent of the dimension, so
all the problems have in this case the same intrinsic
difficulty.
Table 1: Gaussian problems in 2D. Number of problems
correctly validated by each of the six validation approaches
considered. The first column, c, represents the actual num-
ber of clusters. The number of problems for a given c is
100.
c AIC BIC D J
B
D J
U
D J
US
D J
UG
1 48 99 72 88 100 100
2 5 91 11 24 84 95
3 1 91 10 21 75 91
4 1 83 3 20 66 84
5 2 79 9 20 46 61
6 3 83 10 17 37 45
7 3 72 13 13 24 35
8 5 66 12 17 29 32
9 3 42 16 18 16 16
6 RESULTS
6.1 Gaussian Clusters in 2D
In table 1 we show the number of problems for which
each validation technique provides the correct num-
ber of clusters. Each row shows the results for a given
number of real clusters in the problem. There are 100
different problems for each number of clusters, there-
fore the maximum possible value in the table is 100.
We see that the negentropy-based approaches D J
US
and D J
UG
outperform the classical BIC index only for
problems with a small number of clusters (c ≤4). Of
these, the D J
UG
provides slightly better results. The
BIC index is the best for high number of clusters. The
D J
B
, D J
U
and AIC indices perform very poorly for all
the problems.
In table 2 we show the average number of clus-
ters for the solutions selected by each of the methods.
Note that, in spite of finding a correct solution in more
occasions, BIC presents a stronger tendency to over-
estimate the number of clusters when it fails. In such
a situation, the indices D J
US
and D J
UG
tend to under-
estimate the number of clusters. From a clustering
perspective, this kind of error is in more accordance
with intuition: it seems more plausible to merge two
highly overlapping clusters than to split a single clus-
ter into two components. It was shown in figure 1
that the maximum overlap increases with the number
of clusters. This could explain the observed loss of
performance of D J
US
and D J
UG
with increasing c. Fi-
nally, the D J
B
, D J
U
and AIC indices tend to overesti-
mate the number of clusters even in the low overlap
regime.
In figure 2 we show how the overlap is distributed,
both for the correctly and the incorrectly validated

Table 2: Gaussian problems in 2D. Average number of clusters in the validated partitions for each of the six validation
approaches considered. The column labeled c shows the actual number of clusters.
c AIC BIC D J
B
D J
U
D J
US
D J
UG
1 2.5 ± 1.7 1.0 ± 0.2 1.8 ± 1.4 1.4 ± 1.1 1.0 ± 0.0 1.0 ± 0.0
2 4.7 ± 1.2 2.1 ± 0.6 4.0 ± 1.7 3.3 ± 1.6 1.8 ± 0.4 1.9 ± 0.2
3 6.0 ± 1.0 3.1 ± 0.4 4.9 ± 1.6 4.3 ± 1.5 2.7 ± 0.5 2.9 ± 0.3
4 6.8 ± 1.1 4.0 ± 0.5 6.2 ± 1.8 5.3 ± 1.7 3.6 ± 0.7 3.8 ± 0.4
5 7.6 ± 1.1 4.9 ± 0.4 6.5 ± 2.0 5.8 ± 1.8 4.3 ± 0.9 4.5 ± 0.6
6 8.8 ± 1.2 5.8 ± 0.4 7.6 ± 2.0 7.2 ± 1.7 5.0 ± 0.9 5.3 ± 0.8
7 9.7 ± 1.1 6.8 ± 0.6 8.6 ± 2.1 7.8 ± 1.8 5.8 ± 1.0 6.1 ± 0.9
8 10.8 ± 1.2 7.8 ± 0.8 9.9 ± 2.0 9.1 ± 1.9 6.9 ± 1.3 6.7 ± 1.2
9 11.7 ± 1.2 8.8 ± 1.0 10.2 ± 2.2 9.6 ± 2.0 7.6 ± 1.5 7.4 ± 1.1
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4
0
20
40
60
80
100
BIC
overlap
# occurrences
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4
0
20
40
60
80
100
Negentropy
overlap
# occurrences
Figure 2: Distribution of overlaps for correctly (black filled)
and incorrectly (white filled) validated problems by each of
the two methods BIC (top) and D J
UG
(bottom). The highest
bars have been truncated for the sake of clarity.
problems by each of the two methods BIC (top) and
D J
UG
(bottom). The distributions for D J
US
are similar
to those for D J
UG
(not shown). Observe that D J
UG
is
able to assess the correct number of clusters only for
small overlap. The number of failures is also reduced
in this small overlap region. This is in clear contra-
diction with the observation for BIC, which is able to
find the correct partition even in high overlap regimes.
If we recompute the values shown in table 1 tak-
ing into account only the problems whose maximum
overlap is below a given threshold t, we obtain the re-
sults shown in table 3. The value of the threshold has
been fixed to t = 0.03. The column labeled NP shows
the number of problems that satisfy this restriction for
a given c. Note that now there is almost no difference
between the results provided by BIC and D J
UG
.
Table 3: Gaussian problems in 2D. Number of problems
correctly validated by each of the six validation approaches
considered. Only problems with overlap lower than t = 0.03
are considered. The column labeled NP shows the number
of problems that satisfy this constraint for a given c.
c NP AIC BIC D J
US
D J
UG
1 100 48 99 100 100
2 86 2 78 75 86
3 79 1 72 65 79
4 63 0 54 50 62
5 42 0 40 32 40
6 28 1 27 19 24
7 12 0 10 7 10
8 16 1 14 12 12
9 7 0 4 4 3
Table 4: Twonorm problems. Number of problems correctly
validated by each of the six validation approaches consid-
ered. The first column, d, indicates the dimensionality of
the problem. The number of problems for a given d is 100.
d AIC BIC D J
B
D J
U
D J
US
D J
UG
2 31 100 80 89 100 100
4 5 100 38 55 100 100
6 1 100 2 10 100 100
8 0 100 0 2 100 100
10 0 9 0 0 100 100
12 0 0 0 0 100 100
14 0 0 0 0 100 100
16 0 0 0 0 100 97
18 0 0 0 0 93 81
20 7 0 0 0 62 76
6.2 Twonorm Problems
The twonorm problems considered here present an
overlap of approximately 0.023. This falls below
the threshold t = 0.03 used previously to filter high
Table 5: Twonorm problems. Average number of clusters in the validated partitions for each of the six validation approaches
considered. The first column shows the dimensionality of the problem.
d AIC BIC D J
B
D J
U
D J
US
D J
UG
2 3.0±0.8 2.0±0.0 2.3±0.8 2.1 ±0.4 2.0±0.0 2.0 ±0.0
4 3.6±0.6 2.0 ±0.0 2.8±0.7 2.6±0.7 2.0±0.0 2.0±0.0
6 3.8±0.4 2.0 ±0.0 3.6±0.5 3.4±0.7 2.0±0.0 2.0±0.0
8 3.8±0.4 2.0 ±0.0 3.9±0.3 3.6±0.5 2.0±0.0 2.0±0.0
10 3.7±0.4 1.1±0.3 4.0 ±0.1 3.8±0.4 2.0±0.0 2.0±0.0
12 3.8±0.4 1.0±0.0 4.0 ±0.0 4.0±0.2 2.0±0.0 2.0±0.0
14 3.8±0.4 1.0±0.0 4.0 ±0.0 4.0±0.1 2.0±0.0 2.0±0.0
16 3.6±0.5 1.0±0.0 4.0 ±0.0 4.0±0.0 2.0±0.0 2.0±0.2
18 3.4±0.5 1.0±0.0 4.0 ±0.0 4.0±0.0 2.1±0.3 2.2±0.4
20 3.2±0.5 1.0±0.0 4.0 ±0.0 4.0±0.0 2.4±0.5 2.2±0.4
overlap problems, which means that the two clusters
are quite well separated. The difficulty in this case
arises from the high dimensionality. The results for
these problems are shown in tables 4 and 5. The
first column in both tables is the dimension. Table 4
shows the number of problems for which each of the
validation methods provides a solution with 2 clus-
ters. Table 5 shows the average number of clusters in
the assessed solutions. All the validation approaches
show a loss of performance when the dimension of the
problems increases, but the D J
US
and D J
UG
indices
are more robust than the others. BIC starts to fail at
d = 10, experimenting a sudden loss of accuracy. For
higher dimensions it tends to select one single cluster.
On the other hand, D J
US
and D J
UG
are very accurate
even for d = 16, and their loss of accuracy for higher
dimensions is more gradual. Finally, the D J
B
, D J
U
and
AIC approaches provide very poor results, and show
a strong tendency to overestimate the number of clus-
ters.
7 CONCLUSIONS
The aim of this paper was to systematically study
the performance of negentropy-based cluster valida-
tion in synthetic problems with increasing dimension-
ality. Negentropy-based indices are quite simple to
compute, as they only need to estimate the probabil-
ities and the log-determinants of the covariance ma-
trices for each cluster. However, the computation of
the log-determinants in regions with small number of
points introduces a strong bias that must be corrected
in order to properly estimate the negentropy index. A
heuristic based on a formal analysis of the bias can be
obtained to alleviate this effect.
In this paper we refined the correction of the ne-
gentropy index proposed in (Lago-Fern´andez et al.,
2011) in order to quantify the confidence levels of
the index value, thus obtaining a new, more formal
heuristic for the validation of clustering partitions.
Then we studied the performance of this and other
negentropy-based validation approaches in problems
with increasing dimensionality, and compared the re-
sults with two well established techniques such as
BIC and AIC. The performance of BIC in problems
where the ratio of the number of points to the di-
mension is high, is quite good. For problems where
there are clusters with a high overlap, it clearly out-
performs the negentropy-based indices. This was ex-
pected since BIC is optimal for Gaussian clusters,
which is the case for the synthetic data considered
here. The AIC criterion seems to produce very bad
results for the set of problems considered, providing a
strong overestimation of the number of clusters in all
the cases. Negentropy-based indices are designed for
crisp clustering, and they seek to detect compact and
well separated clusters. When we consider only prob-
lems where the clusters are not highly overlapped, the
performances of BIC and the negentropy-based index
are quite similar.
In order to test the behavior of the indices as
a function of the dimensionality, we constructed
a clustering benchmark database based on the
twonorm classification problem (Breiman, 1996).
This database is generated using two Gaussian clus-
ters of increasing dimensionality but constant degree
of overlap. The number of points in each cluster is
constant independently of the dimension. Therefore,
the effect of the dimensionality on the performance
of the indices is isolated. As the dimensionality in-
creases, the performance of BIC degrades quickly,
but the performance of the negentropy-based index
is quite stable, finding the correct solution for all the
problems up to d = 16, and experimenting a gradual
degradation for higher dimension.
In conclusion we showed, using the synthetic
database twonorm, that our approach to negentropy-

based validation can outperform AIC and BIC in
problems where the ratio of the number of points
to the dimension is not high, which is a very com-
mon situation in most real applications. New exper-
iments with other databases are required in order to
check if this property is general. We expect that this
finding will be more accentuated in benchmarks with
non Gaussian clusters (Biernacki et al., 2000; Lago-
Fern´andez et al., 2009). This will be the subject of
future work.
ACKNOWLEDGEMENTS
The authors thank the financial support from DGUI-
CAM/UAM (Project CCG10-UAM/TIC-5864).
REFERENCES
Abramowitz, M. and Stegun, A. (1965). Handbook of math-
ematical functions. Dover, New York.
Akaike, H. (1974). A new look at the statistical model iden-
tification. IEEE Trans. Automatic Control, 19:716–
723.
Biernacki, C., Celeux, G., and Govaert, G. (2000). Assess-
ing a mixture model for clustering with the integrated
completed likelihood. IEEE Trans. Pattern Analysis
Machine Intelligence, 22(7):719–725.
Breiman, L. (1996). Bias, variance, and arcing classifiers.
Technical Report 460, Statistics Department, Univer-
sity of California, Berkeley, CA, USA.
Fraley, C. and Raftery, A. (1998). How many clusters?
which clustering method? answers via model-based
cluster analysis. Technical Report 329, Department
of Statistics, University of Washington, Seattle, WA,
USA.
Gordon, A. (1998). Cluster validation. In Hayashi, C.,
Ohsumi, N., Yajima, K., Tanaka, Y., Bock, H., and
Baba, Y., editors, Data science, classification and re-
lated methods, pages 22–39. Springer.
Lago-Fern´andez, L. F. and Corbacho, F. (2010). Normality-
based validation for crisp clustering. Pattern Recogni-
tion, 43(3):782–795.
Lago-Fern´andez, L. F., S´anchez-Montan´es, M. A., and Cor-
bacho, F. (2009). Fuzzy cluster validation using the
partition negentropy criterion. Lecture Notes in Com-
puter Science, 5769:235–244.
Lago-Fern´andez, L. F., S´anchez-Montan´es, M. A., and Cor-
bacho, F. (2011). The effect of low number of points
in clustering validation via the negentropy increment.
Neurocomputing, 74(16):2657–2664.
Misra, N., Singh, H., and Demchuk, E. (2005). Estimation
of the entropy of a multivariate normal distribution.
Journal of Multivariate Analysis, 92(2):324–342.
Schwartz, G. (1978). Estimating the dimension of a model.
Annals of Statistics, 6:461–464.
Xu, R. and II, D. W. (2005). Survey of clustering algo-
rithms. IEEE Trans. Neural Networks, 16(3):645–678.
