
CLUSTERING COMPLEX MULTIMEDIA OBJECTS
USING AN ENSEMBLE APPROACH
Ana Isabel Oviedo
1
and Oscar Ortega
2
1
Computer Department, Universidad Pontificia Bolivariana, Medellin, Colombia
2
System Engineering Department, Universidad de Antioquia, Medellin, Colombia
Keywords:
Complex multimedia objects, Clustering, Ensemble methods, Unsupervised learning.
Abstract:
A complex multimedia object is an information unit composed by multiple media types like text, images,
audio and video. Applications related with huge sets of such objects exceed the human capacity to synthesize
useful information. The search for similarities and dissimilarities among objects is a task that has been done
through clustering analysis, which tries to find groups in unlabeled data sets. Such analysis applied to complex
multimedia object sets has a special restriction. The method must analyze the multiple media types present
in the objects. This paper proposes a clustering ensemble that jointly assesses several media types present in
this kind of objects. The proposed ensemble was applied to cluster webpages, constructing a text and image
clustering prototypes. The Hubert’s statistic was used to evaluate the ensemble performance, showing that the
proposed method creates clustering structures more similar to the real classification than a joint-feature vector.
1 INTRODUCTION
A complex multimedia object (CMO) is an aggrega-
tion of heterogeneous data as a single unit. A CMO
is composed by multiple media types like text, im-
ages, audio and video (Hunter and Choudhury, 2003)
(Yang et al., 2008) (Zhuang et al., 2008). CMOs are
present in several scenarios like web sites, music al-
bums, electronic journals, electronic books, digitally
recorded sound, digital moving images, digital tele-
vision and social networks (Hunter and Choudhury,
2003) (Kriegel et al., 2008).
In applications with large amount of CMOs, the
huge number and the complexity of the relation-
ships among the objects exceed the human capac-
ity to analyze and synthesize useful information and
knowledge. The relationships among the objects can
be expressed by similarities and dissimilarities that
are searched in an automatic way using computers.
The search for similarities and dissimilarities among
CMOs is a task that has been done through clustering
analysis, whose goal is to find natural groups in an un-
labeled object set, such that objects in a group must be
similar or related to one another, and must be differ-
ent from the objects in other groups (Jain et al., 1999)
(Romesburg, 2004) (Dy and Brodley, 2004) (Alger-
gawy et al., 2008) (Jain, 2010). Humans are excel-
lent seekers in two or three dimensional problems, but
an automatic algorithm is necessary for higher dimen-
sions (Jain, 2010).
Formally, the clustering task has an input set of n
objects called X = {x
1
,x
2
,...,x
n
}, where each x
i
is a
feature vector of order d that represents the informa-
tion of object i with x
i
= ( f
1
, f
2
,..., f
d
) ∈ R
d
; each f
l
is
the lth feature. A clustering method attempts to dis-
tribute X into k groups given by C = {c
1
,c
2
,...,c
k
},
where k is the number of clusters with k ≤ n and c
j
represents the jth cluster.
A clustering analysis can be performed in different
ways. The literature review shows several clustering
approaches such as hierarchical, partitioning, fuzzy,
neural networks, probabilistic, graphs, evolutionary,
kernels and spectral methods. Yet, when cluster anal-
ysis is applied to CMO sets, it has a special restriction:
the method must analyze different media types. In the
clustering approaches reviewed so far for this study,
some methods combine multiple clustering structures
when sets whose elements have the same media type
are too complex to yield a unique clustering structure.
Such methods are called alternative clustering, clus-
tering aggregation, clustering ensemble and collabo-
rative clustering.
In support of a clustering for CMOs, this paper
proposes an ensemble approach which allows an in-
dependent clustering analysis of different media types
present in this kind of objects and then the results are
134
Isabel Oviedo A. and Ortega O. (2012).
CLUSTERING COMPLEX MULTIMEDIA OBJECTS USING AN ENSEMBLE APPROACH.
In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 134-143
DOI: 10.5220/0003794501340143
Copyright
c
SciTePress

combined with a voting function.
The paper outline is presented below. Section 2
presents the clustering lifecycle; section 3 presents
the literature review; section 4 presents the proposed
clustering ensemble; section 5 presents an evaluation
of the ensemble and, finally, the conclusions are pre-
sented in section 6.
2 CLUSTERING LIFECYCLE
This section describes the clustering lifecycle for ad-
dressing the proposed clustering ensemble. The pro-
cess of partitioning objects into clusters involves the
following stages: feature subset selection, similarity
measuring, clustering or grouping, cluster evaluation
and result interpretation. The flowchart in figure 1
shows a feedback in the process depending on the
cluster quality.
Figure 1: The clustering lifecycle.
The first stage, feature subset selection, involves
the attribute extraction that describes each object x
i
=
( f
1
, f
2
,..., f
d
). The goal of this stage is to find the
smallest feature subset that uncovers natural clusters
(Dy and Brodley, 2004). The feature subset selec-
tion can be performed with two approaches: filter or
wrapper algorithms (Dy and Brodley, 2004). The fil-
ter approach pre-selects the features before applying
a clustering method. The wrapper approach incorpo-
rates feature selection into the clustering method.
The second stage, similarity measuring, is not
easy to specify if the user does not have prior knowl-
edge about the objects (Fred and Jain, 2005) (Francois
et al., 2006). The goal of this stage is to specify how
to measure the similarity between objects, which can
be performed with two approaches: based on a prob-
ability distribution or based on a distance function.
The most used approach is similarity measuring based
on an Euclidean distance function; however, there are
other distance measures as cosine, manhattan, cheby-
shev, mahalanobis, minkowski and hamming, which
can produce diverse partitions for the same object set
(Fred and Jain, 2005).
The third stage, grouping, involves the applica-
tion of a clustering method using similarity measur-
ing. The goal of this stage is to partition an object set
X = {x
1
,x
2
,...,x
n
} into k groups. The grouping stage
can be performed with different approaches (Xu and
Wunsch, 2005) like hierarchical, partitional, fuzzy,
neural networks, probabilistic, graph, evolutionary,
kernel and spectral methods.
The fourth stage, cluster evaluation, measures the
quality of the partition obtained by the grouping stage
(Fred and Jain, 2005) (Jain, 2010). There are two
index approaches to evaluate cluster quality: exter-
nal validation and internal validation. External val-
idation evaluates the cluster quality based on a pre-
specified clustering structure. Some external indexes
are Rand, Fowlkes and Mallows, Hubert and Ara-
bie, and Jaccard (Halkidi et al., 2002)(Hashimoto
et al., 2009). Internal validation evaluates the cluster
quality based on compactness and separability mea-
sures; the compactness expresses how similar ob-
jects are in the same cluster and the separability ex-
presses how distinct objects are in different clusters.
Some internal indexes are Dunn, Davies-Bouldin, Sil-
houette, Gath-Geva, Fukuyama-Sugeno and Xie-Beni
(Halkidi et al., 2002)(Hashimoto et al., 2009).
The final stage, results interpretation, is one of the
most important steps. Its goal is to provide mean-
ingful information for users from the original objects
with a compact description of each cluster. The in-
terpretation of results can be performed in terms of
cluster prototypes or of the most representative ob-
jects such as the centroid (Jain et al., 1999).
3 THE LITERATURE REVIEW
The literature review shows several clustering ap-
proaches (Xu and Wunsch, 2005) (Filippone et al.,
2008) (Jain et al., 1999) (Jain, 2010), such as hier-
archical, partitioning, fuzzy, neural networks, prob-
abilistic, graphs, evolutionary, kernels and spectral
methods. Yet, other kinds of methods are used when
the dataset is too complex to yield a unique clustering
structure. Such methods combine multiple clustering
structures and have been applied to sets with the same
media type.
The following literature review was organized in
two parts: approaches for combining multiple cluster-
CLUSTERING COMPLEX MULTIMEDIA OBJECTS USING AN ENSEMBLE APPROACH
135

ing structures and clustering analysis applied to sets
with the same media type.
3.1 Approaches for Combining Multiple
Clustering Structures
Several approaches for combining multiple clustering
structures have been formulated based on the idea that
efficiency and accuracy can be increased by assess-
ing different clustering structures (Strehl and Ghosh,
2003) (Gancarski and Wemmert, 2007). The clus-
terers combination is considered more difficult than
classifiers combination in supervised learning, be-
cause the different clustering structures may not have
the same number of groups and there is no informa-
tion about the correspondence between the clusters of
the different clustering structures (Strehl and Ghosh,
2003) (Gancarski and Wemmert, 2007). In the litera-
ture review, different approaches have been found for
combining multiple clustering structures as altenative
clustering, clustering aggregation, clustering ensem-
ble and collaborative clustering.
3.1.1 Alternative Clustering
The first approach, called alternative clustering, gen-
erates different clustering structures and lets the user
select the best structure according to his/her need. In
(Caruana et al., 2006), the method is called meta-
clustering: they organize together many base-level
clusterings into a clustering of clusterings; thus the
user navigates to the clustering(s) useful for his/her
purposes. In (Bae and Bailey, 2006), the alternative
clustering structures start from an existing structure
and, in (Davidson and Qi, 2008), the use of con-
straints to characterize an existing clustering is pro-
posed and then an alternative solution can be gener-
ated.
3.1.2 Clustering Aggregation
The second approach, called clustering aggregation,
creates different clustering structures on the same
dataset and the final result is obtained by selecting
clusters among the structures. In (Law et al., 2004), a
method called Multi-objective clustering is proposed,
which applies several clustering algorithms corre-
sponding to different objective functions and then the
method picks the best set of objective functions for
creating the final clustering structure. Another clus-
tering aggregation approach is called Multi-run (Ji-
amthapthaksin et al., 2009), where the final cluster-
ing structure is a combination of high-quality clusters
created from multiple runs; the goal is the parameter
selection of a clustering algorithm.
3.1.3 Clustering Ensemble
The third approach, called clustering ensemble, com-
bines multiple partitionings of the same object set
without accessing the original features that deter-
mined the partitioning.The clustering structures can
be generated in two ways: choice of objects repre-
sentation or choice of clustering algorithms (Fred and
Jain, 2005). This approach is focused on the merg-
ing process of the clustering structures using a hy-
pergraph representation (Strehl and Ghosh, 2003), a
co-association matrix with the similarity measure be-
tween patterns (Fred and Jain, 2005) or a probabil-
ity distribution in the space of cluster labels (Topchy
et al., 2005).
3.1.4 Collaborative Clustering
The last approach, called collaborative clustering, has
different methods that collaborate together during a
refinement step of their results and share informa-
tion throughout the clustering process, to converge
towards a similar result until all the results have al-
most the same number of clusters, and all the clusters
are statistically similar. At the end of this process, as
the results have comparable structures, it is possible to
define a correspondence function between the clusters
and to apply a voting algorithm (Gancarski and Wem-
mert, 2007) (Forestier et al., 2008) (Forestier et al.,
2010).
3.2 Clustering Analysis applied to Sets
with the Same Media Type
The clustering methods have been so far applied to
sets with the same media type, such as text, image,
audio and video.
3.2.1 Text Clustering
The text clustering tries to find documents with many
words in common, grouping these documents into
the same cluster. Feature vector is the most widely
used data structure for text representation; each doc-
ument is a vector in a d-dimensional space, where
d is the number of features in the entire document
set and the vector entries represent the importance
or weight given to each feature in a specific doc-
ument (Meneses, 2006). There are different tech-
niques, called weighting models, to calculate the fea-
tures weight in text documents. Some techniques are
boolean weighting, frequency weighting, TF x IDF
weighting and TFC weighting. The most used is the
standard function TF-IDF (Term Frequency Inverse
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
136

Document Frequency) (Sebastiani, 2002). TF is the
frequency of the feature in a document and IDF is the
inverse frequency of the feature in all documents:
id f ( f
l
) = log
n
d f ( f
l
)
, (1)
where f
l
is the lth feature, n is the total number of
documents, and d f ( f
l
) is the number of documents
that contains the lth feature.
3.2.2 Image Clustering
The image clustering tries to find an image mapping
into clusters, such that images in the same cluster
have essentially the same information. The images
are commonly represented in feature vectors, graphs
and trees. The visual features of an image can be clas-
sified in several types, such as color, texture and logi-
cal (Choubassi et al., 2007). The first type, color fea-
tures, is used to describe the color distribution of the
image constructing a frequency histogram in several
color spaces such as RBG, YUV and HSV. The sec-
ond type, texture features, tries to find visual patterns
in images searching homogeneous regions. Some tex-
ture analysis techniques are energy, entropy, inverse
difference moment, inertia and correlation. The last
type, logical features, contains information about ob-
jects into images and their spatial relationships. Some
of these features are curvature, shape, interest points
and region positions.
3.2.3 Audio Clustering
The audio clustering tries to identify and group to-
gether all speech segments that were produced by the
same speaker, background conditions or channel con-
ditions (Lu et al., 2002) (Meinedo and Neto, 2003).
The audio sources can be analyzed in three layers:
acoustic characteristics, audio signatures and seman-
tic models (Liu et al., 1998). The acoustic character-
istics layer analyzes low level generic features such as
loudness, pitch period and bandwidth of an audio sig-
nal. The audio signature layer is an intermediate-level
associated with different sounding objects. The se-
mantic models layer is a high level analysis that uses
some prior known semantic rules about the structure
of audio in different scene types. In the clustering
process, the audio features can be extracted in short-
term frame level and long-term clip level (Wang et al.,
2000). A frame is defined as a group of neighboring
samples with a stationary audio signal and short-term
features such as volume and Fourier transform coef-
ficients can be extracted. A clip is defined as a se-
quence of frames and clip-level features usually char-
acterizing how frame-level features change over a clip
(Wang et al., 2000). Some clip level features are vol-
ume based, ZCR based, pitch based, frequency based,
etc.
3.2.4 Video Clustering
The video clustering has a challenge to simultane-
ously handle multimode videos with three elements:
images, audio and motion (Hoi and Lyu, 2008). In
the process of grouping video, the features are ex-
tracted from shots or frames (Zhong and Hongjiang,
1997). The shots capture continuous action in an un-
interrupted segment of video frame sequences, with
or without movement, so one shot is composed of one
or more frames (Ngo et al., 2001) (Yeung et al., 1996).
The features extracted from the shots are related to
temporal aspects such as variance and movement,
while the frames are drawn from issues related to
static images such as color and texture. The most dis-
cernible difference between static images and video
sequences comes from the movement and changes
(Dimitrova and Golshani, 1995). However, most at-
tempts of processing video do not analyze the move-
ment for its difficult handling.
4 AN ENSEMBLE APPROACH
FOR CMO CLUSTERING
Cluster analysis applied to a CMO set has a special
restriction: the method must analyze the multiple me-
dia types present in this kind of objects. In the re-
viewed literature, the combination of multiple cluster-
ing structures can be used when the sets are too com-
plex to give a unique clustering structure. Within such
approaches, the clustering ensemble is used when
the different clustering structures are independent and
complementary. Considering that media types present
in CMOs have independent and complementary infor-
mation, this research proposes an ensemble of cluster-
ing structures generated from several media types, is-
suing the following research question: Will a cluster-
ing ensemble be able to find an underlying structure
in a mix of several media types present in CMOs?
A clustering ensemble for CMOs permits a stan-
dalone exploration of the different media types
present in this kind of objects. In this way, the pro-
posed ensemble can take advantage of the research
advances in text, image, audio and video cluster-
ing.The proposed ensemble approach for CMO clus-
tering is presented in figure 2 with four kinds of com-
ponents: a separator, several clusterers, a mapper and
a combiner.
CLUSTERING COMPLEX MULTIMEDIA OBJECTS USING AN ENSEMBLE APPROACH
137

Figure 2: The proposed ensemble approach for clustering CMOs. The input is a CMO set and the output is a fuzzy matrix,
expressing that objects can belong to more than one cluster with different membership degrees.
The input is a CMO set X = {x
1
,x
2
,...,x
n
} and the
output is the final clustering structure, which is a n×k
fuzzy matrix u
ens
expressing that objects can belong
to more than one cluster with different membership
degrees, where n is the number of CMO in the set and
k is the number of clusters. The probability that ob-
ject x
i
belongs to cluster c
j
is given by u
ens
[i, j], where
0 ≤ u
ens
[i, j] ≤ 1. In the fuzzy matrix the rows repre-
sent objects (i) and the columns represent clusters ( j)
(Zhang and Rueda, 2005)(Carvalho, 2007).
The proposed ensemble has a specific restriction:
the clusterers must create clustering structures with
equal number of groups k. The ensemble approach is
described in the following subsections.
4.1 Separator of Media Types
In the literature review related with ensembles, the
clustering structures are generated in two ways:
choice of objects representation or choice of clus-
tering algorithms (Fred and Jain, 2005). The pro-
posed clustering ensemble creates the independent
structures evaluating different media types, so the
separator component preprocesses each CMO and
generates a dataset X
r
for each media type r in
{text, image,audio,video}. Those datasets are the en-
tries to the different clusterers and to the combinator
component.
4.2 Clusterers for each Media Type
The ensemble has several clusterers that produce a
clustering structure for a specific media type, where
each structure is a fuzzy matrix. Let u
text
be the fuzzy
matrix generated by a clustering method with the text
information of the CMO set. In the same way u
image
,
u
audio
and u
video
are generated. Each clustering struc-
ture must have the same number of groups k.
4.3 Mapper of the Clustering Structures
This component defines a correspondence function
between the k clusters in the different clustering struc-
tures. For each clustering structure u
r
, with r in
{text, image,audio,video}, a vector of labels λ
r
is de-
fined, which has the cluster with highest membership
value in u
r
for each object. In (Forestier et al., 2010),
the computation of a confusion matrix between each
pair of vector λ
r
is proposed for determining the clus-
ter mapping. The confusion or matching matrix M
p,q
between the two vectors of labels λ
p
and λ
q
is a k × k
matrix defined as:
M
p,q
=
α
p,q
1,1
... α
p,q
1,k
.
.
.
α
p,q
k,1
... α
p,q
k,k
(2)
The confusion matrix represents the intersection
α
p,q
j,h
between the cluster c
j
of the vector λ
p
and the
cluster c
h
of the vector λ
q
:
α
p,q
j,h
=
c
j
T
c
h
c
j
(3)
A cluster c
j
is the corresponding cluster of c
h
if
it is the most similar to c
h
. The similarity is com-
puted observing the intersection α
p,q
j,h
and the distribu-
tion ρ
p,q
j
of the cluster c
j
in all the clusters of λ
q
:
ρ
p,q
j
=
k
∑
t=1
(α
p,q
j,t
)
2
(4)
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
138

Finally, the adequacy ω
p,q
j,h
of a cluster c
j
to a clus-
ter c
h
is:
ω
p,q
j,h
= ρ
p,q
j
× α
p,q
j,h
(5)
Thus, the corresponding cluster of c
j
in the vec-
tor of labels λ
q
is the cluster c
h
that maximizes the
adequacy ω
p,q
j,h
. If there is a conflict between the cor-
responding clusters, the adequacy ω
p,q
j,h
will resolve
it by finding the next maximum. The output of the
mapper component is the clustering structures u
r
or-
ganized according to their corresponding clusters.
4.4 Combiner of the Clustering
Structures
This component has a challenge: the clustering struc-
tures can have different amounts of data because some
CMO could be incomplete. The proposed strategy is
a voting function with two weights that represent the
clustering structure quality and the size of the data
space evaluated for each media type. The first weight,
the clustering structure quality Q
r
of the media type r
in {text,image, audio, video}, is the value of an inter-
nal validity index for the clustering structure u
r
. This
weight is computed with the Xie-Beni index, which
is the combination of compactness in the same cluster
and separateness in different clusters:
Q
r
=
∑
k
j=1
∑
n
i=1
(u
r
[i, j])
2
kx
i
− v
j
k
2
n · min
i j
kv
i
− v
j
k
2
(6)
where v
j
is the center of cluster c
j
(Xie and Beni,
1991). The second weight, S
r,i
, is computed for each
media type r of each object x
i
. It represents the size of
the data space evaluated for each media type r of the
object x
i
as the ratio between the amount of non-zero
values in the feature vector of the media type r and
the size of the complete object x
i
:
S
r,i
=
|
non zero(x
r,i
)
|
|
x
i
|
(7)
Finally, the proposed voting function is a weighted
average of the u
r
fuzzy matrices:
u
ens
[i, j] =
1
R
∑
r
((Q
r
× S
r,i
)u
r
[i, j]) (8)
where R = 4 is the number of fuzzy matrices and
r in {text,image,audio, video}. The u
ens
[i, j] values
represent the membership degree of the CMO repre-
sented by x
i
to the cluster c
j
. The u
ens
[i, j] values cre-
ate the output of the ensemble that is a u
ens
matrix.
5 EVALUATION
Sets with large amounts of CMOs arise in some appli-
cations, like webpage search engines, which index a
large number of documents for information retrieval
(Wong and Fu, 2000). Most of the webpage search
engines divide the indexed documents into a number
of classes. Due to the massive increase in the amount
of web pages, the indexing must be developed by au-
tomatic systems through clustering analysis (Wong
and Fu, 2000). Considering that a webpage is a CMO
in itself, the proposed clustering ensemble is tested in
a webpage set.
The goal of the evaluation is to determine which
clustering approach creates structures closer to the
true classification. The organization of this section is
the following: the first subsection describes the clus-
tering prototypes developed for the ensemble; the sec-
ond subsection presents the experiment designs, and
the last subsection presents results and a discussion
about them.
5.1 Clustering Prototypes
For evaluating the proposed clustering ensemble in a
CMO set, it is necessary to develop at least two clus-
tering prototypes of different media types. In this pa-
per are developed a text clustering prototype and an
image clustering prototype.
The first prototype is developed with the text in-
formation extracted from the web pages and they are
represented in feature vectors weighted with the TF x
IDF function. The feature vectors for text representa-
tion have two specific problems: they are high dimen-
sional and they possess a sparse condition (Dhillon
and Modha, 2001) (Liu et al., 2003) (Feng et al.,
2010). The vectors are high dimensional because they
have been formed by a large number of features of
the entire document set. Additionally, the vectors are
very sparse because they contain few features of the
total number of them in the entire document set, so
the vectors have only a small number of non-zero or
significant values.
For high dimensional and sparse vectors problems
some authors recommend the application of a kernel
method (Hashimoto et al., 2009), which formulates
learning in a reproduction of the Hilbert space H of
functions defined on the data domain, expanded in
terms of a kernel trick. With a kernel trick, the ob-
jects to be clustered are mapped to a high dimensional
feature space, computing a linear partition in the new
space (Filippone et al., 2008). In applications where
the dimensionality of each x
i
exceeds n, a learning
problem is computationally inefficient, particularly if
CLUSTERING COMPLEX MULTIMEDIA OBJECTS USING AN ENSEMBLE APPROACH
139

objects are mapped into a Hilbert space (Hofmann
et al., 2008). However, with the kernel trick, a set of
nonlinearly separable objects can be transformed into
a higher feature space dimension with the possibility
to be linearly separable without knowledge about the
mapping function (Xu and Wunsch, 2005).
So, the text clustering prototype is developed with
a method called KFCM (kernel fuzzy c-means) (Yang
et al., 2007), where the feature vectors are mapped
into a high dimensional space by selecting a kernel
function.Then they are separated into some clusters
by the fuzzy c-means clustering algorithm.
The second prototype, image clustering, is devel-
oped with color features and with the text information
related to the images. The feature vector that rep-
resents the webpage x
i
is constructed in two stages.
First, the content of each image is downloaded and a
frequency histogram is computed in the RGB space.
Then, the histograms are averaged. In the second
stage, the text information related to the images is in-
dexed with the TF x IDF function. In order to fulfill
this purpose, the ”img” labels of the webpage are ex-
tracted. The final vector is a feature concatenation of
the two stages creating a high dimensional data; thus
the KFCM method is used to create the fuzzy clusters.
5.2 Experiment Design
For using the proposed ensemble in a CMO clustering
task, four tests are developed with different datasets.
The tests use a database of web pages from the open
directory project (http://www.dmoz.org/), which is
a human-edited directory of the web (Osinski and
Weiss, 2004).The tests were conducted varying the
number of webpages n in {30,50,90,480} for con-
trasting the following clustering approaches:
• The text clustering.
• The image clustering.
• The joint-feature vector clustering.
• The clustering ensemble with a voting function
that averages the results of the text and image
clustering.
• The proposed clustering ensemble with a voting
function that averages the results of the text and
image clustering using both weights: the cluster-
ing structure quality Q
r
and the size S
r,i
of the data
space evaluated for each media type.
For comparing the clustering quality, an external
index validation is calculated. In this paper, the
Hubert’s Γ statistic has been chosen as the index
validation, because it has detected the correct
number of clusters in several experiments (Hubert
and Arabie, 1985). Let C
∗
= {c
∗
1
,c
∗
2
,...,c
∗
k
} be a
clustering structure obtained for an object set X, let
C = {c
1
,c
2
,...,c
k
} be the real clustering structure of
the object set and let Z and Y be the matrices that
represent such structures:
Z(i, j) = {1, if x
i
and x
j
belong to the same cluster
in C
∗
, and 0 otherwise},∀i, j = 1...n
Y (i, j) = {1, if x
i
and x
j
belong to the same
cluster in C, and 0 otherwise},∀i, j = 1...n
Hubert’s statistic is defined as:
Γ(C
∗
,C) = (1/M)
n−1
∑
i=1
n
∑
j=i+1
Z(i, j)Y (i, j), (9)
where M is the maximum number of pairs in the ob-
ject set (M = n(n − 1)/2) and n is the total number of
objects in the X set. High values of this index indicate
a strong similarity between the real clusters C and the
obtained clusters C
∗
.
5.3 Results and Discussion
Table 1 summarizes the results for the four tests de-
scribed above showing Hubert’s statistic for the con-
trasted approaches.
The values presented in Table 1 show that the ob-
tained results from the image clustering approach are
not close to the true classification of the objects. They
also show that the performance of all the approaches
declines when the number of objects in the tests in-
crease, because the dimensionality of the feature vec-
tors increases too.
Figure 3 shows the mean values of the test results.
It can be seen in the figure that the weighted average
ensemble has a better performance than the average
ensemble, achieving a balance between the uneven
performance of the text clustering approach and the
image clustering approach.
An important finding is the contrast between
the joint feature vector clustering approach and the
weighted average ensemble approach. The proce-
dure of Fisher’s least significant difference (LSD) is
used to determine whether the means of these two ap-
proaches are significantly different. The LSD proce-
dure indicates that there is significant statistical dif-
ference between these approaches using a confidence
level of 95 percent. So, Hubert’s statistic indicates
that the proposed ensemble creates clustering struc-
tures more similiar to the real classification than a
joint feature vector for the evaluated sets.
An interesting discussion is related with the com-
putational complexity of the proposed ensemble,
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
140
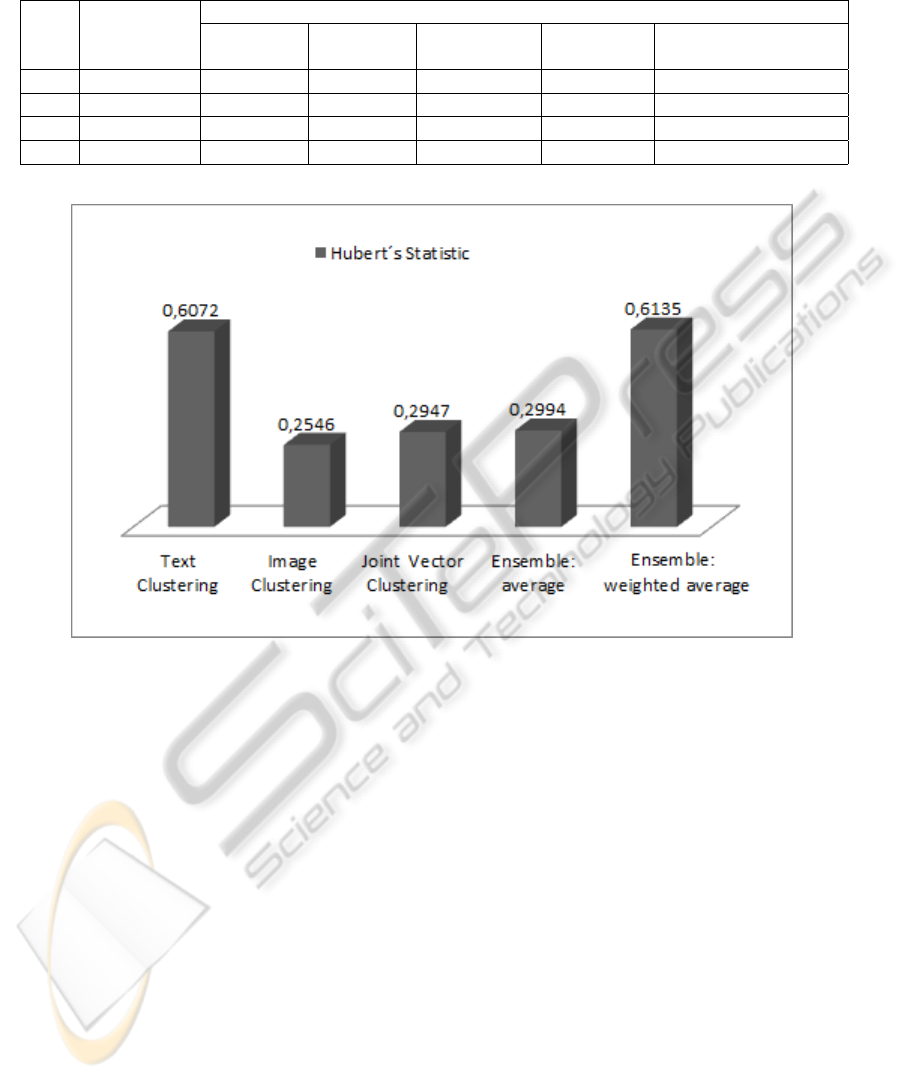
Table 1: Hubert’s statistic for the contrasted approaches. High values of this statistic indicate better results. The best values
are in bold font.
Contrasted Approaches
Test Number of Text Image Joint vector Ensemble: Proposed ensemble:
webpages clustering clustering clustering average weighted average
1 30 0,7793 0,4850 0,5595 0,5794 0,7908
2 50 0,7494 0,4736 0,5517 0,5583 0,7632
3 90 0,5436 0,0369 0,0478 0,0369 0,5436
4 480 0,3565 0,0230 0,0200 0,0230 0,3565
Figure 3: Mean values of Hubert’s statistic. There is significant statistical difference between the joint vector clustering and
the weighted average ensemble.
which remains to be cubic O(n
3
) in the mapper com-
ponent of the ensemble. This means that when the
number of clusters significantly increases, the diffi-
culty increases in a cubic order.
6 CONCLUSIONS
This paper addresses the clustering of complex mul-
timedia objects with a special restriction: the method
must analyze different media types. An ensemble was
proposed for this purpose, which generates a cluster-
ing structure for each media type of a CMO set. The
clustering structures generated must be reorganized
in a mapping process that defines a correspondence
function between the clusters of all the structures. Fi-
nally, a voting function with a weighted average of the
clustering structures generates a final result. The pro-
posal has a restriction: the ensemble does not consider
different numbers of groups in the clustering struc-
tures. A new component should be included in the
proposed ensemble for considering different numbers
of groups,but this is part of a future research.
The proposed ensemble was applied to cluster
webpages constructing a text clustering prototype and
an image clustering prototype.Hubert’s statistic was
used to evaluate the ensemble performance using four
datasets of web pages. Results showed that the pro-
posed ensemble creates clustering structures more
similar to the real classification than a joint feature
vector.
A cubic computational complexity is a disadvan-
tage of the ensamble due to the fact that, when the
number of groups increases, the complexity increases
in a cubic order, so this is an emergent research line.
Other future works are: to improve the clustering pro-
totypes, to create new clustering structures with other
resources, and to use larger and new datasets.
CLUSTERING COMPLEX MULTIMEDIA OBJECTS USING AN ENSEMBLE APPROACH
141

ACKNOWLEDGEMENTS
The authors would like to acknowledge support from
ARTICA (Alianza Regional para las TICs Aplicadas)
and the Cocreation project which is supported by Uni-
versidad de Antioquia, Universidad Nacional Sede
Medellin, Universidad Pontificia Bolivariana, Univer-
sidad EAFIT, Universidad de Medelln and UNE.
REFERENCES
Algergawy, A., Schallehn, E., and Saake, G. (2008). A
schema matching-based approach to xml schema clus-
tering. In Proceedings of the 10th International Con-
ference on Information Integration and Web-based
Applications & Services, pages 131–136, New York,
NY, USA. ACM.
Bae, E. and Bailey, J. (2006). Coala: A novel approach for
the extraction of an alternate clustering of high quality
and high dissimilarity. In IEEE International Confer-
ence on Data Mining, pages 53–62.
Caruana, R., Elhawary, M., Nguyen, N., and Smith, C.
(2006). Meta clustering. In Proceedings of the Sixth
International Conference on Data Mining, ICDM 06,
pages 107–118, Washington, DC, USA. IEEE Com-
puter Society.
Carvalho, F. (2007). Fuzzy c-means clustering methods for
symbolic interval data. Pattern Recognition Letters,
28(4):423–437.
Choubassi, M. E., Nefian, A., Kozintsev, I., Bouguet, J., and
Wu, Y. (2007). Web image clustering. In IEEE Inter-
national Conference on Acoustics, Speech and Signal
Processing, volume 4, pages 15–20.
Davidson, I. and Qi, Z. (2008). Finding alternative clus-
terings using constraints. In Proceedings of the 2008
Eighth IEEE International Conference on Data Min-
ing, pages 773–778, Washington, DC, USA. IEEE
Computer Society.
Dhillon, I. S. and Modha, D. S. (2001). Concept decom-
positions for large sparse text data using clustering.
Machine Learning, 42(1-2):143–175.
Dimitrova, N. and Golshani, F. (1995). Motion recovery
for video content classification. ACM Trans. Inf. Syst.,
13:408–439.
Dy, J. and Brodley, C. (2004). Feature selection for unsu-
pervised learning. Journal of Machine Learning Re-
search, 5:845–889.
Feng, Z., Bao, J., and Shen, J. (2010). Dynamic and adap-
tive self organizing maps applied to high dimensional
large scale text clustering. In Software Engineering
and Service Sciences ICSESS, pages 348–351. IEEE
International Conference.
Filippone, M., Camastra, F., Masulli, F., and Rovetta, S.
(2008). A survey of kernel and spectral methods for
clustering. Pattern Recognition, 41:176–190.
Forestier, G., Wemmert, C., and Gancarski, P. (2010). To-
wards conflict resolution in collaborative clustering.
In Intelligent Systems (IS), 2010 5th IEEE Interna-
tional Conference, pages 361–366.
Forestier, G., Wemmert, C., and Ganc¸arski, P. (2008). Mul-
tisource images analysis using collaborative cluster-
ing. EURASIP J. Adv. Signal Process, 2008:133:1–
133:11.
Francois, O., Ancelet, S., and Guillot, G. (2006). Bayesian
clustering using hidden markov random fields in spa-
tial population genetics. Genetics, 174:805–816.
Fred, A. and Jain, A. (2005). Combining multiple clus-
terings using evidence accumulation. IEEE Transac-
tions on Pattern Analysis and Machine Intelligence,
27(6):835–850.
Gancarski, P. and Wemmert, C. (2007). Collaborative multi-
step mono-level multi-strategy classification. Multi-
media Tools Appl., 35:1–27.
Halkidi, M., Batistakis, Y., and Vazirgiannis, M. (2002).
Cluster validity methods: part i. ACM SIGMOD
Record, 31(2).
Hashimoto, W., Nakamura, T., and Miyamoto, S. (2009).
Comparison and evaluation of different cluster valid-
ity measures including their kernelization. Journal of
Advanced Computational Intelligence, 13(3).
Hofmann, T., Scholkopf, B., and Smola, A. (2008). Kernel
methods in machine learning. The Annals of Statistcs,
36(3):1171–1220.
Hoi, S. and Lyu, M. (2008). A multimodal and multilevel
ranking scheme for large-scale video retrieval. Multi-
media, IEEE Transactions on, 10:607–619.
Hubert, L. and Arabie, P. (1985). Comparing partitions.
Journal of Classification, 2(1):193–218.
Hunter, J. and Choudhury, S. (2003). Implementing preser-
vation strategies for complex multimedia objects. In
Seventh European Conference on Research and Ad-
vanced Technology for Digital Libraries, ECDL 2003,
pages 473–486. Springer.
Jain, A., Murty, M., and Flynn, P. J. (1999). Data clustering:
a review. ACM Computing Surveys, 31(3):264–323.
Jain, A. K. (2010). Data clustering: 50 years beyond k-
means. Pattern Recognition Letters, 31(8):651–666.
Jiamthapthaksin, R., Eick, C. F., and Rinsurongkawong, V.
(2009). An architecture and algorithms for multi-run
clustering. In Computational Intelligence Symposium
on Data Mining CIDM 09, pages 306–313.
Kriegel, H.-P., Kunath, P., Pryakhin, A., and Schubert,
M. (2008). Distribution-based similarity for multi-
represented multimedia objects. In Proceedings of the
14th international conference on Advances in multi-
media modeling, MMM 08, pages 155–164, Berlin,
Heidelberg. Springer-Verlag.
Law, M. H. C., Topchy, A. P., and Jain, A. K. (2004). Mul-
tiobjective data clustering. In Proceedings of the 2004
IEEE computer society conference on Computer vi-
sion and pattern recognition, CVPR 04, pages 424–
430, Washington, DC, USA. IEEE Computer Society.
Liu, T., Liu, S., Chen, Z., and Ma, W. (2003). An evaluation
on feature selection for text clustering. In Proceed-
ings of the 20th International Conference on Machine
Learning, pages 448–495. AAAI Press.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
142

Liu, Z., Wang, Y., and Chen, T. (1998). Audio feature ex-
traction and analysis for scene segmentation and clas-
sification. In Journal of VLSI Signal Processing Sys-
tem, volume 20, pages 61–79.
Lu, L., Zhang, H.-J., Member, S., and Jiang, H. (2002).
Content analysis for audio classification and segmen-
tation. IEEE Transactions on Speech and Audio Pro-
cessing, 10(4):504–516.
Meinedo, H. and Neto, J. (2003). Audio segmentation, clas-
sification and clustering in a broadcast news task. In
Acoustics, Speech, and Signal Processing, 2003. Pro-
ceedings. (ICASSP ’03).
Meneses, E. (2006). Vectors and graphs: Two represen-
tations to cluster web sites using hyperstructure. In
Latin American Web Congress, pages 20–25.
Ngo, C.-W., Pong, T.-C., and Zhang, H.-J. (2001). On clus-
tering and retrieval of video shots. In Proceedings of
the ninth ACM international conference on Multime-
dia, MULTIMEDIA 01, pages 51–60, New York, NY,
USA. ACM.
Osinski, S. and Weiss, D. (2004). Conceptual clustering
using lingo algorithm: Evaluation on open directory
project data. In IIPWM04, pages 369–377.
Romesburg, C. (2004). Cluster Analysis for Researchers.
Lulu Press.
Sebastiani, F. (2002). Machine learning in automated text
categorization. ACM Computing Surveys, 34(1):1–47.
Strehl, A. and Ghosh, J. (2003). Cluster ensembles — a
knowledge reuse framework for combining multiple
partitions. J. Mach. Learn. Res., 3:583–617.
Topchy, A., Jain, A. K., and Punch, W. (2005). Clustering
ensembles: Models of consensus and weak partitions.
IEEE Transactions on pattern analysis and machine
intelligence, 27:1866–1881.
Wang, Y., Liu, Z., and Huang, J.-C. (2000). Multime-
dia content analysis using both audio and visual cues.
IEEE Signal Processing Magazine, 17(6):12–36.
Wong, W. and Fu, A. (2000). Incremental document clus-
tering for web page classification. In In IEEE 2000
Int. Conf. on Info. Society in the 21st, pages 5–8.
Xie, X. and Beni, G. (1991). A validity measure for fuzzy
clustering. IEEE Trans. on Pattern Analysis and Ma-
chine Intelligence, 13(4):841–846.
Xu, R. and Wunsch, D. (2005). Survey of clustering algo-
rithms. IEEE Trans. Neural Networks, 16(3):645–667.
Yang, A., Jiang, L., and Zhou, Y. (2007). A kfcm-based
fuzzy classifier. In Proceedings of the Fourth Interna-
tional Conference on Fuzzy Systems and Knowledge
Discovery - Volume 02, FSKD 07, pages 80–84, Wash-
ington, DC, USA. IEEE Computer Society.
Yang, Y., Zhuang, Y.-T., Wu, F., and Pan, Y.-H. (2008). Har-
monizing hierarchical manifolds for multimedia doc-
ument semantics understanding and cross-media re-
trieval. IEEE Transactions on Multimedia, 10(3):437–
446.
Yeung, M., Yeo, B., and Liu, B. (1996). Extracting story
units from long programs for video browsing and nav-
igation. In Proceedings of the 1996 International Con-
ference on Multimedia Computing and Systems, pages
296–305, Washington, DC, USA. IEEE Computer So-
ciety.
Zhang, Y. and Rueda, L. (2005). A geometric framework to
visualize fuzzy-clustered data. In Chilean Computer
Science Society, SCCC.
Zhong, D. and Hongjiang, D. Z. (1997). Clustering methods
for video browsing and annotation. Technical report,
In SPIE Conference on Storage and Retrieval for Im-
age and Video Databases.
Zhuang, Y., Yi, Y., and Fei, W. (2008). Mining seman-
tic correlation of heterogeneous multimedia data for
cross- media retrieval. IEEE Transactions on Multi-
media, 10(2):221–229.
CLUSTERING COMPLEX MULTIMEDIA OBJECTS USING AN ENSEMBLE APPROACH
143
