COMBINATIONS OF OPTION SPREADS
Dmytro Matsypura and Vadim G. Timkovsky
The University of Sydney Business School, Sidney, NSW, Australia
Keywords:
Arbitrage, Box, Hedging, High-frequency, Leg, Margin, Offset, Option, Portfolio, Risk, Spread, Trading.
Abstract:
Having been constructed as trading strategies, option spreads are also used in margin calculations for offsetting
positions in options. All option spreads that appear in trading and margining practice have two, three or four
legs. It is well-known that the option spreads with three and four legs are combinations of two option spreads
with two legs, and that hedging mechanisms of these combinations consolidate hedging mechanisms of their
components. Although more complex combinations with similar properties can be traced in regulatory litera-
ture of 2003, they have not yet been studied and used. In this paper we develop a theory for the construction
of multi-leg option spreads as combinations of well-known option spreads with two, three and four legs. We
show how multi-leg option spreads with extreme properties can maximize arbitrage opportunities in trading
options and substantially reduce margin requirements for option portfolios.
1 INTRODUCTION
Option spreads with two, three and four legs such as
bull and bear spreads, butterfly, condor, iron butter-
fly, iron condor and box spreads have been known for
more than three decades and have become standard in
options trading; cf. (McMillan, 2002; Cohen, 2005;
Curley, 2008). Descriptions of more complex spreads
appeared as efficient means of margin reductions in
2003. It is important to explain how these spreads
were motivated.
1.1 Regulatory Breakthrough
By the end of the nineties, it was commonly recog-
nized that margin regulations impose excessively high
minimum margin requirements, especially for option
portfolios. This can be partially explained by the fact
that option spreads permitted for offsetting by mar-
gin regulations by that time had at most four legs.
1
However, it is well-known that the more legs an op-
tion spread has the more margin reduction it gives.
As shown in (Matsypura and Timkovsky, 2011), just
one additional leg can save several thousand dollars
on margin. Thus, the reduction of minimum margin
requirements can be achievedby constructing new op-
tion spreads with a larger number of legs.
1
A leg of an option spread or offset based on this spread
is a position in options with the same exercise price and
expiry date.
Option spreads with up to 12 legs appeared as
combinations of option spreads with two, three and
four legs in August 2003 when the CBOE
2
proposed
new margin rules based on these combinations that
were called complex spreads (CBOE, 2003). After
two revisions of this proposal (CBOE, 2004; CBOE,
2005), the SEC
3
approved these rules (SEC, 2005)
and added them to NYSE Rule 431 in December
2005. In August 2007, these rules were also recog-
nized in Canada (IDA, 2007).
1.2 Motivation
The regulatory breakthrough of 2005, however, re-
ceived a limited response of the brokerage industry by
the following two reasons: firstly, the definition of the
complex spreads was given in a text form that does
not allow for complete understanding of their struc-
ture, and hence how these spreads can be utilized;
secondly, the interest to multi-leg option spreads had
been lost because the risk-based margining methodol-
ogy that had become popular in the U.S. in 2005 of-
fered computationally easier solutions. Consequently,
option spreads with more than four legs are still not
being used, primarily because they have neither been
studied nor properly understood.
Multi-leg option spreads thus call for academic re-
search that shall explain how they can be constructed,
2
The Chicago Board Options Exchange.
3
The U.S. Securities and Exchange Commission.
321
Matsypura D. and G. Timkovsky V..
COMBINATIONS OF OPTION SPREADS.
DOI: 10.5220/0003798003210331
In Proceedings of the 1st International Conference on Operations Research and Enterprise Systems (ICORES-2012), pages 321-331
ISBN: 978-989-8425-97-3
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

what advantage they give, and how they can be uti-
lized in options trading and marginingpractice. To the
best of our knowledge, this kind of research has never
been attempted. As we show in this paper, 12 legs is
not the final step. We discover new multi-leg option
spreads that have the same hedging mechanism as that
of complex option spreads and propose a full charac-
terization of option spreads with any number of legs.
We also formulate integer programs that demonstrate
that multi-leg option spreads maximize arbitrage op-
portunities in options trading and substantially reduce
margin requirements in margin accounts with options.
2 MAIN SPREADS
A vector model of option spreads with up to four legs
was proposed in (Matsypura and Timkovsky, 2011).
In this section we give an extension of this model that
deals with option spreads of different width.
2.1 Vector Model of Option Spreads
Let d ≥ 2 be a positive integer. Option spreads of
dimension d are integer vectors
v = ( c
1
c
2
··· c
d
p
1
p
2
··· p
d
)
whose components are associated with positions in
options in a margin account as follows.
The component c
j
, 1 ≤ j ≤ d, is the number of
option contracts in the jth call option series, with the
exercise price e
j
. Similarly, the component p
j
is the
number of option contracts in the jth put option se-
ries, with the same exercise price e
j
.
Nonzero components represent legs. A positive,
negative or zero component means that it is a long,
short leg or a leg is absent, respectively. A zero
spread, denoted 0, is a spread without legs.
Let a be a nonnegativeinteger. Then av is a multi-
ple of v with factor a. A spread is said to be prime if
it is not a multiple of another spread with factor more
than one. Thus, 0 is a prime spread. If v is a prime
spread, then a is a multiplicity of av. If not stated
otherwise, we assume further only prime spreads.
Treating spreads as vectors we can add and sub-
tract them, multiply by an integer scalar, cyclicly shift
their components and take their transpositions, i.e.,
create the spreads ¯v, where the components c
i
and p
i
are transposed for all i = 1,2, . . . , d.
We assume that the exercise prices are all different
and placed in increasing order,i.e., e
1
< e
2
< ··· < e
d
.
The set {e
1
,e
2
,...,e
d
} is called an exercise domain.
If the exercise prices are separated by the same price
interval, then the length of the interval, D, is the ex-
ercise differential of the domain, and the exercise do-
main is said to be uniform.
4
In what follows, we consider only uniform exer-
cise domains and option spreads on the same exercise
domain. Therefore, it will be convenient to normal-
ize all prices and costs by divisor D. Thus, we will
further assume that all exercise prices and all option
prices have been normalized, and hence all exercise
domains have exercise differential 1.
Definition 1. Let w and k be positive integers such
that w < d and k ≤ 2d, and let v
1
,v
2
,...,v
k
be the
sequence of leg indices in a spread v of dimension d
such that
e
v
1
≤ e
v
2
≤ ··· ≤ e
v
k
If e
v
j+1
−e
v
j
= 0 or w for each j = 1,2,...,k−1, then
v is a uniform spread of width w.
We consider only uniform spreads because only
they are being used in practice. Besides, as we con-
sider only normalized prices, the width of spreads will
always be integer in the set {1,2,...,d −1}. Simplest
uniform spreads are basic spreads. They can be de-
fined as follows:
Definition 2. A basic spread is uniform and has two
legs, 1 and −1, such that both legs are on the same
side, call or put. A basic spread is a basic call/put
spread if all its legs are on the call/put side. A basic
spread is a basic bull spread if its first leg is long;
otherwise it is a basic bear spread.
The first 12, 8, 4 spreads in Tables 1, 2, 3, present
all basic spreads of width 1, 2, 3 and dimension 4,
respectively. The abbreviations “dr” and “cr” mark
debit spreads and credit spreads.
5
Definition 3. All basic spreads are two-leg main
spreads. Let u and v, where u 6= −v, be a basic
bull spread and a basic bear spread, respectively, of
the same width w, and let u+ v be a uniform spread
of width w. Then u + v is a three- or four-leg main
spread of width w.
Although our attention will be focused on the case
of dimension four, all further results are valid for
any dimension higher than four. The set of all main
spreads of width 1, 2, 3 and dimension 4 is presented
in Tables 1, 2, 3, respectively. Note that butterfly and
4
Exercise prices of listed options of the same expiration
date generate a uniform exercise domain. For example, ac-
cording to http://finance.google.com, as of 02-AUG-2011,
5:50PM, exercise prices of options on the IBM stock listed
in NYSE and expiring on 20-AUG-2011 generated the uni-
form exercise domain {85,90,. .. , 270} of dimension 38.
5
The term debit/credit indicates that the spread is a re-
sult of a net debit/credit transaction, respectively.
ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems
322

Table 1: Main spreads of width 1 and dimension 4.
spread spread name calls puts legs net
a 1st bull call 1 -1 2 dr
b 2nd bull call 1 -1 2 dr
c 3rd bull call 1 -1 2 dr
e 1st bull put 1 -1 2 cr
f 2nd bull put 1 -1 2 cr
g 3rd bull put 1 -1 2 cr
-a 1st bear call -1 1 2 cr
-b 2nd bear call -1 1 2 cr
-c 3rd bear call -1 1 2 cr
-e 1st bear put -1 1 2 dr
-f 2nd bear put -1 1 2 dr
-g 3rd bear put -1 1 2 dr
a− b 1st long call butterfly 1 -2 1 3 dr
b− a 1st short call butterfly -1 2 -1 3 cr
b− c 2nd long call butterfly 1 -2 1 3 dr
c− b 2nd short call butterfly -1 2 -1 3 cr
e− f 1st long put butterfly 1 -2 1 3 cr
f− e 1st short put butterfly -1 2 -1 3 dr
f− g 2nd long put butterfly 1 -2 1 3 cr
g− f 2nd short put butterfly -1 2 -1 3 dr
a− c long call condor 1 -1 -1 1 4 dr
c− a short call condor -1 1 1 -1 4 cr
e− g long put condor 1 -1 -1 1 4 dr
g− e short put condor -1 1 1 -1 4 cr
a− e 1st long box 1 -1 -1 1 4 dr
e− a 1st short box -1 1 1 -1 4 cr
b− f 2nd long box 1 -1 -1 1 4 dr
f− b 2nd short box -1 1 1 -1 4 cr
c− g 3rd long box 1 -1 -1 1 4 dr
g− c 3rd short box -1 1 1 -1 4 cr
a− f 1st long call iron butterfly 1 -1 -1 1 4 dr
f− a 1st short call iron butterfly -1 1 1 -1 4 cr
b− g 2nd long call iron butterfly 1 -1 -1 1 4 dr
g− b 2nd short call iron butterfly -1 1 1 -1 4 cr
e− b 1st long put iron butterfly -1 1 1 -1 4 cr
b− e 1st short put iron butterfly 1 -1 -1 1 4 dr
f− c 2nd long put iron butterfly -1 1 1 -1 4 cr
c− f 2nd short put iron butterfly 1 -1 -1 1 4 dr
e− c long put iron condor -1 1 1 -1 4 cr
c− e short put iron condor 1 -1 -1 1 4 dr
a− g long call iron condor 1 -1 -1 1 4 dr
g− a short call iron condor -1 1 1 -1 4 cr
condor spreads, iron butterfly and iron condor spreads
of width 2 or 3 and dimension 4 do not exist.
Theorem 1. The number of main spreads of width w
and dimension d is n(w,d) =
6(d − w) + 8max{0,d − 2w} + 8max{0,d − 3w}.
Proof A direct count shows that for fixed w and
d the numbers of bull, bear or box spreads, but-
terfly or iron butterfly spreads, and condor or iron
condor spreads are 2(d − w), 4max{0,d − 2w}, and
4max{0, d − 3w}, respectively.
2.2 Portfolios and Linear Combinations
of Main Spreads
Let A denote the 2d × n matrix, where
n =
d−1
∑
w=1
n(w,d)
whose columns are all main spreads of dimension d.
If A(w, d) is the matrix of main spreads of width w
and dimension d, then
COMBINATIONS OF OPTION SPREADS
323

Table 2: Main spreads of width 2 and dimension 4.
spread spread name calls puts legs net
a 1st bull call 1 -1 2 dr
b 2nd bull call 1 -1 2 dr
e 1st bull put 1 -1 2 cr
f 2nd bull put 1 -1 2 cr
-a 1st bear call -1 1 2 cr
-b 2nd bear call -1 1 2 cr
-e 1st bear put -1 1 2 dr
-f 2nd bear put -1 1 2 dr
a− e 1st long box 1 -1 -1 1 4 dr
e− a 1st short box -1 1 1 1 4 cr
b− f 2nd long box 1 -1 -1 1 4 dr
f− b 2nd short box -1 1 1 -1 4 cr
Table 3: Main spreads of width 3 and dimension 4.
spread spread name calls puts legs net
a 1st bull call 1 -1 2 dr
e 1st bull put 1 -1 2 cr
-a 1st bear call -1 1 2 cr
-e 1st bear put -1 1 2 dr
a− e 1st long box 1 -1 -1 1 4 dr
e− a 1st short box -1 1 1 -1 4 cr
A = [ A(1,d) A(2,d) ··· A(d − 1, d) ]
In what follows, an integer column vector of size n
with nonnegative components will be associated with
the portfolio of main spreads taken in quantities equal
to the components of this vector. Such vectors consti-
tute a portfolio space.
An integer column vector of size 2d will be asso-
ciated with a spread, as we described in Section 2.1.
Such vectors constitute a spread space. Further, all
vectors in the portfolio/spread space will be denoted
by italic/direct bold letters.
Thus, the matrix A, as a left multiplier, transforms
portfolios of main spreads into linear combinations of
main spreads. As we show in Section 5, a portfolio of
main spreads can have multiple representations in the
form of linear combination of main spreads.
According to this assumptions, a main spread can
be presented in the following two forms:
• as a column vector of size n whose ith component
is 1 and the other components are 0s, that is de-
noted by e
i
(a presentation in the portfolio space);
the index i will be dropped if the main spread is
not specific; or
• as a column of A, i.e., as a column vector of size
2d, that is denoted by b
i
, if the main spread is the
ith column of A, or by b if the main spread is not
specific (a presentation in the spread space).
These forms are obviously related by the equation
Ae
i
= b
i
2.3 Market Risk of Main Spreads
It is well known that debit spreads are free of mar-
ket risk, i.e., they have no loss associated with un-
derlying instrument price changes, cf. (Cohen, 2005)
or (McMillan, 2002) for a detailed discussion. Credit
spreads, in contrast, are not free of market risk.
The maximum loss on a prime credit spread asso-
ciated with underlying instrument price changes is its
width in all cases except for a short call iron butterfly
and a short call iron condor for which the maximum
loss is two widths. Therefore, the market risk of a
main spread b is the integer
m(b) =













0 if b is a debit spread,
2w if b is
a short call iron butterfly
or short call iron condor
spread,
w otherwise.
(1)
In this paper, we consider the market risk of a main
spread to be its maintenance margin requirement.
Moreover, we consider only maintenance margin
requirements. Details related to a justification of the
market risk as a measure of maintenance margin re-
quirements and discussions on the relationship be-
tween maintenance and initial margin requirements
for main spreads can be found in (Matsypura and
Timkovsky, 2011). In what follows, the term “mar-
gin” will stand for a maintenance margin requirement.
ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems
324

3 COMPLEX SPREADS
The regulatory amendment of December 14, 2005,
initiated by the CBOE, was motivated by the obser-
vation that some combinations of main spreads have
the same risk profile as single main spreads. This can
be explained by the fact that the summation of main
spreads in such a combination turns out to be also a
main spread that is a resulting spread. These combi-
nations were named complex spreads. The margin of
a complex spread is exactly the margin of its resulting
spread (CBOE, 2003).
3.1 Table of Complex Spreads
Ten of the complex spreads are presented in Ta-
ble 4. The other ten are their transpositions, where the
names of the components have the words “call” and
“put” interchanged. Negations of these 20 produce
another 20, where the names of the components have
the words “long” and “short” interchanged. Thus, Ta-
ble 4 defines a total of 40 complex spreads. As com-
plex spreads 1 and 2, 4 and 5, 7 and 8 are isomorphic,
there exist only seven types of the complex spreads.
6
Note that there are no complex spreads of width
more than 1 and dimension 4 because otherwise they
would involve as components butterfly spreads of
width more than 1, which do not exist.
3.2 Advantage of Complex Spreads
The margins of complex spreads are exactly the mar-
gins of their resulting spreads, cf. (CBOE, 2003); and
a complex spread is an offset if its margin is less than
the total margin of its components. Hence, not all
complex spreads are offsets.
For example, the complex spread 6 in Table 4 has
three components: the 1st long call butterfly spreads
b− c, the 2nd long call butterfly spread a− b and the
3rd bull call spread c. All the three are debit spreads.
By formula (1), the market risks for these spreads are
zeros. The resulting spread is the 1st bull call spread
6
The regulatory definitions given in SEC Release 34-
52738, the CBOE Regulatory Circular and NYSE Rule 431
imply only these seven types. The CBOE gave some of
complex spreads the same names as those of their result-
ing main spreads. To avoid confusions, we do not use these
names. We should also emphasize that this paper presents
our mathematical interpretation of CBOE’s informal defini-
tions of complex spreads in a text form. Our goal was to
follow the idea given in the definitions as close as possible
and, at the same time, avoid inconsistencies that we found
in them. Any omission that someone may find in our math-
ematical interpretation of CBOE’s complex spreads will be
our responsibility.
a, which is also a debit spread. Therefore, the mar-
gin of the complex spread 6 is also zero. Thus, it is
not an offset, and there is no advantage of using it
for margin reductions. It is not hard to verify that all
complex spreads in Table 4 are not offsets. However,
their negations are offsets.
For example, since the bear call spread −a is a
credit spread, the margin of the negation of the com-
plex spread 6 is w, while the total margin of b− a,
c− b and −c, which are all credit spreads, is 3w.
Thus, the negation of the complex spread 6 is an offset
with advantage 2w.
In general, if a complex spread with the resulting
debit or credit spread is an offset, then it reduces the
total margin of its components by kw or (k− 1)w, re-
spectively, where k is the number of credit compo-
nents. Thus, the negations of the complex spreads 1
through 5, 6 through 9 and 10 reduce the margin by
w, 2w and 3w, respectively.
4 BEYOND COMPLEX SPREADS
Complex spreads are constructed as summations of
bull/bear spreads, long/short butterfly spreads and
long/short box spreads; cf. Table 4.
Developing the idea of complex spreads, we give
in this section definitions of other multi-leg spreads as
more general combinations of main spreads that we
call centipedes and millipedes.
7
4.1 Centipedes
Definition 4. A centipede is a set of main spreads
such that their linear combination with nonegative
integer coefficients is a nonzero multiple of a main
spread, which is the resulting spread of the centipede.
A nonzero multiple of a main spread, obviously,
generates a trivial centipede by itself. The margin rule
for complexspreads we formulated in the preamble of
Section 3 naturally applies to centipedes because they
have the same risk profiles as their resulting spreads.
Let a be a positive integer, 0 be a zero vector of
size n, and let b be a main spread. Then centipedes
7
Centipedes, as all other creatures, have even number of
legs (one pair of legs per body segment), and this number
can reach 200 and more. Centipedes usually do not bite hu-
mans but a few species, when provoked, can bite inflicting
painful wounds. Millipedes are creatures with number of
legs multiple of four (two pairs of legs per body segment).
Some species have over 400 legs. Millipedes are not preda-
tors as centipedes. – Wikipedia (terrestrial animals). It can
be observed that multi-leg spreads introduced in this section
have similar properties.
COMBINATIONS OF OPTION SPREADS
325

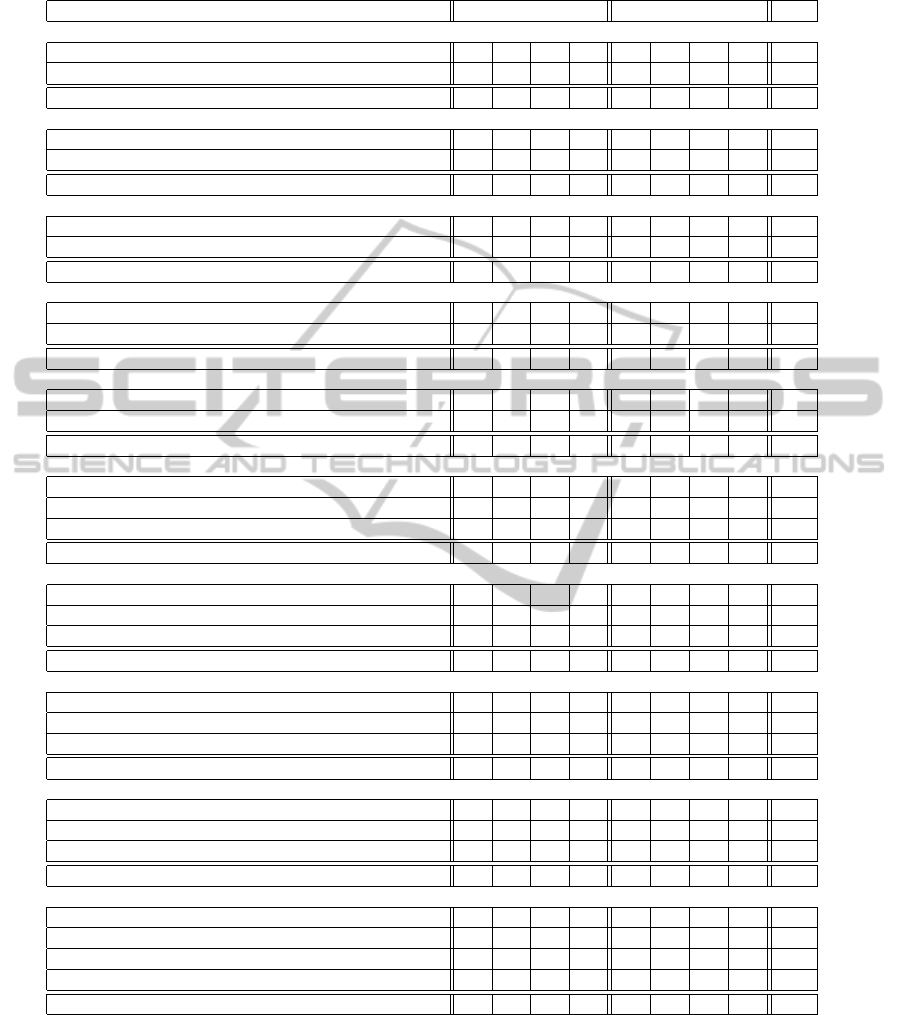
Table 4: CBOE’s complex spreads, their components and resulting spreads.
complex spread: component sum = resulting spread calls puts net
1. b+ (a− b) = a : 5 legs
2nd bull call 1 -1 dr
+ 1st long call butterfly 1 -2 1 dr
= 1st bull call 1 -1 dr
2. c+ (b− c) = b : 5 legs
3nd bull call 1 -1 dr
+ 2st long call butterfly 1 -2 1 dr
= 2nd bull call 1 -1 dr
3. (b− c) + (a− b) = a− c : 6 legs
2nd long call butterfly 1 -2 1 dr
+ 1st long call butterfly 1 -2 1 dr
= long call condor 1 -1 -1 1 dr
4. (a− b) + (e− a) = e− b : 7 legs
1st long call butterfly 1 -2 1 dr
+ 1st short box -1 1 1 -1 cr
= 1st long put iron butterfly -1 1 1 -1 cr
5. (b− c) + (f− b) = f− c : 7 legs
2nd long call butterfly 1 -2 1 dr
+ 2nd short box -1 1 1 -1 cr
= 2nd long put iron butterfly -1 1 1 -1 cr
6. c+ (b− c) + (a− b) = a : 8 legs
3rd bull call 1 -1 dr
+ 2nd long call butterfly 1 -2 1 dr
+ 1st long call butterfly 1 -2 1 dr
= 1st bull call 1 -1 dr
7. b+ (a− b) + (e− a) = e : 9 legs
2nd bull call 1 -1 dr
+ 1st long call butterfly 1 -2 1 dr
+ 1st short box -1 1 1 -1 cr
= 1st bull put 1 -1 cr
8. c+ (b− c) + (f− b) = f : 9 legs
3rd bull call 1 -1 dr
+ 2nd long call butterfly 1 -2 1 dr
+ 2nd short box -1 1 1 -1 cr
= 2nd bull put 1 -1 cr
9. (b− c) + (a− b) + (e− a) = e− c : 10 legs
2nd long call butterfly 1 -2 1 dr
+ 1st long call butterfly 1 -2 1 dr
+ 1st short box -1 1 1 -1 cr
= long put iron condor -1 1 1 -1 cr
10. c+ (b− c) + (a− b) + (e− a) = e : 12 legs
3rd bull call 1 -1 dr
+ 2nd long call butterfly 1 -2 1 dr
+ 1st long call butterfly 1 -2 1 dr
+ 1st short box -1 1 1 -1 cr
= 1st bull put 1 -1 cr
with resulting spread ab can be identified with integer
solutions to the system Ax = ab, x ≥ 0, where com-
ponents of x represent multiplicities of main spreads
in the centipede x.
If m is the margin of b, then the margin of x is am.
Note that multiplicities of main spreads involved in
complex spreads are 1 or 0. Centipedes with a result-
ing spread ab can be considered as synthetic coun-
terparts of ab that are possible to build from main
spreads. We will relate centipedes to the same type
b if their resulting spreads are multiples of the same
main spread b.
ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems
326

4.2 Millipedes
Now we consider combinations of main spreads that
are market risk-free. They are based on the concept
of a horizontal spread, i.e., a long option combined
with a short option on the same underlying security
of the same type and exercise price. It is well-known
that such a spread is invariant to underlying security
market price changes and therefore market risk-free.
Lemma 1. A horizontal spread is market risk-free.
Proof Let us consider a horizontal call spread where
the long position in a call option lC and the short posi-
tion in a call option sC have the same exercise price e.
Each option contracts, say, 100 underlying units.
If sC is exercised, then the spread holder is obliged
to sell 100 underlying units to the holder of sC at the
price e. In this case, the spread holder can exercise lC,
i.e., buy 100 underlying units at the same price, and
deliver them to the holder of sC with no loss. If sC is
not exercised and lC is out-of-the-money, then lC can
be kept unexercised. A horizontal put spread has the
same hedging mechanism except that exercising put
options triggers the sell of underlying units.
Definition 5. A millipede is a set of main spreads
such that their linear combination with nonegative in-
teger coefficients is a zero spread.
Thus, 0 is a trivial millipede. This definition im-
plies that millipedes can be found as integer solutions
to the system Ax = 0, x ≥ 0, where x is the same
variable vector as in Section 4.1. A submillipede is
a subset of a millipede which is also a millepede. A
submillipede y of a millipede x is proper if 0 6= y 6= x.
Theorem 2. A millipede is market risk-free.
Proof Using induction on the number of components
of a millipede and Lemma 1, it is easy to verify that
the set of legs of a millipede can be partitioned into
pairs such that each pair is a horizontal call or put
spread. Therefore a millipede is a market risk-free
option combination.
Thus, the margin of a millipede is zero. There ex-
ists a simple relationship between centipedes and mil-
lipedes: if x is a centipede with the resulting spread
ab
i
, where b
i
is the ith column of A, and Ae
i
= b
i
,
then x− ae
i
is a millipede.
Definition 6. A millipede is minimal if it does not
contain proper submillipedes. A centipede is minimal
if it does not contain nontrivial millipedes. A cen-
tipede obtained from another centipede by deleting a
nontrivial millipede is a subcentipede.
We should notice that the absence of linear combi-
nations with negative coefficients in the definitions of
centipedes and millipedes does not affect the gener-
ality of these multi-leg option spreads because nega-
tions of main spreads are also main spreads. Thus,
a main spread b with negative coefficient − c can be
replaced by −b with positive coefficient c.
As mentioned in Section 2.2, the matrix A de-
fines a linear transformation of vectors in the port-
folio space to vectors in the spread space.
It is important to observe that the set of millipedes
is the kernel, the set of centipedes with the same re-
sulting spread is an equivalence class, the set of linear
combinations of main spreads is the image, and the
set of coefficient vectors of these combinations is the
coimage of this transformation.
5 USING CENTIPEDES AND
MILLIPEDES
As we show in this section, centipedes, as synthetic
counterparts of main spreads, can increase their profit
if the set of options with the same expiration date is
mispriced; while millipedes represent “white holes”
of option portfolios, i.e. a group of positions whose
margin is zero because, as shown in Section 4.2, mil-
lipedes are market risk-free option combinations.
5.1 Maximizing Option Arbitrage
Opportunities
Let p be the column vector of the prices of main
spreads including the transaction costs. Assume that
a main spread b is chosen for trading with quantity a.
Then a solution to
min{p
⊤
x : Ax = ab} (2)
answers the question whether there exist a synthetic
counterpart x of ab that is less expensive than ab.
If the answer is positive, then it is probably better
to trade the synthetic counterpart. Note that if ab is a
credit spread, then its synthetic counterpart can give
an advantage only if the minimum (2) is negative.
If ab is a multiple of a box spread, then solving
the above integer program, as we show in this section,
can maximize an option arbitrage opportunity. We
should note here that known arbitrage strategies in-
volving only options are based on box spreads which
are market risk-free; cf. (Cohen, 2005).
A long box spread is a debit spread because its
long (buy) side is more expensive than its short (sell)
side. The difference between the prices of these sides
is the long box spread price. An arbitrage opportunity
appears when the long box spread price is lower than
COMBINATIONS OF OPTION SPREADS
327

we
−r(τ−t)
, where w is the box spread width. i.e., the
amount that can be invested in a risk-free asset paying
interest r, where τ is the expiration date of the options
involved in the long box spread, and t is the present
date; cf. (Ronn and Ronn, 1989; Bharadwaj and Wig-
gins, 2001; Benzion et al., 2005). Therefore, catching
the arbitrage opportunity implies finding a long box
spread in the options market with a minimum price.
A short box spread is a symmetrical image of a
long box spread in relation to adjectives “long” and
“short”. Therefore, a short box spread is a credit
spread, i.e. of a negative price, and hence gives a risk-
free profit right on entering into it. Thus, catching an
arbitrage opportunity by a short box spread implies
finding a short box spread in the options market with
also a minimum but negative price.
The box spread arbitrage has been well studied.
A recent study and literature review can be found
in (Benzion et al., 2005). It is well-known that a box
spread is a synthetic position in a short position in a
stock and a long position in the same stock. A box
spread can also be viewed as a synthetic position in
other option spreads as follows:
Definition 7. A synthetic box spread is a centipede
whose resulting spread is a multiple of a box spread.
Let p
b
be the price of a box spread b. We assume
that p
b
> 0 and then b is a long box (debit) spread,
or p
b
< 0 and then b is a short box (credit) spread.
We exclude the case p
b
= 0 which means an obvious
error in pricing of options.
Let x
∗
be the synthetic box spread with the result-
ing spread a
∗
b that is found by solving the integer
program (2) with variables x and 1 ≤ a ≤ a
max
, where
a
max
is a chosen multiplicity upper bound.
As a multiple of a box spread is a trivial synthetic
box spread, p
⊤
x
∗
≤ a
∗
p
b
. We assume that a
∗
p
b
> 0
implies p
⊤
x
∗
> 0; otherwise we have again an obvi-
ous error in pricing of options. Thus, if a
∗
b gives
an arbitrage opportunity, then its synthetic counter-
part x
∗
gives a better arbitrage opportunity only if
p
⊤
x
∗
< a
∗
p
b
.
While a box spread can find an arbitrage opportu-
nity by capturing only four mispriced options, a syn-
thetic box spread is a much more powerful tool be-
cause it captures mispriced options in the whole op-
tion chain.
5.2 Decompositions of Option Portfolios
Let us recall that, according to the definition given in
Section 2.2, a portfolio of main spreads is an in-
teger column vector of size n whose components q
i
represent quantities of main spreads. Thus, if m
i
is
the margin of main spread i, then m
i
q
i
is the margin
of the ith component of the portfolio, where 1 ≤ i ≤ n.
We assume that q
i
> 0 implies that the portfolio
has a position in main spread i with quantity q
i
and
that q
i
= 0 implies that the portfolio has no position
in the main spread i.
Let us introduce the following constant vectors:
m
⊤
= ( m
1
m
2
··· m
n
)
q
⊤
= ( q
1
q
2
··· q
n
)
1
⊤
= ( 1 1 ··· 1 )
and the followingnonnegativeinteger variablevectors
a
⊤
= ( a
1
a
2
··· a
n
)
x
i
⊤
= ( x
i1
x
i2
··· x
in
)
y
j
⊤
= ( y
j1
y
j2
··· y
jr
)
z
⊤
= ( z
1
z
2
··· z
r
)
where components of a are associated with multiplic-
ities of main spreads that are not necessarily in the
portfolio, components of x
i
and y
j
are associated with
multiplicities of main spreads in centipedes and milli-
pedes, respectively, that are in the portfolio, and com-
ponents of z are 0-1 variables for counting minimal
millipedes in the portfolio. We assume that r = ⌊n/2⌋
because a nontrivial millipede involves at least two
main spreads, hence 1 ≤ j ≤ r.
We also consider the nonnegative integer variable
vector
y
⊤
= ( y
1
y
2
··· y
r
)
instead of the vectors y
j
in portfolio decompositions
with a single millipede.
Now we show how the no-offset margin m
⊤
q of
the portfolio q can be reduced to obtain an offset mar-
gin of this portfolio using centipedes and millipedes
as offsets. As we show in this section, the reduction
follows from a decomposition of the portfolio into
centipedes and millipedes.
Let b be a main spread. We say that the portfo-
lio q contains a centipede or millipede x with the re-
sulting spread ab, where a > 0 or a = 0, respectively,
if Ax = ab and x ≤ q. Centipedes and/or millipedes
x
1
,x
2
,...,x
s
generate a decomposition of the portfo-
lio q if x
1
+ x
2
+ ... + x
s
= q.
If µ
i
denotes the margin of the ith component of
this decomposition, where µ
i
= 0 if x
i
is a millipede,
then µ
1
+ µ
2
+ ... + µ
s
is the decomposition margin.
Lemma 2. Any decomposition of an option portfo-
lio into centipedes and millipedes can be transformed
into a decomposition with at most n nonzero compo-
nents, at most one centipede of each type, and the
same decomposition margin.
ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems
328

Proof We can sum up centipedes of each type, arbi-
trarily add to these sums all nontrivial millipedes, if
any, and thus obtain a decomposition with at most n
nonzero components. The margin of the sum x
i
+ x
j
is µ
i
+ µ
j
, therefore the new decomposition has the
same margin.
To obtain a maximum reduction of the marginm
⊤
q
using centipedes and millipedes as offsets we can de-
compose the portfolio q as follows.
Let b
i
be the ith main spread, i.e., the ith column
of A, and let {a,x
1
,x
2
,...,x
n
,} be the variable set.
Then the set of solutions to the system
Ax
i
= a
i
b
i
, 1 ≤ i ≤ n
n
∑
i=1
x
i
= q
(3)
defines a set of decompositions of the portfolio q that
contains, by Lemma 2, a decomposition with a mini-
mum margin. Note that setting a = q and x
i
= q
i
e
i
for
all i gives a trivial solution to this system.
It is important to observe that a solution to the sys-
tem (3) defines a portfolio a from the coimage of the
transformation by the matrix A. The no-offset mar-
gin of a, i.e., m
⊤
a, is the offset margin of q. Since a
carries the same risk profile as q we call it a represen-
tative of q for the decomposition x
1
,x
2
,...,x
n
.
Note that a is not always a subportfolio of q be-
cause the inequality a ≤ q may not hold. If it holds,
then we call a a proper representative of q.
Lemma 3. If a is a representative of q, then q − a is
a millipede.
Proof Multiplying the lower equation in (3) by A
from the left and using the upper equation we obtain
Aa =
n
∑
i=1
a
i
b
i
= Aq
which implies A(q− a) = 0.
Obviously, if a is a proper representative of q, then
the millipede q− a is a subportfolio of q.
Definition 8. A solution a
∗
,x
∗
1
,x
∗
2
,...,x
∗
n
to the inte-
ger program of minimizing the objective
m
⊤
a (4)
under the constraints (3) defines a main decomposi-
tion x
∗
1
,x
∗
2
,...,x
∗
n
of the portfolio q and a main repre-
sentative a
∗
of q for this decomposition.
The following theorem establishes that the mar-
gin of a main decomposition cannot be reduced using
centipedes and millipedes as offsets.
Theorem 3. A main representative of a main repre-
sentative of q is also a main representative of q.
Proof Let a
′
be a main representativeof a
∗
for the de-
composition x
′
1
,x
′
2
,...,x
′
n
. Obviously, m
⊤
a
′
≤ m
⊤
a
∗
.
Then it is not hard to verify that a
′
is also a represen-
tative of q for the decomposition x
′′
1
,x
′′
2
,...,x
′′
n
, where
x
′′
i
= x
∗
i
+ x
′
i
− a
∗
i
e
i
for all i. Therefore, m
⊤
a
′
= m
⊤
a
∗
, and hence a
′
is a
main representative of q.
A main decomposition contains millipedes not
only among its own millipedes but also inside its cen-
tipedes which, therefore, may not be minimal. How-
ever, solving the following modified version of the
problem (3)(4) we can extract all millipedes from the
centipedes that are not minimal and collect all milli-
pedes in a single subportfolio we call a white hole.
Let {a,x
1
,x
2
,...,x
n
,y} be the variable set. Then
the set of solutions to the system
Ax
i
= a
i
b
i
, 1 ≤ i ≤ n, Ay = 0
n
∑
i=1
x
i
+ y = q
(5)
defines a set of decompositions of q that contains all
main decompositions.
Definition 9. A solution a
◦
,x
◦
1
,x
◦
2
,...,x
◦
n
,y
◦
to the in-
teger program of minimizing the objective
m
⊤
a−
1
⊤
y
1
⊤
q
(6)
under the constraints (5) defines a white-hole de-
composition of the portfolio q into centipedes, which
are nonzero vectors among x
◦
1
,x
◦
2
,...,x
◦
n
, and a milli-
pede y
◦
, which is a white hole in q.
As the following lemma and theorem state, a
white-hole decomposition is just an extension of a
main decomposition by one component collecting all
millipedes; hence, a white-hole decomposition has
only one millipede and only minimal centipedes.
Lemma 4. The vectors x
◦
1
,x
◦
2
,...,x
◦
n
are either mini-
mal centipedes or zero vectors.
Proof Let a centipede x
◦
i
be not minimal, and let v be
a nontrivial millipede in x
◦
i
. Then moving v from x
◦
i
to y
◦
adds value
−m
⊤
v−
1
⊤
v
1
⊤
q
to the objective (6). As 1
⊤
v > 0, the objective would
decrease, which is a contradiction.
Let x
◦
i
> 0 be not a minimal centipede. Then it is
a nontrivial millipede that could be added to y
◦
and
decrease the objective again.
COMBINATIONS OF OPTION SPREADS
329

Theorem 4. m
⊤
a
◦
= m
⊤
a
∗
, i.e., x
◦
1
,x
◦
2
,...,x
◦
n
is a
main decomposition, and hence a
◦
is a main repre-
sentative of q, where q− a
◦
± y
◦
is a millipede.
Proof If y
◦
= 0, then the equation m
⊤
a
◦
= m
⊤
a
∗
is
evident. Assume that y
◦
> 0.
Let y
∗
be the sum of all millipedes inside and
among x
∗
1
,x
∗
2
,...,x
∗
n
. Note that y
◦
> 0 implies y
∗
> 0
and that x
◦
1
,x
◦
2
,...,x
◦
n
+ y
◦
is a decomposition with
margin m
⊤
a
◦
≥ m
⊤
a
∗
; otherwise x
∗
1
,x
∗
2
,...,x
∗
n
is not
a main decomposition.
If m
⊤
a
◦
> m
⊤
a
∗
, then
m
⊤
a
∗
≤ m
⊤
a
◦
− 1 ≤ m
⊤
a
◦
−
1
⊤
y
◦
1
⊤
q
because y
◦
≤ q. As m
⊤
a
∗
−
1
⊤
y
∗
1
⊤
q
< m
⊤
a
∗
, we have
m
⊤
a
∗
−
1
⊤
y
∗
1
⊤
q
< m
⊤
a
◦
−
1
⊤
y
◦
1
⊤
q
Thus, x
◦
1
,x
◦
2
,...,x
◦
n
,y
◦
is not a white-hole decomposi-
tion, which is a contradiction.
By Lemma 3, q − a
◦
is a millipede, therefore
q − a
◦
± y
◦
is a millipede because it is a sum of two
millipedes, q− a
◦
and ±y
◦
.
A white-hole decomposition partitions a given
portfolio into two subportfolios that can be indepen-
dently closed without affecting the risk profiles of
each other. A white hole can be closed because the
residual portfolio can be more attractive for returns
or, vice versa, because the white hole is risk-free.
Providing the finest partition of the residual port-
folio into minimal centipedes (that can also be closed
independently), a white-hole decomposition leaves
the structure of the white hole unclear. Solving the
following integer program, however, decomposes a
white hole into minimal millipedes.
Let y
1
,y
2
,...,y
r
,z be the variable set. Then the set
of solutions to the system
Ay
j
= 0, 1
⊤
y
j
≥ z
j
, 1 ≤ j ≤ r
r
∑
j=1
y
j
= y
◦
(7)
defines all decompositions of the white hole y
◦
into at
most r millipedes.
A solution y
†
1
,y
†
2
,...,y
†
r
,z
†
to the integer program
of maximizing the score 1
⊤
z under the constraints (7)
defines a decomposition of the white hole y
◦
into
1
⊤
z nontrivial millipedes, which are nonzero vectors
among y
†
1
,y
†
1
,...,y
†
r
.
Definition 10. a
◦
, x
◦
1
,x
◦
2
,...,x
◦
n
, y
†
1
,y
†
2
,...,y
†
r
, z
†
de-
fine a main representative a
◦
and a prime decompo-
sition of the portfolio q into centipedes, which are
nonzero vectors among x
◦
1
,x
◦
2
,...,x
◦
n
, and 1
⊤
z non-
trivial millipedes, which are nonzero vectors among
y
†
1
,y
†
2
,...,y
†
r
.
The followingtheorem establishes that a prime de-
composition of an option portfolio is a finest decom-
position that completely reveals its structure in terms
of centipedes and millipedes.
Theorem 5. All centipedes and millipedes in a prime
decomposition are minimal.
Proof Lemma 4 implies that all centipedes in a prime
decomposition are minimal. Let us show that all non-
trivial millipedes in there are also minimal.
Let a nontrivial millipede y
†
k
be not minimal.
Then y
†
k
contains a proper submillipede v and hence
u = y
†
k
− v is also a proper submillipede.
Besides, there exists a positive integer l < r such
that y
†
l
= 0 and hence z
†
l
= 0; otherwise each milli-
pede among y
†
1
,y
†
2
,...,y
†
r
is minimal and contains two
components. Then we can construct a new decom-
position replacing y
†
k
, y
†
l
and z
†
l
with y
‡
k
= u, y
‡
l
= v,
and z
‡
l
= 1, where y
‡
k
+ y
‡
l
= y
†
k
. This replacement de-
creases the number of nontrivial millipedes by one,
which is a contradiction.
5.3 Decompositions with Proper
Representatives
It is not hard to verify that all results obtained in Sec-
tion 5.2 remain valid if the systems (3) and (5) are
complimented by the inequality a ≤ q. Thus, there
exist counterparts of main, white-hole and prime de-
compositions with proper representatives. The option
trader can be interested in this kind of decomposi-
tions because the conversion of the portfolio q into its
proper representative a requires only selling the sub-
portfolio q− a. While the conversion into a represen-
tative, which is not proper, requires selling quantities
q
i
− a
i
from positions i with q
i
> a
i
, buying quantities
a
j
− q
j
for positions j with a
j
> q
j
> 0 and open-
ing new positions k with quantities a
k
if a
k
> q
k
= 0.
Considering only proper main representatives, how-
ever, can reduce savings on margin; see Section 6.
6 COMPUTATIONAL
EXPERIMENT
Now we are conducting the computational study on
finding option arbitrage opportunities by synthetic
box spreads and the estimation of margin reductions
ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems
330

for portfolios of main spreads by white-hole decom-
positions using ILOG CPLEX 12.1 for solving integer
programs. We present here only preliminary results.
We experimented with the option chains for differ-
ent stocks provided by www.google.com/finance and
did not detect an option arbitrage. It is not surprising
because the price quotes in this web site are delayed
by 15 minutes, while option arbitrage opportunities
usually last for seconds; cf. (Bharadwaj and Wiggins,
2001; Benzion et al., 2005).
Using the same web site we also estimated the av-
erage savings on margin by replacing randomly gen-
erated portfolios of different sizes by their main rep-
resentatives. The results are presented on Fig. 1.
3 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32
10%
20%
30%
40%
50%
60%
70%
M
P
Figure 1: The percentage of average savings on margin by
main (M) and proper main (P) representatives of over 500
portfolios of main spreads of each size from 3 to 32. All the
main spreads were on the exercise domain of size 10 and ex-
ercise differential of $5USD. The portfolios were generated
by proportional random sampling with replacement based
on the trading volume of options on NASDAQ:AAPL ex-
piring on 22-OCT-2011. The options data were taken from
www.google.com/finance on 04-AUG-2011 when the under-
lying security price was at $377.37USD.
7 CONCLUSIONS
This paper takes only the first step in studying combi-
nations of option spreads and demonstrates how these
combinations can be used in trading and margining
practice. An important consequence of this study is
a sketch of a combinatorial theory of option port-
folios that we believe will be useful for developing
new techniques for high-frequency trading and new
margining methodologies.
Our next step will be devoted to computational ex-
periments for detecting option arbitrage opportunities
using live option price quotes and estimating margin
reductions for portfolios of main spreads with differ-
ent underlying stocks.
REFERENCES
Benzion, U., Danan, S., and Yagil, J. (2005). Box spread
strategies and arbitrage opportunities. J. Derivatives,
12(3):47–62.
Bharadwaj, A. and Wiggins, J. B. (2001). Box spread and
put-call parity tests for the S&P 500 index LEAPS
market. J. Derivatives, 8(4):62–71.
CBOE (2003). Regulatory Circular RG03-066. August 13.
CBOE (2004). Regulatory Circular RG04-90. August 16.
CBOE (2005). Regulatory Circular RG05-37. April 6.
Cohen, G. (2005). The bible of options strategies. Financial
Times Prentice Hall. Pearson, New Jersey.
Curley, M. T. (2008). Margin trading from A to Z. John
Wiley & Sons, New Jersey.
IDA (2007). Bulletin 3654.
Matsypura, D. and Timkovsky, V. G. (2011). Margining
option portfolios by network flows. Networks. DOI
10.1002/net.
McMillan, L. G. (2002). Options as a strategic investment.
Prentice Hall, 4 edition.
Ronn, A. G. and Ronn, E. I. (1989). The box-spread arbi-
trage: theory, tests and investment strategies. Review
of Financial Studies, 2(1):91–108.
SEC (2005). Release 34-52738.
COMBINATIONS OF OPTION SPREADS
331