SECURE DELIVERY OF DATA IN WSN

Ibrahim Kamel and Hussam Juma

University of Sharjah, Department of Electrical and Computer Engineering, Sharjah, U.A.E.

Keyword: Sensor Network, Watermarking, Data Integrity.

Abstract: This paper proposes FWC- a hash-based fragile watermarking technique to protect the integrity of sensor

data. Sensor data are organized into groups before calculating the hash digest and storing them in the least

significant bits. The watermark is chained across the groups to mitigate group insertion and deletion attacks.

Detailed security analysis is provided for each of the proposed scheme. Experimental results prove that the

proposed schemes are much faster than SGW security technique. At the same time, the proposed schemes

are more robust than SGW.

1 INTRODUCTION

Wireless sensor network (WSN) is an array

(possibly very large) of sensors that are small in

size, have limited computing capabilities and

on securing sensor networks use traditional security

solutions that are based on cryptographic algorithms

and digital signatures (Perrig et al., 2006), they are

not suitable for sensors.

Watermarking algorithms are much lighter and

require less power and processing capabilities (Ling

et al., 2011). Thus, watermarking is more suitable

for WSNs. The main idea of digital watermarking is

to embed a piece of secret information (the

watermark) into the data stream in such a way that

any change or tamper with the original data would

corrupt the watermark. This type of watermarking is

called fragile watermarking as opposed to robust

watermarking that is used mainly for copyright

protection.

This paper proposes a fragile watermarking

scheme to verify integrity of data in WSNs. The

proposed technique FWC can be considered as an

improvement for the technique proposed by Guo

(Guo et al., 2007) for data streams, which is referred

to as Sliding Group Watermark (SGW) in this paper.

In the performance and security analysis section

SGW will be used as a yardstick to show the merit

of the proposed technique.

In SGW for each data element S

the algorithm

calculates the hash value using the hash function

HASH() and a secret key K that is known to the

sender and receiver only. The size of the group is

determined adaptively as a function of the data itself.

The data readings that determine the end of the

groups are called synchronization points. For each

data element S

in the group, a hash value h

applying the hash function HASH() along with the

secret key K, h

= HASH (S

|| K). if (h

mod m) = 0

then S

is a synchronization point and it marks the

end of a group. A group hash value is then computed

as the hash of the concatenation of all hash values of

data elements in the group as in Figure 1.

= HASH (K||[HASH(K||S

)||…||HASH(K||S

)])

i+1

= HASH (K||[HASH(K||S

Z1+1

)||…

||HASH(K||S

Z1+ Z2

)])

W = HASH ([K||g

||g

i+1

)])

The watermark W is formed using the hash function

HASH() which is applied to the concatenation of the

current group hash value group g

and next group

hash value group g

i+1

. The watermark W is then

embedded by replacing the least significant bit of the

data elements with the watermark bits.

The watermark calculation in SGW becomes

expensive, especially when the group size is large.

There is no proof that repeated calculation of the

secure hash function in the calculation of the

watermark in SGW would improve the security of

the hash function. In

Juma et al., (2008) we proposed

S-SGW, which is a simplification of the SGW. S-

SGW optimizes and reduces the need for repeated

use of the secure hash function. Another important

limitation of SGW and S-SGW is that the insertion

and deletion attacks can create ambiguity at the

server side. When such attacks occur the receiver

Kamel I. and Juma H..

SECURE DELIVERY OF DATA IN WSN.

DOI: 10.5220/0003806000830086

In Proceedings of the 1st International Conference on Sensor Networks (SENSORNETS-2012), pages 83-86

ISBN: 978-989-8565-01-3

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

may lose track of the synchronization points. In most

of the cases the receiver will not be able to construct

the same groups formed by the sender and

consequently will not be able to reconstruct the

watermarks correctly, and thus the data will be

rejected. This paper proposes FWC, which

overcomes the above two limitations. FWC is faster

and requires much less battery power than both

SGW and S-SGW.

Figure 1: SGW watermark embedding process.

2 FRAMEWORK OF THE

PROPOSED SCHEMES

The proposed schemes organize the sensor data

elements S

, S

, … , etc. into groups g

, g

… , etc. of variable sizes. The size of the group is

determined adaptively as a function of the data itself

= (S

|| S

||…|| S

)

= (S

Z1+1

||…|| S

Z1+Z2

)

= (S

1+Z2+1

||…|| S

1+Z2+Z3

)

(1)

The proposed scheme uses the hash function

HASH() which is applied to the concatenation of all

individual data elements in the group along with the

secret key K that is known to the sender and

receivers only to compute the watermark. The

computed watermark is then embedded by replacing

the least significant bit of the data reading of the

group. To ensure the completeness of the data

groups, the watermark is chained across every two

groups so that it is more difficult for the attacker to

insert or delete a complete group without detection.

To verify the integrity of the received group, the

receiver reconstructs the watermark and checks

against the extracted watermark. If the two

watermarks match, the group is considered

authentic; in case of a mismatch, the group is

reported as not authentic. HASH() a secure hash

function such as MD5 or SHA. We use variable

group size for better security. The group is

determined random number generator.

3 FORWARD WATERMARK

CHAIN (FWC) SCHEME

The structure of the data elements as well as the

watermark construction in SGW (Guo et al., 2007) is

complex. Moreover, the sender and receiver need to

create a large amount of memory (called buffers) to

store at least two groups of data. WSNs usually have

limited computing and battery power, and thus we

propose an FWC scheme to reduce and simplify the

structure of the data elements and watermark

construction.

Figure 2 gives an overview on the FWC scheme.

The FWC scheme is simpler, faster and requires

much less battery power which makes it more

suitable for WSNs than SGW. FWC uses variable

group size because it is more robust (secure) than

when using a constant group size. However, FWC

uses a random number generator algorithm to

generate sequences of numbers that can be used to

determine the group size instead of using

synchronization points. The pseudo-random number

generator uses a secret key K as a seed that is known

to the sender and receivers only. This makes it more

difficult for attackers to determine the group size.

Using the same seed value (secret key K) at the

receiver side, the same sequence of groups sizes are

reproduced.

Figure 2: FWC scheme embedding process.

= HASH (K || g

) (2)

FWC simplifies the watermark construction by

applying the hash function HASH() to one group

each time. The resulting watermark is then stored in

the earlier group. This way the watermark is chained

across every two groups, making it more difficult for

the attacker to insert or delete a complete group.

FWC can be implemented with either constant group

size or variable group sizes.

3.1 FWC Embedding Algorithm

The FWC embedding algorithm consists of two

processes: grouping and embedding. First, FWC

uses a pseudo-random number generator along with

a secret key K known only to the sender and the

SENSORNETS 2012 - International Conference on Sensor Networks

receivers to determine the group sizes. Second, when

two such groups g

i-1

and g

are formed, the group g

watermark W is computed using HASH() which is

applied to the concatenation of all individual data

readings in the group. After computing the g

watermark, the sender needs to extract the right

number of bits from the watermark W equal to the

number of data elements in group g

i-1

. If the number

of data elements in group g

i-1

is greater than the

length of the computed watermark W, then the

watermark W is concatenated to itself until its size is

equal to the number of data elements in group g

i-1

The computed watermark W of group g

is then

embedded in group g

i-1

by replacing the least

significant bits of all data elements in group g

i-1

. In

this way, the embedded watermark is chained across

every two groups. So if the whole group is inserted,

the insertion can be easily detected. Once the

watermark is embedded, the group g

i-1

is sent to the

receiver.

3.2 FWC Detection Algorithm

To verify the integrity of the received groups, the

receiver uses the same pseudo-random number

generator along with the secret key K to reproduce

the group size. Then the receiver organizes the

received data into groups similar to those formed by

the sender. We assume that group g

i-1

is formed prior

to group g

. Remember that the watermark of group

is stored in group g

i-1

. Then the watermark of

group g

is reconstructed and checked against the

extracted watermark from group g

i-1

. If the two

watermarks match, then group g

is designated as

being authentic and the data of group g

is accepted.

In the event that the two watermarks do not match,

then the detection algorithm assumes that group g

has been altered during the transmission and thus

rejects the data elements of group g

4 FWC SECURITY ANALYSIS

The attacker’s goal is to make undetectable

modification to the data streams. In this analysis, we

assume that the attacker has only modified one or

more data items of group g

as in Figure 3. The first

scenario is in case the attacker only modifies the

least significant bits of group g

(Wg

i+1

). At the

receiver end, group g

matches the extracted

watermark (Wg

) from group g

i-1

. As a result, the

receiver will accept group g

. Since the attacker

alters Wg

i+1

, group g

i+1

will not match Wg

i+1

. Thus,

the receiver will consider g

i+1

as not authentic and

will reject it.

Figure 3: FWC data modification attack.

In the second scenario, we look at the possibility

that the attacker modifies the data of group g

while

not modifying the least significant bits of group g

This is shown in Figure 4.7. In this situation the

receiver will reject group g

. Since the attacker does

not change Wg

i+1

, group g

i+1

ends up matching

i+1

. Thus, the receiver will consider g

i+1

authentic.

In the third scenario, the attacker changes both

the data and the least significant bits of group g

(Wg

i+1

). As a result, the integrity check of groups g

and g

i+1

will fail and the receiver will therefore

reject both groups.

As a result of the current group modification

attack, the receiver will drop the current group or the

next group, or even both groups. FWC offers

significant performance advantages over the SGW

Section 5 shows simulation experiments that

compare FWC and SGW. WSNs usually have

limited computing and battery power, so it is

desirable to reduce the number of calculations.

Although FWC offers performance improvement

and watermark construction simplification over

SGW, it nonetheless suffers from the weaknesses of

SGW in the event of insertion and deletion attacks.

5 PERFORMANCE

EVALUATION

We performed experiments to measure the

performance and the overhead of applying the

proposed watermarking scheme. The experimental

results of the proposed FWC scheme are compared

with the SGW scheme.

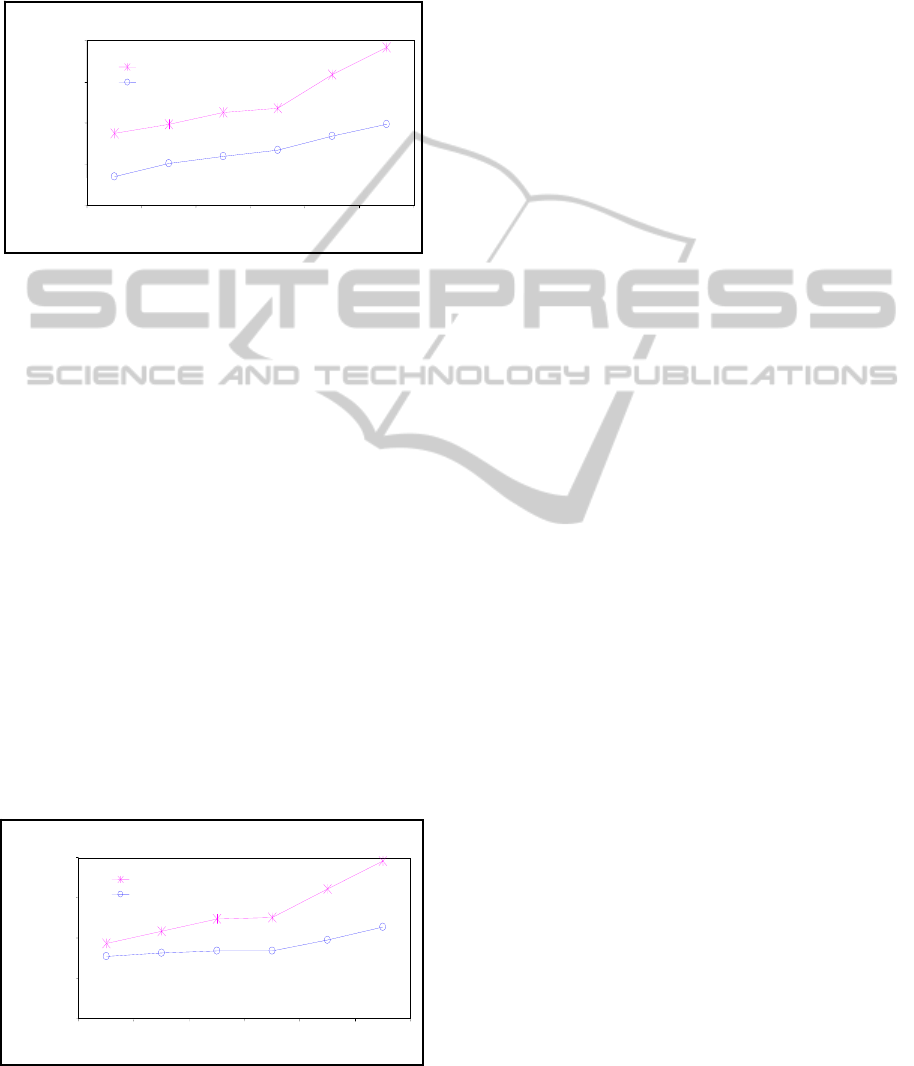
Figure 4 shows the average

embedding response time (Y) as a function of the

average window size (X). The figure shows that on

average SGW is about 73 times slower than the time

required by FWC. Hence FWC significantly

improves WSN response time, by more than one

order of magnitude.

Figure 5 shows the average extraction and

integrity check response time (Y) as a function of

the average window size (X). The figure shows that

SECURE DELIVERY OF DATA IN WSN

the FWC average extraction and integrity check

response time at average window size 1000 is about

45 times faster than SGW. Thus FWC significantly

improves WSN response time by much more than

one order of magnitude.

Figure 4: FWC randomly selected window size at sender

side.

6 CONCLUSIONS

We proposed the FWC scheme, which is much

simpler than SGW, and thus, it provides significant

performance improvements over SGW. FWC is

more robust than the SGW. Unlike SGW, FWC does

not lose track of group sizes under modification

attacks. This is because the group size in FWC is not

data dependent. Yet, FWC still might lose track of

group size in rare cases under insertion and deletion

attacks. The experimental results showed that our

proposed schemes have much less computational

overhead (one to two orders of magnitude compared

to the SGW scheme) and thus, can significantly

improve the WSN lifetime. In the future, we plan to

develop a semi fragile watermarking technique that

tolerates non-significant small changes, possibly

caused by communication interference, but detect

significant changes due to unauthorized alteration.

Figure 5: FWC randomly selected window size at the

receiver side.

ACKNOWLEDGEMENTS

The authors would like to thank Rasha Adnan for

helping in editing the paper.

REFERENCES

Guo H., Li Y., and Jajodia S. Chaining Watermarks for

Detecting Malicious Modifications to Streaming Data.

Information Sciences, vol. 177, no. 1, January 2007.

Juma, H. Kamel, I. Kaya, L., “On protecting the integrity

of sensor data”, the 15th IEEE International

Conference on Electronics, Circuits and Systems,

2008.

Kamel, I. and Guma, H. Simplified watermarking scheme

for sensor networks. International Journal of Internet

Protocol Technology, Inderscience, 2010.

H. Ling, L. Wang, F. Zou, Z. Lu, and P. Li. Robust video

watermarking based on affine invariant regions in the

compressed domain. Signal Processing, 2011.

Perrig A., Przydatek B., Song D. SIA: Secure Information

Aggregation in Sensor Networks. In Journal of

Computer Security, October, 2006.

Sion R., Atallah M., and Prabhakar S. Resilient Rights

Protection for Sensor Streams. 30th Int Conf VLDB,

pp.732–743, Toronto, Canada, Sept 2004.

1.00

10.00

100.00

000.00

50 100

150 200 500 1

000

AVG Window Size

AVG Extraction Time (msec)

FWC

1.00

10.00

100.00

1,000.00

10,000.00

50 100 150 200 500 1,000

FWC

AVG Window Size

AVG Embedding Time(msec)

SENSORNETS 2012 - International Conference on Sensor Networks