ANALYSIS OF MIMO SYSTEMS WITH ANTENNAS CORRELATION
WITH LINEAR AND NON-LINEAR SPATIAL DISTRIBUTION
Francisco Cano-Broncano
1
, C´esar Benavente-Peces
1
, Andreas Ahrens
2
,
Francisco Javier Ortega-Gonz´alez
1
and Jos´e Manuel Pardo-Mart´ın
1
1
Universidad Polit´ecnica de Madrid, Ctra. Valencia. km. 7, 28031 Madrid, Spain
2
Hochschule Wismar, University of Technology, Business and Design, Philipp-M¨uller-Straße 14, 23966 Wismar, Germany
Keywords:
Multiple Input Multiple Output, Channel Capacity, Bit-error Rate, Antennas Correlation, Wireless Communi-
cation.
Abstract:
Multiple input multiple output (MIMO) techniques for wireless communication systems have attracted in
the last years huge research activity due to the possibility of improving the link performance by increasing
the channel capacity and decreasing the bit-error rate (BER). In order to be able to define the benefits of
these MIMO techniques it is required to properly characterize the features of the communication channel in
the various properties and disturbances. Due to those effects, appropriate signal processing techniques are
needed to eliminate or diminish their effects. Furthermore, the use of multiple antennas both at the transmit
and the receive front-ends introduces a correlation effect between antennas due to their proximity producing
interference. In consequence, the BER increases and the channel capacity decreases. The goal of the present
contribution is to analyze the system performance under different spatial antennas distributions for Multi-User
(MU) MIMO systems in correlated fading channels.
1 INTRODUCTION
The MIMO term refers to a technique which takes
advantage of the spatial dimension of the underlying
wireless channel by using multiple antennas at both
the transmit (Tx) and the receive (Rx) sides trans-
mitting different data streams through each antenna
at the same time and the same frequency. Multiple
transmitting and receiving antennas are capable to re-
duce the error probability and increase the commu-
nication channel capacity without any bandwidth ex-
tensions. Since the capacity of MIMO systems in-
creases linearly with the minimum number of anten-
nas at both, the transmitter as well as the receiver side,
they have attracted substantial attention (McKay and
Collings, 2005), (Mueller-Weinfurtner,2002) and can
be considered as an essential part of increasing both
the achievable capacity and integrity of future gener-
ations of wireless systems (K¨uhn, 2006), (Zheng and
Tse, 2003).
The technical premise is to send different data sig-
nals through the various transmit antennas, but at the
same carrier frequency and the same time. In this
way, independent channels between different Tx and
Rx paths are formed to achieve spatial diversity or
space division multiplexing. Furthermore, this tech-
nique provides the possibility to choose the number of
bits per symbol to be transmitted through each path,
given a certain number of activated MIMO Tx-Rx
paths (layers) for exploiting the space dimension ob-
taining in this way a certain degree of freedom and
hence having the possibility to implement an adaptive
modulation scheme which depends on the particular
conditions of the activated layers (Zhou et al., 2005).
Multi-User MIMO (MU-MIMO) systems refers to
a link configuration comprising a base station with
multiple transmit and receive antennas providing ac-
cess to multiple users (fixed or mobile), each one
equipped with multiple antennas. The analysis de-
scribed in this paper focuses on the downlink seg-
ment.
MIMO systems have emerged as a promising
technique to achieve high transmission capacities in
wireless communication systems. MIMO systems
feature a stronger dependency with the propagation
channel conditions than single input single output
(SISO) systems present; however MIMO systems are
capable to reduce the bit-error probability and in-
crease the communication channel capacity by ex-
ploiting received multipath signals without increasing
278
Cano-Broncano F., Benavente-Peces C., Ahrens A., Javier Ortega-González F. and Manuel Pardo-Martín J..
ANALYSIS OF MIMO SYSTEMS WITH ANTENNAS CORRELATION WITH LINEAR AND NON-LINEAR SPATIAL DISTRIBUTION.
DOI: 10.5220/0003810102780283
In Proceedings of the 2nd International Conference on Pervasive Embedded Computing and Communication Systems (PECCS-2012), pages 278-283
ISBN: 978-989-8565-00-6
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

neither the required transmitted power nor the signal
bandwidth.
The communication channel is affected by var-
ious disturbances: attenuation, noise, interferences,
multipath, fading. Additionally, due to the prox-
imity of the multiple antennas at any of the ends,
the correlation effect appears affecting the channel
characteristics and pouring the communication link
performance. Several studies have been carried out
to characterize antenna correlation (Oestges, 2006;
Narasimhan, 2003; Asztly, 1996), providing models
which allow analyzing its effects on the communica-
tion system performance. Typically, in practical com-
munication systems, the separation between different
antennas at the base stations is set ten times the car-
rier wavelength while wireless mobile reception sta-
tion antennas are set to be separated by one carrier
wavelength to guarantee a proper link performance.
In order to reach the full MIMO system per-
formance, appropriate signal processing techniques
should be applied. A popular technique largely used
is the singular value decomposition (SVD) (Haykin,
2002). Through the appropriate use of such technique
at both the Tx and Rx sides performing some pre-
processing and post-processing respectively, channel
multipath interference as well as multi-user inter-
ferences can be eliminated (Benavente-Peces et al.,
2010). To obtain the full benefits of the SVD use, this
technique requires perfect channel state information
at both the transmitter and the receiver side, which
produces some communication overhead. The chan-
nel state has to be computed at the receiver side by
transmitting a training sequence and some overhead
is produced when delivering the channel state infor-
mation back to the transmitter side. The main contri-
bution of this work is the analysis of the downlink of a
MU-MIMO system under antennas correlation (Dur-
gin and Rappaport, 1999; Zelst and Hammerschmidt,
2002; Ahrens and Benavente-Peces, 2011).
The remaining part of this contribution is orga-
nized as follows: Section 2 describes the MU-MIMO
model including antenna correlation. Section 3 in-
troduces the spatial antenna distribution and models
two cases studies for demonstration purposes. The as-
sociated performance results are presented and com-
mented in section 4. Finally, in section 5 the conclud-
ing remarks are discussed.
2 MULTIUSER SYSTEM MODEL
The system model considered in this work consists of
a single base station (BS) supporting K mobile sta-
tions (MSs). The BS is equipped with n
T
transmit an-
tennas, while the kth (with k = 1,...,K) MS has n
Rk
receive antennas, i. e. the total number of receive an-
tennas including all K MSs is given by n
R
=
∑
K
k=1
n
Rk
.
The (n
Rk
×1) user specific symbol vector c
k
to be
transmitted by the BS is given by
c
k
=

c
k,1
,c
k,2
,...,c
k,n
Rk

T
. (1)
The vector c
k
is preprocessed before its transmission
by multiplying it by the (n
T
×n
Rk
) DL preprocess-
ing matrix R
k
and resulting the (n
T
×1) user-specific
transmit vector
s
k
= R
k
c
k
. (2)
After DL transmitter preprocessing, the n
T
-
component signal s transmitted by the BS to the
K MSs results in
s =
K
∑
k=1
s
k
= Rc , (3)
with the (n
T
×n
R
) preprocessing matrix
R = (R
1
,R
2
,...,R
K
) . (4)
In (3), the overall (n
R
×1) transmitted DL data vector
c combines all K DL transmit vectors c
k
(with k =
1,2,...,K) and is given by
c =

c
T
1
,c
T
2
...,c
T
K

T
. (5)
At the receiver side, the (n
Rk
×1) vector u
k
of the kth
MS is given by
u
k
= H
k
s+ n
k
= H
k
Rc+ n
k
. (6)
and can be expressed by
u
k
= H
k
R
k
c
k
+
K
∑
i=1,i6=k
H
k
R
i
c
i
+ n
k
, (7)
where the MSs received signals experience both
multi-user and multi-antenna interferences. In (6) and
(7), the (n
Rk
×n
T
) channel matrix H
k
connects the n
T
BS specific transmit antennas with the n
Rk
receive an-
tennas of the kth MS.
It is quite common to assume that the coefficients
of the (n
Rk
×n
T
) channel matrix H
k
are independent
and Rayleigh distributed with equal variance. How-
ever, in many cases correlations between the transmit
antennas as well as between the receiveantennas can’t
be neglected. There are several methods to model
and characterize the antenna signals correlation ef-
fects on the MIMO channel model in the Rayleigh
flat-fading channel case. In this work it is assumed
that the correlation among receive antennas is inde-
pendent of the correlation between transmit antennas.
ANALYSIS OF MIMO SYSTEMS WITH ANTENNAS CORRELATION WITH LINEAR AND NON-LINEAR
SPATIAL DISTRIBUTION
279

The way to include the antenna signal correlation ef-
fect on the MIMO channel model for Rayleigh flat-
fading like channels is described in (Durgin and Rap-
paport, 1999; Zelst and Hammerschmidt, 2002) and
results in
H
k
= H
1/2
Rx
·G·H
1/2
Tx
, (8)
where G is a (n
Rk
×n
T
) uncorrelated channel ma-
trix with independent, identically distributed com-
plex Gaussian zero-mean unit variance elements and
where (·)
1/2
stands for the square root of a matrix.
The (n
Rk
×n
Rk
) matrix H
Rx
is used to model the cor-
relation among the kth MS receive antennas. On the
other hand, the (n
T
×n
T
) transmit correlation matrix
H
Tx
models the correlation among the transmit anten-
nas.
The interference, which is introduced by the chan-
nel matrix H
k
, requires appropriate signal processing
strategies. A popular technique is based on the SVD
of the system matrix H
k
as described in (Ahrens and
Benavente-Peces, 2010). Therein, after pre- and post-
processing of the transmitted and received signal vec-
tors, the user-specific decision variables result in
y
k
= V
ku
P
k
c
k
+ w
k
, (9)
where interferences between the different antenna
data streams as well as MUI (multi-user interference)
imposed by the other users are avoided as shown
in (Ahrens and Benavente-Peces, 2010). In (9), the
(n
Rk
×n
Rk
) diagonal matrix V
ku
contains the non-
zero square roots of the eigenvalues of H
H
k
H
k
, e.g.,
V
ku
=






p
ξ
k,1
0 ··· 0
0
p
ξ
k,2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 ···
p
ξ
k,n
Rk






, (10)
and the user-specific (n
Rk
×n
Rk
) diagonal power al-
location matrix is given by
P
k
=






√
p
k,1
0 ··· 0
0
√
p
k,2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 ···
√
p
k,n
Rk






(11)
and simplifies to P
k
=
p
βI
n
Rk
×n
Rk
for the power
equal distribution case with the parameter
p
β taking
the transmit-power constraint into account as high-
lighted in (Ahrens and Benavente-Peces, 2010). Fi-
nally the additive, white Gaussian noise (AWGN)
vector is given by w
k
. The resulting system model is
depicted in Fig. 1 In order to transmit at a fixed data
rate while maintaining the best possible integrity, i. e.,
bit-error rate, an appropriate number of user-specific
c
(m)
k,ℓ
y
(m)
k,ℓ
w
(m)
k,ℓ
q
ξ
(m)
k,ℓ
q
p
(m)
k,ℓ
Figure 1: Resulting kth user-specific system model per
MIMO layer ℓ (with ℓ = 1, 2,... , n
Rk
) and per transmitted
symbol block m
Table 1: Investigated user-specific QAM transmission
modes
throughput layer 1 layer 2 layer 3 layer 4
8 bit/s/Hz 256 0 0 0
8 bit/s/Hz 64 4 0 0
8 bit/s/Hz 16 16 0 0
8 bit/s/Hz 16 4 4 0
8 bit/s/Hz 4 4 4 4
MIMO layers has to be used, which depends on the
specific transmission mode, as detailed in Table 1 for
the exemplarily investigated case in which a multiuser
system with two users is considered (n
Rk
= 4 (with
k = 1,2), K = 2,n
R
= n
T
= 8). In order to avoid
any signalling overhead, fixed transmission modes are
used in this contribution regardless of the channel
quality (Ahrens and Lange, 2008).
3 ANTENNAS’ SPATIAL
DISTRIBUTION
Spatial multiplexing is a method to reach the the-
oretical maximum channel capacity with a reason-
able implementation complexity. Spatial multiplex-
ing achieves the best performance in rich-scattering
channels in which the paths suffer from uncorrelated
fading (Narasimhan, 2003). In this contribution, we
analyze and simulate two different antennas spatial
distributions (linear and non-linear uniform anten-
nas distributions) for a MIMO system composed of
n
T
= 4 transmit and n
R
= 4 receive antennas (single-
user MIMO link, K = 1). The goal is showing the
high dependency of both separation and distribution
on the correlation degree and the impact of antennas
correlation on the communication link performance.
3.1 Antennas with Linear Spatial
Distribution
In this case it is considered that the antennas are lin-
early distributed and equally spaced where this spac-
ing is set to ∆
t
and ∆
r
(given in wavelength units) at
PECCS 2012 - International Conference on Pervasive and Embedded Computing and Communication Systems
280

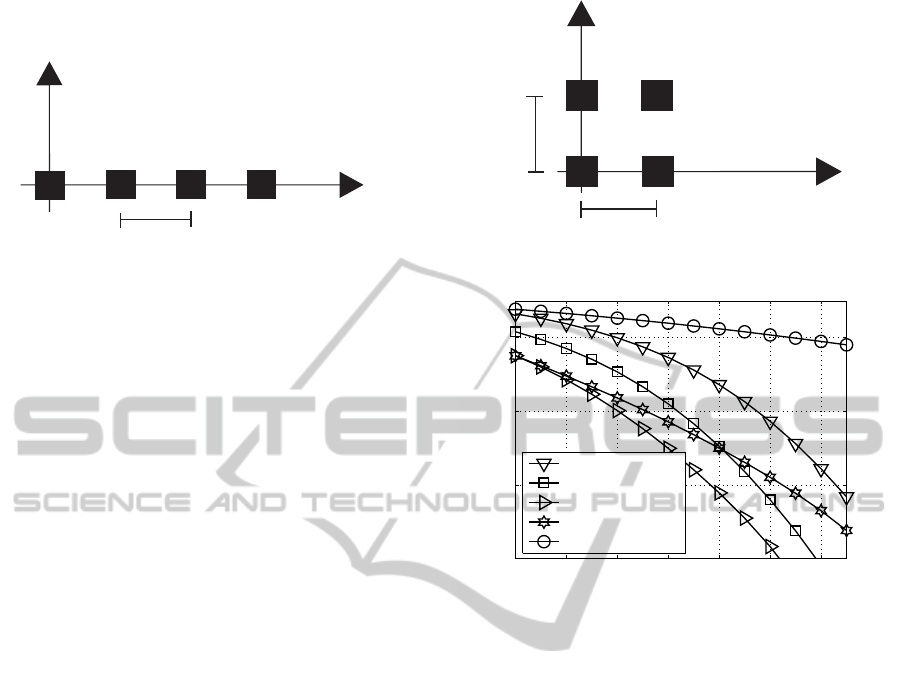
the transmitter and receiver side, respectively. Fig. 2
represents the antennas’ spatial distribution.
x/λ
y/λ
∆
Figure 2: Linear antennas distribution.
3.2 Antennas with Non-linear Spatial
Distribution
In this second case of study a non-linear antenna ar-
ray distribution with equal distance between adjacent
elements is assumed. We have imposed in this ex-
emplarily case that the chosen distribution is a square
with one antenna at each corner. Again, the imple-
mented MU-MIMO system contains n
T
= 4 transmit
and n
R
= 4 receive antennas (single-user MIMO link,
K = 1). Fig. 3 shows the geometrical disposition of
the antennas to be evaluated.
4 RESULTS
In this contribution a MIMO system in the absence
and the present of antenna correlation effects has
been analyzed including the consideration of linear
and non-linear antennas spacing for some exemplar-
ily fixed transmission modes (described in Tab. 1).
4.1 Single-user MIMO
Considering a frequency non-selective SDM (spatial
division multiplexing) single-user MIMO link (K =
1) composed of n
T
= 4 transmit and n
R
= 4 receive
antennas, the resulting BER curves are depicted in
Fig. 4 for the different transmission modes of Tab. 1,
when transmitting at a bandwidth efficiency of 8
bit/s/Hz.
Assuming a uniform distribution of the transmit
power over the number of activated MIMO layers, it
turns out that not all MIMO layers have to be acti-
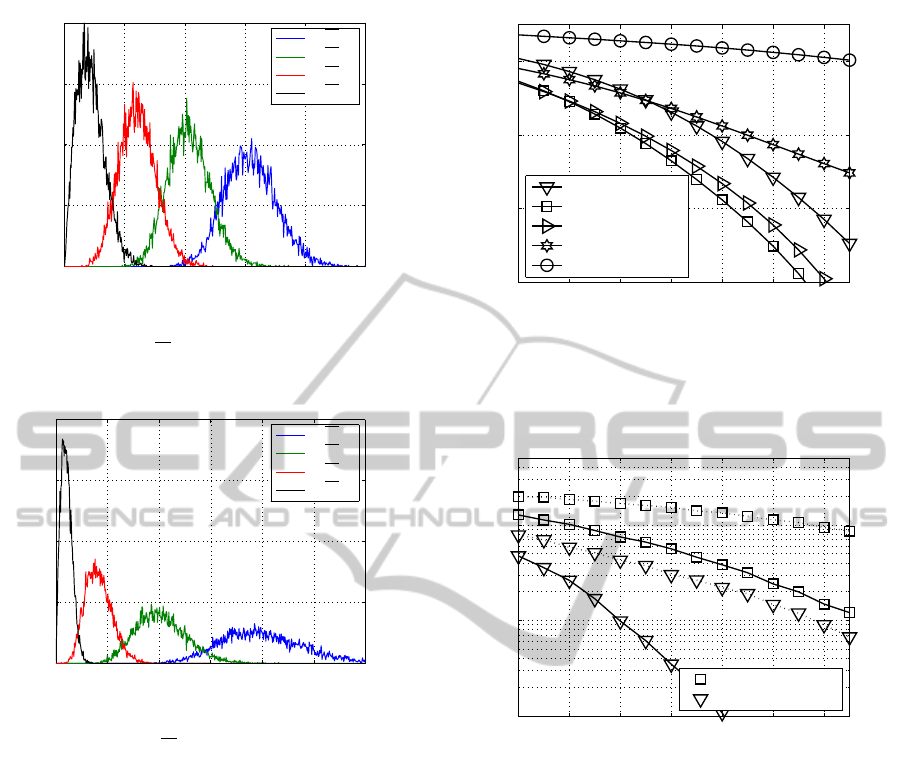
vated in order to achieve the best BERs. Fig. 5 shows
the probability density function (pdf) of the resulting
singular values in the case of an uncorrelated MIMO
channel with n
T
= 4 transmit and n
R
= 4 receive an-
tennas. When considering a single-user MIMO sys-
tem (K = 1) in the presence of antenna correlation,
x/λ
y/λ
∆
∆
Figure 3: Non-linear antennas distribution.
12 14 16 18 20 22 24
10
−8
10
−6
10
−4
10
−2
10 ·log
10
(E
s
/N
0
) (indB) →
bit-error rate →
(256,0,0, 0) QAM
(64,4,0, 0) QAM
(16,16,0, 0) QAM
(16,4,4, 0) QAM
(4,4,4 , 4) QAM
Figure 4: BER when using the transmission modes intro-
duced in Tab. 1 and transmitting 8 bit/s/Hz over uncorre-
lated frequency non-selective channels.
assuming a linear distribution of both the transmit and
receive antennas, and considering that the transmis-
sion is performed at a carrier frequency at 2.4 GHz
with an antenna separation at the transmit side (BS)
of 10 times the wavelength and an antenna separa-
tion at the receive side (MS) of 4 times the wave-
length, the resulting probability distribution function
of the computed singular values is depicted in Fig. 6.
Comparing the distribution of the singular-values de-
picted in Fig. 5 and 6, the correlation shifts the pdf of
the largest singular-value to higher values at the cost
of the remaining layers. In consequence, the probabil-
ity of using a reduced number of layers for transmit-
ting data becomes larger in the presence of antenna
correlation. Thus, taking the correlated MIMO chan-
nel instead of the uncorrelated one into consideration,
we observe that the influence of the layer with the
largest weighting factor increases.
Decreasing the distance between the receive an-
tennas increases the correlation effect. Fig. 8 high-
lights the resulting BER for some exemplarily trans-
mission modes (from those in Tab. 1) when dimin-
ishing the antennas spacing with respect to the pre-
vious cases. In comparison with the results in Fig. 7
ANALYSIS OF MIMO SYSTEMS WITH ANTENNAS CORRELATION WITH LINEAR AND NON-LINEAR
SPATIAL DISTRIBUTION
281

0 1 2 3 4 5
0
0.005
0.01
0.015
0.02
p
ξ
1
p
ξ
2
p
ξ
3
p
ξ
4
pdf →
singular value →
Figure 5: PDF (probability density function) of the layer-
specific amplitudes
p
ξ
ℓ
for uncorrelated frequency non-
selective MIMO channels.
0 1 2 3 4 5 6
0
0.01
0.02
0.03
0.04
p
ξ
1
p
ξ
2
p
ξ
3
p
ξ
4
pdf →
singular value →
Figure 6: PDF (probability density function) of the layer-
specific amplitudes
p
ξ
ℓ
for correlated frequency non-
selective MIMO channels (linear distribution of both the
transmit and receive antennas with ∆
t
= 10 and ∆
r
= 4).
it is concluded that the shorter the distance between
receive antennas the larger the BER and finally the
link performance. Furthermore, continuing with the
reasoning described above it is concluded that not all
MIMO layers must be activated in order to obtain the
best results. Concerning the relation between the best
performing transmission modes and the probability
distribution function of the singular values, the high
dependency of the transmission mode with the largest
singular value can be remarked. This dependency in-
creases with the correlation degree, the larger the cor-
relation the higher the dependency. In consequence,
as the correlation becomes stronger, the probability to
use a lower number of layers increases.
12 14 16 18 20 22 24
10
−8
10
−6
10
−4
10
−2
10 ·log
10
(E
s
/N
0
) (indB) →
bit-error rate →
(256,0,0, 0) QAM
(64,4,0, 0) QAM
(16,16,0, 0) QAM
(16,4,4, 0) QAM
(4,4,4 , 4) QAM
Figure 7: BER when using the transmission modes in-
troduced in Tab. 1 and transmitting 8 bit/s/Hz over corre-
lated frequency non-selective channels (linear distribution
of both the transmit and receive antennas with ∆
t
= 10 and
∆
r
= 4).
12 14 16 18 20 22 24
10
−3
10
−2
10
−1
10 ·log
10
(E
s
/N
0
) (indB) →
bit-error rate →
(16,4,4, 0) QAM
(64,4,0, 0) QAM
Figure 8: BER with linear antenna distribution (solid
line) and with non-linear antenna distribution (dotted line)
when using the transmission modes introduced in Tab. 1
and transmitting 8 bit/s/Hz over correlated frequency non-
selective channels (∆
t
= 10 and ∆
r
= 0,1).
4.2 Multi-user MIMO
The parameters of the exemplarily studied two-users
MIMO system are chosen as follows: n
Rk
= 4 (with
k = 1,2), K = 2,n
R
= n
T
= 8. The obtained user-
specific BER curves are depicted in Fig. 9 for the dif-
ferent QAM constellation sizes and MIMO configura-
tions in Tab. 1 and confirm the results obtained within
the single-user system (K = 1). Assuming a uniform
distribution of the transmit power along the number
of activated MIMO layers, it still turns out that not all
MIMO layers have to be activated in order to achieve
the best BERs.
PECCS 2012 - International Conference on Pervasive and Embedded Computing and Communication Systems
282

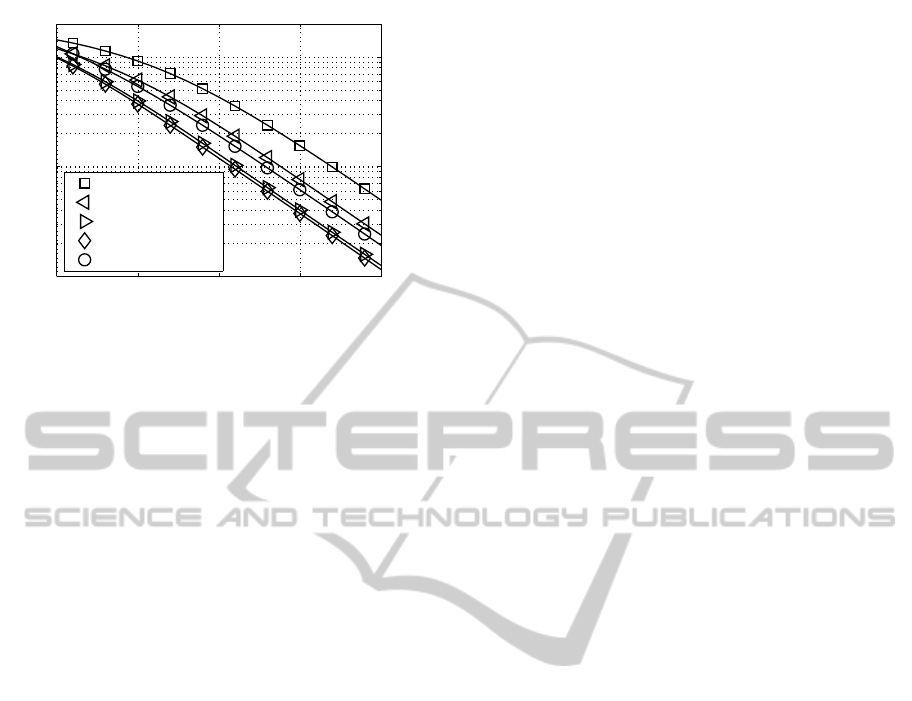
10 15 20 25 30
10
−3
10
−2
10
−1
10 ·log
10
(E
s
/N
0
) (indB) →
bit-error rate →
(256,0,0, 0) QAM
(64,4,0, 0) QAM
(16,16,0, 0) QAM
(16,4,4, 0) QAM
(4,4,4 , 4) QAM
Figure 9: SVD-based user-specific BERs when using the
transmission modes introduced in Table 1 and transmitting
8 bit/s/Hz over uncorrelated frequency non-selective chan-
nels.
5 CONCLUSIONS
This contribution has analyzed and simulated a MU-
MIMO system composed of n
T
transmit and n
R
re-
ceive antennas in conjunction with SVD-assisted sig-
nal processing and taking into account the correlation
effect among antennas both at the transmit and receive
sides. Additionally it was assumed a uniform distri-
bution of the transmit power along the MIMO system
activated layers.
By comparing the results obtained from computer
simulations it can be concluded that in the presence of
correlation among antennas, in the considered non-
linear spatial distribution (square spacing in the ex-
ample) the bit error rate increases for a given fixed
SNR (signal-to-noise-ratio), taking as reference the
case in which no correlation is present into consider-
ation. Moreover, that increment in the BER is larger
than the one produced when using an antenna linear
distribution affected by correlation.
Consequently, for a fixed bit-error rate the lin-
ear distribution is able to give better results than the
squared distribution. This is due to the reduction of
the dependency with neighbours antennas as the sep-
arations between them become larger. Additionally
we observe that for reaching the best performance it
is not required that all layers were activated.
REFERENCES
Ahrens, A. and Benavente-Peces, C. (2010). Modulation-
Mode and Power Assignment for SVD-assisted and
Iteratively Detected Downlink Multiuser MIMO Sys-
tems. In International Conference on Wireless Infor-
mation Networks and Systems (WINSYS), pages 107–
114, Athens (Greece).
Ahrens, A. and Benavente-Peces, C. (2011). Modulation-
Mode and Power Assignment for SVD-assisted
Downlink Multiuser MIMO Systems. In International
Conference on Pervasive and Embedded Computing
and Communication Systems (PECCS), pages 333–
338, Algarve (Portugal).
Ahrens, A. and Lange, C. (2008). Modulation-Mode and
Power Assignment in SVD-equalized MIMO Sys-
tems. Facta Universitatis (Series Electronics and En-
ergetics), 21(2):167–181.
Asztly, D. (1996). On Antenna Arrays in Mobile Commu-
nication Systems Fast Fading and GSM Base Station
Receiver Algorithms. PhD thesis, Royal Institute of
Technology, Stockholm.
Benavente-Peces, C., Cano-Broncano, F., Aust, S., and
Ahrens, A. (2010). Modulation-Mode Assignment
for SVD-assisted Multiuser MIMO Systems with
Correlations. In 18th International Conference on
Microwave, Radar and Wireless Communications
(MIKON), pages 415–418, Vilnius (Lithuania).
Durgin, G. D. and Rappaport, T. S. (1999). Effects of Multi-
path Angular Spread on the Spatial Cross-Correlation
of Received Voltage Envelopes. In IEEE Vehicu-
lar Technology Conference (VTC), pages 996–1000,
Houston, Texas, USA.
Haykin, S. S. (2002). Adaptive Filter Theory. Prentice Hall,
New Jersey.
K¨uhn, V. (2006). Wireless Communications over MIMO
Channels – Applications to CDMA and Multiple An-
tenna Systems. Wiley, Chichester.
McKay, M. R. and Collings, I. B. (2005). Capacity
and Performance of MIMO-BICM with Zero-Forcing
Receivers. IEEE Transactions on Communications,
53(1):74– 83.
Mueller-Weinfurtner, S. H. (2002). Coding Approaches for
Multiple Antenna Transmission in Fast Fading and
OFDM. IEEE Transactions on Signal Processing,
50(10):2442–2450.
Narasimhan, R. (2003). Spatial Multiplexing with Trans-
mit Antenna and Constellation Selection for Corre-
lated MIMO Fading Channels. IEEE Transactions on
Signal Processing, 51(11):28292838.
Oestges, C. (2006). Validity of the Kronocker Model for
MIMO Correlated Channels. In Vehicular Technology
Conference, volume 6, pages 2818–2822, Melbourne.
Zelst, A. v. and Hammerschmidt, J. S. (2002). A Single Co-
efficient Spatial Correlation Model for Multiple-Input
Multiple-Output (MIMO) Radio Channels. In 27th
General Assembly of the International Union of Ra-
dio Science, Maastricht.
Zheng, L. and Tse, D. N. T. (2003). Diversity and
Multiplexing: A Fundamental Tradeoff in Multiple-
Antenna Channels. IEEE Transactions on Information
Theory, 49(5):1073–1096.
Zhou, Z., Vucetic, B., Dohler, M., and Li, Y. (2005). MIMO
Systems with Adaptive Modulation. IEEE Transac-
tions on Vehicular Technology, 54(5):1073–1096.
ANALYSIS OF MIMO SYSTEMS WITH ANTENNAS CORRELATION WITH LINEAR AND NON-LINEAR
SPATIAL DISTRIBUTION
283