
FAST DEFORMATION FOR MODELLING
OF MUSCULOSKELETAL SYSTEM
Josef Kohout
1
, Petr Kellnhofer
1
and Saulo Martelli
2
1
Department of Computer Science and Engineering, University of West Bohemia, Plzeˇn, Czech Republic
2
Laboratorio di Tecnologia Medica, Istituto Ortopedico Rizzoli, Bologna, Italy
Keywords:
Deformation, Laplacian, Volume Preservation, Muscle Modelling.
Abstract:
This paper proposes a gradient domain deformation for wrapping surface models of muscles around bones
as they move during a simulation of physiological activities. Each muscle is associated with one or more
poly-lines that represent the muscle skeleton to which the surface model of the muscle is bound so that trans-
formation of the skeleton (caused by the movement of bones) produces transformation of the vertices of the
mesh subject to Laplacian linear constraints to preserve the local shape of the mesh and non-linear volume
constraints to preserve the volume of the mesh. All these constraints form a system of equations that is solved
using the iterative Gauss-Newton method with Lagrange multipliers. Our C++ implementation can wrap a
muscle of medium size in about a couple of ms up to 400 ms on commodity hardware depending on the type
of parallelization, whilst it can keep the change in volume below 0.04%. A preliminary biomechanical assess-
ment of the proposed technique suggests that it can produce realistic results and thanks to its rapid processing
speed, it might be an attractive alternative to the methods that are used in clinical practise at present.
1 INTRODUCTION
The musculoskeletal modelling and simulation is an
essential step in the process of looking for an opti-
mal strategy to provide patients suffering from vari-
ous musculoskeletal disorders, such as osteoporosis,
with better healthcare. The most common and tradi-
tional models (e.g. (Garner and Pandy, 2000), (Delp
and Loan, 2000)) assume that the muscle mechani-
cal action occurs along a poly-line, namely the action
line, joining origin and insertion points of the muscle,
i.e., sites at which the muscle is attached to the bone
by a tendon. Essentially, an action line is a represen-
tation of fibres in muscle-tendon unit.
When the muscle path is almost linear through-
out a motion, the action line can be defined as a sim-
ple straight line, otherwise, the action line is con-
sidered to be a poly-line passing through a num-
ber of intermediate via points, fixed to the under-
lying bone, so as to describe the muscle path in a
more realistic way (Jensen and Davy, 1975), (Arnold
et al., 2000), (van der Helm and Veenbaas, 1991)
or wrapping around wrapping surfaces, again fixed
to the underlying bone to geometrically constrain
the action line (Garner and Pandy, 2000), (Delp and
Loan, 2000), (Marsden and Swailes, 2008), (Any-
Body, 2010), (OpenSim, 2010) and (Audenaert and
Audenaert, 2008). In the most sophisticated mod-
els of this kind, action lines are considered as elastic
strings that can wrap automatically around multiple
surfaces, known as obstacles, which might be a set
of spheres, cylinders, ellipsoids or cones (Garner and
Pandy, 2000), a set of parallel contours (Gao et al.,
2002) or arbitrary volumetric data (Favre et al., 2010).
Although action line models are commonly used
in clinical practise (thanks to their processing speed),
in most of them an overestimation of predicted joint
loads is observable (Erdemir et al., 2007) and it has
been suggested that this overestimation is signifi-
cantly influenced by typical underestimation of the
muscle lever arm caused by the fact that these models
assume that the muscle fibre length is uniform over
the entire muscle bundle that is modelled, which is,
however, an assumption not often fulfilled in reality.
There are also much more complex models that
represent the muscles by 3D finite-element hexahe-
dral mesh whose vertices move in reaction to the
bones movement (Blemker and Delp, 2005). Each
cell of the mesh contains information about the di-
rection of the muscle fibres present in its volume by
mapping a cubical template of fibre architecture into
the muscle mesh. When the mesh changes, so do the
16
Kohout J., Kellnhofer P. and Martelli S..
FAST DEFORMATION FOR MODELLING OF MUSCULOSKELETAL SYSTEM.
DOI: 10.5220/0003811100160025
In Proceedings of the International Conference on Computer Graphics Theory and Applications (GRAPP-2012), pages 16-25
ISBN: 978-989-8565-02-0
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

paths of the fibres, i.e., muscle volume is wrapped
around bones as they move in this model. A good
agreement was found comparing the model results
with static MRI images taken in different postures
and it was showed that the muscle fibre deforma-
tions are highly non-uniform over the muscle vol-
ume. Finite-element based techniques, however, re-
quire large computational time and, therefore, they
are not suitable for clinical practise.
In our previous work (Kohout et al., 2011), we at-
tempted to bridge the gap between both approaches
proposing a musculoskeletal model that is fast enough
for use in clinical practise and for which it is rea-
sonable to expect that the prediction of the muscle
lever arm and the actual fibre length will be some-
where in between predictions by action-line methods
and more accurate finite-element methods. In this
model, a muscle is represented by a chaff of mus-
cle fibres that are automatically generated in the vol-
ume defined by its surface mesh which itself automat-
ically wraps around bones as they move. The wrap-
ping process is based on the mesh skinning technique
described by (Blanco and Oliveira, 2008) that is com-
bined with a post-adjustment of mesh vertices to min-
imise the changes in volume following the idea pre-
sented by (Aubel and Thalmann, 2000). The decom-
position of wrapped volume into muscle fibres is done
by a slice-by-slice morphing of predefined fibres tem-
plate into the wrapped muscle exploiting mean value
coordinates (Ju et al., 2005). A muscle of medium
size can be processed in a fast speed of one second on
commodity hardware, however, for some muscles, the
maximal loss in volume exceeded even 13%, which
is above the physiologically acceptable limit (6% ac-
cording to (Aubel and Thalmann, 2000)),
In this paper, we propose a new fast deformation
method for wrapping of muscles that overcomes this
problem as it can guarantee that changes in volume do
not exceed the given threshold. This method is based
on that described by (Huang et al., 2006) where vol-
ume preserving deformation is achieved by forming
a system of non-linear equations that is solved by an
iterative Gauss-Newton method with Lagrange mul-
tipliers. The main changes done to the original de-
scription were to adapt conditions and the computa-
tion process to our input data and goals. We also in-
troduced progressive steps in iterations to speed up
the convergence and parallelized the computation us-
ing OpenMP and, furthermore, investigated the possi-
bility to parallelize the computation using GPU.
The remainder of this paper is structured as fol-
lows. In the next section, we give a brief survey
of existing deformation methods that deal with vol-
ume preservation. Section 3 brings an overview of
our method; details are described in sections 4 and
5. Section 6 presents the experiments that were per-
formed. Section 7 concludes the paper and provides
an overview of possible future work.
2 RELATED WORK
Deformation methods can be divided into three main
categories: finite element methods (FEM), mesh-
skinning techniques and gradient domain deformation
techniques. FEM methods decompose the object to
be deformed into a set of interconnected nodes that
are scattered in the volume of the object (typically,
they form tetrahedral or hexahedral meshes) and as-
sociate each node with a strain tensor for modelling
local deformations at the node (Debunne et al., 2001).
Although these methods produce accurate results, es-
pecially, when large numbers of nodes are used, they
consume lot of memory and require substantial com-
putations, which renders them unsuitable for large-
scale real-time simulations.
Volume preserving mesh-skinning techniques
usually compute automatically a displacement field
that is used in the post-processing to shift vertices of
the surface mesh being deformed outward the skele-
ton of the object. Most of these method focus on pre-
serving volume locally (Botsch and Kobbelt, 2003),
(Rohmer et al., 2008). A global volume correction
technique is proposed by von Funck et al. (Von Funck
et al., 2008). The method, however, cannot preserve
shape of the mesh and avoid self-intersections. It is
important to highlight that calculation of correct dis-
placements requires that the skeleton lies inside the
volume defined by the surface, which is a condition
that is often violated in context of our application.
A good survey of gradient domain deformation
techniques is given in (Xu and Zhou, 2009). For a
surface mesh, these techniques define its energy as
a function that contains terms for detail and volume
preservation, position and other constraints. External
forces at vertices are also expressed as an energy func-
tion. A product of these two functions gives the defor-
mation energy function whose minimisation, which
is done by solving an over-constrained system of lin-
ear or non-linear equations, yield the new positions of
vertices in the deformed mesh (Huang et al., 2006),
(Zhou et al., 2005). We note that gradient domain de-
formation techniques are usually designed for direct
mesh editing, where only a small part of surface is
subject to external forces, which is again something
uncommon in our context.
FAST DEFORMATION FOR MODELLING OF MUSCULOSKELETAL SYSTEM
17

3 METHOD OVERVIEW
Our method is based on the gradient domain deforma-
tion technique described in (Huang et al., 2006). In
contrast to original description, however, it does not
assume that the mesh skeleton, whose change triggers
the deformation of surface mesh, is fully inside the
volume of the mesh. In our case, the skeleton is a
set of action lines representing the muscle (it is in-
herited from an action-line musculoskeletal model),
i.e., it is a set of independent poly-lines describing the
general path of muscle and being fixed to the underly-
ing moving bone (represented also as surface mesh).
As it can be seen in Figure 1, they typically do not
fully lie inside the muscle volume. Many of them
are just straight lines, so it was necessary to introduce
some reference point (we use the centroid of the bone
along which the muscle runs) to avoid unnatural rota-
tion of the deformed muscle. It is also typical that
poly-lines of the skeleton in its rest-pose (obtained
from MRI data) and in its current-pose (defined by
motion capture data) have nothing in common since
the coordinate space of the motion data used to fuse
the static rest-pose musculoskeletal model typically
differs from the coordinate space in which this model
was created. This is again something not considered
in the original technique since it was designed for in-
teractive animation. For more details, see our paper
(Kohout et al., 2011).
Figure 1: Sartorius, Rectus Femoris and Semitendinosus
muscles and their action lines (in similar colours).
With the triangular surface mesh of the muscle
in its rest-pose on input, the method starts with the
construction of a very low resolution of this surface,
which has only a few hundreds vertices but preserves
the basic shape of muscle. It can be done using
any decimation technique, however, it is preferable
if the new mesh is outer envelope of the original one.
Since muscles should be of simple shape, we use edge
collapse technique (Hoppe, 1999) available in VTK
toolkit (Schroeder et al., 2004) followed by an en-
largement of the produced mesh by a slight shifting
of the vertices in direction of their normals. Once the
coarse mesh is ready, the method uses mean value co-
ordinates interpolation (Ju et al., 2005) to express the
coordinates of the original mesh vertices as a combi-
nation of the control coarse mesh vertex coordinates.
We note that both the coarse mesh construction and
the computation of mean value coordinates can be
done (and it is done in our implementation) in the pre-
processing to speed up the deformation process.
A linear condition to preserve the shape of the
coarse mesh is formulated (details are given in Sec-
tion 4). A relative position of the coarse mesh to
the muscle skeleton in its rest-pose position is evalu-
ated (using mean value coordinates interpolation) and
a linear condition to preserve this position is formu-
lated. Naturally, both conditions hold for the Carte-
sian coordinates [x,s], where x are coordinates of ver-
tices of the coarse mesh and s coordinates of the rest-
pose poly-lines of the muscle skeleton. The deforma-
tion energy function, which is defined by these con-
ditions, is zero for these coordinates, i.e., f(x,s) = 0.
Conditions are, however, violated for [x,s
′
], where s
′
are coordinates of the vertices of current-pose poly-
lines, i.e., f(x,s
′
) > 0. The aim is to find new coordi-
nates x
′
of the coarse mesh vertices so that f(x
′
,s
′
) =
min, whilst the volume of the coarse mesh is pre-
served, i.e., g(x) = c = g(x
′
), where g(x) is a non-
linear function calculating the volume of the object
from its surface coordinates x.
The solution to this problem lies in solving an
over-constrained system of linear equations (it is de-
fined by the linear conditions) that is subject to the
non-linear volume constraint. The iterative Gauss-
Newton method with one Lagrange multiplier λ is
used for this purpose. As the coarse mesh contains
a few hundreds of vertices only, the numerical stabil-
ity of this method is good and, furthermore, it con-
verges quickly. When the speed of convergence drops
below the predefined threshold (or after some large
number of iterative steps), we switch the deforma-
tion process to the next stage. In this stage, in ev-
ery step of the Gauss-Newton method, the next value
of Lagrange multiplier λ is not calculated to preserve
the volume of the coarse mesh but to preserve the
volume of muscle mesh, which means that the de-
formed muscle mesh must be reconstructed from the
current coarse mesh (coordinates x
′
) using the pre-
computed mean value coordinates and the difference
in volume of the deformed and original muscle mesh
evaluated. The process stops when the difference is
below the given threshold (or alternatively after some
large number of iterations).
The overview of the method is in Figure 2.
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
18
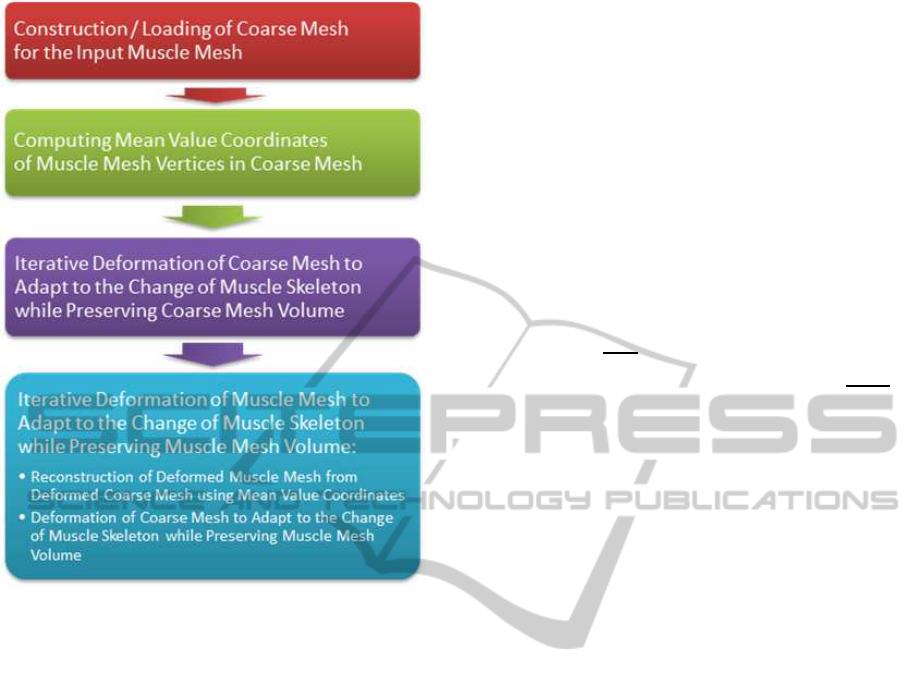
Figure 2: The schema of our deformation.
4 CONDITIONS
We can divide conditions into soft and hard condi-
tions. While the soft conditions, which are the condi-
tion of Laplacian to preserve the shape of the model to
be deformed and the condition of skeleton to initiate
the deformation process, might not be fulfilled, i.e.,
their error (deformation) energy might not be non-
zero after the deformation, the hard conditions must
be met. In our case, we would like to preserve the
original volume, so its value does not change.
4.1 Condition of Laplacian
Laplacian (Nealen et al., 2006) is a very common term
in computer graphic. It is used to describe a local
shape of mesh as a relation between each vertex x
i
and
its one-ring neighbours Ω, which is expressed as the
difference between the weighted mean of these neigh-
bours and the vertex, i.e., δ(x
i
) = (
∑
j∈Ω
w
i, j
· x
j
) − x
i
.
Using cotangent weights ω
j
, which are calculated
as cot|∠x
i
x
j+1
x
j
| + cot|∠x
i
x
j−1
x
j
|, ensures that the
shape of the mesh will be kept similar to the original
one as much as possible.
The formula for the Laplacian can be rewritten as
δ(x
i
) =
∑
N−1
j=0
w
i, j
· x
j
, where N is the number of ver-
tices. Weights w
i, j6=i
for not connected vertices x
i
and
x
j
are zero. The weight w
i, j=i
= −1. With this, the
set of equations for the Laplace condition can be eas-
ily formed as L · x = δ(x), where L is a sparse matrix
of weights w
i, j
for one vertex on each row, x is the
N × 3 matrix of Cartesian coordinates of vertices and
the matrix δ(x) on the opposite side of equation con-
tains Laplacian differential vertices.
The differential vertices are, however, not invari-
ant to the rotation of the mesh. Ignoring this fact, may
lead into flattening or unnatural rotation of the model.
We prevent this by rotating the differentials δ(x)
around axis ρ by angle φ computed in such a manner
that vector n =
u×v
|u×v|
after being rotated around this
axis ρ by angle φ is identical with vector n
′
=
u
′
×v
′
|u
′
×v
′
|
.
Vectors u,v are calculated as u = s
1
− s
0
,u
′
= s
′
1
− s
′
0
and v = r− s
0
,v
′
= r
′
− s
′
0
, where s
i
are vertices of the
muscle skeleton in its rest-pose position and s
′
i
are the
corresponding vertices of this skeleton in the current
pose position, r is the rest-pose reference point cho-
sen as the centroid of the bone along which the muscle
should wrap, whilst r
′
is the corresponding current-
pose reference point.
4.2 Condition of Skeleton
The condition of skeleton is used to preserve the rel-
ative position of the mesh and its skeleton. First, it
is necessary to match the poly-lines representing the
rest-pose and the current-pose paths of the skeleton
since these poly-lines may not be of the same length
or even may not have the same number of points.
The matching process (for detail, see (Kohout et al.,
2011)) exploits an arc-length parameterizationof both
poly-lines to successively introduce vertices from the
current-pose poly-line into the rest-pose one (and vice
versa), which is followed by subdividing long seg-
ments. By the end of this process, both poly-lines
will have the same number of points.
For each vertex s
i
of the rest-pose poly-line, its
mean value coordinates (MVC) k
i, j
in the mesh are
computed (Ju et al., 2005), so that s
i
=
∑
N−1
j=0
k
i, j
· x
j
.
With this, the set of equations for the condition of
skeleton can be easily formed as S · x = s
′
, where S
is a matrix of MVC coordinates k
i, j
for one skeleton
vertex on each row, x is the N × 3 matrix of Cartesian
coordinates of mesh vertices and the matrix s
′
on the
opposite side of equation contains Cartesian coordi-
nates of the current-pose poly-line vertices.
FAST DEFORMATION FOR MODELLING OF MUSCULOSKELETAL SYSTEM
19

4.3 Condition of Volume
Since we demand preserving the original volume as
precisely as possible, the condition of volume must
be formulated. It is simply defined as the non-linear
equation v(x)− c = 0, where v(x) is the function eval-
uating the volume of the mesh from its vertices x,
whilst c is the original volume of the mesh. The vol-
ume of the closed mesh can be evaluated in linear
time as a sum of oriented volumes of tetrahedrons de-
fined by each mesh triangle and some reference point,
e.g. (0,0,0). Hence, v(x) =
1
6
|
∑
N
t
−1
i=0
(x
i
1
× x
i
2
) · x
i
3
|,
where N
t
is the number of triangles in the mesh and
x
i
1
,x
i
2
,x
i
3
are coordinates of vertices of i-th triangle.
We note that the condition of volume is a hard con-
straint, i.e., it must be always fulfilled. This compli-
cates the solving process, indeed.
5 SOLVING
5.1 Iterative Algorithm Construction
We have now a set of linear conditions in form of
L
S
· x =
δ(x)
s
′
≡ A · x = d(x) (1)
where d(x) is a function of x because the differential
vertices δ(x) are not rotation invariant and, therefore,
depends on the Cartesian coordinates of x. However,
thanks to rotation of the differential vertices prior to
solution (see Section 4.1), the dependence of these
vertices on rotation is negligible, so we can approx-
imate this function by constant matrix d.
The obtained linear system is overdetermined, so
we have to use least squares method and solve
A
T
· A· x = A
T
· d ≡ L· x = b (2)
with the hard constraint for volume preservation:
g(x) = v(x) − c = 0 (3)
We will use an iterative approach as follows. We
define function f(x) as
f(x) ≡ L· x− b (4)
that we will minimise using Gauss-Newton numerical
method. Starting with an initial solution x
0
(the orig-
inal Cartesian coordinates of the mesh to deform in
our case), this method successively improves this so-
lution by adding an increment h
k
to it in every step,
i.e., x
k+1
= x
k
+ h
k
, where h
k
successively decreases
down to zero, i.e., for k → ∞, h
k
→ 0.
The change of f after every step h
k
added to x
k
can be described linearly using the first derivative as
f(x
k+1
) ≡ f(x
k
+ h
k
) ≈ f(x
k
) + J
f
(x
k
) · h
k
(5)
where J
f
(x
k
), or in shorter form J
f
, is Jacobi matrix
of f(x
k
). Now, we can derive the formula for h
k
:
f(x
k
+ h
k
) = 0
f(x
k
) + J
f
· h
k
= 0
f(x
k
) = −J
f
· h
k
J
f
T
· f(x
k
) = −J
f
T
· J
f
· h
k
(J
f
T
· J
f
)
−1
· J
f
T
· f(x
k
) = h
k
h
k
= (J
f
T
· J
f
)
−1
· J
f
T
· f(x
k
) (6)
Following the description in (Li, 1994), we add
volume loss compensation to every step, which yields
the new equation:
h
k
= −(J
f
T
· J
f
)
−1
· (J
f
T
· f(x
k
) + J
g
T
· λ
k
) (7)
where J
g
is Jacobi matrix of g(x
k
) and λ
k
is the La-
grange coefficient. The matrix J
g
, which is composed
from partial derivatives of the volume function v(x
k
),
describes the directions of volume growth, whilst the
coefficient λ
k
describes its amount.
The Lagrange coefficient λ
k
must be chosen to
both fix the overall volume loss which has already oc-
curred (in previous steps) and to compensate the vol-
ume change which will be caused by adding h
k
from
eq. 6 to the mesh in the current step. This means
that λ
k
depends on the volume function g(x
k
) and the
volume change h
k
· J
g
(when h
k
→ 0), i.e.,
λ
k
= R
k
· (g(x
k
) + J
g
· (J
f
T
· J
f
)
−1
· J
T
f
· f(x
k
)) (8)
where R
k
, which compensates (J
f
T
· J
f
)
−1
from eq. 7
and normalises J
g
, is calculated as
R
k
= (J
g
· (J
f
T
· J
f
)
−1
· J
g
T
)
−1
(9)
If |h
k
| is smaller than the given ε (or after some
sufficient large amount of steps), the deformation pro-
cess stops yielding the Cartesian coordinates x
′
of the
deformed mesh in x
k
.
5.2 Improvements of the Algorithm
Huang et al. (Huang et al., 2006) suggested changing
the length of step h
k
by multiplying it by some param-
eter α, whose values ranges from 0 to 1, to improve
the stability of the process. Hence, the deformation
formula changes to
x
k+1
= x
k
+ α· h
k
x
′
= x
n
⇔ h → ε
(10)
We have found experimentally that instead of using a
constant value for this parameter, it is better to itera-
tively decrease the α value (starting from value 0.5)
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
20

Table 1: Dependence of the number of iterations and the
volume preservation ratio on the α values.
α Num. of Iterations Vol. preservation
0.025 186 99.89%
0.050 106 99.85%
0.100 59 99.77%
0.250 27 99.58%
0.500 24 99.35%
0.750 76 99.19%
adaptive 57 99.93%
while getting closer to the final solution. This leads
to a faster convergence at the beginning and a more
precise solution at the end – see Table 1.
However, when we shorten the step, we shorten
also the compensation of the cumulativevolume error.
This is an undesired effect, so we have to divide the
amount of volume compensation in the step h
k
by α
k
,
which will disable the effect of α
k
multiplication in
later steps and allow all the volume error to be fixed.
Another issue is that processing of large meshes
would be not only time and memory consuming but
also numerically unstable. Hence, as described in sec-
tion 3, instead of using the original mesh, the iterative
method works with its coarse version; the coordinates
of the original mesh can be obtained from the current
coarse mesh x
k
by MVC coordinatesinterpolation. As
a consequence of this, to preserve the volume of the
original mesh in the deformation, the volume func-
tion v (see eq. 3) must be evaluated for the original
high detail mesh. In practise, however, we do not need
to evaluate the volume so precisely at the beginning,
which means that we can use the coarse mesh for the
volume evaluation as well and only after getting close
to the solution, we switch to the original mesh. As the
coarse mesh has larger volume than the original one
(this is caused by the fact that the coarse mesh is an
external envelope of the original mesh), which means
that absolute size of volume error will be higher,when
using the coarse mesh for the calculation of volume,
the evaluated volume must be divided by the ratio of
original volumes of those two meshes. The final set
of solution equations then is:
x
k+1
= x
k
+ α
k
· h
k
h
k
= −(J
f
T
· J
f
)
−1
· (J
f
T
· f(x
k
) + J
g
T
· λ
k
)
λ
k
= R
k
· (dv(x
k
)/α
k
+ J
g
· (J
f
T
· J
f
)
−1
· J
T
f
· f(x
k
))
R
k
= (J
g
· (J
f
T
· J
f
)
−1
· J
g
T
)
−1
dv(x
k
) = {
g(x
k
) ·
g(x
0
)
g( ˜x
0
)
; if h
k
> ε
g( ˜x
k
); if h
k
→ ε
(11)
where x
k
is the matrix of the coarse mesh vertices and
˜x
k
is the matrix of the original mesh vertices.
5.3 Evaluation of Equations
Although all the relations have been formed, it may
still not be clear how to use them.
Matrix A from eq. 1 is composed from the Lapla-
cian and skeleton matrices (see section 4. These ma-
trices were built considering x to be N × 3 matrix
with all three single vertex coordinates on one row,
where N denotes the number of mesh vertices. With
this, the matrix L = A
T
· A is N × N, which is an im-
portant memory reduction in comparison to obvious
3· N × 3 · N (we have N conditions for x-coordinate,
N for y-coordinate and N for z-coordinate).
Matrix d ≈ d(X) has the same width as x and the
same height as A, i.e., b = A
T
·d is a matrix N ×3. Ja-
cobi matrix J
f
(x) of f(x) = L· x− b is the first deriva-
tive of linear function. Hence,
J
f
(x) = L (12)
and the size of J
f
(x) is N × N.
The volume error function g(x) from eq. 3 is a
scalar function of N × 3 mesh coordinates. Jacobi
matrix of J
g
(x) is a row vector 1 × 3 · N of partial
derivatives of g(x) with respect to each coordinate, so
J
g
(x) = (
δg(x)
δx
0
x
;
δg(x)
δx
0
y
;
δg(x)
δx
0
z
;
δg(X)
δx
1
x
;
δg(x)
δx
1
y
;
δg(x)
δx
1
z
;···). This
can be done analytically:
δg(x)
δx
i
=
1
6
N
i
∑
j=1
(x
j
1
× x
j
2
) (13)
where N
i
is the number of triangles sharing the vertex
x
i
and x
j
1
or x
j
1
are the other vertices of j-th triangle.
Because of compression used for L and x, the sizes
of matrices that must be multiplied to get λ
k
and h
k
(see eq. 11) are incompatible. Hence, it is neces-
sary either to expand matrices L and J
f
to 3· N × 3· N
form or to use a little tricky manipulations with rows
and columns of operands as follows. First, we trans-
form J
g
T
from a vector to N × 3 matrix such that
partial derivatives of the same mesh vertex are on a
single row of the matrix. This allows us to multiply
(J
f
T
J
f
)
−1
J
g
T
. Now, we must transform the result ma-
trix back into a vector. The dot product of J
g
and this
vector gives as a scalar value whose reciprocal is R
k
.
A similar solution is used for the right part of formula
for λ
k
(eq. 11) and in evaluation of formula for h
k
.
The simplified version of the algorithm in C is:
change = DOUBLE_MAX;
alpha = 0.1;
X[0] = orig;
i = 0;
while (change > epsilon) {
g = calculateVolumeError(orig, X[i]);
Jg = calculateJg(X[i]); // eq. 13
lambda = .. //eq. 11, Jf = L
FAST DEFORMATION FOR MODELLING OF MUSCULOSKELETAL SYSTEM
21

h = ... //eq. 11
X[i+1] = X[i] + alpha * h;
change = |X[i+1]-X[i]|
if (change < thrs) {
//we are getting close to the solution
change = decreaseAlpha();
}
i++;
}
return X[i+1];
6 EXPERIMENTS AND RESULTS
Our approach was implemented in C++ (MS Visual
Studio 2010) under the Multimod Application Frame-
work – MAF (Viceconti et al., 2004), which is a vi-
sualisation system based mainly on VTK (Schroeder
et al., 2004) and other specialised libraries. This
framework is designed to support the rapid develop-
ment of biomedical software. It is particularly useful
in multimodal visualisation applications, which sup-
port the fusion of data from multiple sources and in
which different views of the same data are synchro-
nised, so that when the position of an object changes
in one view, it is updated in all the other views. Our
implementation was then integrated into the Muscle-
Wrapping software
1
that is being developed within
the VPHOP project (VPHOP, 2010). Experiments
were conducted on various real data sets of muscles
with typical sizes about 15K vertices on Intel Core
i7 2.67 GHz, 12 GB DDR3 1.3GHz RAM and Intel
Core i7 4.4 Ghz, 16 GB DDR3 1.6GHz RAM, both
with Windows 7 Pro x64.
Figure 3 shows the deformation of muscles of
right thigh at current-pose frames t = 0.00, 0.25, 0.50
and 0.75 of the 1.56 seconds long walk sequence.
The deformation process of a single muscle con-
sumed 250–650 ms per frame on Intel Core i7 2.67
GHz computer, which makes the new method to be
about 8–20 times slower than our former deforma-
tion method that was based on the mesh skinning with
volume correction in post-processing (Kohout et al.,
2011). Nonetheless, the proposed method is still fast
enough for our purpose since the deformation of all
these muscles required a few seconds. We note that
this time does not include the time consumed in the
pre-processing to compute the coarse mesh and to es-
tablish the relationship between the both meshes (our
implementation takes up to one minute depending on
the model complexity).
1
http://graphics.zcu.cz/Projects/Muskuloskeletal-
Modeling
Figure 3: Wrapping of the muscles of right thigh during the
movement.
The shapes of the deformed and rigidly trans-
formed sartorius muscle are compared in Figure 4.
While the rigid transformation does not preserve the
attachment of the muscle to the bones and provides
the user with an unnatural result, the deformation pro-
duces a plausible result. The loss in the volume of the
muscle was about 0.02%, which is much lower than
the loss 11% observable in our former method.
Figure 4: Sartorius muscle with its action line (yellow) in
the rest-pose position (above) and at frame t = 0.00 of the
walk sequence (below), transformed rigidly (blue) and de-
formed (green) according to the change of its action line.
As it can be seen in Figure 5, the new method pre-
serves the volume much better also for other muscles
and other poses. Nevertheless, for some poses, the
maximal change in the volume of muscle may ex-
ceed 6%, which is, according to (Aubel and Thal-
mann, 2000)), the physiologically acceptable limit.
The reason for such a poor result is that the iterative
process terminated for semitendinosus muscle not be-
cause the optimal solution had been reached but be-
cause the maximal allowed number of iterations (100
in our case) had been performed. For all other mus-
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
22
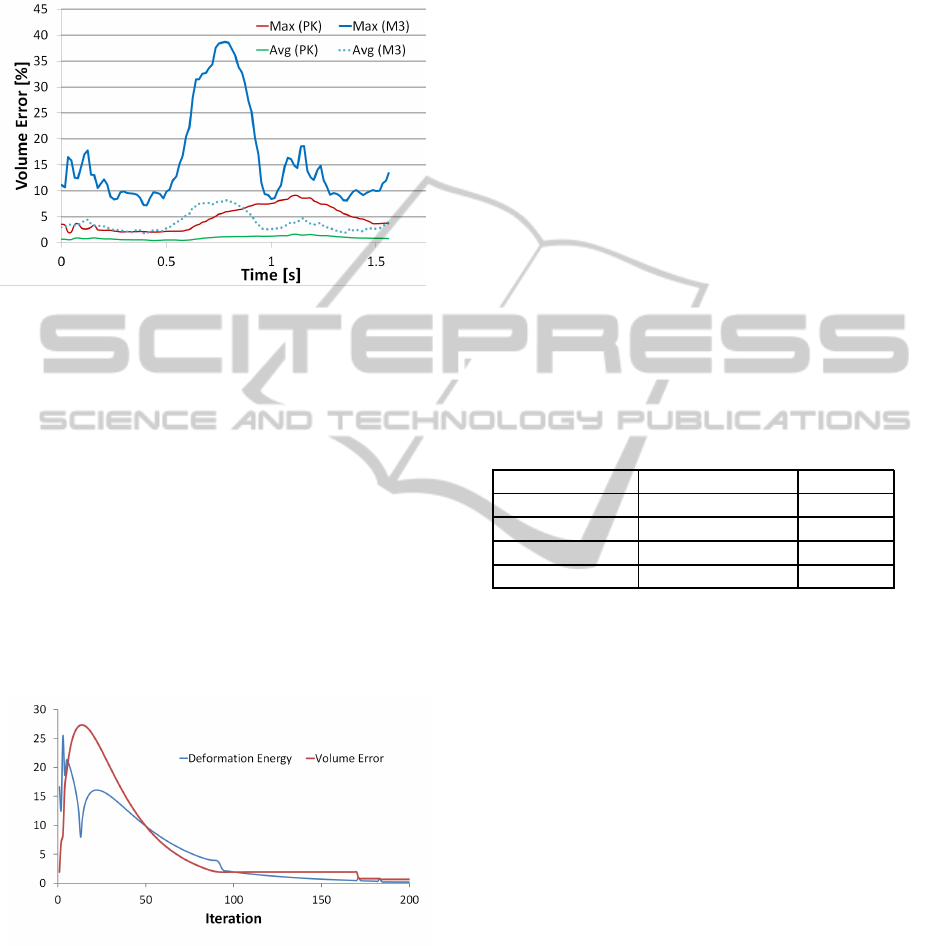
cles, the maximal volume error is within the physio-
logically acceptable limits.
Figure 5: Comparison of maximal and average volume er-
rors for muscles of the right thigh in the walk sequence for
our former method (M3) and the proposed one (PK).
The results can be easily improved by increas-
ing the maximal allowed number of iterations as it
is demonstrated in Figure 6 that shows the depen-
dence of the deformation energy and volume error
on the number of iterations for semitendinosus mus-
cle. More than 170 iterations were needed before
the deformation energy dropped to the level when the
method could start using the detailed mesh for the vol-
ume computation – see the abrupt change in the vol-
ume error function. Whilst the volume error was al-
most 10% after 100 iterations (see Figure 5), the final
volume error (after 200 iterations) is about 0.04%.
Figure 6: Monotonic functions of the deformation energy
and the volume error in the dependence on the number of
iterations.
There are two main factors contributing to such
a slow convergence of the method. First, it has
been found that many tested muscles (semitendinosus
muscle included), extracted from MRI images during
our previous EU-funded project (LHDL, IST-2004-
026932) as described in (Testi et al., 2010), are not
closed manifolds. This causes troubles when creat-
ing the coarse mesh and expressing the relations be-
tween both meshes, which lead into an appearance of
ill-shaped triangles in the coarse mesh, and, if non-
manifold edges are present at a very narrow place
(typically, tendon part), also into having more than
just one component of the coarse mesh. As a re-
sult, the method needs more iterations and, further-
more, strange spikes on the deformed mesh may ap-
pear. This could be solved by refining the muscles,
however, this is a part of our future work.
Next, for some muscles (e.g., sartorius), there is
only a loose relation between the muscle surface and
its skeleton, which negatively influences the number
of iterations required. This is demonstrated in Table 2
that shows the processing time needed for various
– already refined – muscles of different sizes. Vas-
tus lateralis, which contains more than 50K triangles
but have skeleton going through its volume, was de-
formed faster than sartorius, which has less than 10K
triangles but its skeleton lies outside the mesh.
Table 2: Performance of our method on Intel Core i7 2.67
GHz, 12 GB DDR3 1.3GHz RAM.
Muscle Num. of Triangles Time [ms]
Rectus femoris 5238 268
Sartorius 9908 476
Adductor longus 13912 550
Vastus lateralis 50240 379
To reduce the required processing time, we par-
allelized routines for the multiplication of matrices,
the calculation of MVC coordinates of the muscle
mesh in the coarse mesh and the reconstruction of the
muscle mesh from the coarse one using OpenMP, a
multiplatform interface for parallel programming in
C, C++ and Fortran described, e.g., in (Gatlin and
Isensee, 2010). OpenMP allows automatic assign-
ment of independent iterations of a for cycle to work-
ing threads, providing that the cycle is prefixed in the
code by special directives as it is shown in Figure 7.
Table 3 shows the results of the parallelization.
The optimal performance obviously is achieved when
the number of threads to be used for the calculation
equals the number of physical cores of CPU. As it
can be seen, speed-up of at least 40% can be reached
on commodity hardware.
We have investigated also an option of speeding
up multiplication of matrices by employing GPU us-
ing CUBLAS library, which is a standard part of
CUDA system (nVidia, 2011). Providing that matri-
ces to be multiplied are represented by one dimen-
sional arrays, the speed-up on a system with NVIDIA
GeForce 9600 GT 512 MB is about 978, otherwise,
FAST DEFORMATION FOR MODELLING OF MUSCULOSKELETAL SYSTEM
23

Figure 7: Parallelization of the multiplication of matrices A
and B by OpenMP directives).
Table 3: Time needed by parallel version for processing a
mesh of 6978 vertices on Intel Core i7 4.4 Ghz.
Threads Time [ms] Speed-up
1 397 –
2 278 1.43
4 248 1.60
8 262 1.51
16 295 1.35
which is our case, it is only 2.26 because of the re-
quired transformation from the internal data structure
into the array and vice versa. Still this is an important
speed-up.
7 CONCLUSIONS
In this paper we described a gradient domain volume
preserving deformation method suitable for muscle
wrapping application. The deformation is governed
by the change of the action line (skeleton) of the mus-
cle mesh - the method iteratively alters the positions
of mesh vertices to adapt the change of the skele-
ton whilst preserving the volume. For any of tested
muscles, 200 iterations are enough to achieve vol-
ume error below 0.04%, 100 iterations are sufficient
for any manifold muscles. The sequential process-
ing of typical mesh requires about 400 ms on com-
modity hardware. When parallelized using OpenMP
the required time may drop to 250 ms depending on
hardware configuration and even to a couple of ms
(estimated) when parallelized using CUDA. Hence,
the method is fast enough to be used for the mus-
cle wrapping for clinical practise. An understandable
drawback of the approach is its sensitivity to the mesh
quality. For non-manifold meshes, which often result
from marching cube iso-surface extraction, the con-
vergence of the method may be very slow or even the
method may produce a mesh having some parts un-
naturally deformed (e.g., spikes appearance, strange
twists). Some mesh filtering prior to the deformation
is, therefore, typically needed. This filtering is a part
of our future work as well as proper validation of our
method in clinical context.
ACKNOWLEDGEMENTS
This work was supported by the Information Soci-
ety Technologies Programme of the European Com-
mission under the project VPHOP (FP7-ICT-223865).
The authors would like to thank the various people
who contributed to the realisation of the MAF and
LHPBuilder software and to various people who pro-
vided condition under which the work could be done.
REFERENCES
AnyBody (2010). Anybody technology,
http://www.anybodytech.com.
Arnold, A. S., Salinas, S., Asakawa, D. J., and Delp, S. L.
(2000). Accuracy of muscle moment arms estimated
from mri-based musculoskeletal models of the lower
extremity. Computer aided surgery official journal of
the International Society for Computer Aided Surgery,
5(2):108–119.
Aubel, A. and Thalmann, D. (2000). Efficient muscle shape
deformation. In IFIP, pages 132–142.
Audenaert, A. and Audenaert, E. (2008). Global opti-
mization method for combined spherical-cylindrical
wrapping in musculoskeletal upper limb modelling.
Computer Methods and Programs in Biomedicine,
92(1):8–19.
Blanco, F. R. and Oliveira, M. M. (2008). Instant mesh de-
formation. Proceedings of the 2008 symposium on In-
teractive 3D graphics and games SI3D 08, 1(212):71–
78.
Blemker, S. S. and Delp, S. L. (2005). Three-dimensional
representation of complex muscle architectures and
geometries. Annals of Biomedical Engineering,
33(5):661–673.
Botsch, M. and Kobbelt, L. (2003). Multiresolution surface
representation based on displacement volumes. Com-
puter Graphics Forum, 22(3):483–491.
Debunne, G., Desbrun, M., Cani, M.-P., and Barr, A. H.
(2001). Dynamic real-time deformations using space
& time adaptive sampling. In Proceedings of the 28th
annual conference on Computer graphics and interac-
tive techniques, SIGGRAPH ’01, pages 31–36, New
York, NY, USA. ACM.
Delp, S. L. and Loan, J. P. (2000). A computational frame-
work for simulating and analyzing human and animal
movement. Computing in Science and Engineering,
2(5):46–55.
Erdemir, A., McLean, S., Herzog, W., and Van Den Bogert,
A. J. (2007). Model-based estimation of muscle forces
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
24

exerted during movements. Clinical Biomechanics,
22(2):131–154.
Favre, P., Gerber, C., and Snedeker, J. G. (2010). Auto-
mated muscle wrapping using finite element contact
detection. Journal of Biomechanics, 43(10):1931–
1940.
Gao, F., Damsgaard, M., Rasmussen, J., and Christensen,
S. T. (2002). Computational method for muscle-path
representation in musculoskeletal models. Biological
Cybernetics, 87(3):199–210.
Garner, B. and Pandy, M. (2000). The obstacle-set method
for representing muscle paths in musculoskeletal
models. Computer Methods in Biomechanics and
Biomedical Engineering, 3(1):1–30.
Gatlin, K. S. and Isensee, P. (2010). Reap
the benefits of multithreading without all
the work. http://msdn.microsoft.com/en-
us/magazine/cc163717.aspx.
Hoppe, H. (1999). New quadric metric for simplifying
meshes with appearance attributes. Proc IEEE Con-
ference on Visualization VIS99, pages 59–66.
Huang, J., Shi, X., Liu, X., Zhou, K., Wei, L.-Y., Teng,
S.-H., Bao, H., Guo, B., and Shum, H.-Y. (2006).
Subspace gradient domain mesh deformation. ACM
Transactions on Graphics, 25(3):1126–1134.
Jensen, R. and Davy, D. (1975). An investigation of muscle
lines of action about the hip: A centroid line approach
vs the straight line approach. Journal of Biomechan-
ics, 8(2):103–110.
Ju, T., Schaefer, S., and Warren, J. (2005). Mean value
coordinates for closed triangular meshes. ACM Trans-
actions on Graphics, 24(3):561–566.
Kohout, J., Clapworthy, G. J., Martelli, S., Wei, H., Vice-
conti, M., and Agrawal, A. (2011). Fast muscle wrap-
ping. Computers & Graphics. Submitted for publica-
tion.
Li, S. Z. (1994). Markov random field models in com-
puter vision. In Eklundh, J.-O., editor, ECCV (2), vol-
ume 801 of Lecture Notes in Computer Science, pages
361–370. Springer.
Marsden, S. P. and Swailes, D. C. (2008). A novel approach
to the prediction of musculotendon paths. Proceed-
ings of the Institution of Mechanical Engineers Part H
Journal of engineering in medicine, 222(1):51–61.
Nealen, A., Igarashi, T., Sorkine, O., and Alexa, M. (2006).
Laplacian mesh optimization. In Proceedings of the
4th international conference on Computer graphics
and interactive techniques in Australasia and South-
east Asia, GRAPHITE ’06, pages 381–389, New
York, NY, USA. ACM.
nVidia (2011). Cuda zone. http://developer.nvidia.com/ca
tegory/zone/cuda-zone.
OpenSim (2010). Opensim project, https://simtk.org/home
/opensim.
Rohmer, D., Hahmann, S., and Cani, M.-P. (2008). Lo-
cal volume preservation for skinned characters. Com-
puter, 27(7):1919–1927.
Schroeder, W., Martin, K., and Lorensen, B. (2004). The
Visualization Toolkit, Third Edition. Kitware Inc.
Testi, D., Quadrani, P., and Viceconti, M. (2010). Phys-
iomespace: digital library service for biomedical
data. Philos Transact A Math Phys Eng Sci,
368(1921):2853–2861.
van der Helm, F. and Veenbaas, R. (1991). Modelling the
mechanical effect of muscles with large attachment
sites: Application to the shoulder mechanism. Journal
of Biomechanics, 24(12):1151–1163.
Viceconti, M., Astolfi, L., Leardini, A., Imboden, S.,
Petrone, M., Quadrani, P., Taddei, F., Testi, D., and
Zannoni, C. (2004). The multimod application frame-
work. Information Visualisation, International Con-
ference on, 0:15–20.
Von Funck, W., Theisel, H., and Seidel, H. P. (2008).
Volume-preserving mesh skinning. In Vision Model-
ing and Visualization, pages 409–414. IOS Press.
VPHOP (2010). the osteoporotic virtual physiological hu-
man, http://vphop.eu.
Xu, W.-W. and Zhou, K. (2009). Gradient domain mesh
deformation a survey. Journal of Computer Science
and Technology, 24(1):6–18.
Zhou, K., Huang, J., Snyder, J., Liu, X., Bao, H., Guo, B.,
and Shum, H.-Y. (2005). Large mesh deformation us-
ing the volumetric graph laplacian. ACM SIGGRAPH
2005 Papers on SIGGRAPH 05, 1(212):496.
FAST DEFORMATION FOR MODELLING OF MUSCULOSKELETAL SYSTEM
25
