DENSE PIXEL MATCHING BETWEEN UNRECTIFIED AND

DISTORTED IMAGES USING DYNAMIC PROGRAMMING

Jerome Thevenon, Jesus Martinez-del-Rincon, Romain Dieny and Jean-Christophe Nebel

Digital Imaging Research Centre, Kingston University, Penhryn Road, Kingston-Upon-Thames, KT1 2EE, Surrey, U.K.

Keywords: Stereo Correspondence, Dynamic Programming, Unrectified Images, Distorted Images.

Abstract: In this paper, a novel framework for dense pixel matching based on dynamic programming is introduced.

Unlike most techniques proposed in the literature, our approach assumes neither known camera geometry

nor the availability of rectified images. Under such conditions, the matching task cannot be reduced to

finding correspondences between a pair of scanlines. We propose to extend existing dynamic programming

methodologies to a larger dimensional space by using a 3D scoring matrix so that correspondences between

a line and a whole image can be calculated. After assessing our framework on a standard evaluation dataset

of rectified stereo images, experiments are conducted on unrectified and non-linearly distorted images.

Results validate our new approach and reveal the versatility of our algorithm.

1 INTRODUCTION

Dense pixel matching is a low-level process which is

involved in many computer vision applications

including navigation, security, entertainment and

video surveillance. Not only is it often an essential

step in 3D reconstruction from a pair of stereo

images, but it is also used in object detection and

video tracking, especially when the camera is not

fixed (Note, et al., 2006); (Yaguchi,, et al., 2009) as

it is the case with camera phones (Yin, et al., 2007).

Recent reviews describe and analyse the many

algorithms which have been proposed to address this

matching process (Scharstein and Szeliski, 2002),

(Lazaros, et al., 2008). Most approaches performing

dense pixel matching assume images have been

rectified so that their task can be reduced to finding

correspondences between a pair of scanlines. Among

these techniques, those based on dynamic

programming (DP) are of particular interest since

they combine good accuracy with low computational

complexity as demonstrated by a recent real-time

FPGA hardware implementation (MacLean, et al.,

2010). Their main drawback is that they require the

knowledge to project images onto a common

coordinate system. Although, in many applications

those transformations can be estimated by either

camera calibration or image rectification, calibration

is sometimes either impossible or impractical,

whereas the computational cost of accurate

rectification models prohibits their usage in real-

time application. Moreover, none of these methods

is suitable when a camera lens displays unexpected

distortions, such as those generated by raindrops,

weatherproof covers or dust.

In this paper, we propose a novel DP-based

dense pixel matching algorithm which can handle

unrectified and non-linearly distorted images. After

a state-of-the-art review, we detail our novel

matching algorithm. Finally, it is validated with

experiments conducted on unrectified images and

images displaying significant deformations.

1.1 Related Work

Generally, pixel matching approaches (Barnard, et

al., 1982); (Dhond, et al., 1989), (Brown, et al.,

1992); (Jones, et al., 1997); (Scharstein and Szeliski,

2002) assume that images have been rectified so that

the task is simplified to establishing

correspondences between corresponding rows of the

rectified images. The standard process for

rectification is homography based, also called planar

rectification, where image planes are transformed so

that the corresponding space planes coincide

(Ayache and Hansen, 1998); (Hartley, 1999). A

major limitation of this class of approaches is that, if

epipoles are located in the images, planar

rectification produces infinitely large images. This

problem has now been solved under specific

216

Thevenon J., Martinez-del-Rincon J., Dieny R. and Nebel J..

DENSE PIXEL MATCHING BETWEEN UNRECTIFIED AND DISTORTED IMAGES USING DYNAMIC PROGRAMMING.

DOI: 10.5220/0003812602160224

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 216-224

ISBN: 978-989-8565-04-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

conditions by using either cylindrical (Roy, et al.,

1997) or spherical rectifications (Pollefeys, et al.,

1999); (Wan and Zhou, 2008). In addition to adding

significant computational complexity, these methods

still overlook issues such as sub pixel coordinates,

infinite epipoles (Lim, et al., 2004) and the non

preservation of conjugate epipolar polarities (Oram,

2001). An alternative to these approaches is to fully

calibrate cameras to estimate the appropriate

transformation between images. However, since this

process is usually manual or relies on very specific

environments, its usage has very strong limitations.

In any case, all these methods depend on finding a

set of accurate matching points, resampling images

and appropriate lens distortion models, of all which

affect the matching performance. Moreover, there

are scenarios where these methods are totally

inadequate. For example, visual tracking is seriously

degraded by weather conditions when the presence

of water drops produces undesirable temporal and

localised distortions (Barnum, et al., 2007); (Garg

and Nayar, 2004); similarly, vision systems on space

exploration rovers are affected by dust accumulation

(Willson, et al., 2005).

Although performing dense pixel matching

without prior image transformation is an attractive

proposition, very few algorithms have been

suggested. This problem was addressed using either

multi-resolution image correlation (Duchaineau, et

al., 2007); (Zhengping, 1988) or a genetic algorithm

(Tippetts, et al., 2010). It was also suggested that a

self-organizing neural network could potentially be

used under these conditions (Vanetti, et al., 2009).

Unfortunately, all these methods display high

computational complexity and recursivity, which

makes them unsuitable for real-time and hardware

implementations.

This review highlights the limitations of

rectification and calibration procedures and shows

that, currently, bypassing this step leads to solutions

with high computation costs. In order to address this,

a novel algorithm could be designed by extending

one of the approaches developed to tackle in real-

time the simpler task of scanline matching

(Forstmann, et al., 2004); (Gong, et al., 2006), (Lu,

et al., 2009); (Salmen, et al., 2009); (Wang, et al.,

2006); (Yang, et al., 2006). Among them, techniques

based on DP seem particularly suitable: although

they are not the most accurate, performance analysis

has shown they provide an excellent compromise

between accuracy and speed (Cox, et al., 1996);

(MacLean, et al., 2010); (Scharstein and Szeliski,

2002); (Brown, et al., 2003); (Tappen and Freeman,

2003). Their low intrinsic computational complexity

even led to a recent FPGA hardware implementation

(MacLean, et al., 2010).

In this paper, we propose a novel dense pixel

matching algorithm based on the DP paradigm

which can operate with unrectified images without

camera calibration.

2 ALGORITHM

We propose a novel dynamic programming

algorithm which is able to establish dense pixel

correspondences between two unrectified and/or

distorted images. Since our method is based on a DP

approach, it relies on two main steps: the storage of

local calculations and their reuse to produce a global

solution. In this section, we first describe how a 3D

scoring matrix is computed. Then, we propose a

refinement of these calculations, i.e. introduction of

the extended gap concept. Finally, we detail the

backtracking phase which allows generating optimal

global correspondences.

It is important to note that, although the usage of

3D matrices within DP based pixel matching

algorithms was proposed by Sun (Sun, 2002); (Sun-

2, 2002), this was only a means of efficiently

calculate the correlations over a sliding window.

This did not address the requirement of image

rectification and was only suitable for scanline

matching.

2.1 3D Scoring Matrix

Similarly to many dynamic programming-based

algorithms designed for scanline matching (Geiger,

et al., 1992); (Belhumeur, 1996); (Cox, et al., 1996);

(Torr and Criminisi, 2004), the first stage of our

algorithm fills in a scoring matrix according to a

given scoring scheme. However, our approach does

not restrict itself to finding pixel correspondences

between scanlines, but between a scanline and an

entire image. The strength of this scheme is that

images do not need to be rectified and matching can

be achieved even when one of the images displays

important distortions. Consequently, a scanline on

the first image does not need to match a straight line,

but may correspond to a curve in the second image

(see Figure 1). Since this algorithm is an extension

of an algorithm designed for matching stereo pairs

of images (Authors, 1111), we use the same

convention: the first and second images are referred

as the left and right images.

First, a 3D scoring matrix is generated for each

scanline s of the left image. Assuming the left image

DENSE PIXEL MATCHING BETWEEN UNRECTIFIED AND DISTORTED IMAGES USING DYNAMIC

PROGRAMMING

217

a) b)

Figure 1: Views of the same scene captured using different

camera lenses. Green curves: groundtruth correspondence

between 3 scanlines of image a) and pixels of image b).

scanlines have a length L and the dimensions of the

right image are WxH (width x height), the size of the

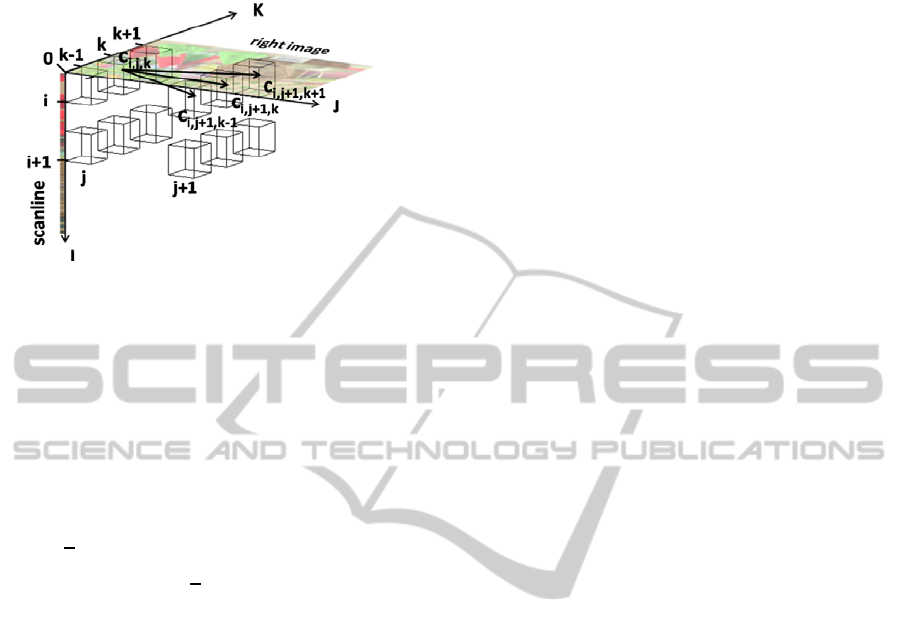
scoring matrix, sc, is LxWxH. A matrix cell c

i,j,k is

defined by three coordinates, where i represents the

elements of the scanline and j and k the column and

line of the right image (see Figure 2).

Figure 2: 3D scoring matrix.

Matrix cells store the maximum value which can

be achieved by extending a previous alignment.

When a DP approach is used to find

correspondences between two scanlines, an

alignment can only be extended in three manners:

pixels of the left and right images may have similar

values, i.e. there is a match, or one of the pixels may

be occluded in either the first or the second

sequence, i.e. a gap has to be introduced. Here, an

alignment finishing in the cell, c

i,j,k, can be extended

in seven ways.

Since a match means that a pixel of the scanline

corresponds to a pixel in the image, the matching

cell must be contiguous to the previous cell, c

i,j,k.

Moreover, dynamic programming approach requests

moving forward in order to come to an end.

Consequently, a match can occur in either cell

i+1,j+1,k, ci+1,j+1,k+1 or ci+1,j+1,k-1, which corresponds to

a correspondence between the next pixel in the

scanline (i+1), and respectively, the next pixel in the

next column (j+1) in the same line (k), match m

1, the

line below (k+1), match m2, or the line above (k-1),

match m

3 (see Figure 3).

Since a change of line and column means

moving by a distance of

√

pixels in the image, this

implicitly adds a virtual gap of 

√

−1pixels.

Therefore, this type of match should be less

rewarded than a match along the i+1,j+1,k direction.

If matches between pixels cannot be found, a gap

has to be introduced in either the image or the

scanline. A gap in the image indicates that a scanline

pixel does not have any correspondence in the

image: this pixel is occluded in the right image.

Consequently, the alignment is extended by moving

to the next element in the scanline, i.e. c

i+1,j,k (gap

g4) (see Figure 4).

Figure 3: Matching.

Figure 4: Gap in the image.

Alternatively, image pixels may be occluded in

the left image. This implies not moving in the I

direction, i.e. the displacement in the matrix is

towards either c

i,j+1,k (gap g1), ci,j+1,k+1 (gap g2) or

i,j+1,k-1 (gap g3) (see Figure 5). Similarly to the case

of matching, a change of line implies adding an

extra gap of 

√

−1pixels, which also needs to be

penalised.

As shown, each cell of the 3D scoring matrix can

be accessed from 7 directions. During the filling

process, for each of these directions the cell value is

calculated according to the cost of the move, i.e.

match or gap costs: the highest value and the

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

218

direction(s) it is coming from are stored in the cell.

This information is used in the backtracking process.

Figure 5: Gap in the scanline.

In order to define the costs of these possible

moves, we introduce 3 parameters: m is the reward

for a perfect match, g is the penalty for a single gap,

and Δ is the penalty for an imperfect match, which is

set at the absolute value of the intensity difference

between the scanline pixel, s(i), and the image pixel,

Im(j,k).

Δ=

() − (,)

(1)

Using these parameters, the cost of adding an extra

gap of 

√

−1pixels, p, can be expressed by:

=

√

−1(−) (2)

Before starting the filling process, the matrix

needs to be initialised. First, the initial alignment

score is set to zero. This involves extending the

initial matrix of dimensions LxWxH with the planes

(0,J,K) and (I,0,K). Since the alignment can start

from any line of the image, cells with coordinates

i=0 and j=0 are filled with zeros. Then other cells

from the planes (0,J,K) and (I,0,K) are initialised

according to cumulated gap penalties.

Finally, the scoring matrix, sc, is filled in

according to the following pseudo-code:

for i=1 to L

for j=1 to W

for k=1 to H

Δ ← |s(i)-Im(j,k)|

m1 ← sc(i-1,j-1,k)+m-

Δ

m2 ← sc(i-1,j-1,k+1)+m-Δ-p

m3 ← sc(i-1,j-1,k-1)+m-Δ-p

g1 ← sc(i,j-1,k)+m-g

g2 ← sc(i,j-1,k+1)+m-g-p

g3 ← sc(i,j-1,k-1)+m-g-p

g4 ← sc(i-1,j,k)+m-g

sc(i,j,k) ← max(m1,m2,m3,g1,g2,g3,

g4)

end for

As a consequence, the time complexity of the

proposed algorithm is 

(



)

per scanline.

2.2 Extended Gap

In the initial scoring scheme, each individual gap has

a fixed penalty. However, due to the nature of stereo

images and successive video frames where different

perspectives create partial object occlusions,

occluded pixels tend to cluster instead of being

equally distributed across an image. We propose to

exploit this observation by introducing a lower

penalty for new gaps which extend existing gaps. An

affine gap penalty is used where the initial gap

opening penalty is set at g and each extension of a

gap increases the total penalty by a lower value, e,

(e<g). Consequently, a gap of length l will only

encounter a penalty of +

(

−1

)

 in this new

scheme.

2.3 Backtracking

Once the 3D scoring matrix has been filled, global

alignment(s) between the scanline and the image are

recovered by backtracking. This is achieved, first, by

retrieving in the matrix cell with the highest score

obtained for a global alignment. Then, from that cell,

using the stored direction information, one or more

paths are reconstructed to the origin of the matrix

and converted into alignments.

Global alignment scores are found in four planes

of the matrix (see Figure 6). If the last pixel of the

scanline corresponds to a pixel of the image, global

scores are recorded in the plane i = L (orange plane,

Figure 4). Alternatively, the end of the scanline may

not have any correspondence in the image because it

belongs to a non overlapping region. As a

consequence, the last scanline pixel with an image

pixel match would be located on one of the borders

of the image. This score could be read in either the

plane k = 1 (yellow plane, top of the image), the

plane k = H (green plane, bottom of the image) or

the plane j = W (purple plane, right of the image).

From the cell(s) with the highest score within

these four planes, global alignment are discovered

by backtracking inside the matrix using the stored

information regarding the direction(s) the score of

the cell of interest is coming from. Since a cell score

comes from the highest value among seven

directions, two or more directions could lead to

equal maximum scores. Consequently, during

backtracking several optimal alignments could be

produced. Although strategies, such as choosing the

solution which is the most consistent with this of the

DENSE PIXEL MATCHING BETWEEN UNRECTIFIED AND DISTORTED IMAGES USING DYNAMIC

PROGRAMMING

219

previous scanline, can be used to adopt the most

likely path, in this work, a unique alignment is

generated by selecting at random one of the global

solutions.

Figure 6: Location of global alignment scores.

3 EXPERIMENTAL RESULTS

In order to validate the proposed algorithm a set of

experiments were conducted. First, the algorithm is

evaluated using a standard stereo matching

evaluation framework using rectified images. Then,

the potential of our approach is demonstrated by

processing unrectified and non-linearly distorted

images.

Although parameters are optimised for each

stereo pair using the rectified image scenario, typical

values are m=256, g= 181 and e=156. Since the

processing of disparity maps by a median filter

increases accuracy by enforcing some inter-scanline

continuity (Veksler, 2005) (Deng and Lin, 2006), in

some experiments, we apply this filter in a post-

processing step.

3.1 Rectified Images

Our algorithm was first evaluated using the

Middlebury Stereo Evaluation framework

(Scharstein and Szeliski, 2003) which is widely used

as a benchmark tool by the computer vision

community when assessing performance of

matching algorithms between rectified images.

Initially, we validate our DP implementation by

disabling the ability of changing lines in the scoring

matrix. Therefore, it takes advantage of the fact that

images are known to be rectified. Table 1 shows

that, once a median filter is applied onto the raw

disparity maps, this basic version of the proposed

algorithm (Rectified), that was introduced in a

previous paper (Dieny, 2011), performs similarly to

Bobbick et al. (Bobick and Intille, 1999), which is

the reference among standard DP approaches.

Performances of the proposed algorithm

(Unrectified) are also provided in Table 1. Although

the ability to change lines degrades significantly

stereo matching accuracy, the quality of produced

disparity maps remains reasonable (Figure 7). In the

next section, we show that this performance

reduction in the case of rectified images is rewarded

by the ability to process more complex sets of image

pairs.

Figure 7: Raw disparity maps obtained for Middlebury

dataset (Unrectified).

Table 1: Performance comparison using the Middlebury

Stereo Evaluation framework.

Tsukuba

(non occ)

Venus

(non occ)

Teddy

(non occ)

Cones

(non occ)

Average

(bad pixels)

Bobbick

et al. 99

4.12 10.1 14.0 10.5 14.2

Rect.

6.74 10.7 14.1 11.0 16.7

Rect

4.63 7.40 10.7 7.75 13.4

Un-rect. 11.0 18.6 28.2 23.9 28.5

Un-rect

9.47 16.7 26.3 21.6 26.5

*: applying a Median Filter

3.2 Unrectified Images

The proposed algorithm has a unique capacity to

process unrectified and distorted images. This is first

demonstrated by applying rotations to the right

images of the Middlebury dataset (Scharstein 2002-

2003) to simulate unrectified images so that (see

Figure 8) quantitative results can be produced for

evaluation.

Since by design, the algorithm can only change

line by going either on the next pixel above or below

the current pixel, motions across an image are

limited to angles comprised in the interval [-45º,45º]

from the x axis. Consequently, an image rotation by

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

220

an angle outside that range cannot be directly solved.

However, this situation can be handled by using the

strategy described at the end of the section.

Figure 8: Raw Average pixel error for non occluded pixels

as a function of image rotation.

In Figure 8, average pixel error is depicted

according to the angle the right image was rotated.

Data are provided for the ‘Cone’ image with a 5º

resolution within the [-45º,45º] range, whereas the

other images are rotated with a 15º resolution within

the [0º,45º] range. Since the metrics employed in the

automatic evaluation framework are not publicly

available, error values reported in Figure 6 cannot be

directly compared to those shown in Table 1. Here,

we define average pixel error as the average

difference between the estimated and actual

disparity maps. Note that occluded pixels in either

map are not considered.

Consistent results are obtained for all the images

showing good performance for rotations within the

[-20º, 20º] range. Outside this range, pixel errors

increase significantly. This behaviour reveals some

weakness in the current penalty scheme used when a

change of line occurs, Eq. (2). When rotations by an

angle lower than 22.5º are applied, the scoring

matrix contains a majority of scanline moves and

consecutive line jumps are rare. However, in the

case of larger rotations, score inaccuracies

introduced by frequent line change affect

significantly the calculations of the scoring matrix

which leads to global errors in pixel

correspondences.

Although, by design, it is not possible to solve

alignments between images that have been rotated

by more than 45º, the framework can be easily

extended to tackle these situations. The strategy

relies on repeating the pixel correspondence process

after introducing artificial rotations. The original

right image is rotated 8 times by an angle of 45º so

that one of these 8 images will fall within the [-

45º,45º] interval when considering the combined

rotation, i.e. original plus artificial. Each of the 8

sets of correspondences is associated with an

average matching score calculated from maxima

found in the scoring matrices. These alignment

scores are them used to identify the meaningful

disparity map.

Figure 9 illustrates this with an example, where

the ‘cones’ right image was rotated by 60º. Analysis

of the curve shows that the best alignment score is

obtained when an artificial rotation of -45º is

applied: this corresponds to an actual combined

rotation of 15º, which can be successfully processed

by the proposed algorithm. This approach could also

be used to address the drop of performance caused

by images which were subjected to an original

rotation above 22.5º. In this application, artificial

rotations of 22.5º or lower would be required

Figure 9: Alignment scores obtained after adding an

artificial rotation (x axis).

3.3 Distorted Images

Given the general nature of our algorithm, its usage

is not limited to finding pixel correspondences

between unrectified images, but it can be applied to

images affected by non-linear distortions.

Figure 10: Correspondences in a distorted area: a) actual,

b) estimated c) disparity map.

DENSE PIXEL MATCHING BETWEEN UNRECTIFIED AND DISTORTED IMAGES USING DYNAMIC

PROGRAMMING

221

In order to illustrate this, three experiments were

conducted. First, water drops on a camera lens were

simulated by applying lenticular distortions to the

test image (Figure 13a,b). Then correspondences

between the original and the distorted images were

calculated. Figures 13c) and 10a,b) show that our

algorithm detects the distortions and find good

correspondences by seeking optimal alignment

within the image. The associated disparity maps

Figures 13b) and 10c) reveal our method identifies

not only distortion areas, but also their lenticular

nature, since disparity values tend to be higher in the

centres and radially decrease.

In the second experiment, a scene was captured

using different camera lenses (see Figure 1). The

second lens introduces a notable spherical aberration

(see Figure 1b) but also a small change of scale.

Figure 11 shows the result of matching three

scanlines of the first image (Figure 1a) against the

whole second image (Figure 1b). The central line

and two parallel lines at 60 pixels from the centre

were chosen to show the lens aberration and the

performance of our method under those conditions.

The proposed methodology allows us to find a

reasonable correspondence in spite of the distortion.

Figure 11: Global alignment between 3 scanlines and a

whole image in case of distortion. Green lines represents

the groundtruth while purple curves are calculated by our

algorithm.

Finally, in the third experiment, we processed the

picture of a standing lady and its retouched version

(Figures 12a,b), which shows a streamlined body.

This digital intervention is clearly identified on

Figure 12c and d) where the left and right parts of

the different limbs generally appear to have been

moved in opposite directions. In addition, dark

patches on Figure 12d highlights areas where a

cloning tool was applied to reconstruct missing

background.

Figure 12: Character a) before and b) after retouching.

Disparity maps c) Standard and d) using a colour palette

(enclosed) to highlight disparity directions.

4 CONCLUSIONS

In this paper, we introduce a novel algorithm for

dense pixel matching between unrectified images

without any pre-processing stage. Based on a

dynamic programming approach, our main

contribution is the design of a 3D scoring matrix

which allows finding the best correspondence

between a line and a whole image. As demonstrated

in experiments, good alignments are obtained using

images rotated by up to 20º and non-linearly

distorted. In addition, its structure, which relies on a

single DP process, makes it suitable for hardware

implementation.

As future work, we propose to improve the

current scoring scheme and exploit inter-scanline

information to improve the algorithm performance.

Thus, for instance, the usage of uniqueness

regarding the scanline matching would allow

accelerating the processing by excluding part of the

3D cube.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

222

Figure 13: Top left: a) Distorted image. Bottom Left: b) Disparity map between distorted and original images. Right: c)

Estimated correspondences.

REFERENCES

Ayache, N., Hansen, C., 1988. Rectification of images for

binocular and trinocular stereovision. In International

Conference on Pattern Recognition, pp. 11-16.

Baker, H., Binford, T., 1981. Depth from edge and

intensity based stereo. In IJCAI81, pp.631–636.

Barnard, S. T., Fischler, M. A., 1982. Computational

stereo. In ACM Comp. Surveys, 14(4), pp.553-572.

Barnum, P., Kanade, T., Narasimhan., S.G., 2007. Spatio-

Temporal Frequency Analysis for Removing Rain and

Snow from Videos. In PACV.

Belhumeur, P. N., 1996. A Bayesian approach to binocular

stereopsis. International Journal of Computer Vision,

19(3), pp.237–260.

Bobick, A.F., Intille, S.S., 1999. Large occlusion stereo.

International Journal of Computer Vision, 33(3),

pp.181–200.

Brown., L.G., 1992. A survey of image registration

techniques. In ACM Comp. Surveys, 24(4), pp.325-

376.

Brown, M.Z., Burschka, D., Hager, G.D., 2003. Advances

in computational stereo, IEEE Transactions on Pattern

Analysis and Machine Intelligence, 5 (8), pp. 993–

1008.

Cox, I. J., Hingorani, S. L., Rao, S. B., Maggs, B. M.,

1996. A maximum likelihood stereo algorithm.

Computer Vision and Image Understanding, 63(3),

pp.542–567.

Deng, Y., Lin, X., 2006. A fast line segment based dense

stereo algorithm using tree dynamic programming. In

European Conference on Computer Vision, Graz,

Austria, May 7 - 13.

Dhond, U. R., Aggarwal, J. K., 1989. Structure from

stereo: a review. In IEEE Trans. on Systems,Man, and

Cybern., 19(6), pp.1489-1510.

Dieny, R., Thevenon, J., Martinez-del-Rincon, J., Nebel,

J.C., 2011. Bioinformatics inspired algorithm for

stereo correspondence, In VISAPP, Vilamoura,

Portugal, March 5-7.

Duchaineau, M., Cohen, J., Vaidya, S., 2007. Toward Fast

Computation of Dense Image Correspondence on the

GPU. In High Performance Embedded Computing

Workshop, Lincoln Laboratory, Massachusetts

Institute of Technology, pp.91–92.Forstmann.

Forstmann, S., Kanou, Y., Ohya, J., Thuering, S., Schmitt,

A., 2004. Real-Time Stereo by using Dynamic

Programming, In Computer Vision and Pattern

Recognition Workshop, Washington, DC, USA, 27

June-2 July 2004.

Garg, K., Nayar, S. K., 2004. Detection and removal of

rain from videos. In CVPR.

Geiger, D., Ladendorf, B., Yuille, A., 1992. Occlusions

and binocular stereo. In European Conference on

Computer Vision, pp.425–433.

Gong, M., 2006. Enforcing Temporal Consistency in Real-

Time Stereo Estimation. In ECCV 2006, Part III,

LNCS 3953, pp.564– 577, 2006.

Hartley, R. I., 1999. Theory and practice of projective

rectification. International Journal of Computer

Vision, 35(2), pp.115–127.

DENSE PIXEL MATCHING BETWEEN UNRECTIFIED AND DISTORTED IMAGES USING DYNAMIC

PROGRAMMING

223

Jones. G. A., 1997. Constraint, Optimization, and

Hierarchy: Reviewing Stereoscopic Correspondence of

Complex Features. In Computer Vision and Image

Understanding, 65(1), pp. 57-78.

Lazaros, N., Sirakoulis, G. C., Gasteratos A., 2008.

Review of Stereo Vision Algorithms: From Software

to Hardware. International Journal of

Optomechatronics, 2(4), pp.435 – 462.

Lim, S. N., Mittal, A., Davis, L., Paragios, N., 2004.

Uncalibrated stereo rectification for automatic 3D

surveillance. In International Conference on Image

Processing, 2, pp.1357.

Lu, J., Ke Zhang, Lafruit, G., Catthoor, F. 2009. Real-time

stereo matching: A cross-based local approach. In

International Conference on Acoustics, Speech and

Signal Processing, pp.733-736, Washington, DC,

USA, April 19 - 24, 2009.

MacLean, W. J., Sabihuddin, S., Islam, J., 2010.

Leveraging cost matrix structure for hardware

implementation of stereo disparity computation using

dynamic programming. Computer Vision and Image

Understanding, In Press.

Needleman, S. B., Wunsch, C.D., 1970. A general method

applicable to the search for similarities in the

aminoacid sequence of two proteins. Journal of

Molecular Biology, 48(3), pp.443–53.

Note, J. B., Shand, M., Vuillemin, J., 2006. Real-Time

Video Pixel Matching. In FPL , pp. 1-6.

Ohta, Y., Kanade, T., 1985. Stereo by intra- and

interscanline search using dynamic programming.

IEEE TPAMI, 7(2), pp.139–154.

Oram., D., 2001. Rectification for Any Epipolar

Geometry. In BMVC, pp. 653-662.

Pollefeys, M., Koch, R., Van Gool, L., 1999. A simple and

efficient rectification method for general motion. In

International Conference on Computer Vision, vol 1,

pp. 496-501.

Roy, S., Meunier, J., Cox, I., 1997. Cylindrical

Rectification to Minimize Epipolar Distortion. In

Conference on Computer Vision and Pattern

Recognition, pp.393-399.

Salmen, J., Schlipsing, M., Edelbrunner, J., Hegemann, S.,

Lueke, S., 2009. Real-time stereo vision: making more

out of dynamic programming. In International

Conference on Computer Analysis of Images and

Patterns, Münster, Germany, Sept. 2-4.

Scharstein, D., Szeliski, R, 2002. A taxonomy and

evaluation of dense two-frame stereo correspondence

algorithms. International Journal of Computer Vision,

47(1), pp.7-42.

Scharstein, D., Szeliski, R, 2003. High-accuracy stereo

depth maps using structured light. In IEEE Computer

Society Conference on Computer Vision and Pattern

Recognition, vol. 1, pp. 195-202.

Sun, C., 2002. Fast Stereo Matching Using Rectangular

Subregioning and 3D Maximum-Surface Techniques.

In International Journal of Computer Vision archive,

47 (1-3), pp. 99-107.

Sun., C., 2002. Fast Optical Flow Using 3D Shortest Path

Techniques. In Image and Vision Computing,

20(13/14), pp. 981-991.

Tappen, M., Freeman, W., 2003. Comparison of graph

cuts with belief propagation for stereo, using identical

MRF parameters, in: IEEE International Conference

on Computer Vision (ICCV), 2, pp. 900–906.

Tippetts, B., Lee, D. J., Archibald, J., 2010. Fast

correspondence of unrectified stereo images using

genetic algorithm and spline representation. In

Intelligent Robots and Computer Vision XXVII:

Algorithms and Techniques, 7539, 17 January 2010.

Torr, P. H. S., Criminisi, A., 2004. Dense stereo using

pivoted dynamic programming. Image and Vision

Computing, 22(10), pp.795-806.

Vanetti, M., Gallo, I., Binaghi, E., 2009. Dense Two-

Frame Stereo Correspondence by Self-organizing

Neural Network. In ICIAP 2009, LNCS 5716,

pp.1035–1042.

Veksler, O., 2005. Stereo correspondence by dynamic

programming on a tree. In Computer Vision and

Pattern Recognition, San Diego, CA, USA, 20-26.

Willson, R. G., Johnson, A. E., Goguen, J. D., 2005.

MOC2DIMES: A camera simulator for the mars

exploration Rover descent image motion estimation

system. In Proc. 8th Int'l. Symp. Artificial Intelligence,

Robotics and Automation in Space.

Wan, D., Zhou, J., 2008. Stereo vision using two PTZ

cameras. Computer Vision and Image Understanding,

112, pp.184–194.

Wang, L., Liao, M., Gong, M., Yang, R., Nistér, D., 2006.

High-quality real-time stereo using adaptive cost

aggregation and dynamic programming. In 3D Data

Processing, Visualization and Transmission. Chapel

Hill, USA, June 14-16.

Yang, Q., Wang, L., Yang, R., 2006. Real-time Global

Stereo Matching Using Hierarchical Belief

propagation. In BMVC 2006, Edinburgh, UK.

Yaguchi, Y., Iseki, K., Oka, R., 2009. Optimal Pixel

Matching between Images. In PSIVT pp. 597-610.

Yin, X. C., Sun, J., 2007. Perspective Rectification for

Mobile Phone Camera-Based Documents Using a

Hybrid Approach to Vanishing Point Detection,

CBDAR'07, pp. 37-44.

Zhengping, J., 1988. On the multi-scale iconic

representation for low-level computer vision systems.

In PhD thesis, The Turing Institute and The University

of Strathclyde, 1988.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

224