A ROBUST TECHNIQUE FOR MULTIUSER DETECTION
IN THE PRESENCE OF SIGNATURE UNCERTAINTIES
Vinay Kumar P.
1
, Srinivasa Rao V.
2
, Balaji S.
3
, Habibulla Khan
3
and Anil Kumar T.
4
1
Department of ECE, MIC College of Technology, Kanchikacherla, 521180, Andhra Pradesh, India
2
Department of ECE, Anurag Engineering College, Kodad, 508206, Andhra Pradesh, India
3
Department of ECE, KL University, Vaddeswaram, 522502, Andhra Pradesh, India
4
Department of ECE, TRR Engineering College, Patancheru, 502319, Andhra Pradesh, India
Keywords: Influence Function, Non-gaussian Channels, Robust Multiuser Detection.
Abstract: This paper presents a robust multiuser detection technique to combat multiple access interference (MAI)
and impulsive noise for synchronous code-division multiple-access (CDMA) communication systems in the
presence of signature uncertainties. A new M-estimator (modified Hampel) proposed to robustify the
detector is studied and analyzed. The approach is corroborated with simulation results to evaluate the
performance of the proposed robust multiuser detector in comparison with the linear decorrelating detector,
Huber and Hampel estimator based detectors. Simulation results show that the new M-estimator based
detector offers significant performance gain over the linear decorrelating detector, the Huber, and the
Hampel estimator based detectors with little attendant increase in the computational complexity.
1 INTRODUCTION
Recent research has explored the potential benefits
of multiuser detection for code division multiple
access (CDMA) communication systems with
present multiple access interference (MAI) (Verdu,
1998). These optimal multiuser detectors have led to
the developments of the various linear multiuser
detectors with Gaussian noise though various
experimental measurements confirmed that many
realistic channels are impulsive in nature. Lately,
the problem of robust multiuser detection in non-
Gaussian channels has been addressed in the
literature (Wang and Poor, 1999), (Anil Kumar et
al., 2004), and (Anil Kumar and Deergha Rao,
2006), which were developed based on the Huber,
Hampel, and a new M-estimator (modified Hampel),
respectively. Recently, robust multiuser techniques,
that take into design consideration the effect of
signature mismatch at the receiver, have attracted a
great interest which includes the robust minimum
output energy (MOE) linear detector (Luo et al.,
2001), and a worst case performance optimization of
the MOE multiuser detector (Vorobyov et al., 2003;
Gershman and Shahbazpanahi, 2003). A new robust
nonlinear multiuser detector which minimizes the
worst-case (WC) probability of error across all
possible channel parameters in the region of
uncertainty is presented in (Salhov et al., 2004). A
robust CDMA multiuser detection technique based
on the probability-constrained optimization
approach is developed in (Sergiy, 2008).
Hence, this paper considers robust multiuser
detection in the presence of signature uncertainties
in non-Gaussian channels. A new M-estimator
proposed to robustify the multiuser detector is
presented. Performance gains offered by the
proposed approach are demonstrated through
simulation results. Simulation results show that the
new robust multiuser detector outperforms the linear
decorrelating detector, the Huber, and the Hampel
estimator based detectors.
The remaining portion of the paper is organized
as follows. Section 2 discusses the synchronous
CDMA system model with signature uncertainties
under non-Gaussian impulsive noise. Section 3
presents an M-estimator based regression and
influence functions of M-estimators. Section 4
discusses the simulation results and finally,
conclusion is drawn in section 5.
2 SYSTEM MODEL
An L-user synchronous CDMA system, where each
303
P. V., V. S., S. B., Khan H. and T. A..
A ROBUST TECHNIQUE FOR MULTIUSER DETECTION IN THE PRESENCE OF SIGNATURE UNCERTAINTIES.
DOI: 10.5220/0003813603030307
In Proceedings of the 2nd International Conference on Pervasive Embedded Computing and Communication Systems (PECCS-2012), pages 303-307
ISBN: 978-989-8565-00-6
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

user transmits information by modulating a signature
sequence, is considered in this paper. The received
signal over one symbol duration can be modelled as:
1
() () ∈
∑
L
lll
l=
rt = Abs+wt , t τ
(1)
where b
l
is the information symbol transmitted by
the l
th
user, s
l
(t) is the l
th
user spreading-code
waveform, A
l
≥ 0 is the received amplitude of the l
th
user’s signal, L is the number of users,
τ
is the
observation interval, and w
l
(i) is assumed as a
sequence of independent and identically distributed
(i.i.d.) random variables with a non-Gaussian
distribution. The probability density function of this
noise model has the form
22
(1 ) (0 ) (0 )f= -ε ,ν +ε ,κν ℵℵ
(2)
with
ν > 0, 0 ≤ ε ≤ 1, and κ ≥ 1. Here ℵ (0, ν
2
)
represents the nominal background noise and the
ℵ (0, κ ν
2
) represents an impulsive component, with ε
representing the probability that impulses occur. For
concreteness, we assume that b
l
∈[-1, 1]. At the
receiver, the resulting discrete-time signal in matrix
form is given by
,rSAbw=+
(3)
where S is the N×L matrix of columns s
l
, where the
vector s
l
contains the corresponding samples, A is
the diagonal matrix with diagonal elements A
l
> 0, b
is the data vector with components b
l
, and the vector
w contains the corresponding samples of the noise
process.
The purpose of multiuser detection is to detect
the symbols {b
l
} given the observed signal r
assuming that the diagonal matrix A and the
signature matrix S are known precisely at the
receiver. In practice, the signature vectors s
l
and the
diagonal matrix A may not be known exactly
because of channel distortion. Since the distorted A
can be directly translated to an appropriate signature
distortion, without loss of generality, signature
mismatch in the presence of non-Gaussian impulsive
noise is addressed in this paper. In the case of
signature matrix uncertainty, the received signal can
be written as (Salhov et al., 2004)
0
1
0
1
,
rS SAbw
HHbw
ii
i
ii
i
δ
δ
=
=
=+ +
∑
=+ +
∑
⎡⎤
⎢⎥
⎢⎥
⎣⎦
⎡⎤
⎢⎥
⎢⎥
⎣⎦
A
A
(4)
where H
i
=S
i
A, and δ
i
are perturbations that lie in
some perturbation set D. Since
δ
i
are not known
precisely, the error probability cannot be directly
minimized. The ML detector that minimizes the
worst-case error probability over all possible values
of
δ
i
is considered in (Salhov et al., 2004). Thus, we
seek the symbols that are solutions to the problem
given by (Salhov et al., 2004)
{}
()
1, 1
,
ˆ
arg min max ( ),
b
bHb
N
Dδ
δ
∈
∈−
=Δ
(5)
where
()
2
(), () .Hb rHbδδΔ=−
(6)
3 M-ESTIMATION BASED
REGRESSION
In M-estimates, unknown parameters θ
1
, θ
2
,... θ
L
(where
θ = Ab) are solved by minimizing a sum of
function
ρ (⋅) of the residuals
(
)
=1 =1
,
ˆ
=arg min -
∈ℜ
∑∑
NL
l
jjl
K
jl
θ
θρrsθ
(7)
where
ρ is a symmetric, positive-definite function
with a unique minimum at zero, and is chosen to be
less increasing than square. Suppose that
ρ
has a
derivative with respect to the unknown parameters
θ ( ψ = ρ′ ), called the influence function, since it
describes the influence of measurement errors on
solutions. The solution to (7) satisfies the implicit
equation (8), and its vector form is given in (9)
(
)
11
0 , 1...
==
−==
∑∑
NL
kl
jjkj
jk
rss lL ψθ
(8)
(
)
,−=SrSθ 0
T
L
ψ
(9)
where S
T
is the transpose of S and 0
L
is an all zero
vector of length L
. Equation (8) is called an
M-estimator. Different influence functions yield
solutions with different robustness properties.
Therefore, an influence function
ψ (⋅) should be
chosen such that it yields a solution that is not
sensitive to outlying measurements.
3.1 Influence Functions
M-estimators are generalizations of the usual
maximum likelihood estimates. In this subsection,
the influence functions of M-estimators proposed in
the literature (Wang and Poor, 1999; Anil Kumar et
PECCS 2012 - International Conference on Pervasive and Embedded Computing and Communication Systems
304

al., 2004; Anil Kumar and Deergha Rao, 2006) are
listed (see Figure 1). Huber’s, Hampel’s and the
proposed M-estimators are presented.
3.1.1 Huber’s Estimator
The Huber’s M-estimator is determined by the
Huber penalty function
ρ
HU
(⋅) and its derivative
given by
2
2
HU
2
() .
sgn( )
≤
=
>
⎧
⎪
⎨
⎪
⎩
x
for x k
x
kx forxk
ν
ψ
ν
ν
(10)
where k is any constant.
3.1.2 Hampel’s Estimator
Similarly, the Hampel’s M-estimator is determined
by the Hampel’s penalty function
ρ
HU
(⋅) and its
derivative given by
HA
sgn( )
() ,
sgn( )
0
≤
<≤
=
−
<≤
−
>
⎧
⎪
⎪
⎨
⎪
⎪
⎩
xforxa
ax foraxb
x
cx
ax forbxc
cb
for x c
ψ
(11)
where c is a constant.
3.1.3 Proposed Estimator
The proposed M-estimator (modified Hampel) is
determined by the penalty function and its
derivative, which is given, respectively, by
(Anil Kumar and Deergha Rao, 2006)
Figure 1: Influence function of (a) Huber estimator,
(b) Hampel estimator, and (c) the proposed estimator.
2
PRO
2
2
2
2
2
exp 1
2
( ) ,
⎧
⎪
≤
⎪
⎪
⎪
⎪
−
⎨
⎪
⎪
⎛⎞
⎪
⎜⎟
−+ >
⎪
⎜⎟
⎪
⎝⎠
⎩
=
<≤
xa
a
x
ab
db
b
x
for
a
x
xforaxb
for x
ρ
(12)
where d is a constant, and
PRO
2
2
sgn( )
() .
exp 1
⎧
⎪
≤
⎪
⎪
⎪
⎨
⎛⎞
⎪
⎜⎟
⎪
⎜⎟
⎪
⎝⎠
⎪
⎩
<≤
=
−>
xaxfor
ax foraxb
x
x
a
xforxb
b
b
ψ
(13)
The choice of the constants a (=κ
ν
2
) and b (= 2κ ν
2
)
depends on the robustness measures derived from
the influence function. A robust estimator should
possess a finite value of c (see Figure 1). The
proposed M-estimator is three-part with no sharp
rejection point c as in Hampel’s three-part re-
descending estimator. The proposed influence
function
ψ
PRO
(x) is bounded and has continuous
derivatives. The proposed detector has bounded
influence function, and hence is robust.
Asymptotic probability of error for the class of
decorrelating detectors described by (9) for large
processing gain N, is given by (Wang and Poor,
1999)
(
)
*1
,
ˆ
Pr 0 0
−
≡<>
=
⎛⎞
⎜⎟
⎜⎟
⎡⎤
⎜⎟
⎣⎦
⎝⎠
R
l
ell
l
ll
P
W
Q
θθ
υ
(14)
where Q(⋅) is the Gaussian Q-function defined
by
()
2
1
() /2 0
2
∞
≥
∫
x
Qx= exp-ξ dξ , x
π
, and
[]
2
2
2
.
() ()
() ()
∫
=
′
∫
ufudu
ufudu
ψ
υ
ψ
(15)
4 SIMULATION RESULTS
In Figure 2 and Figure 3, the performance of four
decorrelating detectors is studied by plotting the
probability of error versus the signal-to-noise ratio
(SNR) corresponding to the user 1 under perfect
power control of a synchronous system with six
A ROBUST TECHNIQUE FOR MULTIUSER DETECTION IN THE PRESENCE OF SIGNATURE UNCERTAINTIES
305

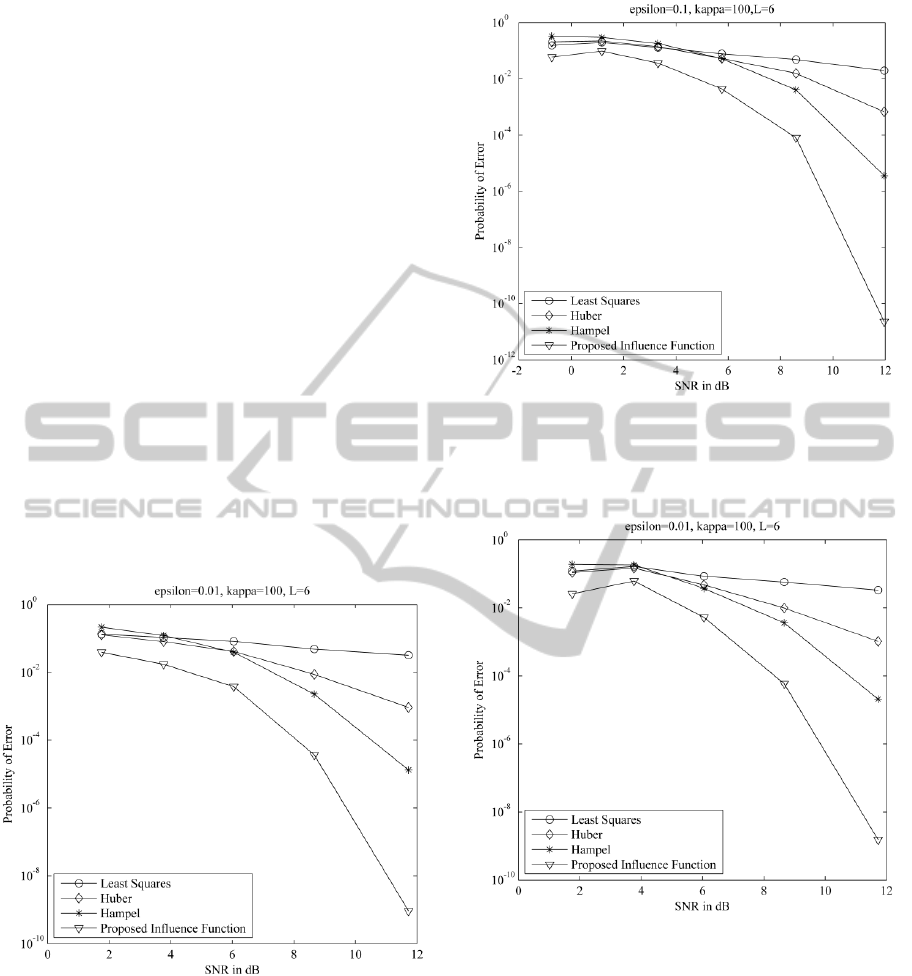
users (L = 6) and a processing gain of 31 (N =
31). The noise distribution parameters are
ε = 0.01
& κ = 100 and
ε = 0.1 & κ = 100 for Figure 2 and
Figure 3 respectively. These simulation results
demonstrate the performance gains achieved by the
minimax decorrelating detector with the proposed
influence function over the linear decorrelating
detector and minimax decorrelating detector (both
with Huber and Hampel estimators), in impulsive
noise. Moreover, this performance gain increases as
the SNR increases.
Further, an asynchronous system with six users
(L =6), processing gain of 31(N = 31), and the noise
distribution parameters
ε = 0.01 & κ = 100 and ε =
0.1 & κ = 100 (for Figure 4 and Figure 5
respectively) is considered. The delays of the 6
users are randomly generated. The proposed robust
multiuser detector, minimax decorrelating detector
(both with the Huber and Hampel M-estimators) and
the linear decorrelating detector are implemented.
It is seen from the simulation results that the
proposed multiuser detector offers substantial gains
over the minimax decorrelating detector (both with
the Huber and Hampel estimators) and the linear
decorrelating detector.
Figure 2: Probability of Error versus SNR for user 1 for
linear multiuser detector, minimax detector with Huber,
Hampel and proposed M-estimator in synchronous CDMA
channel with impulse noise, N=31, ε = 0.01.
Figure 3: Probability of Error versus SNR for user 1 for
linear multiuser detector, minimax detector with Huber,
Hampel and proposed M-estimator in synchronous CDMA
channel with impulse noise, N=31,
ε = 0.1.
Figure 4: Probability of Error versus SNR for user 1 for
linear multiuser detector, minimax detector with Huber,
Hampel and proposed M-estimator in asynchronous
CDMA channel with impulse noise, N=31, ε = 0.01.
PECCS 2012 - International Conference on Pervasive and Embedded Computing and Communication Systems
306

Figure 5: Probability of Error versus SNR for user 1 for
linear multiuser detector, minimax detector with Huber,
Hampel and proposed M-estimator in asynchronous
CDMA channel with impulse noise, N=31,
ε = 0.1.
5 CONCLUDING REMARKS
In this paper, a new M-estimator based robust
multiuser detection technique in the presence of
signature uncertainties is proposed, which
significantly outperforms the linear decorrelating
detector and minimax robust multiuser detector
(with Huber and Hampel M-estimators) in non-
Gaussian ambient noise. Simulation results show
that the proposed robust multiuser detector offers
significant performance gain over the linear
multiuser detector and the minimax decorrelating
detectors with Huber and Hampel M-estimator, in
non-Gaussian noise with little attendant increase in
the computational complexity.
REFERENCES
Verdu, S., 1998. Multiuser Detection, Cambridge
University Press, Cambridge.
Wang, X., Poor, H. V., 1999. Robust multiuser detection
in non-Gaussian channels. In IEEE Transactions on
Signal Processing, Vol. 47. No. 2, pp. 289-305.
Anil Kumr, T., Deergha Rao, K., Swamy, M. N. S., 2004.
A robust technique for multiuser detection in non-
Gaussian channels. In Proc. 47
th
Midwest Symposium
on Circuits and Systems, Vol. 3, pp. 25-28.
Anil Kumar, T., Deergha Rao, K., 2006, Improved robust
techniques for multiuser detection in non-Gaussian
channels. In Circuits Systems and Signal Processing
Journal, Vol. 25. No. 4.
Shuguang, C., Z hi-Quan, L., Zhi, D., 2001. Robust blind
multiuser detection against CDMA signature
mismatch. In Proc. Int. Conf. Accoust., Speech, Signal
Processing (ICASSP – 2001), Vol. 4, pp. 2297-2300.
Vorobyov, S. A., Gershman, A. B., Luo, Z. Q., 2003.
Robust adaptive beamforming using worst case
performance optimization. In IEEE Transactions on
Signal Processing, Vol. 51, pp. 313-324.
Gershman, A. B., Shahbazpanahi, S., 2003. Robust blind
multiuser detection for synchronous CDMA systems.
In Proc. Int. Conf. Acoust., Speech, Signal Processing.
Salhov, M., Wiesel, A., Eldar, Y. C., 2004. A robust
maximum likelihood multiuser detection in the
presence of signature uncertainties. In Proc. European
Signal Processing Conference (ESIPCO-2004), pp.
185-188.
Sergiy, A. V., 2008. Robust CDMA multiuser detectors:
Probability constrained versus the worst-case-based
design. In IEEE Signal Processing Letters, Vol. 15,
pp. 273-276.
A ROBUST TECHNIQUE FOR MULTIUSER DETECTION IN THE PRESENCE OF SIGNATURE UNCERTAINTIES
307