
SPARSE REPRESENTATIONS AND INVARIANT
SEQUENCE-FEATURE EXTRACTION FOR EVENT DETECTION
Alexandru P. Condurache and Alfred Mertins
Institute for Signal Processing, University of Luebeck, Ratzeburger Allee 160, Luebeck, Germany
Keywords:
Event Detection, Action Recognition, Invariant Feature Extraction, Sparse Classification.
Abstract:
We address the problem of detecting unusual actions performed by a human in a video. Broadly speaking, we
achieve our goal by matching the observed action to a set of a-priori known actions. If the observed action can
not be matched to any of the known actions (representing the normal case), we conclude that an event has taken
place. In this contribution we will show how sparse representations of actions can be used for event detection.
Our input data are video sequences showing different actions. Special care is taken to extract features from
these sequences. The features are chosen such that the sparse-representations paradigm can be applied and
they exhibit a set of invariance properties needed for detecting unusual human actions. We test our methods
on sequences showing different people performing various actions such as walking or running.
1 INTRODUCTION
We are interested in the detection of unusual human
behavior for security and surveillance applications.
Events are by definition sparse and it seems only nat-
ural to use sparse methods to detect them. The pur-
pose of this contribution is to prove that this concept
works and identify what specific requirements need to
be met along the way. To detect events, we harness
the discriminative nature of sparse representations.
Sparse representations are tributary to the principle
of parsimony. Sparsity as a data analysis and rep-
resentation paradigm is currently widely investigated
for various purposes like compressed sensing (Cand
`
es
and Tao, 2006; Donoho, 2006), but also feature ex-
traction (dAspremont et al., 2007), and data compres-
sion. Sparse representations have already been used
for recognition tasks by Wright et al. (2009) and
even for the recognition of human actions using data
from a wearable motion-sensor network by Yang et al.
(2008) or using video data (Guo et al., 2010). How-
ever, to the best of our knowledge, no link to event
detection was discussed before.
In our case, we first gather during training suffi-
cient video material to describe the actions we want
to recognize. A test video is represented as a lin-
ear combination of the training data, (i.e., of the vari-
ous actions in the training data) and recognized if the
representation contains mostly data from one single
training action. For event detection, where the train-
ing data covers the normal case, if all actions in the
training set are more or less equally present in our rep-
resentation we conclude we have observed an event.
To enable this procedure, for each frame a
sequence-feature vector is extracted from the chunk
of video consisting of the analyzed and the last R − 1
frames, on the basis of the contours of the silhouettes
of the acting person. Therefore we are able to la-
bel each frame of a test video, starting with the R’th.
Working frame based gives us the possibility to refine
the decision for an action, which usually extends over
many frames, by considering several frame decisions.
The feature-extraction process we propose here is de-
signed from the very beginning to generate a feature
space with a set of properties that are useful for event
detection. These are mainly properties of invariance
with respect to anthropomorphic changes, but also to
Euclidian motion in the image plane. At the same
time, we design our features such that they exhibit a
set of mathematical properties that make them suit-
able for sparse-representations-based event detection.
We assume that our video data has 24 fps and use
this to make several choices in our method, which
may otherwise appear random. Since our main pur-
pose is to prove that sparse representations are suited
for event detection and to set the frame for further re-
search in this direction, the data sets on which we test
our algorithms is less challenging than usual, but nev-
ertheless related to real practical scenarios (Gorelick
et al., 2007).
679
P. Condurache A. and Mertins A..
SPARSE REPRESENTATIONS AND INVARIANT SEQUENCE-FEATURE EXTRACTION FOR EVENT DETECTION.
DOI: 10.5220/0003817906790684
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 679-684
ISBN: 978-989-8565-03-7
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 SPARSE CLASSIFICATION
AND EVENT DETECTION
Sparse-representation based classification bares re-
semblances to nearest-subspace methods, which in
turn stem from nearest-neighbor classification.
Building on such premises, sparse-representation
based classification looks for the sparsest representa-
tion of a test vector in terms of a dictionary of train-
ing vectors. This representation is sparse because it
should contain only vectors from the class to which
the test vector belongs (Wright et al., 2009).
2.1 Sparse Classification
Let the training set be denoted by the matrix T =
[T
1
,...,T
k
], containing the class-submatrices T
i
=
[v
i,1
,...,v
i,N
i
] with i = 1, . . . , k, where N
i
is the num-
ber of vectors in class i and k the number of classes.
The total number of vectors in T is n =
∑
k
i=1
N
i
and
each vector v
i, j
, j = 1 . . . N
i
has m entries. Then, for
each new vector y that we want to classify, we ideally
have:
y = Tx
= x
i,1
v
i,1
+ ···+ x
i,N
i
v
i,N
i
(1)
where the coefficient vector x = [x
1,1
,...,x
k,N
k
]
T
of
length n has entries x
i, j
different from zero only for
the training-space vectors from the class i, to which
y belongs. This system of equations is usually over-
complete with the number n of vectors in the training
space being well larger than the dimension m of the
vectors. Thus, there are infinitely many solutions to
(1). Assuming equal number of training vectors per
class, the more classes the more sparse x. Thus we
do not search for some x, but for the sparsest vector
ˆx ∈ R
n
that solves equation (1). We find it by optimiz-
ing over the `
0
pseudo norm, solving:
ˆx = arg min k x k
0
subject to Tx = y. (2)
Ideally, assuming that a vector y is represented solely
with the training vectors from the correct class (that
is, the components of x corresponding to training vec-
tors from other classes are all zero), the vector y can
be classified by looking up to which class the nonzero
entries in x belong. In practice, of course, questions
about the required amount of sparsity and the unique-
ness of the sparsest solution arise. Donoho and Elad
(2003) showed that if some x with less than
m
2
nonzero
entries verifies y = Tx, then this is the unique sparsest
solution. This means that we have a good chance of
finding the correct and unique sparsest solution to (1)
even for two-class problems or for configurations in
which the number of training vectors per class is not
the same over all classes, provided we have enough
vectors in the training set.
The Decision. In practice, because the solution to
equation (2) is computationally difficult to find, we
solve instead:
ˆx = arg min k x k
1
subject to Tx = y (3)
Cand
`
es and Tao (2006) showed that minimizing over
the `
1
norm instead of the `
0
pseudo norm yields the
same solution if x is sparse enough.
The vector x found after we solve (3) will usually
have the largest entries for one class only, and small
non-zero entries for other classes as well. Next, we
use the following notation: 1
i
= [b
1
,...,b
n
]
T
, b
l
∈
{0,1}, l = 1, . . . , n is the selection vector for class i,
whose entries are everywhere zero, except for the po-
sitions of the columns of T that contain the training
vectors of class i, where they are one and v
1
v
2
is
the component-wise product of two vectors v
1
and v
2
.
Thus, 1
i
x selects the entries of x where the coeffi-
cients of class i reside. To assign a class label to the
vector y, we use C : R
m
→ {1,...,k} defined as:
C(y) = argmin
i
k y −T(1
i
ˆx) k
2
(4)
such that y is assigned to the class whose training-set
vectors best reproduce it (Wright et al., 2009).
2.2 Event Detection
The “Unsure” Decision. If a test vector cannot
be assigned with sufficient confidence to any of the
classes represented in T, then it receives the label “un-
sure”. In order to express such a confidence, for the
decision rule in (4), a sparsity concentration index is
defined as
SCI(x) =
l max
i
k 1
i
x k
1
k x k
1
− 1
l − 1
(5)
The vector is labeled “unsure” when SCI(x) ≤ τ. The
parameters l and τ need to be set empirically.
Decision for a Data Sequence. Until now we have
discussed how to decide for a test vector. If the data
we analyze is a sequence of vectors (e.g., one for each
video frame) we need to adapt our decision. Then, we
consider a time window of L vectors in the beginning
of the sequence and decide for the class that yields
a majority among these vectors, while ignoring “un-
sure” decisions. If all decisions are ”unsure”, then the
sequence is classified as ’unsure”.
Event Detection. Should a single test vector be la-
beled as unsure, then this is equivalent to detecting
an event, assuming the normal case is properly cap-
tured in the vectors of the training matrix T. For our
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
680

purposes, should a sequence of vectors be labeled as
unsure, then this is equivalent to detecting an unusal
action, i.e., an event.
3 INVARIANT FEATURE
EXTRACTION
We use here features based on Fourier descriptors
(FD) (Arbter et al., 1990) computed from the contour
of the acting person. Because we analyze sequences,
the final sequence-feature vector, corresponding to
one frame, contains information from a set of R con-
secutive frames, including the current one. These fea-
tures are chosen such that they exhibit some invari-
ance properties needed for event detection. A feature
vector is computed for every frame of video starting
with the R’th.
Contour Extraction and the Fourier Spectrogram.
The features we extract should describe human ac-
tions. These actions take place under various illu-
mination conditions, and are conducted by persons
wearing differently-textured clothes. To achieve in-
variance over such conditions we extract our features
from the contour of the acting person.
To find the contour, assuming the human is the
only object moving in our video and the back-
ground is available, we first compute a binary mo-
tion mask B by subtracting the background from
the current frame and comparing the result with a
threshold (Otsu, 1979). We obtain the contour C =
[(x
1
,y
1
),...,(x
n
C
,y
n
C
)]
T
with n
C
contour points by
subtracting the eroded motion mask from the orig-
inal, where the erosion uses a cross-like structur-
ing element. We compute the FDs for the contour
as:θ(ω
p
) = F (C
c
) =
∑
n
C
i=1
u
i
e
− jω
p
i
with ω is the an-
gular frequency, C
c
= [x
1
+ jy
1
,...,x
n
C
+ jy
n
C
]
T
is the
complex representation of the contour and F is the
Fourier operator. As features ϑ
f
for frame f we keep
only the magnitudes of Q descriptors – half for the
negative and half for the positive frequencies, exclud-
ing the DC component: ϑ
f
= [|θ
1
|,...,|θ
Q
|]
T
We want to extract sequence-features, for which
purpose we introduce next the Fourier descriptors
spectrogram (FDS). Considering the data on which
we demonstrate our algorithm, we assume the an-
alyzed actions have a certain periodicity, extending
over at most R frames. Thus, different time win-
dows of length R from the video of the same per-
son, conducting the same action, contain chunks of
the same periodic signal, but with various phases. To
compute our sequence-feature vector, we gather the
frame-feature vectors from R frames in a matrix with
Q lines and R columns. We call this matrix the Fourier
descriptors spectrogram: FDS =
ϑ
1
,...,ϑ
R
. Using
only the magnitudes of the FDs, the FDS is invariant
to several operations, including starting point, rota-
tion and translation.
3.1 Invariant Sequence Features
Viewpoint changes, scale variations but foremost the
anthropometric characteristics of various persons lead
to changes in the acquired contours. Our method
should be invariant to such changes. To introduce
the needed invariances into our algorithm, we make
use of invariant integration as described by Schulz-
Mirbach (1992). Invariant integration returns features
invariant to the actions of a group of transformations
on an input signal. For this purpose we define a fea-
ture function f (·) on the signal space and integrate
it over the group of actions. Schulz-Mirbach (1994)
shows that the set of monomials m(·) is a good choice
for f (·). For a D-dimensional input t = [t
1
,...,t
D
],
the monomials are defined as m(t) =
∏
D
d=1
t
b
d
d
, where
b
d
∈ N. Invariant integration is a powerful tool with
a wide range of applications including the analysis
of observation sequences, as shown by M
¨
uller and
Mertins (2011) for speech data.
A Model for Anthropometric Changes. We define
the group of transformations to which we achieve in-
variance in relation to the effects that anthropomet-
ric changes have on the contour of the person. At
this stage, we model anthropometric changes by the
convolution of the contour with pairs of Dirac pulses,
where the distance between the two pulses is variable.
Thus, we would like to achieve invariance to sinusoids
modulating the FDs. Multiplication of the FDs with
a sinusoid is equivalent to a shift of the Fourier coef-
ficients of the FDs. Therefore, we need to compute
features invariant to shifts of the Fourier transform of
the FDs. We first compute the Fourier transform of
the columns of FDS, obtaining thus:S = F
c
(FDS) =
[ϕ
1
,...,ϕ
R
], with ϕ = [φ
1
,...,φ
Q
]
T
. Next, we apply
invariant integration on the columns of S and consider
only the magnitudes. By integrating over all shifts
from 1 to Q, while enforcing suitable boundary con-
ditions, we achieve invariance to a set of modulating
sinusoids of various frequencies.
The Feature Function. For our purposes, we use
monomials of order two. Thus, b
d
= 0, for d ∈
{1,2,...,Q}\{q
1
,q
2
} and b
d
6= 0 for d ∈ {q
1
,q
2
}.
For better separability, various monomial features
SPARSE REPRESENTATIONS AND INVARIANT SEQUENCE-FEATURE EXTRACTION FOR EVENT
DETECTION
681
(i.e., different values for q
1
and q
2
) are used, obtain-
ing for each column of S an invariant feature vector
with one entry per monomial. Here, we need a scalar
feature for each column from S , thus, we define our
feature function M (·) to be a linear combination of
monomials. To obtain class-conditional distributions
and thus a feature space that is better suited for the
sparse classifier, we chose b
d
∈ R, instead of b
d
∈ N.
Our feature function consists of a linear combina-
tion of three monomials m
i
, i = 1 . . . 3, from various
entries along the columns ϕ
r
, r = 1, . . . , R of S . For
m
1
, we use q
1
= q and q
2
= q−1 with b
q
1
= b
q
2
= 1.7,
for m
2
we use q
1
= q and q
2
= q − 3 with b
q
1
=
b
q
2
= 1.5 and for m
3
we use q
1
= q and q
2
= q − 5
with b
q
1
= b
q
2
= 1.3. The index q runs over the en-
tries of ϕ
r
. The feature function is then: M (ϕ
r
;q) =
(φ
r
q
φ
r
q−1
)
1.7
+(φ
r
q
φ
r
q−3
)
1.5
+(φ
r
q
φ
r
q−5
)
1.3
, q = 1, . .. , Q,
with periodic boundary conditions.
To compute the sequence feature we should inte-
grate over this feature function. Integration is numer-
ically approximated by summation, which is in turn
unnormalized mean computation. For our features we
use more robust order statistics instead of integration.
The sequence-feature vector is computed by taking
the 25’th percentile over the combinations of mono-
mials: v
r
= p
25
(M (ϕ
r
;q)). Therefore, for the entire
S, we get, an R-dimensional sequence-feature vector
v = [v
1
,...,v
R
]
T
that is invariant to a set of anthropo-
metric variations.
The parameters of the feature function and the pre-
cise percentile were empirically chosen on the data-
set we’ve used to test our methods.
4 EXPERIMENTS
We test our methods on part of the KTH action
database (Schuldt et al., 2004). This database con-
tains six types of human actions (walk, jogg, run, box,
hand wave and hand clapp) performed by 25 persons.
We use the walk (W), jogg (J) and run (R) actions.
Each person performs the action four times: three
times outdoors and one time indoors. We have used
the outdoor sequences where the person moves paral-
lel to the camera. Therefore, for each action we have
25 action-sequences (one for each person) in our data
set. We extract one sequence-feature vector per frame
of video obtaining a classification result for each an-
alyzed frame. The decision for a multi-frame action-
sequence is taken as for a data sequence.
We divide our experiments into: feature extrac-
tion, action-sequence recognition and point-event de-
tection. For action-sequence recognition, the query
action sequence is already in the training set – this
(a) (b) (c) (d)
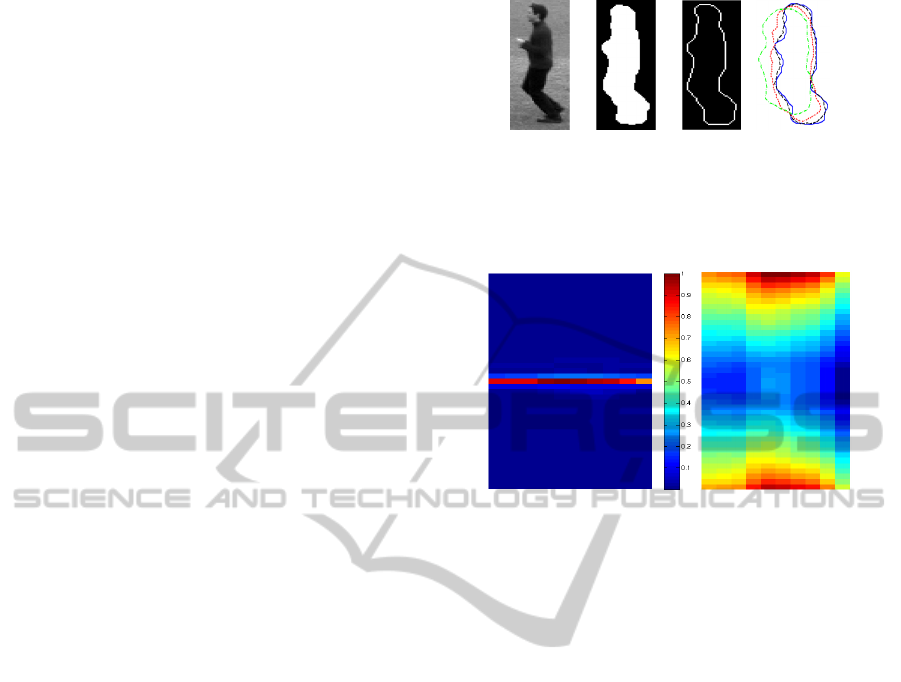
Figure 1: Motion region in a frame (a), motion mask (b)
and its contour (c). Original contour (continuous blue line)
and and variations to which we are invariant after invariant
integration (interrupted lines), applied to the S (d).
(a) (b)
Figure 2: FDS (a) and |S | (b).
would also be the scenario in which these methods
are used as a building block for context and collective
event detection algorithms. For point-event detection,
the analyzed action sequence is not in the training
set and is significantly different from other action se-
quences in the training set. To compute the SCI, we
use equation (5) with l = 10. For the “unsure” deci-
sion we use τ = 0.4.
4.1 Feature Extraction
After motion detection, we obtain a motion mask
(Figure 1 (b)). That we use to detect the contour of
the moving person (Figure 1 (c)). The contour is fur-
ther used to compute the FDs with Q = 40 and the
FDS (Figure 2 (a)) with R=10 that in turn yields |S |
(Figure 2 (b)), and after the invariance transform, our
feature vector (Figure 3 (b)).
By using the magnitudes of the FDs we are al-
ready invariant to a set of variations of the original
contour. The invariance transform achieves that the
corresponding feature vector is invariant to several
more contour variations. Some of these additional
variations are shown in Figure 1 (d).
4.2 Action Recognition
We have conducted two experiments. In the first ex-
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
682
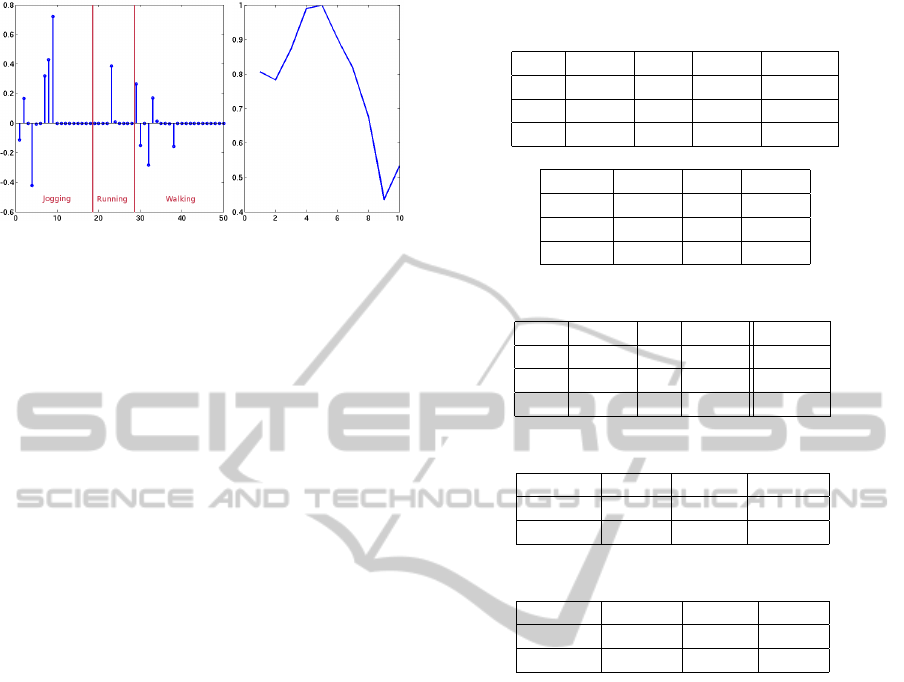
(a) (b)
Figure 3: The coefficient vector for a frame from a jogging
sequence with decision regions (a) and our feature vector
(b).
periment we look at how is each video frame classi-
fied. In the second we use the frame decisions to clas-
sify action sequences, with L = 24. The results were
computed by means of the leave-one-out method. The
procedure was repeated until every point from the
available data set was used for testing once. To com-
pute the training matrix, we used for jogging the first
nine frames of each sequence, for running the first five
of each sequence and for walking the first eleven of
each sequence. A coefficient vector resulting from a
training space with two action sequences per action
type is shown in Figure 3(a).
We have computed the permutation matrices for
the types of sequences we have worked with. The per-
mutation matrices should be read along lines, e.g., for
the action of jogging, the first column contains correct
decisions, the second wrong decisions in favor of the
class labeled “Running” and the third column wrong
decisions in favor of the class labeled “Walking”. For
the frame experiment, on average 32% of all frames
in a sequence are labeled as “unsure”. In Table 1(a)
we show results including the “unsure” frames and
in Table 1(b) we show results ignoring the “unsure”
frames. For the sequence experiment, the results are
shown in Table 2. For the sequences labeled as “un-
sure”, all first 24 frames were labeled as ’unsure’.
4.3 Event Detection
For event detection we have conducted two experi-
ments: for the first one, we have used two types of
actions to simulate the normal case and the event was
the third (e.g., running and walking were normal and
jogging was an event) and for the second one, we have
used one type of action as normal case, and the other
two were the event. The results for the first experi-
ment are shown in Table 3 and for the second, in Ta-
ble 4. These tables show the percentage of sequences
correctly classified as event. The results are obtained
Table 1: Permutation matrices for frame decisions.
(a) Results including “unsure” frames
(%) J R W unsure
J 36.79 3.28 18.99 40.94
R 0 75 0 25
W 2.72 0.98 65.38 30.92
(b) Results ignoring “unsure” frames
(%) J R W
J 62.36 5.56 32.19
R 0 100 0
W 3.84 1.42 94.75
Table 2: Permutation matrix for action-sequence decisions.
(%) J R W unsure
J 86.67 0 13.33 0
R 0 60 0 40
W 0 0 100 0
Table 3: Event-detection results for the first experiment.
Normal J & R J & W R & W
Event W R J
(%) 100 73.33 86.67
Table 4: Event-detection results for the second experiment.
Normal J R W
Event R & W W & J R & J
(%) 96.67 100 86.67
by a modified type of five fold cross-validation. At
each iteration, the training matrix is composed of five
different “normal” action-sequences and the event set
is given by all 25 “event” action-sequences. In the end
we compute the average of the detection rates.
5 DISCUSSION CONCLUSIONS
AND SUMMARY
Since a step during walking takes some ten frames,
we choose the number of columns of the FDS to be
R = 10. For each of the L = 24 frames needed to
take a sequence decision, a feature vector is extracted
from ten frames (nine previous frames and the cur-
rent one). Thus, a decision for a sequence is taken
after 34 frames have been recorded. Clearly, to an-
alyze a sequence in the current setup, a minimum of
at least ten frames is needed, in which case the deci-
sion for the 11’th frame is the decision for the entire
sequence. Extracting the sequence features from ten
frames is well suited for the current data. The number
of frames to be considered for a sequence-feature vec-
SPARSE REPRESENTATIONS AND INVARIANT SEQUENCE-FEATURE EXTRACTION FOR EVENT
DETECTION
683

tor should be chosen in relation with the frame rate of
the analyzed video and the length of an atomic part of
the analyzed action (in this case one step of the per-
son executing the action) and validated on the train-
ing data. Deciding for a sequence based on a major-
ity of frame-decisions from the first 24 frames proved
well suited for the current data set. As a rule of the
thumb, the more frames are considered, the better the
sequence-decision. During feature extraction, we use
Q = 40 FDs left and right from zero and hence implic-
itly assume a minimal contour length for a certain im-
age resolution. This number of FDs is well suited for
our data, but it should be chosen according to these
considerations in practice. All parameters with no
rules for determining them were established by six-
fold cross validation using the videos of the first 10
persons.
Our feature vector is invariant to several variations
of the person’s contour, some corresponding to an-
thropometric changes, however, some can be thought
of as corresponding to viewpoint changes and to scale
changes and thus we obtain also a mild viewpoint in-
variance in our feature vector.
A decision for a sequence of around 50 frames is
available after 47 seconds under MATLAB on a 2.66
GHz dual-core machine. However, many of the algo-
rithmic steps can be conducted in a parallel manner.
The sparse classification paradigm can be used
for action recognition and to detect all sort of point
events. While not directly suited for context and col-
lective events, it may represent an action-recognition
building block for such algorithms, other blocks be-
ing necessary for analyzing the chains of individual
actions (Matern et al., 2011). The particular feature
extraction process we use here is specific for the anal-
ysis of human behavior. We are concerned with the
behavior of a person in a single track and the current
feature extraction is adapted for this case. A prerequi-
site for deploying these methods in more complicated
scenarios is a successful tracking, irrespective of the
number of cameras used.
Our algorithm can be seen of consisting of two
parts: feature extraction and sparse classification. The
feature extraction is targeted to certain invariances
and tailored to the sparse classifier. We have shown
that sparse classification as introduced by Wright et
al. (2009) is well suited for human event detection.
Sparse classification offers a set of advantages over
other methods for the problem of action recognition
and event detection, being robust, adaptive and easy
to tune. In this context, the focus is now set on the
extraction of suitable features to enable the usage of
such methods. Furthermore, even if the issue of in-
variance can be addressed at the classifier level when
using sparse classifiers, many of the desirable invari-
ance properties that characterize a good human ac-
tion recognition/event detection method should be ob-
tained by means of the feature extraction process. We
have shown how to use the invariant integration as de-
scribed by Schulz-Mirbach (1992) to extract such fea-
tures from the contour of the acting person.
REFERENCES
Arbter, K., Snyder, W., Burkhardt, H., and Hirzinger, G.
(1990). Application of affine-invariant fourier descrip-
tors to recognition of 3-d objects. IEEE Trans. Patt.
Anal. Mach. Intell., 12:640–647.
Cand
`
es, E. and Tao, T. (2006). Near-optimal signal re-
covery from random projections: Universal encoding
strategies? IEEE Trans. Inform. Theory, 52(12):5406–
5425.
d’Aspremont, A., Ghaoui, L. E., Jordan, M., and Lanckriet,
G. (2007). A direct formulation of sparse pca using
semidefinite programming. SIAM Review, 49(3).
Donoho, D. (2006). Compressed sensing. IEEE Trans. In-
form. Theory, 52(4):1289–1306.
Donoho, D. and Elad, M. (2003). Optimal sparse repre-
sentation in general (nonorthogonal) dictionaries via
`
1
minimization. Proc. Nat’l Academy of Sciences,
pages 2197–2202.
Gorelick, L., Blank, M., Shechtman, E., Irani, M., and
Basri, R. (2007). Actions as space-time shapes. Trans.
Patt. Anal. Mach. Intell., 29(12):2247–2253.
Guo, K., Ishwar, P., and Konrad, J. (2010). Action recog-
nition using sparse representation on covariance man-
ifolds of optical flow. In Proc. AVSS, pages 188–195.
Matern, D., Condurache, A. P., and Mertins, A. (2011).
Event detection using log-linear models for coronary
contrast agent injections. In Proc. ICPRAM.
M
¨
uller, F. and Mertins, A. (2011). Contextual invariant-
integration features for improved speaker-independent
speech recognition. Speech Comm., 53(6):830 – 841.
Otsu, N. (1979). A threshold selection method from gray-
level histograms. IEEE Trans. on Sys., Man and Cyb.,
SMC-9(1):62–66.
Schuldt, C., Laptev, I., and Caputo, B. (2004). Recognizing
human actions: A local svm approach. Proc. ICPR,
3:32–36.
Schulz-Mirbach, H. (1992). On the existence of complete
invariant feature spaces in pattern recognition. In
Proc. ICPR, volume 2, pages 178–182, The Hague.
Schulz-Mirbach, H. (1994). Algorithms for the construction
of invariant features. In DAGM Symposium, volume 5,
pages 324–332, Wien.
Wright, J., Yang, A., Ganesh, A., Sastry, S., and Ma, Y.
(2009). Robust face recognition via sparse representa-
tion. IEEE Trans. Patt. Anal. Mach. Intell., 31(2):210–
227.
Yang, A., Jafari, R., Sastry, S., and Bajcsy, R. (2008).
Distributed recognition of human actions using wear-
able motion sensor networks. J Amb. Intl. Smt. Env.,
30(5):893–908.
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
684
