MOBILITY ASSISTED COVERAGE RESTORATION SCHEME

IN WIRELESS SENSOR NETWORKS

Eman AlQuraishi, Paulvanna N. Marimuthu and Sami J. Habib

Kuwait University, Computer Engineering Department, P. O. Box 5969, 13060, Safat, Kuwait

Keywords: Mal function, Coverage, Restoration, Optimization.

Abstract: In this paper, we have examined the problem of simultaneous failure of sensors within the wireless sensor

networks (WSN), whereby the sensors failures are due to malfunction or electrical faults. We have proposed

a mobility assisted coverage restoration algorithm, which restores the coverage of the failed sensors without

adding new sensors. The proposed algorithm follows two phases; clustering and restoration. The clustering

phase groups the failed sensors with their proximity, and then it relocates them into cluster. The restoration

phase moves the nearby active sensor with higher energy to the center of the cluster of failed sensors and

doubles its sensing area to restore the coverage. The restoration scheme exploits the mobility of the sensors

to form clusters of failed sensor, which reduce the number of restoring sensors, thereby prolonging the

lifespan of the network. Experimental results indicate that for a small size WSN comprising of 25 nodes and

nine nodes of it failing simultaneously, our restoration algorithm is able to increase the coverage area from

34% to 86% at the expense of small reduction in the lifespan estimated to be 24% of the network.

1 INTRODUCTION

We are concerned with the restoration of multiple

sensor failures due to electrical faults or

malfunctions in mobile wireless sensor network. In a

work by Habib and PaulvannaNayaki (2010), the

sensors are fixed and a neighborhood active sensor

is utilized to double its sensing radius to restore the

area of the failed sensors. However, the coverage

restoration by doubling of neighboring sensing

radius results in additional energy consumption with

increasing overlapping area, and it further increases

energy consumption with increase in sensor failures.

In this paper, we have considered a wireless

sensor network with mobile sensors, and we have

proposed a mobility assisted coverage restoration

scheme to restore the uncovered area with minimal

active sensors. The simultaneous failure of more

than one sensor results in the development of

uncovered area. The restoration scheme comprises

of two phases. The clustering phase groups the failed

sensors together to form an immediate neighboring

set. The restoring phase moves active sensors with

higher energy to the location of cluster of failed

sensor and doubles its sensing radius to restore

uncovered area. Clustering followed by restoration

reduces the number of active sensors necessary to

double their sensing radius, thus our restoration

method maximizes the coverage area with minimal

energy consumption. Our simulation results show

that for a given wireless sensor network comprised

of 25 sensors and 9 sensors failing simultaneously,

our restoration algorithm increases the total

coverage area by 52% on comparison with the non-

restoration environment.

2 WSN MODEL

The service area to be monitored by sensors is

divided into N x N cells and the given K sensor

nodes denoted by black dots are placed at the center-

of-mass of each cell to cover the service area more

efficiently as illustrated in Figure 1. The sensing

area is assumed to be circular and the sensing range

of each sensor node is confined within its cell by

gray circles. The area of each cell is presented as

width (W) x height (H) sq. units. The total service

area is N² x W x H. For simplicity, we assume that

each cell is a square (W=H) and the area of each cell

is equal to W² (or H

). We follow the coverage

restoration model in (Habib and PaulvannaNayaki,

2010) to estimate the coverage area.

AlQuraishi E., N. Marimuthu P. and J. Habib S..

MOBILITY ASSISTED COVERAGE RESTORATION SCHEME IN WIRELESS SENSOR NETWORKS.

DOI: 10.5220/0003818000870090

In Proceedings of the 1st International Conference on Sensor Networks (SENSORNETS-2012), pages 87-90

ISBN: 978-989-8565-01-3

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

The area covered by each sensor with circular

sensing area is given by Equation (1) and the total

area covered by the given sensors is represented by

Equation (2).



r









, where r=w/2 (1)

Total area covered by K sensors =

















(2)

In Equation (2), we assume that each cell is

occupied by a sensor, thereby K equals N² and the

total covered area is N² * π * W²/4. The coverage

area is computed as the ratio of the total area

covered by the sensors to the total area of the grid.

In this paper, we assume that each sensor has the

capability to move from one cell to another cell

(mobility). Initially, the sensors are with equal

sensing radius, but with various energy levels;

therefore, the sensors possess diverse lifespan. The

source of power for each sensor depends on three

AAA batteries as in the case of a prototype mobile

sensor. According to Wang et al., (2005), initial

residual energy of the sensors is distributed between

10000J and 16000J and mobile sensor can have a

speed of 2m/s with the energy consumption of

moving one meter is estimated to be equal to 27.96J.

Furthermore, we assume that the sensing radius is

adjustable, and it can be increased or decreased.

However, the increase in the sensing range increases

the power consumption.

Figure 1: The wireless sensor network model.

3 PROBLEM FORMULATION

The main objective function of the coverage

restoration problem is to maximize the coverage area

with reduced energy consumption as stated in

Equation (3). The numerator represents the total area

) covered by the active deployed sensors and the

denominator represents the given network area,

which is the area of the given square grid.

Max





(3)

Here, we highlight four constraints, which are added

to reduce the energy consumption during sensor

mobility and restoration. The first constraint places

an upper bound D on the distance moved by any of

the given sensor, and it is given by d < D, where d

be the Euclidean distance moved by a sensor from

location (x

, y

) to location (x

, y

). This constraint is

added to limit the movement of sensors to a far

location within the network, thereby minimizing the

power consumption.

The second constraint verifies the upper bound

on sensing range of a sensor and it is defined as r

R for every sensor i in the network. The terms r

and

R are the sensing range of sensor i and its upper

bound on sensin range respectively. This constraint

aims at balancing the power consumption between

the sensor nodes with increasing sensing radius. The

third constraint states a lower bound on the lifetime

of the network and is given by

min

TT 





Ki

TT where

Where T is the sum of lifespan of the active sensors

within the network and T

min

is the minimum allowed

lifespan of the network. K is the number of deployed

sensors. It ensures that the restoration operation is

allowed only if the lifespan of the network is

sufficiently above the given lower energy bound.

In this model, it is assumed that the sensors are

active for one hour daily and they are idle (sleep) for

remaining 23 hours. The sensors consume 102µA in

sleep mode and 77mA in active mode (Jia et al.,

2009). The daily energy consumption for each active

sensor is calculated as 53.5 Joules/day. The lifespan

T of the network (in days) is given as in Equation

(4), where

is the total residual energy of the

network and

is the energy consumed till that day.

T 

days

(4)





, where E

is the energy of the sensors

present at the time of measurement and K

represents the total active sensors at that time.

With doubling of sensing range, the energy

consumption in active mode increases by certain

percentage (X). The fourth constraint is added to

limit the number of failing sensors at any time. The

number of failing sensors should be less than the

SENSORNETS 2012 - International Conference on Sensor Networks

total number of deployed sensors: M < K, where M,

K are the number of failed sensors and the total

number of deployed sensors, respectively.

4 ANALYSIS OF SENSOR

FAILURES

The distribution of failed sensors within the given

WSN area is classified as clustered and sproadic.

Our restoration algorihtm analyzes the given sensor

network with multiple sensor failures, before

applying the restoration algorithm. If the failed

sensors are clusters by themselves as illustrated in

Figure 2, then each failed node is a neighbor to at

least one of the remaining failed node within the

cluster. If the failed sensors are distributed randomly

as shown in Figure 3, then they are sporadic.

5 COVERAGE RESTORATION

ALGORITHM

We have proposed a mobility assisted restoration

algorithm to restore the coverage area of the failed

sensors, whereby the sensor with highest energy is

allowed to move to the location of the failed clusters

and double its sensing radius to restore the coverage.

The resoration algorithm clusters the failed sensors

before applying the resotration procedure to

minimize the number of restoring sensors.

Figure 2: Clustered failure. Figure 3: Sporadic failure.

Figures 4 and 5 show the series of operations on

sporadic failure of four sensors as shown in Figure 3

to cluster the failed sensors and then restore the

network with two active sensors. The presence of

active sensors in between the failed sensors as

shown in Figure 3 necessitates the movement of

active sensors to nearby locations so that the failed

sensors form a cluster. In this case, two sensors with

doubled sensing range may be sufficient to cover the

failure of the four sensors.

Figure 4: Swapping

active and failed

sensors.

Figure 5: Restoration.

To balance the energy consumption and prevent

any sensor from being drained out of energy, we

have proposed a scheduling algorithm to schedule

the swapping operation between the active sensors

with doubled radius and with the nearby active

sensors possessing higher energy at the recovery

point.

6 RESULTS AND DISCUSSION

We have coded the restoration algorithm in C++. We

have considered a WSN network with a grid size of

4x4, which is comprised of 16 active sensors

initially. The sensing radius for each sensor is of 2m.

The coverage area and energy levels are updated

every day throughout the lifetime of the network for

three different scenarios; without failure (normal

operation), with failure but without restoration, and

with failure and with restoration. Out of 16 sensors

in the network, we have considered the simultaneous

failure of 9 sensors generated randomly and applied

the clustering and restoration algorithm to restore the

coverage area. Figure 6 illustrates the area coverage

against the lifespan of the network in all the three

categories, where we observed that the failed sensors

with restoration have showed the highest coverage in

most of the days, which is even higher than the

coverage achieved in normal operation. The increase

in area is achieved through the additional coverage

of the corner area of the squared cell, which is not

covered in normal operation.

The simultaneous failure of 9 sensors decreases

the coverage area from 78% to 34%. With the

restoration algorithm, the coverage area has

increased from 34% (failure with no restoration) to

86% (failure with restoration), which corresponds to

52% increase in the coverage area. However, with

oundary

oin

Center

oin

MOBILITY ASSISTED COVERAGE RESTORATION SCHEME IN WIRELESS SENSOR NETWORKS

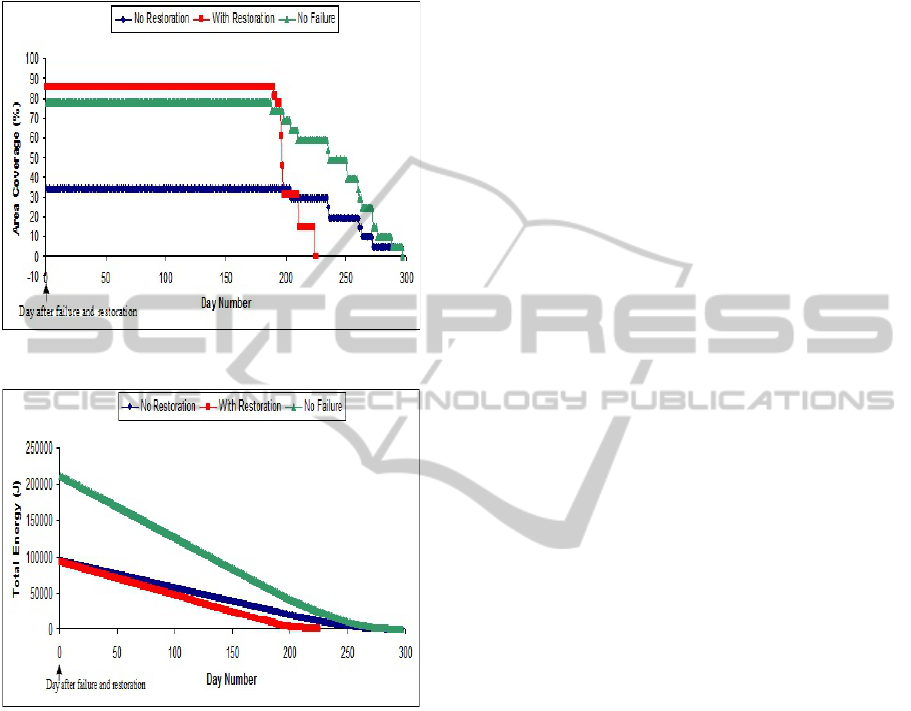
the restoration algorithm, the lifetime of the network

is reduced from 296 days to 223 days, which

corresponds to 24.6% reduction from the normal

lifetime of the network.

Figure 6: Comparison of coverage area.

Figure 7: Network energy level.

Figure 7 shows energy of the WSN in all the

three categories. The normal operation has higher

energy level than the network with failed sensors

(with and without restoration). The sensors failure

reduces the total energy level of the network from

approximately 200,000J to 100,000J. It is also

observed that the energy level of the network with

restoration is in-line with the energy level of the

network without restoration for the first 100 days

and then gap between the graph with and without

restoration increases with the increased energy

consumption by the doubled sensing radius.

7 CONCLUSIONS

In this paper, we have proposed a coverage

restoration algorithm, whereby clustering is followed

by restoration to restore the sensing area of

simultaneously failed sensors. The proposed

algorithm divides the failed sensors into groups of

four with their proximity and the algorithm exploits

the mobility of the sensor nodes to relocate and

cluster the failed sensor nodes and double the sensing

range of few active sensors to restore the coverage.

Experimental results indicate that the proposed

algorithm increases the coverage area to 86% from

34% (without restoration) at the expense of a small

reduction (24%) in the life time of the network.

REFERENCES

Habib, S., and Marimuthu, P. N., 2010. A Coverage

Restoration Scheme for Wireless Sensor Networks

within Simulated Annealing, Proceedings of the

Seventh International Conference on Wireless And

Optical Communications Networks, Colombo, Sri

Lanka.

Jia, J., Chen, J., Chang, G., Wen, Y., and Song, J., 2009.

Multi-objective Optimization for Coverage Control in

Wireless Sensor Network with Adjustable Sensing

Radius. Journal of Computers and Mathematics with

Applications, vol. 57, no. 11-12, pp. 1767-1775.

Wang, G., Cao, G., Porta, T., and Zhang, W., 2005. Sensor

Relocation in Mobile Sensor Networks. Proceedings

of IEEE Annual Joint Conference of the

Communications Societies, 2005, Miami, Florida,

USA.

SENSORNETS 2012 - International Conference on Sensor Networks