TRACKING-BY-REIDENTIFICATION IN A NON-OVERLAPPING

FIELDS OF VIEW CAMERAS NETWORK

Boris Meden

, Fr

eric Lerasle

2,3

, Patrick Sayd

and Christophe Gabard

CEA, LIST, Vision and Content Engineering Laboratory, Point Courrier 94, F-91191 Gif-sur-Yvette, France

CNRS, LAAS, 7 Avenue du Colonel Roche, F-31077 Toulouse Cedex 4, France

Universit

e de Toulouse, UPS, INSA, INP, ISAE, UT1, UTM, LAAS, F-31077 Toulouse Cedex 4, France

Keywords:

Reidentiﬁcation, Tracking, Camera Network, Non-overlapping Fields of View, Particle Filtering.

Abstract:

This article tackles the problem of automatic multi-pedestrian tracking in non-overlapping ﬁelds of view

camera networks, using monocular, uncalibrated cameras. Tracking is locally addressed by a Tracking-by-

Detection and reidentiﬁcation algorithm. We propose here to introduce the concept of global identity into a

multi-target tracking algorithm, qualifying people at the network level, to allow us to rebound observation dis-

continuities. We embed that identity into the tracking loop thanks to the mixed-state particle ﬁlter framework,

thus including it in the search space. Doing so, each tracker maintains a mutli-modality on the identity in

the network of its target. We increase the decision strength introducing a high level decision scheme which

integrates all the trackers hypothesis over all the cameras of the network with previous reidentiﬁcation results

and the topology of the network. The tracking and reidentiﬁcation module is ﬁrst tested with a single camera.

We then evaluate the whole framework on a 3 non-overlapping ﬁelds of view network with 7 identities. The

only a priori knowledge assumed is a topological map of the network.

1 INTRODUCTION

This article addresses the problem of pedestrian track-

ing in large scale environnment. Material and eco-

nomical reasons generally limit the number of cam-

eras thus yielding discontinuities/blind spot in the net-

work ﬁeld of view. We use the term non overlap-

ping ﬁelds of view networks (abbreviated NOFOV

networks). Figure 2 provides an example of such a

network.

The goal of the tracking module is then to cope

with these discontinuities and to still guarantee spatio-

temporal consistency. Beyond the image plane track-

ing, the system should be able to re-identify the tar-

gets when it appears in a new camera.

We propose here to integrate the reidentiﬁcation

mixed-state particle ﬁlter framework (Meden et al.,

2011) in a multi-target tracking-by-detection algo-

rithm (Breitenstein et al., 2010). This allows an online

reidentiﬁcation, embedded in the multi-target track-

ing process, based on a colorimetric signature of the

identities. The second contribution of that paper re-

sides in the addition of a supervision module, working

at the network level, that integrates and compares the

reidentiﬁcation results and validates them relatively to

the network topology.

Previous works are reviewed in the section 2.

Then, we describe the tracking-by-reidentiﬁcation

module, that operates on each camera in the section 3.

The supervision module is detailed in 4. Finally, sec-

tion 5 presents both qualitative and quantitative anal-

ysis of the camera level module, and of the addition

of topological constraints when applied to a NOFOV

network.

Figure 1 summarizes the proposed architecture,

with local treatments of the cameras and the centrali-

sation of the reidentiﬁcation results.

2 STATE OF THE ART

Pedestrian reidentiﬁcation becomes a necessity when

targets’ trajectories present discontinuities due to the

lack of observability. The underlying notion is the one

of global identity within the network, opposed to the

local identity of each tracker tracking locally a target

during its visibility time in the camera. The quality of

a multi-target tracking framework is evaluated by its

capacity to keep trackers on the targets they follow w-

Meden B., Lerasle F., Sayd P. and Gabard C..

TRACKING-BY-REIDENTIFICATION IN A NON-OVERLAPPING FIELDS OF VIEW CAMERAS NETWORK.

DOI: 10.5220/0003818300950103

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 95-103

ISBN: 978-989-8565-04-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

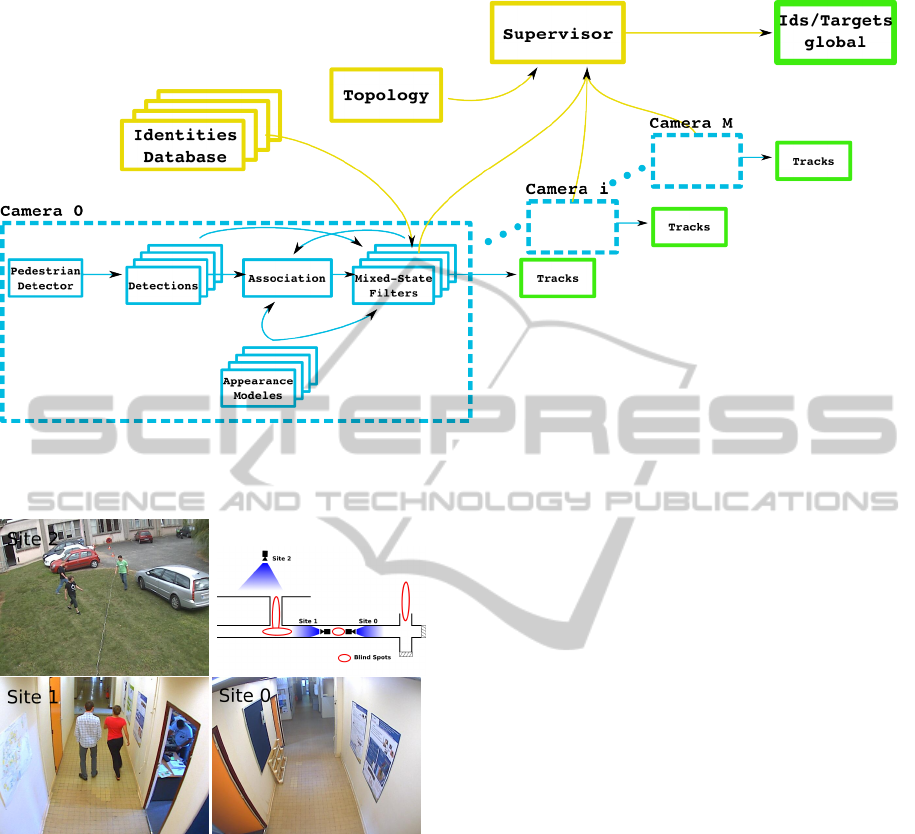
Figure 1: Achitecture of our system. Tracking and reidentiﬁcation in the image are localized at the cameras level, whereas

the supervisor works at the network level, confronting identities distributions between them and to the topology.

Figure 2: Camera network with non-overlapping ﬁelds of

views.

hile these targets are visible, i.e. to keep the same lo-

cal identity (Bernardin and Stiefelhagen, 2008). How-

ever this notion of identity is limited to the spatio-

temporal continuity of the tracking (after exiting, a

re-entering target would receive a new local identity).

The problem of joint tracking and identiﬁcation in

overlapping ﬁelds of view network e.g. (Qu et al.,

2007) is really similar. The combination of video

streams from different sensors comes usually with the

calibration of the system, allowing to work in com-

mon coordinates, and thus identiﬁcation is based on

the trackers spatio-temporal continuity.

However, a NOFOV network (ﬁgure 2) presents

discontinuous observations, corresponding to the tar-

gets’ transit times between the different cameras of

the network or to entry/exit within the same cam-

era. This problem is called pedestrian reidentiﬁcation,

and we introduce here the notion of global identity to

qualify a target in the network, which will be his/her

identity at each of his/her periods of observability in

the cameras.

This reidentiﬁcation problem is classically treated

as a request in a database, inspired from web tech-

nologies, and put the focus on the pedestrian ap-

pearance description to re-identify. Thus, (Gray and

Tao, 2008) propose to train a classiﬁer on the invari-

ant parts during a camera change. (Farenzena et al.,

2010) adopt the same approach whithout any learning,

proposing a robust ﬁxed signature based on symetry

and asymetry of the appearance and well positionned

colorimetric features. These methods are costly in

terms of computation time and are well suited to

a posteriori treatments.

For a camera network application, the reidentiﬁ-

cation module should allow real time computation of

video streams. Here we target an online update of tar-

gets’ global identities. A similar problem has been

tackled by (Chen et al., 2008; Lev-Tov and Moses,

2010; Zajdel and Kr

ose, 2005). However (Zajdel and

ose, 2005) suppose to have single pedestrians pass-

ing in the network, (Chen et al., 2008) do not report on

their tracking process and (Lev-Tov and Moses, 2010)

just simulate a NOFOV network and do not work on

images. These works do not consider tracking and

reidentiﬁcation jointly, and thus occult the difﬁculties

of multi-target tracking.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

Mono-camera multi-target tracking is a largely

tackled problem in the Computer Vision community:

our approach is based on different associated assess-

ments. First, particle ﬁltering algorithms’ interest

for tracking (CONDENSATION) have been established

since the initial work of Isard and Blake in (Isard

and Blake, 2001), notably for multiple targets. Then,

since (Okuma et al., 2004), tracking-by-detection has

emerged and particularly the temporal integration of

tracklets, which robustness has been proven by Kau-

cic et al. in (Kaucic et al., 2005). Tracklets optimisa-

tion has also been extended to two cameras present-

ing a disjoint ﬁeld of view by (Kuo et al., 2010). This

method yet does not work online, as the optimisation

is conducted on a temporal window.

In opposition to them, our approach places itself

in the markovian formalism for the tracking module.

Our approach is inspired of (Breitenstein et al., 2010)

and (Wojek et al., 2010). Like (Breitenstein et al.,

2010), it is based on distributed particle ﬁlters en-

hanced by a reidentiﬁcation component coming from

a discrete identity variable also sampled. They are

termed mixed-state particle ﬁlters. Then, in the vein

of (Wojek et al., 2010), we perform a tracklet tempo-

ral integration, but on the identities here, and not for

cameras but on the whole network.

3 TRACKING-BY-

REIDENTIFICATION WITHIN

A CAMERA

In this article, we propose an extension to NOFOV

networks of the tracking-by-detection algorithm pro-

posed by Breitenstein et al. in (Breitenstein et al.,

2010), introducing the notion of global identity that

we seek to retrieve for each target. We present in

this section our implementation of (Breitenstein et al.,

2010) and how the use of mixed-state particle ﬁltering

for reidentiﬁcation (Meden et al., 2011) comes to ex-

tend that approach.

3.1 Targets Description

3.1.1 Global Identities Learning

Each reidentiﬁcation algorithm needs a ﬁrst view be-

fore allowing any reidentiﬁcation. Here, we assume

that such a database is acquired ofﬂine. To do so,

we extract a collection of key-frames from one of the

cameras (e.g. positioned in the entrance hall of the

building to monitor), and we use these as description

of our global identities. The choice of the key-frames

is done with K-means on tracking sequences from the

chosen camera as detailled in (Meden et al., 2011).

Thus, these key-frames encode the variability of the

identity during its ﬁrst tracking. Figure 3 presents

the identity database used for the network of ﬁgure 2,

learned in camera 1.

Figure 3: Key-frames of each identity for the NOFOVNet-

work sequence (issued from camera 1).

3.1.2 Target Appearance Modelling

We use the same appearance model as depicted

in (Meden et al., 2011) to describe the targets and

their identities in the database: horizontal stripes of

color distributions, computed in the RGB space. The

similarity between two descriptors is the Bhattachar-

rya distances between corresponding stripes, normal-

ized by a gaussian kernel. This allows us to compute

similarities to the appearance model of a tracker, and

also to the key-frames of an identity in the database,

respectively noted w

App

(.) and w

(.).

3.2 Detections Integration

3.2.1 Association to Detections

Our approach favor a tracking-by-detection strategy

via the classical HOG detector proposed by Dalal and

Triggs in (Dalal and Triggs, 2005). These detections

are integrated in the tracking process by a greedy as-

sociation stage. After that association, each tracker

has potentially received a detection which will be

used to update the particles. To do so, an associa-

tion matrix is built between trackers and detections.

The score of pair detection d vs. tracker tr given by

equation (1), involves:

• the distance between the tracker’s particles and

the detection, evaluated under a gaussian kernel

(.) ∼ N (.,σ

) ;

• the tracker’s box area A(tr) relatively to the detec-

tion’s one also evaluated under a gaussian kernel;

• the tracker’s appearance model evaluated on the

detection (w

App

(.)).

S(d,tr) =

∑

p∈tr

(d − p)

| {z }

euclidean distance

× p



|A(tr) − A(d)|

A(tr)



| {z }

relative size

× w

App

(d,tr)

| {z }

appearance model

(1)

TRACKING-BY-REIDENTIFICATION IN A NON-OVERLAPPING FIELDS OF VIEW CAMERAS NETWORK

Thus, tracker and detection should present simulta-

neously a similar position, a similar size and a similar

colorimetric response. Once the matrix is built, max-

ima are extracted on greed manner, suppressing lines

and columns after affectation. The process is iterated

till the pairing threshold is reached. Such a heuris-

tic is preferred to the optimal method, the Hungarian

Method (Kuhn, 1955), unsuited for its complexity.

3.2.2 Automatic Tracker

Initialisations/Terminations

Every temporally recurrent detection, which is not as-

sociated to any tracker, yields the instanciation of a

new tracker. On a similar manner, every tracker which

has not been associated with a detection for a time pe-

riod longer than the suppression threshold is stopped.

3.3 Particle Filtering

3.3.1 Mixed-state Prediction Model

Each target initialized on a detection is tracked by a

particle ﬁlter. Given the identity database, we have

extra reference descriptors to compare with. To do

so, following (Meden et al., 2011), we use Mixed-

State CONDENSATION ﬁlters, introduced in (Isard

and Blake, 1998). We aim to estimate a mixte state

vector, composed of several continuous terms and a

discrete one.

X = (x,id)

, x ∈ R

, id ∈ {1, ... ,N

}

The continuous part of the state x = [x,y, v

]

composed of the position in the image plane (x,y)

and of the speed vector (v

)

. The integer part id

refers to one of the N

identities in the database. The

tracking is conducted in the image plane, and track-

ing box dimension is updated on the associated detec-

tions. The appearance model is also updated on the

associated detection. Given this extended state vec-

tor, the density of sampling process at image t can be

decomposed (Isard and Blake, 1998):

p(X

t−1

) = p(x

|id

t−1

) · P(id

t−1

)

P(id

t−1

) : P(id

= j|x

t−1

,id

t−1

= i) = T

i j

t−1

)

p(x

|id

t−1

) : p(x

t−1

,id

t−1

= i,id

= j) = p

i j

t−1

)

where T

i j

t−1

) is the transition probability from

identity i to j, applied to the discrete identity pa-

rameter, and p

i j

t−1

) is the sampling applied to

the continuous part. The transition matrix T = [T

i j

]

is built over the set of key-frames. The element T

i j

is the similarity w

(.) between identities i and j of

the database, computed between the most different

key-frames. Particles are propagated according to a

ﬁrst order motion model:

i j

t−1

) :



(x,y)

= (x,y)

t−1

+ (v

)

t−1

· ∆t +ε

(x,y)

)

= (v

)

t−1

+ ε

)

where the noises ε

(x,y)

and ε

(x,y)

are drawn from nor-

mal distribution and where ∆t is the time interval be-

tween two images.

3.3.2 Observation Model Integrating Detections

The weight w

(p)

associated with the p-th particle of

tracker tr is computed integrating the distance to the

associated detection d

∗

, the colorimetric similarity to

the appearance model w

App

(.) and the colorimetric

similarity to the identity of the particle w

(.). Id(p)

represents the identity taken by particle p. This is the

discrete parameter of p.

(p)

α · I (tr) · p

∗

− p)

| {z }

distance to the detection

+β · w

App

(d,tr)

| {z }

appearance model

+γ · w

(d,id(p))

| {z }

identity

(2)

where α, β and γ are weighting coefﬁcients, and I (tr)

is a boolean signifying the existence or not of an as-

sociated detection to the tracker. As in (Meden et al.,

2011), the introduction of similarity relative to the

identity in the particle weighting drives the particle

cloud towards the most likely identities given the re-

ceived observations. In that way, each tracker main-

tains a discrete distribution over the global identities,

the modes of that distribution being the most likely

identities.

The state estimation is a two-stage process. First

we compute the Maximum A Posteriori over the dis-

crete parameter relatively to the current observation

with equation (3), i.e. the most likely identity at

time step t.

= argmax

P(id

= j|Z

) = arg max

∑

p∈ϒ

(p)

(t), (3)

where ϒ

p|X

(p)

= (x

(p)

, j)

Then, the continuous components are estimated

over the subset of particles

ϒ which have that most

likely identity, following equation (4).

∑

p∈

(p)

(t) · x

(p)

∑

p∈

(p)

(t), (4)

where

ϒ = {p|X

(p)

= (x

(p)

)

}

That way, on top of target image position estima-

tion, each ﬁlter provides a discrete identity distribu-

tion for its target.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

4 TOPOLOGICO-TEMPORAL

SUPERVISION OF THE

REIDENTIFICATIONS

Section 3 has presented a reidentiﬁcation strategy in-

tegrated to the image plane tracking. That strategy has

been established as superior to an exhaustive compar-

ison to the database by (Meden et al., 2011). Its lim-

itation resides in the distributed aspect of the mixed-

state ﬁlters. Indeed, the probability densities over the

target identity are independent from one ﬁlter to an-

other. Thus, two ﬁlters may produce the same identity

at the same time for two different targets. We wish

here to constrain the process, so that it produces ex-

clusive trackers/identities pairing. This is done at the

network level.

4.1 Identities Tracklets Generation

4.1.1 Using the Topology

In this part, we suppose to have access to the topol-

ogy of the network we monitor. This topology is rep-

resented by a non-oriented graph G = (V,E), which

vertices V represent entry/exit areas in the cameras,

and which edges E give existing transitions between

these areas, as illustrated in ﬁgure 4.

This ﬁxed a priori here, could be learned online

with methods such as (Chen et al., 2008).

Figure 4: Network topology modelling. A non-oriented

graph link entry/exit areas of the adjacent cameras.

4.1.2 Temporal Integration

Each tracker produces at each time step a discrete

probability distribution over the set of identities, com-

puted as the ratio of particles dedicated to one iden-

tity. These probabilities are aggragated over a time

window in a Dynamic Programming manner. Fol-

lowing (Wojek et al., 2010), we speak here of track-

lets over the identities. Doing so, we build an asso-

ciation matrix between trackers and identities using

equation (5).

The use of the network topology comes in at

that point. It is used to suppress the impossible

tracker/identity associations. We start from an initial

localization of the identities in the network. At every

termination of a tracker, this localization is updated

with its reidentiﬁcation. We use that localization to

set to null the associations that violate this localiza-

tion. An association is violating it if the tracker’s area

is not connected to the last localization of the pro-

posed identity.

S(tr

,id

) = p (id

|zone(tr

)) ·

∏

t=t

Card



tr,id



(5)

o ϒ

tr,id

p|X

(p)

= (x

(p)

,id

)

and where

p(id|zone(tr)) =



1 si localization[id]=zone(tr) ;

0 sinon.

4.1.3 Association Exclusivity

A greedy exclusive association similar to the one de-

scribed in section 3, is performed. It works using the

similarity function (5) and produces and exclusive as-

sociation tracker/identity at the end of the time win-

dow. The topology, and the preceding reidentiﬁcation

come to suppress impossible conﬁguration. Finally,

the association forces exclusivity in the pairing.

The management of the global identities at the

core of the tracking process allows us to skip combi-

natory problems inherent when handling multiple tar-

gets and to maintain up-to-date the positions of these

identities in the network.

4.2 Tracklets Optimisation over a

Tracking Sequence

These supervised affectations come at the end of each

time window, and give the re-identiﬁcation during the

next time window. We obtain here short period re-

identiﬁcations, which we call identity tracklets. Fig-

ure 5 presents different tracklets of identities infered

by the supervisor for a tracking sequence. Each color

refers to an identity in the database.

To avoid a reidentiﬁcation process biased on the

begining of the tracking sequence, we settle the iden-

tity distribution in the mixed-state ﬁlters back to

equiprobability at the end of each time window. That

TRACKING-BY-REIDENTIFICATION IN A NON-OVERLAPPING FIELDS OF VIEW CAMERAS NETWORK

Figure 5: Different identity tracklets during a tracking se-

quence (better viewed in colors).

way, the mixed-state reidentiﬁcation ﬁlter explores

again each identity and converge towards the most

likely, relatively to the observations it receives.

For each active tracker, these reidentiﬁcations are

binned into an histogram indexed over the identities.

Following Dynamic Programming principles, the cur-

rent affectation trackers / identities displayed is the

best solution found so far, i.e.the strongest mode of

that histogram. In the same way, when a tracker is

stopped, the re-identication affected is the strongest

mode, and the localization in the topological graph of

that identity is updated.

5 IMPLEMENTATION AND

ASSOCIATED EVALUATIONS

5.1 Implementation

Our IP network has an average framerate of 16 im-

ages per second. We thus ﬁx ∆t = 1/16s in the evolu-

tion model of the particles ﬁlters. In the observation

model, equation (2), we ﬁx empirically:











α = 0.90, β = 0.05 and γ = 0.05 if I (tr) = 1

(Breitenstein et al., 2010)

α = 0.0, β = 0.8 and γ = 0.2 else,

(Meden et al., 2011).

In the supervisor, the time window length is set to 7

images, which correspond to the average convergence

time of the mixed-state ﬁlters towards their identity.

5.2 Evaluations

5.2.1 Datasets

We evaluate the different component of our approach

on two different datasets. First, we test the tracking

module without and with reidentiﬁcation activated on

the sequence PETS’09 S2L1

. This public dataset,

composed of 795 frames, presents an open outdoor

area, where 10 pedestrians wander, with crossings and

enterings/exitings. Having labeled these data, we are

able to quantify the quality of our tracking algorithm.

Considering the lack of public datasets in terms

of NOFOV network, we evaluate the supervision part

on a private sequence which we call the NOFOVNet-

work sequence in the sequel. It presents a total of

7 pedestrians wandering between 3 cameras. There

is no overlapping between the cameras ﬁeld of view.

Two of them are placed in a building corridor, the

third one monitoring an outside area with a conﬁgura-

tion similar to PETS’09. The dataset has 837 frames.

We plan to release publicly these data.

5.2.2 Metrics

We use the CLEAR MOT (Bernardin and Stiefelha-

gen, 2008) to quantify tracking results. We obtain

a precision score MOTP (Multiple-Object Tracking

Precision) computed as the intersection over the union

between tracking boxes and ground truth, and an ac-

curacy score MOTA (Multiple-Object Tracking Ac-

curacy) taking into account false positives, false neg-

atives and switching trackers between targets.

Moreover, we evaluate the reidentiﬁcation perfor-

mances by a True Reidentiﬁcation Rate (TRR), com-

puted as the ratio of correct reidentiﬁcation over the

number of trials. Given that the supervisor operates

on a time window, these TRRs are updated only at the

end of these time windows.

5.3 Camera Level Performances

5.3.1 Global Identity Notion

Figure 6: Key-frames of the 10 identities in the PETS se-

quence.

Figure 6 gives an overview of the identity database

we used on the sequence PETS’09. Here there is

only one camera. Thus, the database images are taken

from the test sequence. The goal here is to illus-

trate the tracking-by-reidentiﬁcation, compare its per-

formances without reidentiﬁcation and highlights the

new modality it offers.

http://www.cvg.rdg.ac.uk/PETS2009/a.html

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

100

(a) (b)

Figure 7: Results from (Breitenstein et al., 2010) (a) Be-

tween frames 204 and 241 the highlighted person exit and

enter again the scene. The new tracker is matched with the

old trajectory on a spatial criterion. (b) A similar situation

happens between images 390 and 445. However that time, it

is a different person who enters. The new tracker is matched

again with the previous trajectory. Here this is a reidentiﬁ-

cation failure as the person is different.

Figure 8: Interest of using reidentiﬁcation embedded in the

multi-target tracking: in (a) as like as in (b), the system re-

identiﬁes the target relatively to the identity database, and

detects that in (b) the person entering is not the same as the

exiting one.

Figures 7 and 8 illustrate the limitation of han-

dling only local identities when targets exit and then

re-enter the scene. On ﬁgure 7, when the person exits

and a new one enters, the trajectory of the preceding is

matched with the new one. (Breitenstein et al., 2010)

just use a simple spatial criterion, no reidentiﬁcation

is involved in that matching. It works on ﬁgure 7(a)

as the person is the same, but not on ﬁgure 7(b) as the

person is different.

In our case (ﬁgure 8), at each time step, each

tracker provides a probability distribution for the

observed identity. This allows us to tolerate peri-

ods without observations like exits from the camera.

When the target re-enter, the tracker searches again

the correct identity.

5.3.2 Quantitative Analysis

Table 1 presents quantitative results on the PETS’09

sequence. First, we validate our partial implemen-

tation of (Breitenstein et al., 2010) (without HOG +

ISM detector, detector conﬁdence use in the obser-

vation model, and Boosting Online based appearance

model).

However, our approach presents an extra modal-

ity with the notion of global identity. We show ﬁrst

that the introduction of mixed-state particle ﬁltering

does not decrease much tracking performances. To

do so, we compare MOTP and MOTA for our imple-

mentation without and with the reidentiﬁcation mod-

ule activated. Then, this extra modality allow us to

compute TRR for the sequence. Finally, we compare

the reidentiﬁcation results of the distributed mixed-

state ﬁlters alone against the supervised ones. There,

exclusivity constraints (section 4) yield improved re-

sults.

The stochastic aspect of particle ﬁltering has been

taken into account in our experiences: table 1 shows

results averaged over ten repetitions of tracking.

Table 1: CLEAR MOT metrics tracking results (Bernardin

and Stiefelhagen, 2008) and true reidentiﬁcation rates on

the monocamera sequence PETS’09 S2L1. We give here

Multi-Object Tracking Precision (MOTP), Multi-Object

Tracking Accuracy (MOTA), and True Reidentiﬁcation

Rate (TRR) deﬁned in section 5.2.

Sequence PETS’09 MOTP MOTA TRR

Tracking-by-detection 56.3% 79.7% -

(Breitenstein et al., 2010)

Tracking-by-detection 42.7% 77.9% -

implemented

Tracking-by-Reidentiﬁcation 42.5% 77.7% 59.7%

Tracking-by-Reidentiﬁcation 42.4% 75.9% 64%

supervised

5.4 Supervisor Performances

The NOFOVNetwork sequence being not annotated

for the tracking, we just present true reidentiﬁcation

rates for that sequence. We compare here the method

based only on colorimetric information and particle

TRACKING-BY-REIDENTIFICATION IN A NON-OVERLAPPING FIELDS OF VIEW CAMERAS NETWORK

101

Figure 9: Network tracking example: output of our system with camera tracks matched to global identities (left), allowing to

localize them in the topology (right).

ﬁltering inspired by (Meden et al., 2011), with the su-

pervised system we propose in section 4 which in-

cludes exclusivity and topological constraints.

Table 2 presents true reidentiﬁcation rates per

camera, and for the whole network. The database be-

ing built with descriptors taken from camera 1, this

explains better TRR in that camera. These results il-

lustrate the contribution of the supervisor. Each cor-

rectly re-identiﬁed target constrains the system in the

sequel through the topology.

Table 2: True Reidentiﬁcation Rates for each camera of the

sequence NOFOVNetwork: comparison of the approaches

without, and with supervisor on the network.

NOFOV Sequence cam0 cam1 cam2 network

Tracking-by-Reidentiﬁcation 43.7% 67.3% 55.5% 54.6%

Tracking-by-Reidentiﬁcation 67.7% 76.9% 63.8% 68.2%

supervised

Finally, ﬁgure 9 gives an overview of our system

output. Left, the cameras of the network display cur-

rent tracks, and right, the identities are localized in the

topology.

6 CONCLUSIONS

This article deals with non-overlapping ﬁelds of view

cameras networks monitoring, aiming at localizing

the targets in the topology. This is achieved through

the concept of global identity. We present here a

two stage tracking-by-reidentiﬁcation method, based

respectively on colorimetric signatures and spatio-

temporal constraints in the network.

The camera level is treated by a markovian

tracking-by-detection inspired by (Breitenstein et al.,

2010), enhanced by the concept of global identity

taken into account in the mixed-state particle ﬁlter

framework. Thus, each tracker builds a discrete iden-

tity distribution for its target. Doing so, it integrates a

re-initialisation capacity after the target’s exit.

These identity distributions, considered as track-

lets over the identities are ﬁltered spatio-temporally

by a supervisor. This one forces exclusivity between

reidentiﬁcations and insure consistency regarding the

network topology.

A ﬁrst extension resides in the database online

learning and updating to achieve a fully automatic

system. Further work will also investigate a more en-

hanced appearance model, e.g. trained online on its

target. Finally, additional knowledge about the scene

(e.g., a ground plane to improve targets size estima-

tion) would be beneﬁcial.

REFERENCES

Bernardin, K. and Stiefelhagen, R. (2008). Evaluating mul-

tiple object tracking performance: the clear mot met-

rics. Journal on Image and Video Processing.

Breitenstein, M., Reichlin, F., Leibe, B., Koller-Meier,

E., and Van Gool, L. (2010). Online multi-

person tracking-by-detection from a single, uncali-

brated camera. Pattern Analysis and Machine Intel-

ligence.

Chen, K., Lai, C., Hung, Y., and Chen, C. (2008). An adap-

tive learning method for target tracking across multi-

ple cameras. In Int. Conf. on Computer Vision and

Pattern Recognition.

Dalal, N. and Triggs, B. (2005). Histograms of oriented gra-

dients for human detection. In Int. Conf. on Computer

Vision and Pattern Recognition.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

102

Farenzena, M., Bazzani, L., Perina, A., Murino, V., and

Cristani, M. (2010). Person re-identiﬁcation by

symmetry-driven accumulation of local features. In

Int. Conf. on Computer Vision and Pattern Recogni-

tion.

Gray, D. and Tao, H. (2008). Viewpoint invariant pedestrian

recognition with an ensemble of localized features. In

Europ. Conf. on Computer Vision.

Isard, M. and Blake, A. (1998). A mixed-state CONDEN-

SATION tracker with automatic model-switching. In

Int. Conf. on Computer Vision.

Isard, M. and Blake, A. (2001). BraMBLe: a Bayesian mul-

tiple blob tracker. In Int. Conf. on Computer Vision.

Kaucic, R., Perera, A., Brooksby, G., Kaufhold, J., and

Hoogs, A. (2005). A uniﬁed framework for tracking

through occlusions and accross sensor gaps. In Int.

Conf. on Computer Vision and Pattern Recognition.

Kuhn, H. (1955). The hungarian method for the assignment

problem. Naval research logistics quarterly.

Kuo, C., Huang, C., and Nevatia, R. (2010). Inter-camera

association of multi-target tracks by on-line learned

appearance afﬁnity models. In Europ. Conf. on Com-

puter Vision.

Lev-Tov, A. and Moses, Y. (2010). Path recovery of a dis-

appearing target in a large network of cameras. In Int.

Conf. on Distributed Smart Cameras.

Meden, B., Sayd, P., and Lerasle, F. (2011). Mixed-State

Particle Filtering for Simultaneous Tracking and Re-

Identiﬁcation in Non-Overlapping Camera Networks.

In Scandinavian Conference on Image Analysis.

Okuma, K., Taleghani, A., De Freitas, N., Little, J., and

Lowe, D. (2004). A boosted particle ﬁlter: multitarget

detection and tracking. In Europ. Conf. on Computer

Vision.

Qu, W., Schonfeld, D., and Mohamed, M. (2007). Dis-

tributed bayesian multiple-target tracking in crowded

environments using multiple collaborative cameras.

Int. Journal EURASIP.

Wojek, C., Roth, S., Schindler, K., and Schiele, B. (2010).

Monocular 3D scene modeling and inferences: under-

standing multi-object trafﬁc scenes. In Europ. Conf.

on Computer Vision.

Zajdel, W. and Kr

ose, B. (2005). A sequential bayesian

algorithm for surveillance with nonoverlapping cam-

eras. Int. Journal of Pattern Recognition and Artiﬁcial

Intelligence.

TRACKING-BY-REIDENTIFICATION IN A NON-OVERLAPPING FIELDS OF VIEW CAMERAS NETWORK

103