
CODED APERTURE STEREO
For Extension of Depth of Field and Refocusing
Yuichi Takeda
1
, Shnisaku Hiura
2
and Kosuke Sato
1
1
Graduate School of Engineering Science, Osaka University, 1-3 Machikaneyama-cho, Toyonaka, 560-8531 Osaka, Japan
2
Graduate School of Information Sciences, Hiroshima City University, Ozuka-Higashi, Asa-Minami-Ku, 731-3194
Hiroshima, Japan
Keywords:
Computational Photography, Coded Aperture, Stereo Depth Estimation, Deblur, Depth of Field, Refocusing.
Abstract:
Image acquisition techniques using coded apertures have been intensively investigated to improve the perfor-
mance of image deblurring and depth estimation. Generally, estimation of the scene depth is a key issue in the
recovery of optical blur because the size of the blur kernel varies according to the depth. However, since it is
hard to estimate the depth of a scene with a single image, most successful methods use several images with
different optical parameters captured by a specially developed camera with expensive internal optics. On the
other hand, a stereo camera configuration is widely used to obtain the depth map of a scene. Therefore, in this
paper, we propose a method for deblurring and depth estimation using a stereo camera with coded apertures.
Our system configuration offers several advantages. First, coded apertures make not only deconvolution but
also stereo matching very robust, because the loss of high spatial frequency domain information in the blurred
image is well suppressed. Second, the size of the blur kernel is linear with the disparity of the stereo images,
making calibration of the system very easy. The proof of this linearity is given in this paper together with
several experimental results showing the advantages of our method.
1 INTRODUCTION
Optical blur (defocusing) and motion blur are typical
errors in photographs taken in dark environments. If
the aperture of the lens is stopped down to extend the
depth of field, moving objects are likely to be blurred
with a slow shutter speed to keep the exposure value
constant. In other words, insufficient light from the
scene causes a trade-off between depth of field and
exposure time, and thus it is difficult to take a clear
sharp picture of a moving object in a dark scene using
a hand-held camera. Consequently, post processing of
captured images including deblurring and denoising,
have been intensively studied in prior years. In this
paper, we propose a method that extends the depth
of field computationally using a stereo camera with
coded apertures.
Typically, the performance of deblurring depends
on the knowledge about the point spread function
(PSF). If the shape of the PSF is not known, it should
be estimated during deconvolution. This technique,
called blind deconvolution, is generally an ill-posed
problem when dealing with only a single image, and
some kind of priors about the scene must be introdu-
ced(Levin et al., 2007). However, if the prior is not
suitable for the scene, simultaneous estimation of the
PSF and latent image will fail. Therefore, multiple
images with different optical parameters such as fo-
cus distance or aperture shape are commonly used
to make the problem solvable(Hiura and Matsuyama,
1998; Zhou et al., 2009). In this paper, we explore the
use of disparity introduced by a stereo camera pair to
determine the size of the PSF. Contrary to sequential
capture with different optical settings, stereo cameras
can deal with moving scenes. To determine the size
of the PSF, we need to calibrate the relationship be-
tween disparity and focus. In this paper, we present a
proof showing that the diameter of the blur kernel is
directly proportional to the relative disparity from the
focus distance.
The other important factor in the preciseness of
deblurring is the characteristics of the PSF. If a nor-
mal circular aperture is used, information in the high
spatial frequency domain is almost lost (Veeraragha-
van et al., 2007). Therefore, we introduce coded aper-
tures to two lenses of the stereo camera to retain the
information of the scene as far as possible. The spe-
cial aperture also makes the stereo matching robust,
103
Takeda Y., Hiura S. and Sato K..
CODED APERTURE STEREO - For Extension of Depth of Field and Refocusing.
DOI: 10.5220/0003818801030111
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 103-111
ISBN: 978-989-8565-03-7
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
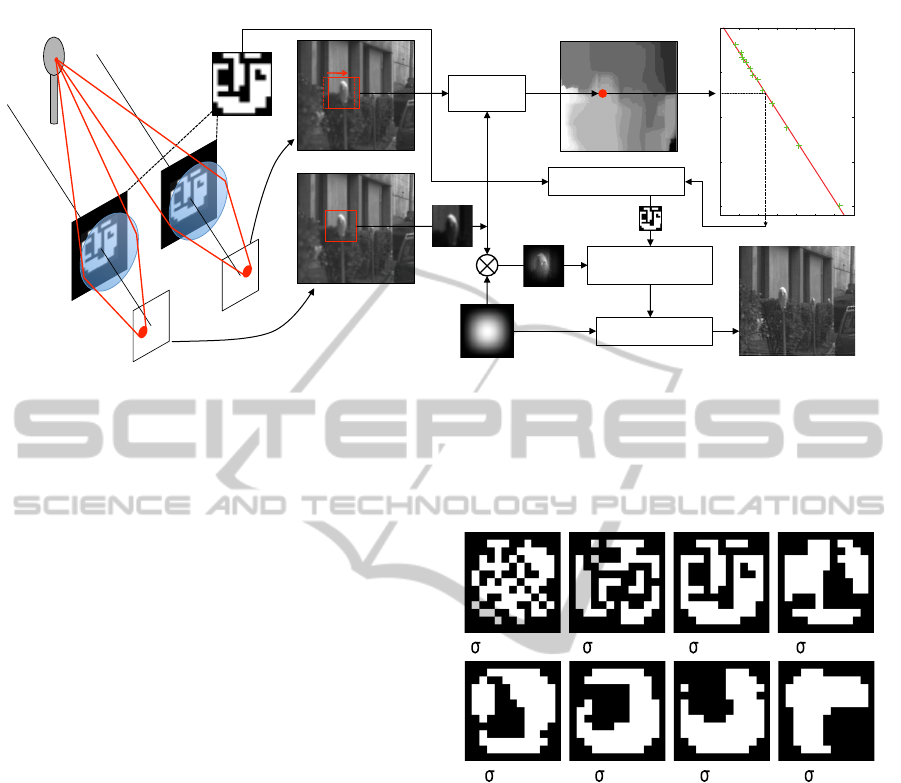
Left input image!
Right input image!
Disparity!
Stereo
Matching
Disparity Map!
All-in-focus Image!
Window Function!
Scaling of Blur Kernel
Wiener
Deconvolution
Integration!
(weighted sum)
Aperture
Pattern!
0
20
40
60
80
100
120
140
0 50 100 150 200
kernel size [pixel]
disparity [pixel]
Conversion of Disparity
to Blur Kernel Size
Coded
Apertures
Lens
Image
Sensors
Object
Figure 1: Process flow of proposed method.
and the clear scene is stably recovered using the pre-
cisely determined PSF.
Related work is briefly summarized in Section 2.
An overview of the proposed system and the algo-
rithms is presented in Section 3, together with a proof
of the linear relationship between blur size and dis-
parity. Experiments are discussed in Section 4, while
Section 5 concludes the paper.
2 RELATED WORK
Optical blur (defocus) appearing in images captured
with conventional cameras is modeled as the convo-
lution of the sharp original scene and a blur kernel
(i.e., the PSF). Thus, the latent image can be recon-
structed by applying an inverse filter or deconvolution
techniques to the captured image. Several methods
including Richardson-Lucy deconvolution (Richard-
son, 1972) and MAP estimation (Lam and Goodman,
2000) have been proposed; however, the performance
of the reconstruction depends greatly on the correct-
ness of the blur kernel. In particular, a circular blur
kernel in a conventional aperture contains many zero
crossings in the spatial frequency, while reconstruc-
tion at a frequency of low gain is unstable with much
noise influence. Therefore, the idea of designing an
aperture shape with the desirable spatial frequency
characteristics was proposed. Hiura et al. introduced
a coded aperture to improve the preciseness of depth
estimation using the defocus phenomenon (Hiura and
Matsuyama, 1998). Similarly, Levin et al. (Levin
et al., 2007) and Veeraraghavan et al. (Veeraraghavan
et al., 2007) tried to remove the defocus effect from
a single image taken by a camera with independently
designed coded apertures. Desirable aperture shapes
have been explored by Zhou et al. (Zhou and Nayar,
2009) and Levin et al. (Levin, 2010).
Circular Annular
MURA
Image Pattern
Random
Multi-Annular
Levin
Veeraraghavan
=0.0001
=0.001
=0.008 =0.01
=0.005=0.002
=0.02 =0.03
Proposed
Figure 3. All the aperture patterns we used in our simulations.
Top two rows: Eight patterns, including circular, annular, multi-
annular, random, MURA, image pattern, Levin et al.’s pattern [13],
and Veeraraghavan et al.’s pattern [3]. Bottom two rows: Eight of
our patterns optimized for noise levels from σ =0.0001 to 0.03.
have used it in all of our comparisons and experiments. It
must be noted that similar algorithms have been advocated
in the past (see [19] for example).
6. Performance Comparison of Apertures
Before conducting real experiments, we first performed
extensive simulations to verify our aperture evaluation cri-
terion and optimization algorithm. For this, we used the 16
aperture patterns shown in Figure 3. The top 8 patterns in-
clude simple ones (circular, annular, and multi-annular) and
more complex ones proposed by other researchers [9], [13],
[3]. In addition, we have tested an “image pattern,” which
is a binarized version of the well-known Lena image, and
a random binary pattern. The bottom 8 patterns were pro-
duced by our optimization algorithm for different levels of
image noise. The performances of these 16 apertures were
evaluated via simulation over a set of 10 natural images at
eight levels of image noise.
For each aperture pattern k and each level of image noise
σ, we simulated the defocus process using Equation (1), ap-
plied defocus deblurring using Equation (13), and got an
estimate
ˆ
f
0
of the focused image f
0
. Using each deblurred
image, the quality of the aperture pattern was measured as
�
�f
0
−
ˆ
f
0
�
2
. To make this measurement more reliable, we
repeated the simulation on 10 natural images and took the
average. These results are listed in Table 2 for the 16 aper-
ture patterns and 8 levels of image noise. Our optimized
patterns perform best across all levels of noise, and the im-
provement is more significant when the noise level is low.
On the other hand, the circular (conventional) aperture is
close to optimal when the noise level is very high. While
there are different optimal apertures for different levels of
image noise, we may want a single aperture to use in a va-
riety of imaging conditions. In this case, we could pick the
optimized pattern for σ =0.001 as it performed well over a
wide range of noise levels (from σ =0.0001 to 0.01).
It is interesting to note that the image pattern (Lena)
also produces deblurring results of fairly high quality. We
believe this is because the power spectrum of the image
pattern follows the 1/f law–it successfully avoids zero-
crossings and, at the same time, has a heavy tail covering the
high frequencies. Unfortunately, the image pattern consists
of a lot of small features, which introduce strong diffraction
effects. We believe that it is for this reason that the image
pattern did not achieve as high quality results in our experi-
ments as predicted by our simulations.
7. Experiments with Real Apertures
As shown in Figure 4(a), we printed our optimized aper-
ture patterns as well as several other patterns as a single high
resolution (1 micron) photomask sheet. To experiment with
a specific aperture pattern, we cut it out of the photomask
sheet and inserted it into a Canon EF 50mm f/1.8 lens
1
.
In Figure 4(b), we show 4 lenses with different apertures
(image pattern, Levin et al.’s pattern, Veeraraghavan et al’s
pattern, and one of our optimized patterns) inserted in them,
and one unmodified (circular aperture) lens. Images of real
scenes were captured by attaching these lenses to a Canon
EOS 20D camera. As previously mentioned, we choose the
pattern which is optimized for σ =0.001, as it performs
well over a wide range of noise levels in the simulation.
To calibrate the true PSF of each of the 5 apertures, the
camera focus was set to 1.0m; a planar array of point light
sources was moved from 1.0m to 2.0m with 10cm incre-
ments; and an image was captured for each position. Each
defocused image of a point source was deconvolved using
a registered focused image of the source. This gave us PSF
estimates for each depth (source plane position) and several
locations in the image
2
. In Figure 4(c-g), two calibrated
PSFs (for depths of 120cm and 150cm) are shown for each
pattern.
7.1. Comparison Results using Test Scenes
In our first experiment, we placed a CZP resolution chart
at a distance of 150cm from the lens, and captured images
using the five different apertures. To be fair, the same expo-
sure time was used for all the acquisitions. The five captured
images and their corresponding deblurred results are shown
1
We chose this lens for its high quality and because we were able to
disassemble it to insert aperture patterns with relative ease.
2
We measured the PSF at different image locations to account for the
fact that virtually any lens (even with a circular aperture) produces a spa-
tially varying PSF.
5
Figure 2: Shapes of Zhou’s codes for various noise levels,
σ (Zhou and Nayar, 2009).
Since the size of the blur kernel varies with the
distance between the camera and object, it is neces-
sary to estimate the depth of the captured scene accu-
rately. Depth estimation through the optical defocus
effect is called Depth from Defocus, and a number of
studies on this aspect have been carried out (Schech-
ner and Kiryati, 2000). In general, it is not easy to
estimate the depth of a scene using a single image, be-
cause simultaneous estimation of the blur kernel and
latent image is under constrained. Therefore, Levin et
al. (Levin et al., 2007) assumed a Gaussian prior to
the edge power histogram to make the problem well-
conditioned. However, this method is not always ro-
bust, and the authors mentioned that human assistance
was sometimes necessary.
Several studies estimating depth from multiple
images captured by different optical parameters have
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
104
been conducted to make Depth from Defocus robust.
Nayer et al. (Nayar et al., 1995) proposed a method
that captures two images with different focus dis-
tances from the same viewpoint by inserting a prism
between a lens and image sensor. Similarly, Hiura et
al. (Hiura and Matsuyama, 1998) used a multi-focus
camera that captures three images with different focus
distances, and introduced a coded aperture to simulta-
neously estimate the depth map and a blur-free image
of the scene using an inverse filter.
Figure 3: Log of the power spectrum of the aperture shape:
(left) the conventional iris diaphragm; (right) Zhoufs code
as used in this paper.
p
1
p
2
l
a
1
a
2
b
2
b
1
c
d
d
2
d
1
D
q
1
q
2
I
L
I
R
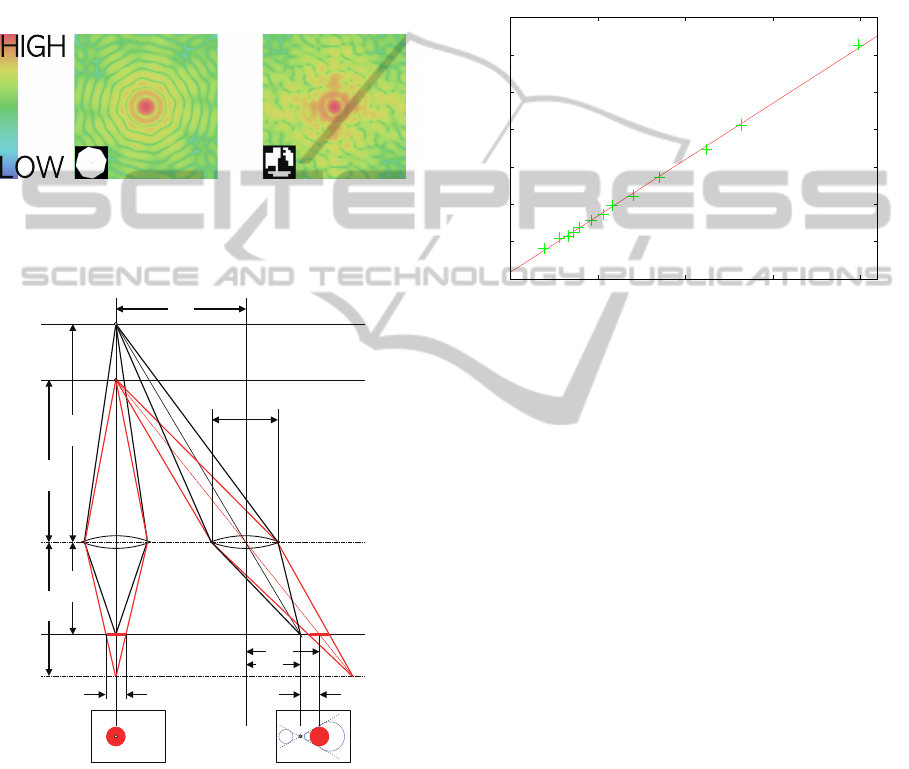
Figure 4: Relation between disparity and blur size.
Similarly, other optical factors can be incorpo-
rated to make the deblurring problem solvable. In the
research by Zhou et al. (Zhou et al., 2009), two dif-
ferent aperture shapes were used to estimate the depth
map and latent image. The authors also proposed op-
timal aperture shapes for their system, where the cen-
troid of the opening is offset from the center of the
aperture. This means that the difference in aperture
shapes occasionally has the effect of disparity, which
is commonly used in stereo cameras. However, accu-
racy of the depth estimation of Depth from Defocus is
lower than that of stereo depth estimation as pointed
out by Schechner et al. (Schechner and Kiryati, 2000)
because the disparity caused by the change in aperture
shape is limited to within the lens diameter. Addition-
ally, their system cannot deal with moving scenes be-
cause images with different aperture shapes are cap-
tured sequentially.
0
20
40
60
80
100
120
140
0 50 100 150 200
kernel size [pixel]
disparity [pixel]
Figure 5: Relation between disparity and blur kernel size.
Blur kernel size is linear with disparity. The red line denotes
the calibrated parameters.
To summarize, there are two methods for captur-
ing multiple images from a single lens with varying
optical parameters. In the first, an optical device such
as a prism or mirror is placed between the lens and im-
age sensor (Green et al., 2007), while in the other, im-
ages are captured sequentially with changing param-
eters (Liang et al., 2008). The former method is ex-
pensive and complicated with specially made optics,
while the latter is not applicable to moving scenes.
Additionally, using a single lens limits the precise-
ness of the depth estimation to a short baseline length
within the lens aperture. Therefore, we propose a ro-
bust depth estimation and deblurring method using
images captured by a stereo camera with coded aper-
tures. Stereo depth estimation is widely used since it
is not necessary to use special optical devices in the
camera. Furthermore, a stereo camera makes it pos-
sible to control the baseline length, which is indepen-
dent of the blur size of the lens, thus leading to robust
depth estimation. Coded apertures make not only de-
convolution but also stereo matching very robust, be-
cause the loss of high spatial frequency domain in-
formation in blurred image is adequately suppressed.
Calibration of the system is very easy because the size
of the blur kernel is linear with the disparity of stereo
images.
CODED APERTURE STEREO - For Extension of Depth of Field and Refocusing
105
(a) Circular aperture. (b) Coded aperture.
Figure 6: Captured images for the first experiment. Focus
was set at the nearest point (lower part of figures).
3 CODED APERTURE STEREO
An overview of our system and proposed method is
illustrated in Figure 1. Input images are captured by a
stereo camera with coded apertures. The shape of the
aperture is the same, and therefore, the effect of the
defocus is common to both input images.
First, stereo matching is calculated for the two
captured images, providing a depth map of the scene.
Any stereo matching algorithm for normal stereo
cameras without coded apertures can be used, because
the input images defocused by common coded aper-
tures are still identical at any distance.
Next, the input image is deblurred by applying
Wiener deconvolution. Since the size of the blur ker-
nel (diameter of circle of confusion) depends on the
distance to the object, disparity of the stereo matching
is used to calculate the size of the blur kernel. Since
0
2
4
6
8
10
12
0 1 2 3 4 5 6 7 8 9
error ratio[%]
variance
Coded Aperture
Conventional Aperture
Figure 7: Experiment 1: comparison of error ratio in stereo
matching.
Figure 8: Experiment 2: disparity map with coded aperture,
where a high intensity denotes a large disparity.
the scene consists of various distances, the input im-
age is clipped to many overlapping small regions us-
ing a window function. The final result of the whole
deblurred image is created by integrating all clipped
regions using a weighted average of the window func-
tion.
In this section, we first discuss the improvement
in depth estimation using a coded aperture. Then, we
show that the disparity of stereo matching is linear
with the size of the blur kernel.
3.1 Effect of a Coded Aperture on
Stereo Matching
Since the scene to be measured by the stereo cam-
era has various depths, input images are inevitably
affected by the optical blur phenomenon caused by
lenses focused at a fixed depth. In general, such
blurring effect degrades the accuracy of stereo depth
measurement, so the aperture of the lens is usually
stopped down as much as possible to extend the depth
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
106

of field. However, as described before, this decreases
the amount of light passing through the lens, and the
longer exposure time introduces motion blur. There-
fore, we propose coded aperture stereo, that is, stereo
depth measurement using images captured with a
coded aperture inserted in the lenses.
Since a coded aperture changes the shape of the
blur kernel, it is able to control the effect of opti-
cal blur to the desirable characteristics. From the
viewpoint of a spatial frequency domain, the high fre-
quency component of the scene texture should be kept
to make the stereo matching robust. This is the rea-
son that we use pan-focus settings for the stereo cam-
eras. For example, the blur kernel of an extremely
small aperture can be assumed to be a delta function,
which is considered to be one of the broadband sig-
nals. However, the transmission ratio inside the lens
aperture is less than 1, so the exposure value decreases
if we use small apertures. Therefore, we use a spe-
cially designed aperture to keep the high spatial fre-
quency component with a sufficient amount of light
using a coded aperture.
Several aperture shapes have been proposed in
various studies on coded apertures (Levin et al., 2007;
Veeraraghavan et al., 2007). In particular, Zhou et
al. (Zhou and Nayar, 2009) tried to find an optimal
aperture shape for the given signal-to-noise ratio of
the sensor. Henceforth, this code is referred to as
Zhou’s code. A genetic algorithm was used to find
Zhou code that is optimal for Wiener deconvolution
under the condition of a 1/ f distribution of the spa-
tial frequency for the scene as a prior. The final result
varies according to the noise level σ of the sensors as
shown in Figure 2.
Figure 3 shows the spatial frequency response of
the convolution using both circular and Zhou code
aperture shapes. A conventional aperture has periodi-
cal low values even at low spatial frequency (near the
center of the image), whereas even the high frequency
components are well kept with Zhou’s code. These
characteristics are expected to enhance the robustness
of the stereo matching like pan-focus settings as veri-
fied later through an experiment.
3.2 Disparity of Stereo Matching and
Circle of Confusion
In traditional studies on extending the depth of field
using a coded aperture (Hiura and Matsuyama, 1998;
Levin et al., 2007; Veeraraghavan et al., 2007; Zhou
et al., 2009; Levin, 2010), determining the size of the
blur kernel corresponds directly to the depth estima-
tion. In other words, the depth of a scene is estimated
through the recovery of the original images using a
deblurring technique. In our research, however, the
blur kernel must be independently estimated from the
disparity computed by the stereo matching. There-
fore, it is necessary to determine the relation between
disparity and blur size. In this subsection, we show
that the disparity in stereo measurement corresponds
linearly with the size of the circle of confusion.
Figure 4 depicts a stereo camera with optical axes
parallel with each other, and the two cameras having
lenses with the same diameter, D. Here, the optical
images of planes p
1
and p
2
are at planes q
1
and q
2
behind the lens, respectively. Without loss of gener-
ality, we can assume that the object is on the optical
axis of the left camera. The distances between the
lens and the four planes denoted by a
1
, a
2
, b
1
, and b
2
in Figure 4 have the following relationships with the
raw lenses:
1
a
1
+
1
b
1
=
1
a
2
+
1
b
2
=
1
f
(1)
where f is the common focal length of the lenses.
Then, we assume that two image sensors are
placed on plane q
1
, and an object on plane p
2
is out
of focus while the one on p
1
is in focus. Since the
two lenses have the same aperture shape, images of
the point on plane p
2
are observed as the same figures
on images I
L
and I
R
. In Figure 4, these are depicted as
red circles. Images of the points on planes p
1
and p
2
have disparities d
1
and d
2
, respectively. Using these
parameters, we can calculate the relative disparity, d,
from the focus distance as
d = d
2
− d
1
=
(
1
a
2
−
1
a
1
)
b
1
l (2)
where l is the length of the baseline of the stereo cam-
era.
Next, the diameter of the circle of confusion c for
the point on plane p
2
can be expressed as
c =
b
2
− b
1
b
2
D (3)
using the distance between q
1
and q
2
. Thus, using
Eqs. (2) and (3), we can calculate the ratio between
the size of the blur kernel and the disparities as
d
c
=
b
1
b
2
b
2
− b
1
(
1
a
2
−
1
a
1
)
l
D
. (4)
However, we can replace the terms in parentheses as
follows
1
a
2
−
1
a
1
=
1
b
1
−
1
b
2
=
b
2
− b
1
b
1
b
2
(5)
to obtain the final equation,
d
c
=
b
1
b
2
b
2
− b
1
b
2
− b
1
b
1
b
2
l
D
=
l
D
(6)
CODED APERTURE STEREO - For Extension of Depth of Field and Refocusing
107

(a) Captured image with circular aperture. (b) Captured image with coded aperture.
(c) Deblurred image with circular aperture. (d) Deblurred image with coded aperture.
Figure 9: Experiment 2: Deblurring of scene with depth variation.
where the ratio between the diameter of the blur circle
is directly proportional to the relative disparity from
the focus distance, and the constant of proportion is
the ratio between the diameter of the lens and the
length of the baseline.
More intuitively, as shown in the right image I
R
in Figure 4, the circle of confusion simultaneously
scales and shifts along with the distance, and the enve-
lope of the circle of confusion forms two lines cross-
ing at the focal point.
This conclusion makes it very simple to convert
the disparity between two images to the size of the
blur kernel. If the two optical parameters, the size
of the aperture, and the baseline length are precisely
known, we can directly convert the disparity to the
blur size. If not, we can simply use two point light
sources at different distances in the scene, and we
can measure the size of the blur kernel and dispar-
(a) Close-up of green
region in Figure 9(c).
(b) Close-up of green
region in Figure 9(d).
(c) Close-up of red re-
gion in Figure 9(c).
(d) Close-up of red re-
gion in Figure 9(d).
Figure 10: Close-ups of deblurred images (Figures 9(c) and
9(d)).
ity from the captured images to obtain the coefficient.
If a more precise estimate is needed, we can use the
simple least squares method.
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
108

Figure 5 illustrates an example of the relation-
ship between disparity and blur size. With point light
sources placed at varying distances, we measure the
size of the blur kernel and disparity. In the figure,
green crosses indicate measured points, while the red
line is a fitting line calculated using the least squares
method. Since the focus distance of the lens was set to
infinity, the size of the blur kernel size was estimated
to be zero when the disparity was also zero.
3.3 Extension of Depth of Field
With captured image y and known blur kernel f , a
latent, blur-free image x can be estimated by Wiener
deconvolution. Using a Fourier transform, we can cal-
culate Y (ω) as the frequency domain representation
of y and F (ω) as the frequency domain representa-
tion of f . Then, the Fourier transform of latent image
x can be calculated by
X (ω) =
F
∗
(ω)Y (ω)
|
F (ω)
|
2
+ σ
(7)
where F
∗
(ω) is the complex conjugate of F (ω) and σ
is a constant to avoid emphasis of noise where the blur
kernel has low power components or division by zero.
This term should be determined by the noise level of
the input images, and also used to select the appropri-
ate Zhou code (Zhou and Nayar, 2009). The original
scene x can be calculated by an inverse Fourier trans-
form of X (ω).
Since Wiener deconvolution is a processing in the
frequency domain, blur kernel f should be uniform
within the processed image. However, as the depth
of the scene is not uniform, the captured image must
be clipped out from the captured image using a win-
dow function, and the Wiener deconvolution applied
to each region. In the experiment, we used a Ham-
ming window as the window function, and the image
was clipped to 64 pixels square, shifting 8 pixels.
4 EXPERIMENTS
In this section, the results of three experiments are
given. First, robustness of stereo matching by Zhou’s
code is investigated by evaluating the matching er-
ror with images to which white noise has been in-
tentionally added. Second, an image of the depth of
field extension is shown by removing blur from the
captured image using the process shown in Figure 1.
And finally, we present the refocusing result, com-
puted from an all-in-focus image and depth map, to
be artificially focused on a distance different from the
captured image, and otherwise blurred.
The camera and lens used in the experiments were
a Nikon D200 and SIGMA EX 30mm f/1.4 EX DC,
respectively. The image format was 8 bit JPEG. In-
stead of using two cameras, a camera was placed on
a sliding stage, and images were captured by mov-
ing the camera laterally. The distance of the transla-
tion (length of the baseline) in the experiments was 14
mm. The aperture code used in the experiments was
one of Zhou’s codes for noise, σ = 0.005, in Figure
2, inserted at the rear of the lens. To avoid vignetting,
the f-number of the original lens aperture was set to
f/1.4. For comparison with normal aperture shapes,
the code mask was removed from the lens, and the f-
number of the original lens was set to f/5.0 to keep the
exposure value and shutter speed equal. As a result,
the area of the coded aperture was equal to that of the
circular aperture.
4.1 Experiment 1: Robustness of Stereo
Matching
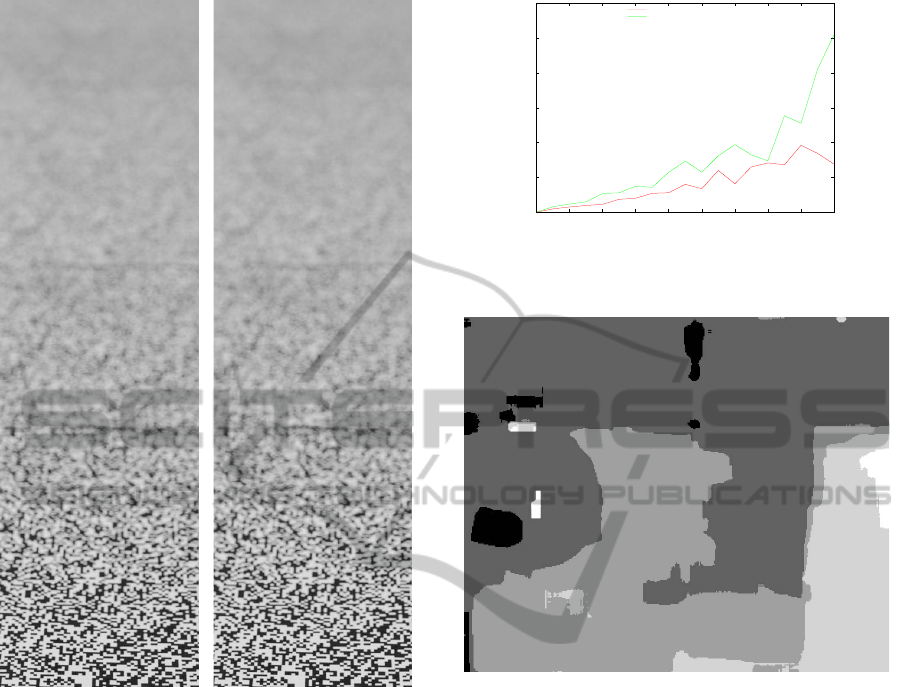
We conducted an experiment to evaluate the robust-
ness of the stereo matching with Zhoufs code. While
we used actual captured images, we intentionally
added white noise to the images.
A random black-and-white pattern with a 1-mm
grid size was printed on a sheet of paper and placed
on a table. Cameras were placed at oblique angles,
with the distance from the camera to the object vary-
ing along the vertical axis of the image. The depth
range was around 50 cm to 100 cm from the bottom
to the top of the image, and the focus distance was ad-
justed at the nearest distance of the object. Captured
images with circular and coded apertures are shown
in Figures 6(a) and 6(b), respectively.
From these images, we can see that the exposure
values of the normal and coded apertures are almost
the same, but compared with the image by the circular
aperture, the image with the coded aperture preserves
some texture information well, even in the heavily de-
focused regions.
To evaluate robustness of stereo matching, zero-
mean white noise was added to both captured images.
The variance of the noise ranged from 0 to 9.0 with
a 0.5 step, and the error ratio of stereo matching was
calculated.
Figure 7 shows the error ratio of stereo match-
ing, where the error ratio is defined as the number of
pixels whose disparity differs from that in the noise-
less image. The average error ratio is 3.22% and
1.72% for the circular and coded apertures, respec-
tively. As the variance increases, so too does the er-
ror ratio. However, the error ratio of the coded aper-
ture is always lower than that of the circular aperture.
CODED APERTURE STEREO - For Extension of Depth of Field and Refocusing
109

(a) Captured image. (b) All-in-focus image
(c) Refocused image.
Figure 11: Experiment 3: Refocusing.
This shows that broadband code such as Zhou’s code
makes stereo matching robust.
4.2 Experiment 2: Robustness of
Deblurring
We conducted a depth of field extension experiment
using a real scene.
For the scene shown in Figure 9, images were cap-
tured with circular and coded apertures, and we con-
ducted stereo matching and deblurring using our sys-
tem. In this experiment, the focus distance of the lens
was set to a point further than the furthest distance in
the scene to show the deblurring effect clearly. The
disparity map using the coded aperture is shown in
Figure 8.
Figures 9(a) and 9(b) show one of the captured im-
ages with circular and coded apertures, respectively,
while Figures 9(c) and 9(d) give the corresponding
results after deblurring. Figure 10 shows close-ups
of the rectangles in Figures 9(c) and 9(d). It is clear
that sharpness is greatly improved in images with the
coded aperture, while the result with the circular aper-
ture has slightly improved sharpness and does not
show much effect of deblurring.
4.3 Experiment 3: Refocusing
As an application of our method, we show an example
of a refocused image computed from an all-in-focus
image and a disparity map. The same setup as in ex-
periment 2 was used, with the focus set to the furthest
part in the scene to clearly show the effect of refo-
cusing. For the input image shown in Figure 11(a),
we can see the effect of blurring on a book placed
on the right side. In Figure 11(b), an all-in-focus im-
age is shown. Optical blur of the objects on the table
and the PRML book has been removed and the im-
age sharpened. The refocused image created by blur-
ring the all-in-focus image with the circular aperture
kernel and disparity map is shown in Figure 11(c).
Contrary to the input image, close objects are seen
sharply, while other distant objects are blurred in the
refocused image.
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
110

5 CONCLUSIONS
In this paper, we presented a depth of field extension
method for defocused images, which removes blur in
the captured image using coded aperture stereo and
Wiener deconvolution. We proved that disparity of
stereo matching is proportional to the size of the blur
kernel, and this theory makes PSF estimation from
disparity easy. We also showed that stereo matching
with a coded aperture makes stereo matching robust.
We showed through experiments that our system can
remove defocus blur from captured images accurately
by estimating the PSF from disparity and deblurring.
As an application, we presented a refocused image
computed from an all-in-focus image and a disparity
map.
In the experiments, instead of using a stereo cam-
era, we set a camera on a sliding stage and captured
the static scene. Nevertheless, using two cameras, it
is possible to use our method to capture a dynamic
scene.
In this paper, the same aperture pattern and focus
distance were used in the cameras. Our future work
aims to integrate Depth from Defocus and stereo, and
extend the theory to the case with different apertures
and focal settings.
ACKNOWLEDGEMENTS
This work was partially supported by Grant-in-Aid
for Scientific Research (B:21300067) and Grant-
in-Aid for Scientific Research on Innovative Areas
(22135003).
REFERENCES
Green, P., Sun, W., Matusik, W., and Durand, F. (2007).
Multi-aperture photography. In ACM SIGGRAPH
2007 papers, SIGGRAPH ’07, New York, NY, USA.
ACM.
Hiura, S. and Matsuyama, T. (1998). Depth measurement
by the multi-focus camera. In Computer Vision and
Pattern Recognition, 1998. Proceedings. 1998 IEEE
Computer Society Conference on, pages 953 –959.
Lam, E. Y. and Goodman, J. W. (2000). Iterative statistical
approach to blind image deconvolution. J. Opt. Soc.
Am. A, 17(7):1177–1184.
Levin, A. (2010). Analyzing depth from coded aperture
sets. In Proceedings of the 11th European conference
on Computer vision: Part I, ECCV’10, pages 214–
227, Berlin, Heidelberg. Springer-Verlag.
Levin, A., Fergus, R., Durand, F., and Freeman, W. T.
(2007). Image and depth from a conventional cam-
era with a coded aperture. In ACM SIGGRAPH 2007
papers, SIGGRAPH ’07, New York, NY, USA. ACM.
Liang, C.-K., Lin, T.-H., Wong, B.-Y., Liu, C., and Chen,
H. H. (2008). Programmable aperture photography:
multiplexed light field acquisition. In ACM SIG-
GRAPH 2008 papers, SIGGRAPH ’08, pages 55:1–
55:10, New York, NY, USA. ACM.
Nayar, S., Watanabe, M., and Noguchi, M. (1995). Real-
time focus range sensor. In Computer Vision,
1995. Proceedings., Fifth International Conference
on, pages 995 –1001.
Richardson, W. H. (1972). Bayesian-based iterative method
of image restoration. J. Opt. Soc. Am., 62(1):55–59.
Schechner, Y. Y. and Kiryati, N. (2000). Depth from defo-
cus vs. stereo: How different really are they? Int. J.
Comput. Vision, 39:141–162.
Veeraraghavan, A., Raskar, R., Agrawal, A., Mohan, A.,
and Tumblin, J. (2007). Dappled photography: mask
enhanced cameras for heterodyned light fields and
coded aperture refocusing. ACM Trans. Graph., 26.
Zhou, C., Lin, S., and Nayar, S. (2009). Coded aperture
pairs for depth from defocus. In Computer Vision,
2009 IEEE 12th International Conference on, pages
325 –332.
Zhou, C. and Nayar, S. (2009). What are good apertures
for defocus deblurring? In Computational Photogra-
phy (ICCP), 2009 IEEE International Conference on,
pages 1 –8.
CODED APERTURE STEREO - For Extension of Depth of Field and Refocusing
111
