BAYESIAN PERSPECTIVE-PLANE (BPP) FOR LOCALIZATION

Zhaozheng Hu

1, 2

and Takashi Matsuyama

Graduate School of Informatics, Kyoto University, Sakyo-Ku, Kyoto, Japan

College of Information Science and Technology, Dalian Maritime University, Dalian, China

Keywords: Vision-based Localization, Bayesian Perspective-plane (BPP), Plane Normal, Maximum Likelihood.

Abstract: The "perspective-plane" problem proposed in this paper is similar to the "perspective-n-point (PnP)" or

"perspective-n-line (PnL)" problems, yet with broader applications and potentials, since planar scenes are

more widely available than control points or lines in practice. We address this problem in the Bayesian

framework and propose the "Bayesian perspective-plane (BPP)" algorithm, which can deal with more

generalized constraints rather than type-specific ones to determine the plane for localization. Computation

of the plane normal is formulated as a maximum likelihood problem, and is solved by using the Maximum

Likelihood Searching Model (MLS-M). Two searching modes of 2D and 1D are presented. With the

computed normal, the plane distance and the position of the object or camera can be computed readily. The

BPP algorithm has been tested with real image data by using different types of scene constraints. The 2D

and 1D searching modes were illustrated for plane normal computation. The results demonstrate that the

algorithm is accurate and generalized for object localization.

1 INTRODUCTION

Vision-based localization has many applications in

computer vision, robotics, augmented reality (AR),

simultaneous localization and mapping (SLAM),

and photogrammetric communities (Hartley &

Zisserman, 2004; Desouza et al., 2002; Durrant-

Whyte & Bailey, 2006; Cham et al., 2010). The

basic objective is to compute the position of the

object or the camera in a reference coordinate

system by using either multiple (two or more) or

single image(s). For example, stereo vision is a

commonly used approach for localization from two

images, which can retrieve the 3D coordinates or

position of an object in the scene from image

disparity, baseline width, and camera focal length

(Hartley & Zisserman, 2004). Localization from

single view usually relies on "prior knowledge" of

the scene. In the literatures, many localization

algorithms were developed by utilizing specific

scene constraints, such as well-defined landmarks,

natural or artificial objects, and the abstract points or

lines, etc. For example, landmarks are commonly

used for localization (Adan, 2010). Face position can

be computed by referring to a 3D face model (Sun et

al., 2008). Single image of a window in the street is

possible to localize the camera (Johansson &

Cipolla, 2002). Camera pose can also be computed

from corner structure (Shi et al., 2004). Besides

these particular objects, many researches investigate

the localization problem from a set of abstract points

or lines, namely known as the perspective-n-point

(PnP) and perspective-n-line (PnL) problems (Wolfe

et al., 1991; Kneip et al., 2011; Hu & Matsuyama,

2011). Besides points and lines, the position can also

be computed from a plane or planar object. Planar

structure, i.e., the plane normal and distance, can be

computed from parallel lines, homography, conics,

control points, textures, etc. For example, Hu et al

determine the support plane from the geometric

constraints of three control points (Hu &

Matsuyama, 2011). With four or more planar points,

we can compute the homography and determine the

plane position by decomposition (Zhang, 2000). The

plane normal is also computed from vanishing line,

if two sets of parallel lines are available in the scene

(Lee et al., 2009). Other methods to compute the

plane by using conics, reference lengths, textures,

etc., are also reported in (Hartley & Zisserman,

2004; Guo & Chellappa, 2010; Witkin, 1981).

Existing methods for localization and planar

structure computation from single view are mostly

based on specific scene constraints. These methods

are not generalized or practical enough. On the one

hand, some strict constraints, which are required by

the type-specific algorithm, are not available in the

241

Hu Z. and Matsuyama T..

BAYESIAN PERSPECTIVE-PLANE (BPP) FOR LOCALIZATION.

DOI: 10.5220/0003818902410246

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 241-246

ISBN: 978-989-8565-04-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

scene. On the other hand, some constraints, which

are present in the scene, are difficulty to be utilized

by the type-specific algorithm. In this paper, we

propose the "perspective-plane" problem and

address it by the Bayesian perspective-plane (BPP)

algorithm. The proposed algorithm can utilize more

generalized planar and out-of-plane constraints to

determine the plane for localization.

2 FORMULATION OF

GEOMETRIC CONSTRAINTS

From projective geometry, a physical plane and its

image are related by a 3×3 homography matrix H as

follows (Hartley & Zisserman, 2004; Zhang, 2000)

xHX

1−

≅

(1)

where

≅

means equal up to a scale, x and X are the

coordinates for the image and physical point,

respectively. The homography is computed from the

plane normal and distance according to stratified

reconstruction theories (Hartley & Zisserman, 2004).

With the recovered 2D coordinates, more planar

geometric attributes, such as coordinate, distance,

angle, length ratio, curvature, shape area, etc., are

calculated readily. A metric reconstruction of the

plane is also feasible with known plane normal and

unknown distance. However, the absolute geometric

attributes, such as coordinates, distance, etc., are

equal to the actual ones up to a common scale. And

non-absolute geometric attributes, such as length

ratio, angle, etc., are equal to the actual ones.

Some out-of-plane geometric attributes can also

be computed with a reference plane. For example, an

orthogonal plane can be measured by referring to a

known plane (Wang et al., 2005). If the vanishing

line of a reference plane and one vanishing point

along a reference direction are known, object height,

distance, length ratio, angle, and shape area on the

parallel planes etc., are readily computed (Criminisi

et al., 2000). From projective geometry, both the

vanishing line and the vanishing point along the

normal are computed from the plane normal and the

calibration matrix. Also, if the plane distance is

unknown, those absolute out-of-plane geometric

attributes are computed up to a common scale, while

the non-absolute ones are equal to the actual ones.

Hence, we use

()

to denote the i

geometric

attribute, computed from the plane normal N. Scene

prior knowledge can be formulated into constraints

on plane normal. Let

be the deterministic value

of the geometric attribute that we know a prior. The

measurement error is defined as

(

)

(

)

iii

uNQNd

−

(2)

By forcing zero measurement error, we can derive

one geometric constraint on the plane normal

(

)

(

)

0: =−

iiii

uNQNdC

(3)

Eq. (3) holds for both planar and out-of-plane

constraints. Planar constraints are derived from prior

knowledge of planar features, while the out-of-plane

constraints are from the out-of-plane ones. The

planar features are those that lie on the plane, such

as the point, line, angle, curve, shape, etc., while the

other are defined as out-of-plane features, such as an

orthogonal line, an angle on another plane, etc. In a

similar way, we can derive a set of geometric

constraints as follow

(

)

(

)

{

}( )

MiuNQNdCC

iiii

,,2,10| "=

−

(4)

3 BAYESIAN

PERSPECTIVE-PLANE (BPP)

3.1 Localization from a Known Plane

An arbitrary planar point can be localized from a

known plane as follows

⎪

⎩

⎪

⎨

⎧

−

dXN

xKX

(5)

The first equation in Eq. (5) defines the back-

projection ray, where the 3D point X lies (Hartley &

Zisserman, 2004). It can be determined from the

camera calibration matrix and the image point. The

second one is the plane equation with the normal N

and distance d. If we use the plane to expand a

reference coordinate system, the camera can be

localized as well (Zhang, 2000).

3.2 Plane Normal from MLS-M

3.2.1 Maximum Likelihood Formulation

The plane normal is assumed uniform distribution if

there are no geometric constraint. The distribution

changes from uniform to non-uniform, given one

constrain. Distribution from a set of constraints is

expected to have a dominant peak, from which the

plane normal is solved. Therefore, computation of

the plane normal N is formulated as to maximize the

following conditional probability

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

242

()

CCCNP ,,,|maxarg

(6)

By using Bayes’ rule, Eq. (6) is transformed as

()

()()

()

CCCP

NPNCCCP

CCCNP

,,,

|,,,

,,,|

" =

(7)

Assume that all the constraints are conditionally

independent to each other so that we can derive

()()

∏

NCPNCCCP

||,,, "

(8)

Assume uniform distribution of plane normal and

we can substitute Eq. (8) into Eq. (7) to derive

()()

∏

∝

NCPCCCNP

|,,,| "

(9)

In order to solve Eq. (6), we need to model

()

NCP

, which is defined as the likelihood that the

constraint is satisfied, given the plane normal N.

We set the following rules to develop the model: 1)

the likelihood is determined by the measurement

error. More absolute measurement error yields lower

likelihood. The maximum likelihood is reached if

the measurement error is zero; 2) the maximum

likelihoods (for zero measurement errors) for

different constraints should be equal so that all

constraints contribute equally; 3) the measurement

error should be normalized to deal with the

geometric attributes in different forms, units, and

scales, etc. To meet these requirements, the

normalized Gaussian function was proposed to

model the likelihood as follows

()()

(

)

⎟

⎠

⎞

⎜

⎝

⎛

−=

exp

iii

uNdG

σπ

(10)

The measurement error is normalized by

from

Eq. (3). Obviously, Eq. (10) satisfies the first rule.

The likelihood also decreases with the absolute

measurement errors. The maximum likelihood is

reached at zero measurement error. In order to

satisfy the second rule, the standard deviations for

all Gaussian models should be equal:

Hence, the likelihood model is derived as

() ()()

()

⎟

⎠

⎞

⎜

⎝

⎛

−==

exp

σπ

NdGNCP

(11)

Substitution Eq. (11) into Eq. (9) yields

()

(

)

∏

⎟

⎠

⎞

⎜

⎝

⎛

−∝

CCCNP

exp,,,|

(12)

The plane normal is thus computed as

(

)

⎟

⎠

⎞

⎜

⎝

⎛

−

∑

expmaxarg

(13)

3.2.2 Searching for Maximum Likelihood

A maximum likelihood searching model (MLS-M)

is used to solve Eq. (13). Two searching modes of

2D and 1D are proposed in the following.

a. 2D searching mode

A unit normal corresponds to a point on the

Gaussian sphere surface so that the searching space

is defined. In practice, we search on the Gaussian

hemisphere to reduce the searching space into half,

because only the planes in front of the camera are

visible in the image. A uniform sampling is realized

by evenly partition Gaussian hemisphere, which can

be solved by using the recursive zonal equal area

sphere partitioning algorithm (Leopardi, 2004). The

likelihood for each sample is computed so that the

maximum likelihood is calculated by sorting, the

corresponding plane normal is then determined.

Since Gaussian sphere in 3D space is 2D, we call it a

2D searching mode.

b. 1D searching mode

1D searching mode is feasible if one linear

constraint is available in the scene. In practice, some

linear constraints can be derived from parallel lines,

orthogonal lines or planes, etc. We introduced the

1D searching mode by using orthogonal line as an

example. Let

be the orthogonal line, with the

image

. Because

is parallel to the plane normal,

the vanishing point

along the normal lies on

and satisfy the following equation

()

(

)

0=== NlKKNlVl

(14)

The normal N also lies on Gaussian sphere so that

(

)

⎪

⎩

⎪

⎨

⎧

NlK

(15)

Eq. (15) defines a circle in 3D space, which is the

intersection of the plane with the Gaussian sphere.

Therefore, we need to search on the circle (actually

half of the circle). Similarly, a uniform sampling on

the circle is required. The likelihood for each sample

is computed. And the maximum likelihood is finally

searched to solve the plane normal.

3.3 Plane Distance Computation and

Localization

Assume unit plane distance and re-write Eq. (5) as

BAYESIAN PERSPECTIVE-PLANE (BPP) FOR LOCALIZATION

243

⎪

⎩

⎪

⎨

⎧

′

−

xKX

(16)

Compared to Eq. (5), it can be derived that

≅

′

Hence, we can localize all the planar points in the

camera coordinate system up to a common scale. In

order to compute the actual coordinates, a reference

length or distance is required. For example, the scale

can be determined from the actual length

between two points A and B as follows

′

−

′

(17)

where

′

and

′

are the 3D coordinates of two

points that are computed from Eq. (16). With the

computed scale factor, the actual plane distance is

. And the actual 3D position is

′

(18)

4 EXPERIMENTAL RESULTS

The proposed algorithm was tested with two real

image experiments. A Nikon D700 camera was used

to generate the real images of 2218

×1416 (pixel)

resolution. It was calibrated with Zhang's calibration

algorithm (Zhang, 2000) with 1369.2-pixel focal

length and principle point at [1079, 720]

(pixel).

The calibration results were used for planar structure

computation and localization. As there are various

scene constraints in practice, it is difficult to discuss

all of them. We chose two representative constraint

types of known angle and length ratios to validate

the proposed model in the experiments.

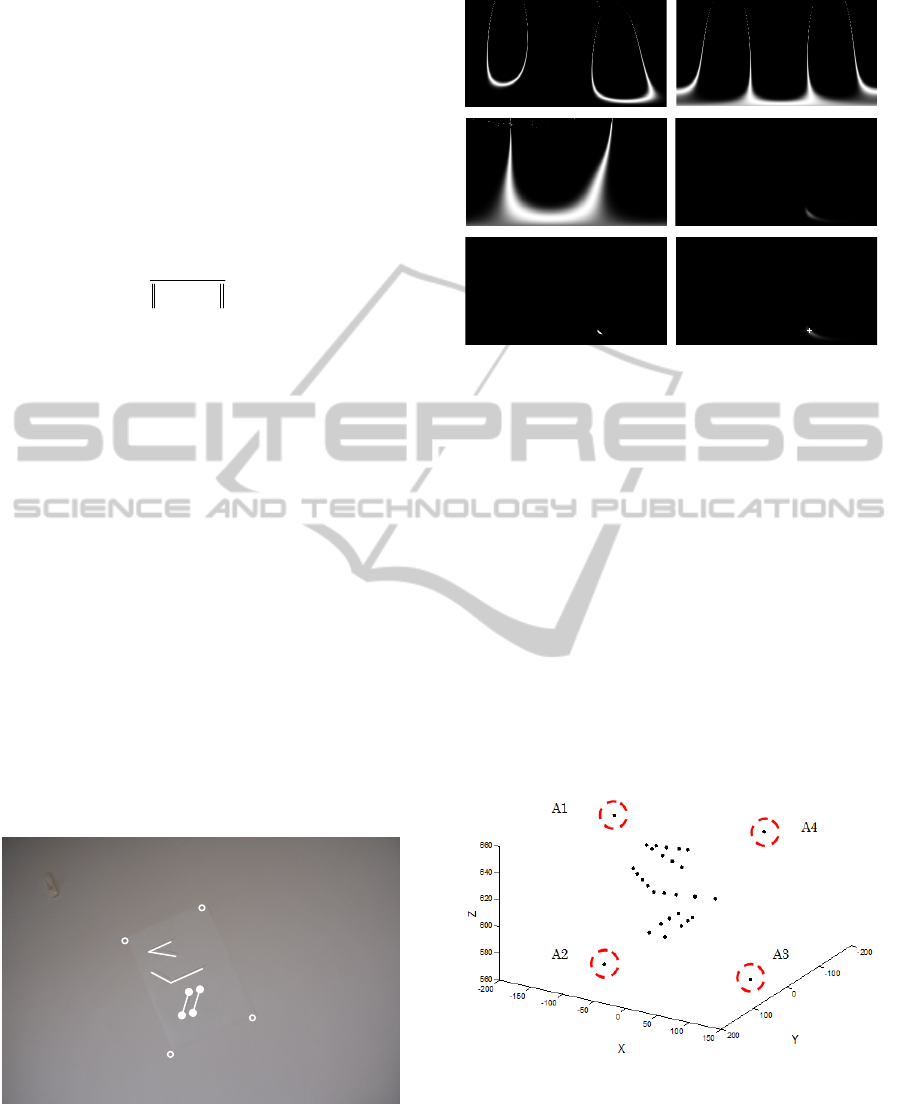
Figure 1: Three planar constrains (two known angles and

one length ratio) from lines and points for localization.

The algorithm was tested with planar constraints

first. Figure 1 shows an image of a white paper

attached on the wall. Six line segments were drawn

Figure 2: From upper left to lower right: (a) (b) (c)

likelihoods from three geometric constraints, (d) the joint

likelihood, (e) positions of the 30 normal of the highest

likelihoods; (f) the computed normal marked by ‘+’.

on the paper. We derived two angles (34.1 and 126.6

degrees) from L1-L2 and L3-L4, and one length

ratio between the distances of M1-M2 and M3-M4

to derive three planar constraints. The 2D searching

mode was applied then. The likelihoods from

different geometric constraints are shown in Figure

2(a)~(c), where the non-uniform distributions of the

plane normal are observed. The joint likelihood is

shown in Figure 2(d), where a bright area on the

bottom is observed. Figure 2(e) shows the 30 plane

normal with the highest likelihoods. The plane

normal computed from the joint likelihood map is

marked by '+' (see Figure 2(f)), with the result

[0.0993 0.1679 0.9808]

Figure 3: Localize points and lines in the camera

coordinate system (unit in mm).

The plane distance was computed by using the

reference length of the white paper (297mm). The

points on the plane were localized. Figure 3 shows

3D positions of the points on the six line segments,

and the four corners (A1~A4 marked by 'o'), all in

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

244

the camera coordinate system. The computation

results were validated as follow. The lengths of A2-

A3, A3-A4, and A1-A4 were computed from the

recovered 3D coordinates as 206.7, 294.6, and 211.8

(mm), respectively. Compared to ground truth data

(the size of the white paper), the absolute errors are

3.3, 2.4, and 1.8 (mm), corresponding to 1.6%,

0.8%, and 0.9% relative errors. It demonstrates that

the proposed model is accurate.

Figure 4: Localization from 3D corner constraints.

The algorithm was further tested with both planar

and out-of-plane constraints by using 1D searching

mode. As shown in Figure 4, a 3D corner structure

of a book is defined by the three orthogonal lines of

L1, L2, and L3. From these three lines, three planes

are defined as L1-L2, L1-L3, L2-L3. For each plane,

we derived two constraints: 1) one orthogonal line to

the plane; 2) one right angle between the other two

lines on the plane, as shown in Figure 4. They were

used to localize each plane.

Figure 5: From left to right: likelihoods of the normal of

the planes defined by: a) L1-L2, b) L1-L3, c) L2-L3.

The 1D searching mode was applied. The

searching circles were defined from the orthogonal

line constraints, on which 10,000 points were

uniformly sampled, respectively. The likelihoods for

each normal of the three planes were computed

afterwards (see Figure 5(a)~(c)). For each plane, two

peaks are observed from the likelihood curve, which

indicates two solutions (also see multiple solutions

in (Shi et al., 2004)). Hence, eight combinations for

the normal of the three planes are derived, two of

which satisfy the mutually orthogonality constraints.

In order to eliminate the ambiguity, we utilized one

more constraint from the ratio of the length (M0-

M1) to the width (M0-M2) to uniquely determine

the normal of the plane L1-L2. The likelihood from

such constraint and the joint likelihood are

illustrated in Figure 6. In the joint likelihood, a

unique peak is observed (see Figure 6(b)). From the

joint likelihood, the maximum likelihood was

searched and the normal to the L1-L2 plane was

computed as [-0.0022 0.8425 0.5387]

. With the

computed L1-L2 normal, the normal for the other

two planes were also uniquely determined.

Figure 6: From left to right: a) likelihood from the length

ratio constraint; b) joint likelihood from all constraints.

We used one actual length to compute the plane

distance and localize the corner points in the camera

coordinate system. Their 3D positions are shown in

Figure 7. The camera was also localized in the

reference coordinate system, defined by the corner

structure, with M0 as the origin, and L1, L2, L3 as

the three axes, where the camera position is [-21.64,

-23.82, -12.26]

(in cm). Hence, the object and the

camera were localized from each other. We

validated the results as follows. The calculated 3D

coordinates were used to fit the three lines. The lines

are mutually orthogonal and have an angle of 90

degrees in between, which are used as ground truth.

The computed angles in-between are 89.4, 88.1, and

94.1 degrees, respectively, with the absolute errors

of 0.6, 1.9, and 4.1 degrees. The relative errors are

0.7%, 2.1%, and 4.6%, with the average 2.4%. The

results demonstrate that the algorithm is accurate.

Figure 7: Localize the four corner points in the camera

coordinate system (unit in cm)

5 CONCLUSIONS

In this paper, we proposed the Bayesian perspective-

0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Number of sampled normal

The relative probability

0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Number of sampled normal

The relative probability

0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Number of sampled normal

The relative probability

0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Number of sampled normal

The relative probability

0 1000 2000 3000 4000 50 00 6000 700 0 8000 9000 10 000

0.5

1.5

2.5

x 10

-6

Number of sampled normal

The relative probability

-25

-20

-15

-10

-5

-4

-2

BAYESIAN PERSPECTIVE-PLANE (BPP) FOR LOCALIZATION

245

plane (BPP) algorithm to address the "perspective-

plane" problem, which can localize object/camera by

determining planar structure from more generalized

planar and out-of-plane constraints. Computation of

the plane normal is formulated as a maximum

likelihood problem and is solved by MLS-M. Both

2D and 1D searching modes were presented. The

BPP algorithm has been tested with real image data.

The results show that the proposed algorithm is

generalized to utilize different types of constraints

for accurate localization.

ACKNOWLEDGEMENTS

The work presented in this paper was sponsored by a

research grant from the Grant-In-Aid Scientific

Research Project (No. P10049) of the Japan Society

for the Promotion of Science (JSPS), Japan, and a

research grant (No. L2010060) from the Department

of Education (DOE), Liaoning Province, China.

REFERENCES

Hartley, R., and Zisserman, A., 2004. Multiple view

geometry in computer vision, Cambridge, Cambridge

University Press, 2

Edition.

Desouza, G. N., and Kak, A. C., 2002. Vision for mobile

robot navigation: a survey, IEEE Trans on Pattern

Analysis and Machine Intelligence, 24(2): 237-267.

Durrant-Whyte, H. and Bailey, T., 2006. Simultaneous

Localization and Mapping (SLAM): part I the

essential algorithms, IEEE Robotics and Automation

Magazine, 13 (2): 99-110.

Cham, T., Arridhana, C., Tan, W. C., Pham, M. T., Chia,

L. T., 2010. Estimating camera pose from a single

urban ground-view omni-directional image and a 2D

building outline map, IEEE International Conference

on Computer Vision and Pattern Recognition (CVPR),

IEEE Press.

Adan, A., Martin, T., Valero, E., Merchan, P., 2009.

Landmark real-time recognition and positioning for

pedestrian navigation, CIARP, Guadalajara, Mexico,

Sun, Y., and Yin, L., 2008. Automatic pose estimation of

3D facial models, IEEE International Conference on

Pattern Recognition (ICPR), IEEE Press.

Johansson, B., and Cipolla, R., 2002. A system for

automatic pose-estimation from a single image in a

city scene, In IASTED Int. Conf. Signal Processing,

Pattern Recognition and Applications, Crete, Greece

Shi, F., Zhang, X., and Liu, Y., 2004. A new method of

camera pose estimation using 2D-3D corner

correspondence, Pattern Recognition Letters, 25(10):

805-809.

Wolfe, W., Mathis, D., Sklair, C., and Magee, M., 1991.

The perspective view of three Points, IEEE

Transaction on Pattern Analysis and Machine

Intelligence, 13(1): 66-73.

Kneip, L., Scaramuzza, D., and Siegwart, R., 2011. A

novel parameterization of the perspective-three-point

problem for a direct computation of absolute camera

position and orientation, IEEE International

Conference on Computer Vision and Pattern

Recognition (CVPR), IEEE Press.

Hu, Z., and Matsuyama, T., 2011. Perspective-three-point

(P3P) by determining the support plane, International

Conference on Computer Vision Theory and

Applications (VISAPP), SciTePress.

Zhang, Z., 2000. A flexible new technique for camera

calibration, IEEE Transactions on Pattern Analysis

and Machine Intelligence, 22(11):1330-1334.

Lee, D. C., Hebert, M., and Kanade, T., 2009. Geometric

reasoning for single image structure recovery, IEEE

International Conference on Computer Vision and

Pattern Recognition (CVPR), IEEE Press.

Guo, F., and Chellappa, R., 2010. Video metrology using a

single camera, IEEE Trans on Pattern Analysis and

Machine Intelligence, 32(7): 1329 -1335.

Witkin, A. P., 1981. Recovering surface shape and

orientation from texture, Artificial Intelligence,

17(1-3): 17-45.

Wang, G., Hu, Z., Wu, F., and Tsui, H., 2005. Single view

metrology from scene constraints,

Image and Vision

Computing, 23(9): 831-840.

Criminisi, A., Reid, I., and Zisserman, A., 2000. Single

view metrology, International Journal of Computer

Vision, 40(2): 123-148.

Leopardi, P., 2006. A partition of the unit sphere into

regions of equal area and small diameter, Electronic

Transactions on Numerical Analysis, 25(12):309-327.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

246