STEREO VISION-BASED 3D CAMERA POSE AND OBJECT

STRUCTURE ESTIMATION

An Application to Service Robotics

Sorin M. Grigorescu, Tiberiu T. Cocias¸, Gigel Maces¸anu and Florin Moldoveanu

Department of Automation, Transilvania University of Bras¸ov, Mihai Viteazu 5, 500174, Bras¸ov, Romania

Keywords:

Robot Vision, 3D Reconstruction, Stereo Vision, Volumetric Object Modeling.

Abstract:

In this paper, a robotic pose (position and orientation) estimation and volumetric object modeling system is

proposed. The main goal of the methods is to reliably detect the structure of objects of interest present in a

visualized robotic scene, together with a precise estimation of the robot’s pose with respect to the detected

objects. The robustness of the robotic pose estimation module is achieved by ﬁltering the 2D correspondence

matches in order to detect false positives. Once the pose of the robot is obtained, the volumetric structure of

the imaged objects of interest is reconstructed through 3D shape primitives and a 3D Region of Interest (ROI).

1 INTRODUCTION

In 3D robotic scene perception, there are usually two

types of vision sensors used for acquiring visual in-

formation, that is, stereo vision cameras and range

sensors such as laser scanners or 3D Time-of-Flight

(ToF) cameras (Hussmann and Liepert, 2007). In the

process of stereo vision based 3D perception and ego-

motion estimation, the stereo correspondence prob-

lem has to be solved, i.e. the corresponding feature

points, necessary for 3D reconstruction, have to be ex-

tracted from both stereo images (Brown et al., 2003).

In contrast, stereo vision range sensing devices pro-

vide direct capturing of 3D scenes, delivering a pure

stereo depth image in form of 3D point clouds. In

the case of range sensors, the obtained depth informa-

tion can have different error values, depending on the

sensed surface. This phenomenon makes stereo vi-

sion a more reliable solution for autonomous robotic

systems that operate in real world environments.

Camera pose estimation has been studied within

the Simultaneous Localization and Mapping (SLAM)

context. Using detected visual information, motion

estimation techniques can provide a very precise ego-

motion of the robot. The main operation involved in

stereo based robotic perception is the computation of

the so-called correspondence points used for calculat-

ing the 3D pose of the robot’s camera (Geiger et al.,

2011). The most common features used in this con-

text are points localized through corner detectors such

as Harris. Based on the extracted features, the robot’s

motion can be extracted with the help of estimators

such as the Kalman or Particle Filter.

In the last years, the 3D reconstruction and mod-

eling of objects has become a topic of interest for sev-

eral ﬁelds of research such as robotics, virtual real-

ity, medicine, surveillance and industry (Davies et al.,

2008). The main contributions of the presented paper

may be summarized as follows:

1. camera pose and 3D scene structure estimation

pipeline for on-line scene understanding;

2. automatic calculation of a 3D ROI for initializing

the 3D object volumetric estimation algorithm;

3. object grasping points calculation via 3D volu-

metric modeling from generic shape primitives in

highly noisy data (e.g. disparity images).

2 CAMERA POSE ESTIMATION

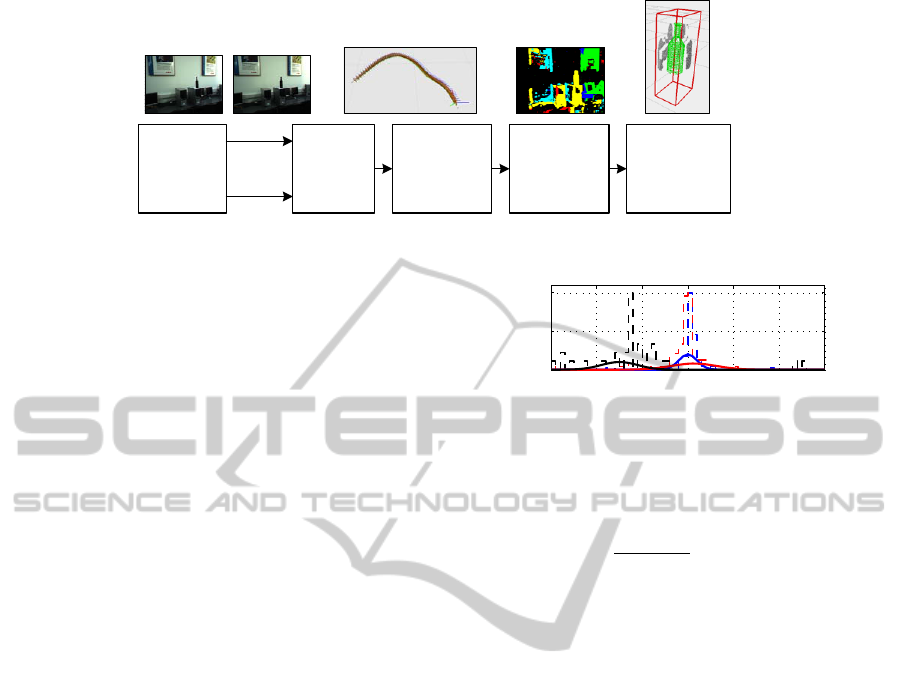
The block diagram of the proposed vision system is

presented in Fig. 1. The sequence of stereo images

is organized into so-called tracks which include key

features from the imaged scene and geometric con-

straints which are used to solve the pose estimation

problem. One of these elements are the matched 2D

feature points between the left and the right images of

the stereo camera. The accuracy of pose estimation is

directly dependent on the precision of 2D correspon-

dence matching. In order to ﬁlter out bad matches,

355

M. Grigorescu S., T. CociaÈ

Z T., MaceÈ

Zanu G. and Moldoveanu F..

STEREO VISION-BASED 3D CAMERA POSE AND OBJECT STRUCTURE ESTIMATION - An Application to Service Robotics.

DOI: 10.5220/0003819403550358

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 355-358

ISBN: 978-989-8565-04-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

Stereo

Image

Acquisition

Track

Geometry

Estimation

Probabilistic

Filtering and

Camera Pose

Estimation

Object

Segmentation

and

Classification

Right

Image

Left

Image

Volumetric

Modeling and

Object Fitting

Figure 1: Block diagram of the proposed camera pose estimation and object volumetric modeling architecture.

a probabilistic ﬁltering approach, which exploits the

geometrical constraints of the stereo camera, is pro-

posed.

2D feature points have been extracted via the

Harris corner detector, followed by a correspondence

matching using a traditional cross-correlation simi-

larity measure. Secondly, a matching is performed

between the 2D feature points in consecutive stereo

images, that is, between images acquired under ca-

mera poses C(k) and C(k + 1). As convention,

these matches are calculated for the left camera only.

Knowing the 3D positions of the 2D points matched

between adjacent images, the pose of the camera can

be calculated through a Perspective-N-Point (PNP) al-

gorithm (Hartley and Zisserman, 2004).

The obtained pose is further reﬁned using a

Kalman ﬁlter. Once the camera pose estimation prob-

lem has been solved, the 3D relation between the

robot and the imaged objects of interest has to be cal-

culated, that is, the establishment of the 3D positions

of the objects grasping points. This process is divided

into two stages. An initial raw object localization is

obtained through a depth image segmentation and ob-

ject classiﬁcation. Further, the detection of the 3D

grasping points is calculated by statistically ﬁtting a

shape primitive, based on the object classiﬁcation in-

formation. One of the main contributions of the pa-

per is actually the calculation of an object’s grasping

points through a shape primitive. As it will be ex-

plained, the primitive is independent of a particular

object shape, its ﬁtting being guided by so-called pri-

mitive control points. In other words, a shape can be

ﬁtted to a broad range of objects belonging to that spe-

ciﬁc class.

The process of matching stereo features is usu-

ally corrupted by noise and delivers false matches

along with the true correspondences. In order to over-

come this problem, we have chosen to ﬁlter out the

bad matches by exploiting the geometrical relations

within a stereo camera. Namely, we take into ac-

count that the majority of the points are true positive.

Hence, we can approximate the probability density of

−30 −20 −10 0 10 20 30

0.5

Degrees

Slope

Figure 2: Slope ﬁltering models.

the real matches by calculating the slope of the line

connecting the correspondences in two images:

m =

− p

, m ∈ M, (1)

where m is the slope between the left and right im-

age points p

(x, y) and p

(x, y), respectively. Taking

into account a Gaussian probability distribution of the

slope, a Maximum Likelihood Estimator (MLE) has

been used for calculating the parameters of the model,

that is the mean θ

and variance θ

θ = argmax

θ∈Θ

L(θ|M), (2)

where

θ is the obtained maximum likelihood estimate

for the Gaussian Probability Distribution Function

(PDF) p(M|θ

, θ

) describing the distribution of the

lines slope. In Fig. 2, three examples of slope PDF es-

timation can be seen. Using the obtained model, the

feature points can be classiﬁed into inliers and out-

liers, as in the classical RANSAC approach.

Once a certain camera pose has been calcu-

lated, it is ﬁltered out using a standard Kalman

ﬁlter with a state vector deﬁned as the mea-

sured rotation and translation of the sensor x =





. The transition matrix F

of the Kalman update equation x(k + 1) = F · x(k) +

w(k) encodes a constant camera velocity, with zero

acceleration. One major problem that has to be solved

in depth map fusion is the redundant information

coming from overlapping projected disparity images.

In order to save computation time, we have consid-

ered as valid voxels those ones visible in the newest

images acquired from the stereo camera. An example

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

356

Figure 3: Annotated 3D model from depth maps fusion.

of depth maps fusion within a robotic scene is given

in Fig. 3.

3 3D OBJECT VOLUMETRIC

MODELING

In order to ﬁt a shape primitive over the depth infor-

mation, the imaged objects have to be segmented and

classiﬁed. The feature vector used for this operation

is composed of the camera-object distance, described

by the disparity map, and the color distribution of the

objects represented in the HSV (Hue, Value, Satura-

tion) color space. The segmentation result classiﬁes

image pixels into object classes, as seen in Fig. 1.

The 2D segmentation information will be further used

for deﬁning a 3D ROI, which actually initializes the

shape ﬁtting algorithm. This is the starting point used

for deforming the shape primitive in order to ﬁt the

segmented object.

An object ROI is deﬁned in a stereo image pair

as the feature vector [p

, p

], i = 1, 2, 3, 4, contain-

ing the four corresponding 2D points in the left and

right images. Knowing the geometry of the stereo ca-

mera, the ROI vector can be reprojected into a vir-

tual 3D environment by calculating the disparity be-

tween p

and p

(Brown et al., 2003). The volu-

metric properties of the ROI, namely its 3D volume,

are calculated from the reprojected depth map, that

is, from the 3D distribution of the disparity points

calculated using the robust Block Matching approach

from (Grigorescu and Moldoveanu, 2011). The center

of the ROI over the Z axis is given by the highest dis-

parity points density obtained as a maximization over

the disparity value. The front and back positions of

the ROI are given by the nearest and farthest values in

the disparity. An example of a 3D ROI can be seen in

Fig. 4.

A shape primitive is represented as a Point Dis-

tribution Model (PDM) containing a vector of 3D lo-

cations S related to a common reference coordinate

system:

Figure 4: Reprojected 3D ROI and PDM mesh primitive.

(a) (b) (c)

Figure 5: Object shape primitive ﬁtting example. (a) Shape

primitive. (b) PDM model with control points marked with

red. (c) Deformed shape using a control point (affected

points marked with blue).

(i)

∈ S, i = 1, 2, ..., n

, (3)

where x is a point on the primitive shape and n

the

total number of primitive points. A mesh PDM exam-

ple can be seen in Fig. 5(a). The 3D ROI is used to

position the shape on the center of gravity of the ROI.

Once it is centered, its rotation, translation and scal-

ing is modiﬁed through a similarity transform:

new

= sR(X

old

+ T ), (4)

where X

old

and X

new

are the old and new 3D positions

of the primitive shape points, R and t are rotation and

translation matrices, respectively, and s represents a

scaling factor.

The last step in the proposed vision system is the

ﬁtting of the object’s primitive on the disparity infor-

mation. This procedure is performed using a set of so-

called control points which regulate the structure of

the shape. Such control points have been introduced

in medical imaging for modeling deformable shapes

such as the hearth (Zheng et al., 2008). To the best

of our knowledge, this is the ﬁrst application of con-

trol points ﬁtting a shape primitive in a stereo-vision

based system used in visual guided object grasping.

In the PDM from Fig. 5(b), the control points are re-

presented as the red locations. In the example from

Fig. 5(c), the shape is deformed by changing the lo-

cation of one control point. Following a simple linear

transformation, the neighboring points are automati-

STEREO VISION-BASED 3D CAMERA POSE AND OBJECT STRUCTURE ESTIMATION - An Application to

Service Robotics

357

cally translated with respect to the new position of the

control point.

In order to drive the control points to their opti-

mal 3D locations, a relation between the disparity in-

formation contained within the ROI and the control

points on the shape primitive had to be derived. This

is accomplished by estimating the surface normal of

the disparity areas with respect to the control points,

that is, each control points if moved in the direction of

the nearest disparity surface according to its normal.

The advantage of modeling the complete 3D shape

of the objects for grasping purposes plays a crucial

role in the grasping procedure. Namely, if each ob-

ject 3D point is precisely related to the pose of the

robotic system, obtained through the algorithm from

Section 2, then the control precision of autonomous

robots equipped with redundant manipulators is much

higher than for the case when object grasping points

are directly extracted from 2D visual information.

Table 1: Statistical position and orienation errors allong

the three Cartesian axes between the proposed and marker

based 3D camera pose estimation.

[m; deg] Y

[m; deg] Z

[m; deg]

Max err. 0.049; 4.2 0.059; 5.6 0.101; 10.1

Mean 0.013; 0.7 0.014; 0.7 0.042; 0.6

Std. dev. 0.021; 2.3 0.02; 2.6 0.064; 5.5

4 PERFORMANCE EVALUATION

The evaluation of the proposed machine vision system

has been performed with respect to the real 3D poses

of the objects of interest. The real 3D positions and

orientations of the objects of interest were manually

determined using the following setup. On the imaged

scene, a visual marker, considered to be the ground

truth information, was installed in such a way that the

poses of the objects could be easily measured with re-

spect to the marker. The 3D pose of the marker was

detected using the ARToolKit library which provides

subpixel accuracy estimation of the marker’s location

with an average error of ≈ 5mm. By calculating the

marker’s 3D pose, a ground truth reference value for

camera position and orientation estimation could be

obtained using the inverse of the marker’s pose ma-

trix. Further, the positions of the camera poses were

calculated using the proposed system. The results

were compared to the ground truth data provided by

the ARToolKit marker.

The marker-less pose estimation algorithm de-

scribed in this paper delivered a camera position and

orientation closely related to the ground truth va-

lues. This correlation can be easily observed when

analysing the statistical error results, given in Tab. 1,

between the two approaches. Namely, for both the

position and orientation, the errors are small enough

to ensure a good spatial localization of the camera, or

robot, and also to provide reliable depth maps fusion.

5 CONCLUSIONS

In this paper a camera pose and 3D object volumet-

ric system for service robotics purposes has been pro-

posed. Its goal is to precisely determine the 3D struc-

ture of the imaged objects of interest with respect to

the pose of the camera, that is, of the robot itself. As

future work, the authors consider the speed enhance-

ment of the proposed system using state of the art par-

allel processing equipment.

ACKNOWLEDGEMENTS

This paper is supported by the Sectoral Oper-

ational Program Human Resources Development

(SOP HRD), ﬁnanced from the European So-

cial Fund and by the Romanian Government un-

der the projects POSDRU/89/1.5/S/59323 and POS-

DRU/107/1.5/S/76945.

REFERENCES

Brown, M., Burschka, D., and Hager, G. (2003). Advances

in Computational Stereo. IEEE Trans. on Pattern

Recognition and Machine Intelligence, 25(8):993–

1008.

Davies, R., Twining, C., and Taylor, C. (2008). Statisti-

cal Models of Shape: Optimisation and Evaluation.

Springer.

Geiger, A., Ziegler, J., and Stiller, C. (2011). StereoScan:

Dense 3D Reconstruction in Real-time. In IEEE Intel-

ligent Vehicles Symposium, Baden-Baden, Germany.

Grigorescu, S. and Moldoveanu, F. (2011). Controlling

Depth Estimation for Robust Robotic Perception. In

Proc. of the 18th IFAC World Congress, Milano, Italy.

Hartley, R. and Zisserman, A. (2004). Multiple View Geom-

etry in Computer Vision. Cambridge University Press.

Hussmann, S. and Liepert, T. (2007). Robot Vision Sys-

tem based on a 3D-TOF Camera. In Instrumenta-

tion and Measurement Technology Conference-IMTC

2007, Warsaw, Poland.

Zheng, Y., Barbu, A., Georgescu, B., Scheuering, M., and

Comaniciu, D. (2008). Four-Chamber Heart Model-

ing and Automatic Segmentation for 3D Cardiac CT

Volumes Using Marginal Space Learning and Steer-

able Features. IEEE Trans. on Medical Imaging,

27(11):1668–1681.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

358