
SEGMENTATION OF PLANAR STRUCTURES IN BIOIMAGING
A. Martinez-Sanchez
1
, I. Garcia
2
and J. J. Fernandez
3
1
Grupo Supercomputacion y Algoritmos, Universidad de Almeria, Almeria, Spain
2
Grupo Supercomputacion y Algoritmos, Universidad de Malaga, Malaga, Spain
3
Centro Nacional de Biotecnologia (CSIC), Madrid, Spain
Keywords:
Planar Structures, Segmentation, Feature Detection, Biomedical Imaging.
Abstract:
This work presents an approach to detection of planar structures in three-dimensional (3D) datasets obtained
by different bioimaging modalities. The strategy has already turned out to be effective to segment membranes
from 3D volumes in the field of electron tomography, an emerging and powerful technique in structural and
cellular biology. This approach can also be useful to detect planar structures in general in other bioimaging
modalities. The goal of this position paper is to present this approach to the computer vision community and
illustrate the performance on a number of representative bioimaging datasets.
1 INTRODUCTION
The advent of biological imaging has made it possi-
ble to observe, directly or indirectly, the molecular
and cellular architecture and interactions that under-
lie essential functions within cells and tissues (Chan-
dler and Roberson, 2009). The availability of imaging
techniques (optical, confocal, electron microscopies,
electron tomography, just to name a few) in biology
laboratories is growing rapidly. So does the need
for image processing methods that facilitate analy-
sis and interpretation at different scales of resolution
and complexity. In this regard segmentation, which
intends to semantically decompose the datasets into
their structural components, plays a central role.
Structures that can be considered as planes at lo-
cal scale are often found in bioimaging datasets. Bi-
ological membranes are one of the best examples.
Membranes encompass compartments within biolog-
ical specimens, define the limits of the intracellular
organelles and the cells themselves, etc. Detection
of planar structures in general is important towards
(semi-)automated segmentation of the whole datasets.
Recently, we have presented an approach based on
local differential information that succeeds in seg-
menting biological membranes (or any planar struc-
ture in general) in three-dimensional (3D) datasets
obtained by electron tomography (ET) (Martinez-
Sanchez et al., 2011). ET nowadays proves to be one
of the leading techniques for visualizing the molecu-
lar organization of the cell environment (Frank, 2006;
Lucic et al., 2005). In this field, manual segmentation
still remains prevalent because no computational me-
thod has stood out as general applicable yet due to dif-
ferent reasons (they were case-specific, or limited per-
formance under low signal-to-noise ratio, difficult pa-
rameter tuning, user-intervention required, etc) (Volk-
mann, 2010). In manual segmentation, the user delin-
eates the features of interest using visualization tools,
which is tedious and subjective.
This position paper aims to present our approach
to detect planar structures to the computer vision
community and show its performance on datasets de-
rived from different bioimaging modalities, includ-
ing others than ET. Based on a Gaussian model for
the thickness of the planes, the procedure relies on
the characterization of structures at a local scale us-
ing differential information. Later, the integration at a
global scale yields the definite detection.
2 DETECTION OF PLANES
2.1 Model for the Planar Structure
In experimental datasets and at a local level, the pla-
nar structure has certain thickness and the density
along the direction normal to the plane progressively
decreases as a function of the distance to the centre of
the plane (Fig. 1) (Fernandez and Li, 2003; Fernandez
and Li, 2005). This density variation can be modelled
by a Gaussian function (Fig. 1):
I(r) =
D
0
√
2πσ
0
e
−
r
2
2σ
2
0
(1)
42
Martinez-Sanchez A., Garcia I. and J. Fernandez J..
SEGMENTATION OF PLANAR STRUCTURES IN BIOIMAGING.
DOI: 10.5220/0003819800420047
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 42-47
ISBN: 978-989-8565-04-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

where r runs along the normal to the plane, D
0
is a
constant to set the maximum density value (at the cen-
tre of the plane) and σ
0
is related to its thickness.
Figure 1: Plane model and the density profile across it.
The eigen-analysis of the density function at
point p = (x,y,z) of the plane yields the eigenvec-
tors
−→
v
1
,
−→
v
2
and
−→
v
3
with eigenvalues |λ
1
| >> |λ
2
| ≈
|λ
3
| (Fig. 1) (Fernandez and Li, 2003; Fernandez and
Li, 2005). This reflects that there are two directions
(
−→
v
2
,
−→
v
3
) with small density variation and the largest
variation runs along the direction perpendicular to the
plane (
−→
v
1
, parallel to r, i.e.
−→
v
1
||r ).
2.2 Scale-space
The scale-space theory was formulated in the
80s (Koenderink, 1984; Witkin, 1983) and allows
isolation of the information according to the spatial
scale. At a given scale σ, all the features with a size
smaller than the scale are filtered out whereas the oth-
ers are preserved. Therefore, the scale-space is useful
to focus on the structures of a particular size, ignoring
other smaller or spurious details. A scale-space for a
volume f can be generated by convolving f with a set
of kernels with size σ (Lindeberg, 1990). In this work
we have used a recursive implementation of the Gaus-
sian kernel with standard deviation σ, G(x;σ) (Young
and van Vliet, 1995).
To analyze the scale-space applied to the plane
model, it can be assumed without loss of generality
that r runs along the x direction (i.e.
−→
v
1
||r||x), hence
reducing the problem to one dimension (along x).
Given the Gaussian plane profile I (Eq. 1), ignoring
constants, and taking into account that the convolu-
tion of two continuous Gaussian functions yields an-
other Gaussian function whose variance is the sum of
the variances (Florack et al., 1992), the plane model
with thickness σ
0
at a scale σ is:
L(x;σ) = G(x;σ) ∗I(x) = G(x;
q
σ
2
+ σ
2
0
) (2)
2.3 Local Detector and Plane Strength
Now it is possible to define a detector for the plane
model at a given scale σ (Eq. (2)). This detector is
based on differential information, as it has to ana-
lyze local structure. In order to make it invariant to
the plane direction, the detector is established along
its normal (i.e. the direction of the maximum cur-
vature) at the local scale. An eigen-analysis of the
Hessian matrix is well suited to determine such di-
rection (Frangi et al., 1998). At every voxel of the
volume, the Hessian matrix is defined by:
H =
L
xx
L
xy
L
xz
L
xy
L
yy
L
yz
L
xz
L
yz
L
zz
(3)
where L
ij
=
∂
2
I
∂i∂j
∀i, j ∈ (x,y,z). The Hessian matrix
provides information about the second order local in-
tensity variation. The first eigenvector
−→
v
1
resulting
from the eigen-analysis is the one whose eigenvalue
λ
1
exhibits the largest absolute value and points to the
direction of the maximum curvature (second deriva-
tive).
The Hessian matrix of the plane model of the pre-
vious section (i.e. with maximum curvature along x)
at a scale σ has all directional derivatives null, except
L
xx
. As a result, λ
1
= L
xx
and
−→
v
1
= (1,0,0). Along
the direction normal to the plane, λ
1
turns out to be
negative where the plane has significant values and
its absolute value progressively decreases from the
centre towards the extremes of the plane, as shown
in Fig. 2(top). Therefore, we propose the use of |λ
1
|
as a local plane detector (also known as local gauge).
In practice, in experimental studies λ
2
and λ
3
are not
null. Thus, a more realistic gauge would be:
R =
|λ
1
|−
√
λ
2
λ
3
λ
1
< 0
0 λ
1
≥ 0
(4)
where
√
λ
2
λ
3
is the geometrical mean between λ
2
and
λ
3
.
Unfortunately, R is still sensitive to other local
structures that may produce false positives along the
maximum curvature direction. To make the gauge ro-
bust and more selective, it is necessary to define de-
tectors for these cases. First, the noisy background
SEGMENTATION OF PLANAR STRUCTURES IN BIOIMAGING
43

Figure 2: Second derivative L
xx
of the plane model (σ
0
= 1)
at a scale σ = 1 (top) and Gauges for the density profile of a
plane with σ
0
= 1 at a scale σ = 1 (blue): R
2
(red), S (cyan)
and plane strength P (green). The profile across the plane, S
and P are normalized in the range [0, 1]. R
2
keeps the scale
relative to S.
in the volume may generate false positives. However,
the background usually has a density level different
from that shown by the structures of interest. A strat-
egy based on a density threshold t
l
(Fernandez and Li,
2005) helps to get rid of these false positives.
Local structures resembling ‘density steps’ in the
volume also make the gauge R produce a false peak.
A suitable detector for a local step is the edge
saliency (Lindeberg, 1998):
S = L
2
x
+ L
2
y
+ L
2
z
(5)
where L
i
=
∂I
∂i
∀i ∈ (x,y,z). A plane exhibits a high
value of S at the extremes and a low value at the centre
(Fig. 2(bottom)). Based on their response to a plane,
the ratio between the squared second-order and first-
order derivatives (i.e. R
2
/S) quantifies how well the
local structure around a voxel fits the plane model and
not a step. We thus define plane strength as:
P =
(
R
2
S
,(L > t
l
) and
sign
∂R
∂r
6= sign
∂S
∂r
0 , otherwise
(6)
The first condition in Eq. (6) denotes the density
thresholding described above. The second condition
represents the requirement that the slopes of R and
S in the gradient direction must have opposite signs.
This condition is important to restrict the response of
that function for steps (see Fig. 2(bottom)) . If the
local structure approaches the plane model, P will
have high values around the centre of the plane (high
values of R
2
, low values of S).
2.4 Hysteresis Thresholding and Global
Analysis
Due to the local nature of the plane model (see Sub-
section 2.1), any detector based on this model can also
generate a high response for structures different from
planar structures. For that reason, it is important to
incorporate “global information” to discern true pla-
nar structures from these others. The stages in this
subsection are introduced for this purpose.
First, thresholding is applied to P in order to dis-
card voxels unlikely belonging to planar structures.
Hysteresis thresholding has been shown to outper-
form the standard thresholding algorithm (Sandberg,
2007). Here two thresholds are used, the large valuet
u
undersegments the volume whereas the other t
o
over-
segments it. Starting from the undersegmented vol-
ume (seed voxels), adjacent voxels are added to the
segmented volume by progressively decreasing the
threshold until the oversegmenting level t
o
is reached.
Here we have increased the robustness of hystere-
sis thresholding by constraining the selection of seeds
to the particular characteristics of planar structures
in experimental biomedical datasets, namely the rela-
tively high number of voxels connected. So, we have
introduced two additional thresholds so that seed vox-
els belonging to components with less than t
a
pixels
slicewise, or t
h
in 3D, are discarded. This allows iso-
lation of seeds that are most representative of planar
structures, thus improving the global performance.
Finally, a global analysis stage intends to iden-
tify the segmented components that are actually pla-
nar structures. A distinctive attribute is their relatively
large dimensions. Therefore, the size (i.e. the num-
ber of voxels of the component) can serve as a ma-
jor global descriptor. A threshold t
v
(similar or equal
to t
h
) is then introduced to set the minimal size for a
component to be considered as a planar structure.
3 EXPERIMENTAL RESULTS
To illustrate the performance of the algorithm, it was
tested with several volumes taken under different ex-
perimental conditions and with several bioimaging
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
44
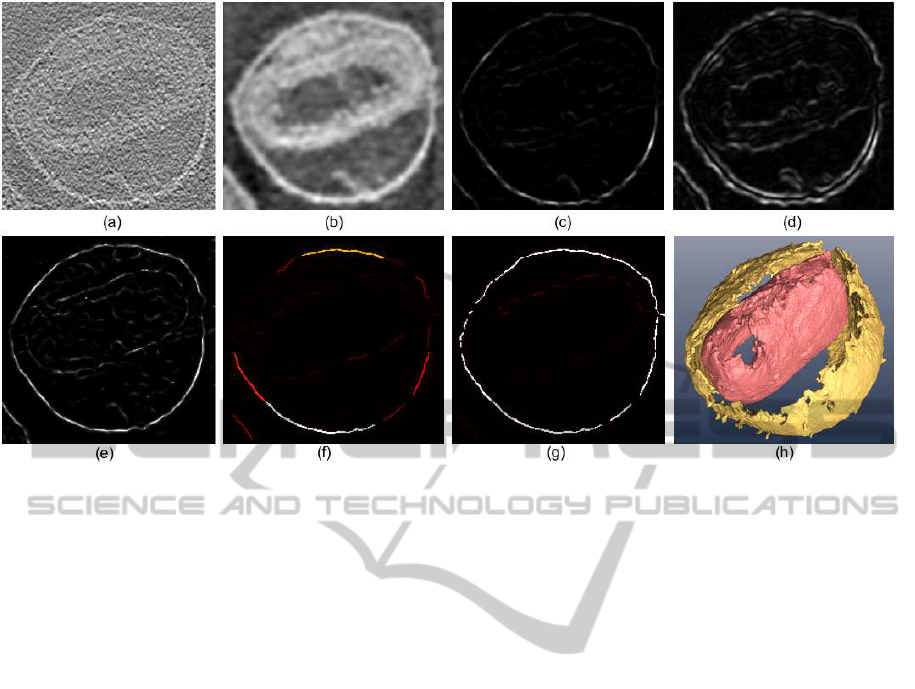
Figure 3: The procedure applied to a volume of Vaccinia virus obtained by electron tomography. (a) slice of the original
volume. (b) at a scale σ = 3. (c-e) R, S and P, respectively. (f, g) hysteresis thresholding. seed voxels to extract the outer
membrane after the t
a
and after t
h
thresholding, respectively. brighter colour means larger number of connected voxels. (h)
Membranes detected after the global analysis. The membrane of the internal core (in pink) was obtained after running the
algorithm at a scale of σ = 6.
techniques. The volumes were rescaled to a common
density range of [0, 1]. The optimal results were ob-
tained using the same basic parameter configuration
for hysteresis thresholding, in particular t
u
∈[0.35,1],
t
o
∈ [0.05,0.4] and t
a
∈ [15, 35]. The values of the
parameters σ, t
l
, t
h
and t
v
, however, depend on the
specific dataset and were readily set by inspection of
the volume. σ is the thickness of the sought planes,
which were membranes in most of our tests.
First, to show the procedure at work, Fig. 3 shows
the different stages applied to a volume of Vaccinia
virus (Cyrklaff et al., 2005). This volume was ob-
tained by electron tomography under low electron
dose and cryogenic temperatures, which makes it par-
ticularly noisy and with low contrast. The algorithm
succeeds in segmenting both the outer and the inter-
nal core membrane by properly tuning the parame-
ter σ. A scale of σ = 3 was applied to extract the
outer membrane. For the core membrane, however, a
much higher value was necessary (σ = 6) because this
membrane actually comprises two layers that make it
rather thick, thereby needing a higher scale to extract
it separately.
Fig. 3(c-e) (which were obtained at σ = 3, tar-
geting at the outer membrane) clearly shows that,
though the gauge R actually quantifies the level of
local membrane-ness, it still depends on the density
level. Thus, there are some parts of the membrane
where R exhibits weak values. On the contrary, P
only contains differential information and, therefore,
higher strength is shown throughoutthe membrane re-
gardless of the density value. However, the side ef-
fect is that other structures resembling planes at local
level also produce a high value of P (for instance, the
dense material between the outer membrane and the
core seen at the top of (e); or the fiber attached to the
internal side of the outer membrane seen at the bottom
of (e)). The hysteresis thresholding procedure and the
global analysis then manage to extract the true mem-
branes. This behaviour is an inherent feature of the
algorithm.
To further illustrate the performance of the algo-
rithm, it was applied to several volumes obtained by
electron tomography and using experimental condi-
tions that provides better contrast than in the pre-
vious case. The volumes contained different spec-
imens, namely vesicles, mitochondrion and chloro-
plast, respectively. Fig. 4 shows a gallery of the
structures, mostly membranes, detected by the algo-
rithm. The algorithm was run at a scale σ of 2,
1.5 and 0.1, respectively. As shown, all the planar
structures present in the volumes were clearly iden-
tified and come out of the background. The datasets
were taken from the CCDB (Cell-Centered DataBase,
http://ccdb.ucsd.edu) (Martone et al., 2008).
Finally, in order to demonstrate the applicabil-
SEGMENTATION OF PLANAR STRUCTURES IN BIOIMAGING
45

Figure 4: Planar structures detected by the algorithm for three different volumes containing vesicles, mitochondrion and
chloroplast, respectively, that were obtained by electron tomography. Top: a slice of the original volume is shown. Bottom:
3D visualization.
Figure 5: Planar structures detected by the algorithm for three representative areas of a thick retina tissue. Top: a slice of the
original volume is shown. Bottom: 3D visualization of the planar structures.
ity of the algorithm to other bioimaging disciplines,
we applied it to a volume derived from a study con-
sisting in the ultrastructural characterization of the
mouse optic nerve head and retina (Kim et al., 2010;
Nguyen et al., 2011), which was taken from the
CCDB database (Martone et al., 2008). In this study,
the thick tissue section was subjected to 3D recon-
struction by a technique known as ’Serial Block Face
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
46

SEM’ (SBFSEM). Here the tissue is progressively
sliced into thin sections and the face of the remain-
ing block is imaged by means of a Scanning Elec-
tron Microscope (SEM). At the end of the process,
the images that were taken are stacked into a single
volume, hence the 3D reconstruction. The tissue that
was studied here contained different nerve cell lay-
ers. Figure 5 shows a gallery of representative areas
of the different layers, where the segmentation of the
planar structures performed by our algorithm is appar-
ent. For these cases, the scale used in the application
of the algorithm was 0.5.
4 CONCLUSIONS
We have presented a procedure to detect planar struc-
tures in volumes obtained by different bioimaging
techniques. It relies on a simple local model for a
plane and on the local differential structure to deter-
mine points whose neighbourhood resembles plane-
like features. Later stages of the algorithm then intend
to definitely determine which of those points do actu-
ally constitute the planar structures. The performance
of algorithm has been shown on a set of representative
volumes. In general, the algorithm has turned out to
be effective to detect planar structures, often found in
biological datasets. Therefore, it has potential to be a
useful tool for (semi-)automated interpretation of 3D
volumes obtained by different bioimaging technolo-
gies.
ACKNOWLEDGEMENTS
Work supported by grants MCI-TIN2008-01117 and
JA-P10-TIC6002. A.M.S. is a fellow of the Spanish
FPI programme.
REFERENCES
Chandler, D. and Roberson, R. W. (2009). Bioimaging:
current techniques in light and electron microscopy.
Jones and Barlett Pub.
Cyrklaff, M., Risco, C., Fernandez, J. J., Jimenez, M. V.,
Esteban, M., Baumeister, W., and Carrascosa, J. L.
(2005). Cryo-electron tomography of vaccinia virus.
Proc. Natl. Acad. Sci. USA, 102:2772–2777.
Fernandez, J. J. and Li, S. (2003). An improved algorithm
for anisotropic diffusion for denoising tomograms. J.
Struct. Biol., 144:152–161.
Fernandez, J. J. and Li, S. (2005). Anisotropic nonlinear
filtering of cellular structures in cryoelectron tomog-
raphy. Comput. Sci. Eng., 7(5):54–61.
Florack, L. J., Romeny, B. H., Koenderink, J. J., and
Viergever, M. A. (1992). Scale and the differential
structure of images. Image and Vision Computing,
10:376–388.
Frangi, A., Niessen, W., Vincken, K., and Viergever, M.
(1998). Multiscale vessel enhancement filtering. Lec-
ture Notes in Computer Science, 1496:130–137.
Frank, J., editor (2006). Electron tomography. Springer.
Kim, K., Ju, W., Hegedus, B., Gutmann, D., and Ellisman,
M. (2010). Ultrastructural characterization of the op-
tic pathway in a mouse model of neurofibromatosis-1
optic glioma. Neuroscience, 170:178–188.
Koenderink, J. J. (1984). The structure of images. Biol.
Cybern., 50:363–370.
Lindeberg, T. (1990). Scale-space for discrete signals. IEEE
Trans. PAMI, 12(3):234–254.
Lindeberg, T. (1998). Edge detection and ridge detection
with automatic scale selection. Int. J. Computer Vi-
sion, 30:117–154.
Lucic, V., Forster, F., and Baumeister, W. (2005). Struc-
tural studies by electron tomography: from cells to
molecules. Ann. Rev. Biochem., 74:833–865.
Martinez-Sanchez, A., Garcia, I., and Fernandez, J. (2011).
A differential structure approach to membrane seg-
mentation in electron tomography. J. Struct. Biol.,
175:372–383.
Martone, M., Tran, J., Wong, W. W., Sargis, J., Fong, L., ans
S. P. Lamont, S. L., Gupta, A., and Ellisman, M. H.
(2008). The cell centered database: An update on
building community resources for managing and shar-
ing 3D imaging data. J. Struct. Biol., 161:220–231.
Nguyen, J., Soto, I., Kim, K., Bushong, E., Oglesby, E., Va-
liente, F., Yang, Z., Davis, C., Bedont, J., Son, J., Wei,
J., Ellisman, M., and Marsh, N. (2011). Myelination
transition zone astrocytes are constitutively phago-
cytic and have synuclein dependent reactivity in glau-
coma. Proc. Natl. Acad. Sci. USA, 108:1176–1181.
Sandberg, K. (2007). Methods for image segmentation
in cellular tomography. Methods in Cell Biology,
79:769–798.
Volkmann, N. (2010). Methods for segmentation and in-
terpretation of electron tomographic reconstructions.
Methods Enzymol., 483:31–46.
Witkin, A. P. (1983). Scale-space filtering. In Proc. 8th Intl.
Conf. Artif. Intell., pages 1019–1022.
Young, I. T. and van Vliet, L. J. (1995). Recursive imple-
mentation of the gaussian filter. Signal Processing,
44:139–151.
SEGMENTATION OF PLANAR STRUCTURES IN BIOIMAGING
47
