ITERATIVE IMAGE INTERPOLATION FOR IRREGULARLY

SAMPLED IMAGE

Jonghwa Lee

and Chulhee Lee

Samsung Electronics Co., Ltd., San 24 Neonseo-Dong, Yongin-City, Gyeonggi-Do, Korea

Department Electrical and Electronic Engineering, Yonsei Univiversity

134 Shinchon-Dong, Seodaemun-Gu, Seoul, Korea

Keywords: Irregular Sampling, Wavelet Shrinkage, Iterative Interpolation.

Abstract: For irregularly sampled color images, an iterative interpolation algorithm utilizing a wavelet shrinkage

denoising technique is proposed. Exploiting the non-local information from neighboring blocks, the

reconstruction performance converges as the iteration of the proposed algorithm is repeated. Experimental

results show that the proposed algorithm outperforms the conventional algorithms in terms of subjective

quality and objective measures. The proposed algorithm correctly reconstructs the edge and provides

perceptually good performance with randomly chosen 25% pixels.

1 INTRODUCTION

Irregularly sampled signals can be found in many

application areas such as seismic data (Duijndam,

2001); (Herrmann, 2008) and medical imagery

(Lustig, 2007); (Lustig, 2008). The reconstruction

algorithms for irregularly sampled signals can be

divided into two groups: nonlinear algorithms, and

iterative algorithms. The nonlinear interpolation

methods have been proposed to solve the problem in

the early 1990s (Marvasti, 1987); (Marvasti, 1993).

One of such nonlinear algorithms is the Delaunay

triangulation method (Delaunay, 1934);

(Lertrattanapanich, 2004). Recent kernel regression

algorithms also provide a data adaptive filtering

algorithm (Takeda, 2006); (Takeda, 2007).

However, these methods apply low-pass filtering to

observed samples and produced poor results due to

blurring artifacts.

The iterative recovery method has been proposed

by Wiley (Wiley, 1978) which requires low-pass

filtering of unequally spaced samples. For band-

limited signals, under some restrictions the

irregularly sampled signals can recover the missing

signals after iterations (Sandberg, 1963). However,

these restrictions cannot be satisfied in general. The

recent framework using sparsity constraints and

iterative estimation produced improved performance

(Guleryuz, 2006a); (Guleryuz, 2006b). Li proposed

an iterative interpolation algorithm for irregularly

sampled signals utilizing this framework and the

block-matching based denoising algorithm (Li,

2008).

However, in (Li, 2008), the transform based

denoising algorithm usually produces the

undesirable artifacts in a flat area since the denoising

algorithm fails to consider edge information. Even

though the flat area has no edges, ringing artifacts

are produced in the originally homogeneous region.

This error-prone area can be localized using an edge

detection algorithm, and the smoothing algorithm

can be applied to the localized area. In the proposed

method, the block-based transform based denoising

algorithm with some modification is applied and the

non-local means algorithm (Buades, 2005) is used to

remove the ringing artifacts in flat areas.

2 PREVIOUS WORKS

Suppose a two dimensional plane and the scattered

points in the plane. For a set of points, drawing lines

from each point to its nearest points form a set of

vertices. These triangular patches include no

intersection from the other lines. This triangulation

is commonly known as Delaunay triangulation. It is

well known that the Delaunay triangulation is a

geometrically dual with a Voronoi diagram in

In other words, the Voronoi tessellation has the

intersection lines normal to the Delaunay

176

Lee J. and Lee C..

ITERATIVE IMAGE INTERPOLATION FOR IRREGULARLY SAMPLED IMAGE.

DOI: 10.5220/0003821701760181

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 176-181

ISBN: 978-989-8565-03-7

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

triangulation (Delaunay, 1934); (Lertrattanapanich,

2004). For 2-D signals, there exists fast algorithms

to form the Delaunay triangulation which has the

maximized minimum angle of each triangle over the

ordered sets of all triangulations, and the Delaunay

triangulation is known to be suitable for image

interpolation (Lertrattanapanich, 2004). In Qhull

algorithm (Barber, 1996), the Delaunay triangulation

is computed with sparsely observed 2-D samples.

Fig. 1 shows irregularly sampled and interpolated

images using the Delaunay triangulation with cubic

polynomials.

(a)

(b)

Figure 1: The Delaunay triangulation interpolation for the

irregularly sampled image: (a) the observed image (25%)

(b) the interpolated image.

Fig. 1 shows that the Delaunay interpolation

algorithm fails to correctly restore the edges around

the roof in the house and also produces severe noises

in a homogeneous region.

A recent algorithm improved the reconstructed

image using an iterative procedure (Li, 2008). In this

algorithm, the block matching and 3-D filtering

algorithm (BM3D) is used (Dabov, 2007). The

BM3D denoising method collects a group of non-

local blocks similar to the current block and stacks

them in 3-D arrays. The stacked 3-D arrays are

transformed using a transform technique (e.g., DCT

and wavelet), and the transform coefficients are

filtered using the shrinkage of transform spectrum or

thresholding operator. Then, the inverse transform is

applied. In the patch-based interpolation method (Li,

2008), the BM3D algorithm is used as the sparsity

constraints and the observed pixels are put back into

the resulting image (Abma, 2006); (Guleryuz,

2006a); (Guleryuz, 2006b).

3 PROPOSED INTERATIVE

INTERPOLATION

The proposed image interpolation algorithm for the

irregularly sampled signals exploits the concept of

the Guleryuz’s method and the BM3D (Dabov, 2007)

similar to the patch-based interpolation method (Li,

2008). The overall procedure of the proposed

algorithm is shown in Fig. 2. In the BM3D block,

the wavelet shrinkage algorithm (Chambolle, 1998);

(Donoho, 2006); (Donoho1995) was used. In

addition, the SSIM metric (Wang, 2004) was used to

find similar blocks and a Gaussian kernel was used

in computing the resulting image. In particular, the

proposed algorithm successfully removed some

undesirable artifacts in a flat area by excluding

neighboring blocks, which are substantially different

from the current block, in computing the weighted

average.

In the initial interpolation, the Delaunay

triangulation based interpolation is performed to

estimate the missing pixels using the observed

neighboring pixels. Since the Delaunay triangulation

based interpolation uses a cubic interpolation kernel

to estimate the missing pixels, blurred edges and

stained areas usually appear. Then, a modified

BM3D is applied, where the wavelet shrinkage

algorithm (Chambolle, 1998); (Donoho, 2006);

(Donoho1995) was used.

After similar blocks are collected, the blocks are

stacked together to form a cube. In the 3D wavelet

denoising method, a 3-D additive wavelet transform

(or over-complete wavelet transform) is applied to

the stacked blocks. Then, thresholding is applied to

the wavelet coefficients.

In this process, the coefficients smaller than the

threshold are set to zero. It is noted that the threshold

value is set to 30. After the inverse 3-D wavelet

transform is applied, the weights for aggregation of

the stacked blocks are computed. Then, the stacked

blocks produced by the wavelet shrinkage algorithm

are averaged and the Gaussian kernel.

ITERATIVE IMAGE INTERPOLATION FOR IRREGULARLY SAMPLED IMAGE

177

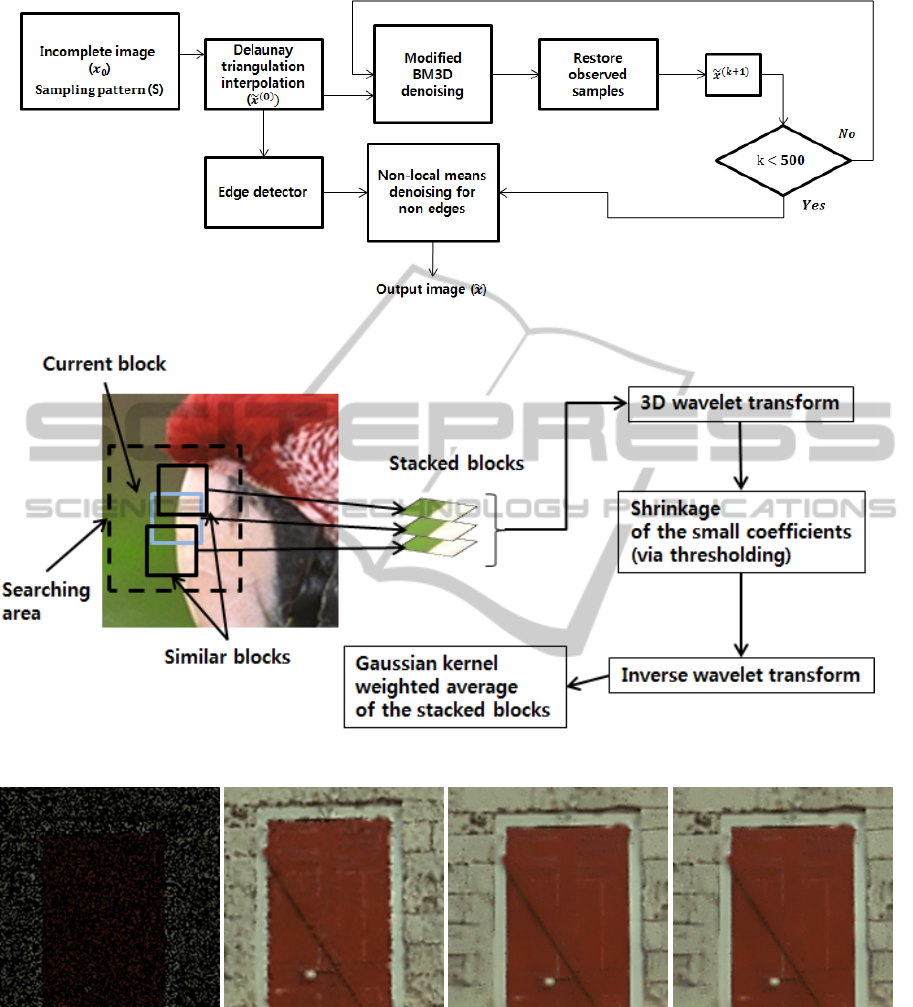
Figure 2: The overall procedure of the proposed algorithm.

Figure 3: Modified BM3D with wavelet shrinkage denoising.

(a) (b) (c) (d)

Figure 4: The parts of the results as the iteration is performed: (a) the observed image (25%) (b) the initial interpolation (c)

the fifth iteration (d) the 100th iteration.

This modified BM3D method is applied to every

pixel. Due to the 3D wavelet transform, the observed

pixels are also modified in the output of the

modified BM3D method. Thus, the observed pixels

are placed back into the output of the modified

BM3D method.

As the iteration (modified BM3D followed

injecting the observed samples) is repeated, the

edges with noises or the stained areas are cleaned as

shown in Fig. 4. However, the resulting image still

contains undesirable artifacts in a flat area and

produces ringing artifacts in the homogeneous

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

178

region. This is caused by some blocks which are

substantially different from the current block.

(a) (b)

Figure 5: The results after denoising: (a) image before

denoising (b) image after denoising (c) image before

denoising (d) image after denoising.

To address this problem, after applying an edge

detection operator to the initial interpolation image,

a modified non-local means (NLM) denoising

algorithm (Buades, 2005) is applied on the

homogeneous region. In the proposed algorithm, the

Laplacian of Gaussian (LoG) edge detector is used

to find edge positions (Chen, 1987).

The non-local means algorithm (Buades, 2005)

utilizes the similarity between two blocks which is

measured as a decreasing function of the weighted

Euclidean distance and the NLM algorithm uses the

weighted average of the center pixels in the

neighboring blocks for the current center pixel in the

current block.

However, it is more desirable that some

neighboring blocks are excluded in computing the

weighted average because some blocks are

substantially different from the current block.

Therefore, in the proposed method, SSIM values

between the current block and neighboring blocks

are computed and only the blocks whose SSIM

value is greater than 0.8 were used. This routine

successfully removed the ringing artifacts in the

homogeneous region as shown in Fig. 5.

Table 1: PSNR results for processing single channel

independently.

Images Delaunay SKR PBI Proposed

Kodim01 23.40 23.28 25.14

25.29

Kodim02 30.45 30.44 31.60

31.95

Kodim03 31.39 31.51 32.79

33.57

Kodim04 30.62 30.24 31.56

31.88

Kodim05 23.39 23.33

24.67

24.65

Kodim06 25.00 24.86

26.63

26.47

Kodim07 30.13 29.92 31.61

31.63

Kodim08 21.01 21.21 23.97

24.29

Kodim09 29.33 29.70 31.33

31.70

Kodim10 29.34 29.38 30.82

31.38

Kodim11 26.52 26.46

27.79

27.67

Kodim12 30.23 30.39 32.34

32.73

Kodim13 21.33 21.02

21.44

21.16

Kodim14 26.26 25.83

27.00

26.91

Kodim15 29.02 29.90 31.21

31.52

Kodim16 28.88 28.60 30.37

30.65

Kodim17 29.02 29.04

29.98

29.89

Kodim18 24.99 24.74

25.39

25.14

Kodim19 25.18 24.97 28.25

29.50

Kodim20 28.41 28.09 29.93

30.13

Kodim21 25.75 25.47 26.57

26.45

Kodim22 27.70 27.39 28.62

28.83

Kodim23 31.74 31.53 32.76

33.28

Kodim24 23.91 23.57

24.54

24.30

Average 27.21 27.12 28.60

28.79

4 EXPERIMENTAL RESULTS

AND DISCUSSIONS

In this paper, the proposed irregular interpolation

method is compared with three conventional

methods: the Delaunay method, the steering kernel

regression (SKR) method (Takeda, 2006); (Takeda,

2007), and the patch-based interpolation (PBI)

method (Li, 2008). Table 1 shows the PSNR results.

It is noted that the proposed interpolation algorithm

for the irregularly sampled image outperforms the

conventional interpolation algorithms on average.

Figs. 6 – 7 show visual comparison of some sub-

images: KODIM03 and KODIM10. Figs. 6 – 7 show

that the proposed interpolation algorithm recovers

the original images from the irregularly sampled

image with high quality, and the proposed algorithm

provides visually pleasing results. From Fig. 6, there

are several edge distortions (the yellow cap) in the

results of the Delaunay and the PBI methods, while

ITERATIVE IMAGE INTERPOLATION FOR IRREGULARLY SAMPLED IMAGE

179

the SKR and proposed methods restore the edges

better than the other methods. However, the SKR

method produces severe blurring, while the proposed

algorithm produces better results. In Fig. 7, the

diagonal edges exist along the yacht’s sail and the

proposed algorithm reconstructs the diagonal edges

with high quality.

(a) (b)

Figure 6: The visual comparison using KODIM03: (a) the

original image (b) the SKR method (c) the PBI method (d)

the proposed algorithm.

(a) (b)

Figure 7: The visual comparison using KODIM10: (a) the

original image (b) the SKR method (c) the PBI method (d)

the proposed algorithm.

REFERENCES

Abma, R. and N. Kabir, "3D interpolation of irregular data

with a POCS algorithm," Geophysics, vol. 71, pp.

E91-E97, 2006.

Barber, C. B., et al., "The Quickhull algorithm for convex

hulls," ACM Trans. Mathematical Software, vol. 22,

pp. 469-483, 1996.

Buades, A., et al., "A non-local algorithm for image

denoising," in IEEE Computer Vision and Pattern

Recognition, pp. 60-65, 2005.

Chambolle, A., et al., "Nonlinear wavelet image

processing: variational problems, compression, and

noise removal through wavelet shrinkage," IEEE

Trans. Image Process., vol. 7, pp. 319-335, 1998.

Chen, J. S., et al., "Fast Convolution with Laplacian-of-

Gaussian Masks," IEEE Trans. Patt. Anal. Mach.

Intell., vol. PAMI-9, pp. 584-590, 1987.

Dabov, K., et al., "Image Denoising by Sparse 3-D

Transform-Domain Collaborative Filtering," IEEE

Trans. Image Process., vol. 16, pp. 2080-2095, 2007.

Delaunay, B., "Sur la sphère vide, Izvestia Akademii Nauk

SSSR, Otdelenie Matematicheskikh i Estestvennykh

Nauk," vol. 7, pp. 793-800, 1934.

Donoho, D. L. and I. M. Johnstone, "Adapting to

Unknown Smoothness Via Wavelet Shrinkage,"

Journal of the American Statistical Association, vol.

90, 1995.

Donoho, D. L., "Compressed sensing," IEEE Trans.

Information Theory, vol. 52, pp. 1289-1306, 2006.

Duijndam, A. J. W., et al., "Irregular and sparse sampling

in exploration seismology," in Nonuniform sampling:

theory and practice, F. Marvasti, Ed., ed: Kluwer

Academic/Plenum, 2001.

Guleryuz, O. G., "Nonlinear approximation based image

recovery using adaptive sparse reconstructions and

iterated denoising-part I: theory," IEEE Trans. Image

Process., vol. 15, pp. 539-554, 2006.

Guleryuz, O. G., "Nonlinear approximation based image

recovery using adaptive sparse reconstructions and

iterated denoising-part II: adaptive algorithms," IEEE

Trans. Image Process., vol. 15, pp. 555-571, 2006.

Herrmann, F. J. and G. Hennenfent, "Non-parametric

seismic data recovery with curvelet frames,"

Geophsical Journal International, vol. 173, pp. 233-

248, 2008.

Lertrattanapanich, S. and N. K. Bose, "High resolution

image formation from low resolution frames using

Delaunay triangulation," IEEE Trans. Image Process.,

vol. 11, pp. 1427-1441, 2002.

Li ,X., "Patch-based image interpolation: algorithms and

applications," presented at the Int'l Workshop on Local

and Non-Local Approximation in Image Processing,

2008.

Lustig, M., et al., "Compressed Sensing MRI," IEEE

Signal Process. Mag., vol. 25, pp. 72-82, 2008.

Lustig, M., et al., "Sparse MRI: The application of

compressed sensing for rapid MR imaging," Magnetic

Resonance in Medicine, vol. 58, pp. 1182-1195, 2007.

Marvasti, F., "nonuniform sampling," in Advanced topics

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

180

in Shannon sampling and interpolation theory R. J. M.

II, Ed., ed: Springer-Verlag in NY, 1993.

Marvasti, F., A unified approach to zero-crossings and

nonuniform sampling of single and multi-dimensional

signals and systems: Chicago, Ill., 1987.

Sandberg, I. W., "On the Properties of Some Systems that

Distort Signals-I," Bell Syst. Tech. J., pp. 2003-2046,

1963.

Takeda, H. et al., "Kernel Regression for Image

Processing and Reconstruction," IEEE Trans. Image

Process., vol. 16, pp. 349-366, 2007.

Takeda, H. et al., "Robust Kernel Regression for

Restoration and Reconstruction of Images from Sparse

Noisy Data," in IEEE Int'l Conf. Image Processing,

pp. 1257-1260, 2006.

Wang, Z. et al., "Image quality assessment: from error

visibility to structural similarity," IEEE Trans. Image

Process., vol. 13, pp. 600-612, 2004.

Wiley, R., "Recovery of Bandlimited Signals from

Unequally Spaced Samples," IEEE Trans. Commun.,

vol. 26, pp. 135-137, 1978.

ITERATIVE IMAGE INTERPOLATION FOR IRREGULARLY SAMPLED IMAGE

181