A BIO-INSPIRED LEARNING AND CLASSIFICATION METHOD
FOR SUBCELLULAR LOCALIZATION OF A PLASMA
MEMBRANE PROTEIN
Wafa Bel Haj Ali
2
, Paolo Piro
1
, Lydie Crescence
3
, Dario Giampaglia
2
,
Oumelkheir Ferhat
3
, Jacques Darcourt
3
, Thierry Pourcher
3
and Michel Barlaud
2
1
Italian Institute of Technology (IIT), Genoa, Italy
2
I3S/CNRS Laboratory, University of Nice-Sophia Antipolis, Nice, France
3
Team Tiro CEA, University of Nice-Sophia Antipolis/CAL, Nice, France
Keywords:
Cell Classification, Sodium Iodide Symporter, Bio-inspired, k-NN, Boosting, Machine Learning.
Abstract:
High-content cellular imaging is an emerging technology for studying many biological phenomena. statistical
analyses on large populations (more than thousands) of cells are required. Hence classifying cells by experts
is a very time-consuming task and poorly reproducible. In order to overcome such limitations, we propose
an automatic supervised classification method. Our new cell classification method consists of two steps: The
first one is an indexing process based on specific bio-inspired features using contrast information distributions
on cell sub-regions. The second is a supervised learning process to select prototypical samples (that best
represent the cells categories) which are used in a leveraged k-NN framework to predict the class of unlabeled
cells. In this paper we have tested our new learning algorithm on cellular images acquired for the analysis
of changes in the subcellular localization of a membrane protein (the sodium iodide symporter). In order to
evaluate the automatic classification performances, we tested our algorithm on a significantly large database
of cellular images annotated by experts of our group. Results in term of Mean Avarage Precision (MAP) are
very promising, providing precision upper than 87% on average, thus suggesting our method as a valuable
decision-support tool in such cellular imaging applications. Such supervised classification method has many
other applications in cell imaging in the areas of research in basic biology and medicine but also in clinical
histology.
1 INTRODUCTION
High-content cellular imaging is an emerging technol-
ogy for studying many biological phenomena. Re-
lated cellular image analysis generally requires to
classify many cells according to their morphological
aspect, staining intensity, subcellular localization and
other parameters. Studied biological phenomena can
be heterogenous. For example, protein subcellular
localisation could depend on the expression of other
proteins or the cell states. In this case, statistical anal-
yses on large populations (more than thousands) of
cells are required. Furthermore, if time-lapse exper-
iments or drug screenings have to be performed nu-
merous different conditions have to be tested. New
powerful fully motorized microscopes are now able
to produce thousands of multiparametric images for
several experimental conditions. Consequently, large
numbers of cell images have to be analysed.
Unfortunately, humans are limited in their ability
to classify due to the huge amount of image data and
this makes the classification a burdensome task.
To circumvent this, we developed a new classifica-
tion method for the analysis of the staining morphol-
ogy of thousands (millions) of cells. First a fast mul-
tiparametric image segmentation algorithm extracts
cells with their nucleus. Next, our cell classifica-
tion method consists of two steps: The first one is an
indexing process based on specific bio-inspired fea-
tures using contrast information distributions on cell
sub-regions. The second is a supervised learning pro-
cess to select prototypical samples (that best represent
the cells categories) which are used in a leveraged k-
NN framework to predict the class of unlabeled cells.
Such classification method has many applications in
cell imaging in the areas of research in basic biology
and medicine but also in clinical histology.
In the present work, we used our classification
579
Bel Haj Ali W., Piro P., Crescence L., Giampaglia D., Ferhat O., Darcourt J., Pourcher T. and Barlaud M..
A BIO-INSPIRED LEARNING AND CLASSIFICATION METHOD FOR SUBCELLULAR LOCALIZATION OF A PLASMA MEMBRANE PROTEIN.
DOI: 10.5220/0003821905790584
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 579-584
ISBN: 978-989-8565-03-7
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

method to study the pathways that regulate plasma
membrane localization of the sodium iodide sym-
porter (NIS for Natrium Iodide Symporter). NIS is the
key protein responsible for the transport and concen-
tration of iodide from the blood into the thyroid gland.
NIS-mediated iodide uptake requires its plasma mem-
brane localization that is finely controlled by poorly
known mechanisms. For decades, the NIS-mediated
iodide accumulation observed in thyrocytes has been
a useful tool for the diagnosis (thyroid scintiscan) and
treatment (radiotherapy) of various thyroid diseases.
Improvements in radioablation therapy might result
from promoting targeting of NIS to the plasma mem-
brane in the majority of thyroid cancers or metas-
tases. NIS has also been described as a promiss-
ing therapeutic transgene promoting metabolic radio-
therapy (i.e., 131I uptake by cancer cells ectopically-
expressing NIS) in many different studies. An im-
portant improvement of this approach should benefit
from a better understanding of the post-transcriptional
regulation of NIS targeting to the plasma membrane,
Previously, we observed that mouse NIS catalyses
higher levels of iodide accumulation in transfected
cells compared to its human homologue. We showed
that this phenomenon was due to the higher density of
the murine protein at the plasma membrane. To reach
this conclusion, biologists classified several hundreds
of cells (Dayem et al., 2008). We have also demon-
strated, using a set of monoclonal antibodies, that hu-
man NIS is not expressed intracellularly in thyroid
and breast cancer (Peyrottes et al., 2009), as was pro-
posed by other groups. Our team is now focussing on
the analysis of NIS phosphorylation that most proba-
bly plays an important role in the post-transcriptional
regulation of the NIS. Using site-directed mutagene-
sis of previously-identified consensus sites, we have
recently shown that direct phosphorylation of NIS al-
ters NIS targeting to the plasma membrane, as well
as NIS recycling, causing retention of the protein in
intracellular compartments such as the Golgi appa-
ratus, the endoplasmic reticulum or the early endo-
somes. We used a high-content cellular imaging to
study the impact of the mutation of several putative
phosphorylation sites on the subcellular distribution
of the protein.
2 CLASSIFICATION METHOD
Our method for automatic classification of cell im-
ages is depicted as a block diagram in Fig. 1. The first
step is a pre-processing segmentation of cells from the
images. The database consist of two distinct paramet-
ric fluorescence images. The first one, called nucleus
Training
Bio-inspired
Descriptors
Training
database
Histogram of contrast-based
coefficients
CLASSIFICATION
Classification
Weighted Prototypes
SCORES
Testing
database
Bio-inspired
Descriptors
(a)
Training
Bio-inspired
Descriptors
Training
database
Histogram of contrast-based
coefficients
CLASSIFICATION
Classification
Weighted Prototypes
SCORES
Testing
database
Bio-inspired
Descriptors
(b)
Figure 1: Block diagram of the proposed method for auto-
matic cell classification: (a) cell segmentation step and (b)
descriptor extraction and classification process.
image shows the nucleus and the second called global
image, shows the staining of the proteine. Nucleus lo-
cations are detected from the nucleus image and used
as a prior for cell segmentation of the global image.
An example of both images and their segmentation
is shown in Fig. 2. Once cells are extracted, we ap-
ply our classification method ; First we compute bio-
inspired region descriptors, extracting contrast-based
features for each of the segmented cells. These de-
scriptors are then used in a supervised learning frame-
work where the most relevant prototypical samples
are used to predict the class of unlabeled cells.
We split this section in two parts: the first de-
scribes our feature extraction approach, whereas the
latter is focused on our prototype-based learning al-
gorithm.
2.1 Region based Bio-inspired
Descriptor
For better level of performance in differentiating be-
tween cells, it can be useful to get inspiration from the
way our visual system operates to analyze and repre-
sent the visual input. The first transformation under-
gone by a visual input is performed by the retina. In-
spired by the basic step of a retinal model, we define
bio-inspired features for image representation.
The basic idea is to use a descriptor inspired from
visual system model and specially from the main
characteristics of the retina processing. In fact, the
retinal cells are in a first stage sensitive to local dif-
ferences of illumination. This can be modeled by the
luminance contrast as for the BIF descriptors in (Bel
haj ali et al., 2011). Such descriptor is well adapted in
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
580

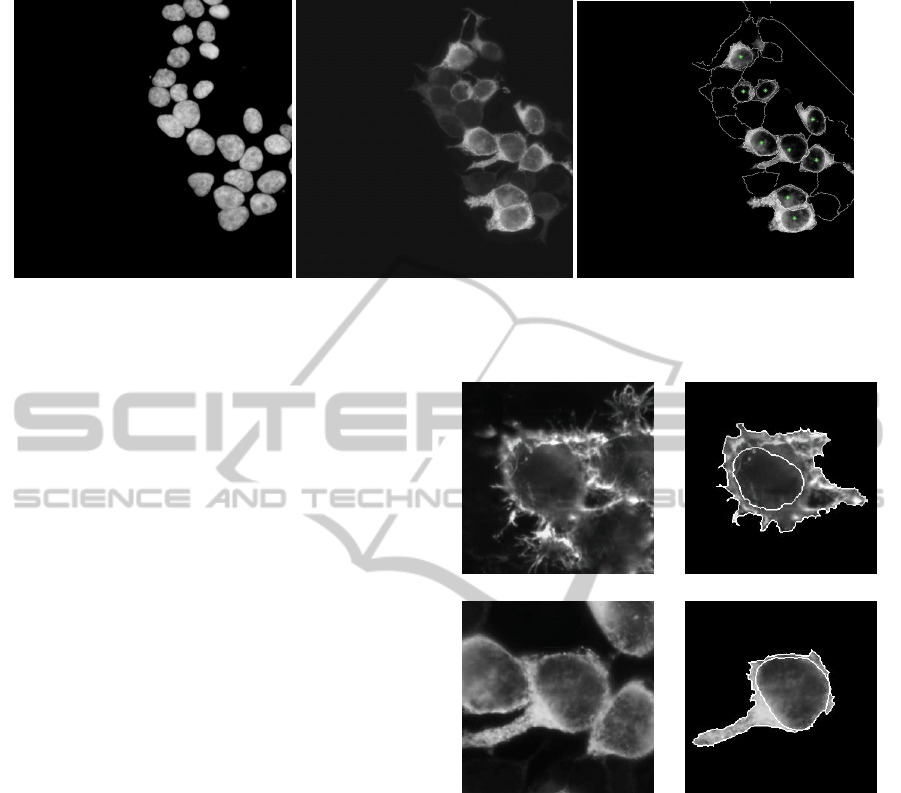
(a) (b) (c)
Figure 2: Image of the nucleus-staining of representative cells (a), NIS-specific immunostaining of the corresponding cells
(b) and their segmentation (c).
the case of our cells images since the most discrimi-
native visual feature between categories is the contrast
intensity of each region of the cell. Thus, we define
cell descriptors based on the local contrast in regions
of interest of each cell (nucleus, membrane and cyto-
plasm). The local contrast is obtained by a filtering
with Differences of Gaussians (DoGs) centered at the
origin. So that the contrast C
Im
for each position (x,y)
and a given scale s in the image Im is as follows:
C
Im
(x,y,s) =
∑
i
∑
j
(Im(i +x, j + y)·DoG
s
(i, j)). (1)
We used the DoGs described by (Field, 1994) where
the larger Gaussian has three times the standard de-
viation of the smaller one. After computing these
contrast coefficients in (1), we apply a non-linear
bounded transfer function, named neuron firing rates,
used in (Van Rullen and Thorpe, 2001). This function
is written as:
R(C ) = G · C /(1 + Re f · G ·C ), (2)
where G is named the contrast gain and Re f is known
as the refractory period, a time interval during which
a neuron cell reacts. The values of those two param-
eters proposed in (Van Rullen and Thorpe, 2001) to
best approximate the retinal system are G = 2000 Hz·
contrast
−1
and Re f = 0.005 s.
To extract our descriptors, we need to define
masks on cell images on which we encode firing rate
coefficients R(C ). According to the visual aspect of
cells, we split each cell into two regions of interest
as shown in Fig. 3, corresponding to nucleus and ex-
ternal part, by using simple morphological operators.
For both of them, firing rate coefficients are quanti-
fied into normalized L1 histograms of 32-bins then
concatinated, thus giving our global descriptor with a
dimension equal to 64.
Note that state of the art classical methods such as
SIFT descriptor encode gradient directions on square
(a)
(b)
Figure 3: An Mb (a) and an ER (b) extracted cells and their
two segmented regions of interest.
blocks (Lowe, 2004) and Gist features encode aver-
age energies of filters coefficients on square blocks
too (Oliva and Torralba, 2001).
2.2 Prototype-based Learning
We consider the multi-class problem of automatic cell
classification as multiple binary classification prob-
lems in the common one-versus-all learning frame-
work (Schapire and Singer, 1999). Thus, for each
class c, a query image is given a positive (negative)
membership with a certain confidence (classification
score). Then the label with the maximum score is as-
signed to the query.
We suppose given a set S of m annotated images.
A BIO-INSPIRED LEARNING AND CLASSIFICATION METHOD FOR SUBCELLULAR LOCALIZATION OF A
PLASMA MEMBRANE PROTEIN
581

Each image is a training example (x,y), where x is
the image feature vector and y =

−
1
C−1
,1

C
the
class vector that specifies the category membership
of the image. In particular, the sign of component y
c
gives the positive/negative membership of the exam-
ple to class c (c = 1,2,...,C), such that y
c
is negative
iff the observation does not belong to class c, positive
otherwise.
In this paper, we propose to generalize the classic
k-NN rule to the following leveraged multiclass clas-
sifier h
`
= {h
`
c
}:
h
`
c
(x
q
) =
T
∑
j=1
α
jc
K(x
q
,x
j
)y
jc
, (3)
where h
`
c
is the classification score for class c, x
q
de-
notes the query image, α
jc
the leveraging coefficients,
which provide a weighted voting rule instead of uni-
form voting, and K(·,·) is the k-NN indicator func-
tion:
K(x
i
,x
j
) =

1 , x
j
∈ NN
k
(x
i
)
0 , otherwise
, (4)
with NN
k
(x
i
) denoting the set of the k-nearest neigh-
bors of x
i
.
Training our classifier essentially consists in se-
lecting the most relevant subset of training data, i.e.,
the so-called prototypes, whose cardinality T is gen-
erally much smaller than the original number m of an-
notated instances. The prototypes are selected by first
fitting the coefficients α
j
, and then removing the ex-
amples with the smallest α
j
, which are less relevant
as prototypes.
In order to fit our leveraged classification rule (3)
onto training set S , we should try to directly minimize
the multiclass surrogate
1
(exponential) risk, which
is defined as the actual misclassification rate on the
training data, as follows:
ε
exp

h
`
c
,S

.
=
1
m
m
∑
i=1
exp
n
−ρ(h
`
c
,i)
o
. (5)
where:
ρ(h
`
c
,i) = y
ic
h
`
c
(x
i
) (6)
is the multiclass edge of classifier h
`
c
on training ex-
ample x
i
. This edge measures the “goodness of fit”
of the classifier on example (x
i
,y
i
) for class c, thus
being positive iff the prediction agrees with the ex-
ample’s annotation.
In order to solve this optimization, we propose
a boosting-like procedure, i.e., an iterative strategy
1
We call surrogate a function that upperbounds the risk
functional we should minimize, and thus can be used as a
primer for its minimization.
where the classification rule is updated by adding a
new prototype (x
j
,y
j
) (weak classifier) at each step t
(t = 1,2,. .., T ), thus updating the strong classifier (3)
as follows:
h
(t)
c
(x
i
) = h
(t−1)
c
(x
i
) + δ
j
K(x
i
,x
j
)y
jc
. (7)
( j is the index of the prototype chosen at iteration t.)
Using (7) into (6), and then plugging it into (5), turns
the problem of minimizing (5) to that of finding δ
j
with the following objective:
arg min
δ
j
m
∑
i=1
w
i
· exp

−δ
j
r
i j

. (8)
In (8), we have defined w
i
as the weighting factor,
depending on the past weak classifiers:
w
i
= exp
n
−y
ic
h
(t−1)
c
(x
i
)
o
, (9)
and r
i j
as a pairwise term only depending on training
data:
r
i j
= K(x
i
,x
j
)y
ic
y
jc
. (10)
Finally, taking the derivative of (8), the global mini-
mization of surrogate risk (5) gives the following ex-
pression of δ
j
:
δ
j
=
1
2
log
γ ·
∑
i:r
c
i j
>0
w
i
∑
i:r
c
i j
<0
w
i
, (11)
where γ is a coefficient that compensates for the class
imbalance.
We provided theoretical details and properties of
our boosting algorithm in (Piro et al., 2012), as well
as an extension of UNN to inherent multiclass classi-
fication in (Piro et al., 2010).
We also tried a “soft” version of the UNN classi-
fication rule, called UNN
s
, which considers a logistic
estimator for a Bernoulli prior that vanishes with the
rank of the neighbors, thus decreasing the importance
of farther neighbors:
ˆp( j) = β
j
=
1
1 + exp(λ( j − 1))
. (12)
This amounts to redefining (3) as follows:
h
`
c
(x
q
) =
T
∑
j=1
α
jc
β
j
K(x
q
,x
j
)y
jc
. (13)
(Notice that k-NN indexed by j are supposed to be
sorted from closer to farther.)
3 EXPERIMENTS
The images at 40-fold magnification were acquired
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
582

(a) (b)
Figure 4: A sample Mb cells image (a) and ER cells image (b).
by means of a fully fluorescence microscope (Zeiss
Axio Observer Z1) coupled to a monochrome digital
camera (Photometrics cascade II camera). The im-
ages have a resolution of 1024x1024 pixels,
In our biological experiments, we individually ex-
pressed different NIS proteins mutated for putative
sites of phosphorylation. The effect on the protein
localization of each mutation was studied after im-
munostaining using anti-NIS antibodies as previously
described (Dayem et al., 2008). Immunocytolocaliza-
tion analysis revealed three cell types with different
subcellular distributions of NIS: at the plasma mem-
brane; in intracellular compartment (mainly endo-
plasmic reticulum); throughout the cytoplasm (with
an extensive expression).
For this purpose, we collected 489 cell images of
such biological experiments and manually annotated
them according to the three classes, that are denoted
in the following as Mb protrusion and Mb (389 cells),
ER (100 cells) and Round (8 cells).
Since round cells are very easy to classify (very
high contrast everywhere in the cell), we focus on the
two category classification: Membrane (Mb) and ER.
An example of Mb and ER cells is given in Fig. 4.
We start by extracting our features on cells im-
ages. An important parameter for our bio-inspired
descriptors is the scale on which we compute the
local contrast. In fact, the standard deviations of
the DoG are dependant of this parameter as follows:
σ1 = 0.5 · 2
scale−1
and σ2 = 3 · σ1. We study first the
more relevant scale space and the evaluations on 100
experiments are reported in the curve of the Fig. 5.
Thus, according to those experiments the following
evaluations are performed using the scale 5 for de-
scriptors.
Once we get descriptors of all the cells in the
database, we ran our UNN algorithm by training on
50% of the images, while testing on the remaining
50%. In order to get robust performance estimation,
Figure 5: Average classification rate as a function of the
descriptors scale using UNN
s
.
we repeated the evaluation 100 times over different
random training/testing folds. Note that we used a
fast and effecient tool for the k-NN search provided
in the Yael toolbox
2
.
Our classification algorithm UNN
s
was evaluated
in a first step using a uniform regularization by the
mean of the parameter γ that compensates the class
imbalance. In a second step, we focused in an adap-
tive regularization according to majority and minority
classes and we denote this approach by UNN
s adaptive
.
This approach allows to have automatically a balance
number of trained prototypes per class (see Tab. 1)
and visibly decrease misclassification.
We report the average classification results and the
classification rate of each class in Tab. 2. Remark that
we achieve a mean average precision (MAP) greater
than 87.5% when using UNN
s adaptive
, which is a very
promising result for our cell descriptor and classifi-
cation method. Our classification approach improves
the MAP of the k-NN classifier of more 3% and the
SVM one of more than 11%. Moreover some mis-
2
Source code can be downloaded in the following link:
https://gforge.inria.fr/projects/yael
A BIO-INSPIRED LEARNING AND CLASSIFICATION METHOD FOR SUBCELLULAR LOCALIZATION OF A
PLASMA MEMBRANE PROTEIN
583

Table 2: Global average precision (MAP), average precision for Mb and average precision for ER for different classifiers.
mAP AP for Mb AP for ER
µ(mAP) σ(mAP) µ(AP) σ(AP) µ(AP) σ(AP)
k-NN 84.22 2.56 94.81 2.02 73.64 5.63
UNN
s
86.04 2.54 94.48 1.90 77.60 5.46
UNN
s adaptive
87.67 1.93 89.27 2.26 86.08 3.78
SVM 76.46 4.55 95.58 2.38 57.34 10.67
Table 1: This table shows the percentage of prototypes
number selected from the training set by both UNN
s
and
UNN
s adaptive
: We report the total number (N
t
), the one in
the class Mb (N
Mb
), and in the class ER (N
ER
). The distribu-
tion of selected prototypes on both classes is more balanced
using UNN
s adaptive
.
N
t
N
Mb
N
ER
UNN
s
69.24% 50.20% 19.03%
UNN
s adaptive
47.69% 28.58% 19.11%
classification arises on the minority class (ER) using
k-NN , thus giving an average precision (AP) of about
73% (see Tab. 2). Using UNN
s adaptive
classification
improved MAP of the minority class up to 86% thus
13% better than k-NN
˙
For the SVM classification, the
result in Tab. 2 shows that there is an important classi-
fication error on ER cells where the AP is about only
57%.
4 CONCLUSIONS
In this paper, we have presented a novel algorithm for
automatic segmentation and classification of cellular
images based on different subcellular distributions of
the NIS protein. First of all, our method relies on
extracting highly discriminative descriptors based on
bio-inspired histograms of Difference-of-Gaussians
(DoG) coefficients on cellular regions. Then, we
propose a supervised classification algorithm, called
UNN, for learning the most relevant prototypical
samples that are to be used for predicting the class of
unlabeled cellular images according to a leveraged k-
NN rule. We evaluated UNN performances on a sig-
nificantly large database of cellular images that were
manually annotated. Although being the very early
results of our methodology for such a challenging ap-
plication, performances are really satisfactory (aver-
age global precision of 87.5% and MAP of the mi-
nority class up to 86%) and suggest our approach as a
valuable decision-support tool in cellular imaging.
REFERENCES
Bel haj ali, W., Debreuve, E., Kornprobst, P., and Bar-
laud, M. (2011). Bio-Inspired Bags-of-Features for
Image Classification. In International Conference
on Knowledge Discovery and Information Retrieval
(KDIR 2011).
Dayem, M., Basquin, C., Navarro, V., Carrier, P., Marsault,
R., Chang, P., Huc, S., Darrouzet, E., Lindenthal, S.,
and Pourcher, T. (2008). Comparison of expressed
human and mouse sodium/iodide symporters reveals
differences in transport properties and subcellular lo-
calization. Journal of Endocrinology, 197(1):95–109.
Field, D. J. (1994). What is the goal of sensory coding?
Neural Computation, 6(4):559–601.
Lowe, D. G. (2004). Distinctive image features from scale-
invariant keypoints. International Journal of Com-
puter Vision, 60(2):91–110.
Oliva, A. and Torralba, A. (2001). Modeling the shape
of the scene: A holistic representation of the spatial
envelope. International Journal of Computer Vision,
42:145–175. 10.1023/A:1011139631724.
Peyrottes, I., Navarro, V., Ondo-Mendez, A., Marcellin, D.,
Bellanger, L., Marsault, R., Lindenthal, S., Ettore, F.,
Darcourt, J., and Pourcher, T. (2009). Immunoanalysis
indicates that the sodium iodide symporter is not over-
expressed in intracellular compartments in thyroid and
breast cancers. European Journal of Endocrinology,
160(2):215–25.
Piro, P., Nock, R., Nielsen, F., and Barlaud, M. (2010).
Multi-Class Leveraged k-NN for Image Classification.
In Proceedings of the Asian Conference on Computer
Vision (ACCV 2010).
Piro, P., Nock, R., Nielsen, F., and Barlaud, M. (2012).
Leveraging k-nn for generic classification boosting.
Neurocomputing, 80:3–9.
Schapire, R. E. and Singer, Y. (1999). Improved boosting al-
gorithms using confidence-rated predictions. Machine
Learning, 37:297–336.
Van Rullen, R. and Thorpe, S. J. (2001). Rate coding versus
temporal order coding: what the retinal ganglion cells
tell the visual cortex. Neural Comput, 13(6):1255–
1283.
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
584