
GPU-BASED VISUALIZATION OF HYBRID TERRAIN MODELS
E. G. Paredes
1
, M. B
´
oo
1
, M. Amor
2
, J. D
¨
ollner
3
and J. D. Bruguera
1
1
Centro de Investigaci
´
on en Tecnolog
´
ıas de la Informaci
´
on (CITIUS), University of Santiago de Compostela,
Santiago de Compostela, Spain
2
Dept. of Electronics and Systems, Univ. of A Coru
˜
na, A Coru
˜
na, Spain
3
Hasso-Plattner-Institut, University of Potsdam, Potsdam, Germany
Keywords:
Hybrid Terrain Models, GPU Rendering, Terrain Visualization, Tessellation.
Abstract:
Hybrid terrain models formed by a large regular mesh refined with detailed local TIN meshes represent an
interesting and efficient approach for the representation of complex terrains. However, direct rendering of the
component meshes would lead to overlapping geometries and discontinuities around their boundaries. The
Hybrid Meshing algorithm solves this problem by generating an adaptive tessellation between the boundaries
of the component meshes in real-time. In this paper, we present a highly parallel implementation of this
algorithm using the Geometry Shader on the GPU.
1 INTRODUCTION
Interactive visualization of Digital Terrains Models
(DTM) has been a common subject of research during
the last decade. However, the integration of data from
different sources is still a problematic question, al-
though new data collections are constantly being cre-
ated (Oosterom et al., 2008).
Hybrid terrain models present additional features
for the representation of DTMs, not existing in the
more common regular grid based Digital Elevation
Models (DEM) or Triangulated Irregular Networks
(TIN) models. Using hybrid models, a DTM can be
defined by the combination of regular grid-based ele-
vation data and some locally detailed TIN meshes of
the complete terrain surface representing complex ter-
rain features and artificial micro-structures like con-
structions or roads. Direct rendering of hybrid terrain
models, however, could generate meshes with holes
and geometric discontinuities between the borders of
the different parts.
The Hybrid Meshing (HM) algorithm (B
´
oo et al.,
2007) introduces a new method for combining the
TIN and grid meshes in a new coherent crack-free
model, for any LOD in the grid. This approach has re-
cently been extended to support multiresolution ren-
dering of both meshes (Paredes et al., shed).
In this paper, we present the GPU HM method, the
first implementation of a hybrid model renderer work-
ing at interactive frame rates into the GPU. Based on
the HM algorithm, our implementation uses Geom-
etry Shader (GS) technology to attain parallelism by
simultaneously running several GS threads perform-
ing the local tessellation of the models boundaries.
2 HM ALGORITHM
The HM algorithm achieves an efficient visualization
of hybrid terrain models formed by a multiresolution
regular grid and local high resolution TINs, as shown
in previous works (Paredes et al., 2009). In Figure
1(c) is depicted an example of the crack-free model
obtained from the union of the view-dependent refine-
ment of a multiresolution grid (see Figure 1(a)) and a
single-resolution TIN (see Figure 1(b)).
The algorithm joins the boundaries of both kind of
meshes following a local tessellation strategy inside
the multiresolution grid cells. The grid cells are clas-
sified as Non Covered (NC), Partially Covered (PC)
or Completely Covered (CC) cells, according to the
overlapping with the TIN mesh. During the visual-
ization, the visible grid cells in the extracted view-
dependent LOD of the grid are processed according
to their classification. Thus NC cells are rendered as
usual, CC grid cells are discarded since they will be
replaced by the detailed TIN mesh, and PC cells are
locally tessellated to join both meshes’ boundaries.
To simplify the adaptive tessellation of the cells,
the TIN boundary (TB) is locally convexified within
254
G. Paredes E., Bóo M., Amor M., Döllner J. and D. Bruguera J..
GPU-BASED VISUALIZATION OF HYBRID TERRAIN MODELS.
DOI: 10.5220/0003823302540259
In Proceedings of the International Conference on Computer Graphics Theory and Applications (GRAPP-2012), pages 254-259
ISBN: 978-989-8565-02-0
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

(a) (b) (c)
Figure 1: Hybrid terrain model example. (a) Base regular grid. (b) Detailed TIN component mesh. (c) Resulting hybrid model
with different components highlighted.
each cell in a preprocessing stage, and the result en-
coded in a unified grid LOD independent representa-
tion. Thus, the convexification triangles are decoded
during the visualization, while the remaining PC cells
tessellation triangles are easily generated on-the-fly.
2.1 Local Tessellation Algorithm
Two precomputed data structures are used to connect
the PC cell vertices and the convexified TIN boundary
inside PC cells: the Grid Classification (GC) list and
the list of PC cells (called Vertex Classification list in
the original HM article and renamed here for reasons
of clarity). The GC list stores the type (NC, CC, PC)
of each cell in the multiresolution grid mesh. The list
of PC cells contains the information used in the adap-
tive tessellation of each PC cell; i.e., the TB vertices
whose 2D projection falls into the grid cell area, and
the cell corner vertices not covered by the TIN mesh.
Since TB vertices and cell corner vertices are se-
quentially numbered, PC cell related data can be en-
coded as a 4-tuple {A, L, C, I}, where A is the first TB
vertex contained in the cell, L is the number of TB
vertices present in the cell, C is the first corner vertex
not covered by the TIN mesh, and I is the number of
uncovered corners in the cell. The cell tessellation is
achieved by generating corner triangles joining con-
secutive TB vertices to the uncovered corners of the
cell. Since the TB has been previously convexified
(see Section 2.2), the cell corner vertices can be safely
joined to consecutive TB vertices, shifting to the next
cell used as link point with the TIN boundary, when
the generated corner triangle overlaps the TIN.
2.2 Incremental Local Convexification
of TIN Boundary
To easily regenerate on demand the convexification
triangles for a given PC cell of any LOD, the HM al-
gorithm precomputes and encodes these triangles us-
ing a unified representation valid for every grid LOD.
The process begins by computing the convexifi-
cation of the TIN boundary in the PC cells at the
11
12
13
14
15
16
17
19
18
20
21
22
23
25
24
26
27
28
TIN
Figure 2: Incremental local convexification of the TB.
finest LOD. For each cell, the concave caves on the
TB convex hull are detected and triangulated using
any tessellation algorithm (Shewchuk, 1996). Fig-
ure 2 shows an example (represented in a top view)
where the TB convex hulls of the PC cells are de-
limited by vertices {11, 12, 15} (bottom right cell),
{15, 21, 22} (top right cell), {22, 26} (top left cell)
and {26, 27, 28} (bottom left cell). Once the TIN
boundary convexification at this LOD has finished,
the same process is repeated at the next coarser LOD
until the last one is reached. Since an incremental
convexification strategy is used, triangles generated in
this LOD are preserved in the convexification of the
next coarser LOD. In the same example of Figure 2,
the convex hull of the coarser level is defined by the
vertices {11, 28}.
The TB list represents the TIN boundary vertices
as a circular list stored in clockwise order. Associ-
ated to each boundary vertex there is an additional
connectivity value indicating the distance, counted in
number of vertices, between that vertex and the most
distant one connected to it in the convexified TB. If
vertex i has a connectivity value j, the farthest bound-
ary vertex connected to it in the convexified boundary
is i + j. Also note that the starting vertex of a cave is
connected to all the vertices in that cave, except for
the ones forming part of a nested sub cave. This uni-
fied representation works perfectly well for different
levels of detail, as explained in (B
´
oo et al., 2007).
GPU-BASED VISUALIZATION OF HYBRID TERRAIN MODELS
255

GPU Memory
TB List VBO
tb0
tb1 tb2
tb3
...
TB List
PC Cells VBO
pc0
pc1 pc2
pc3
...
PC List
GS
v0
v1 v2
v3
...
v0
v1 v2
v3
...
TIN
Grid
Geometry VBO
{
Vertex
attributes
TBO
TBO
Figure 3: Organization of data structures in memory.
3 GPU HM APPROACH
Our approach attains the parallel tessellation of sev-
eral PC cells by running multiple instances of the HM
algorithm in the GPU cores. Furthermore, an opti-
mized version of the original data structures is used
to improve the memory access.
In our proposal, Geometry Shaders are used to de-
code the precomputed data structures and to generate
the triangles needed for the tessellation of each PC
cell. The GPU parallelism is automatically exploited
as these tasks can be efficiently executed simultane-
ously in multicore GPUs.
Next, the optimized data structures and the tessel-
lation and rendering algorithm are presented.
3.1 GPU and CPU Data Structures
The data structures used by the original HM algorithm
were presented in Section 2: the GC list, the list of PC
cells and the TB list. Since in the GPU HM method
the rendering is performed by the Geometry Shader,
every shader thread needs to access some of these
structures and the meshes’ geometric data. The orig-
inal HM data layout, however, can not be efficiently
accessed from the GPU. Thus, we have modified the
data storage and accessing strategies depending upon
their accessing pattern. Figure 3 illustrates the loca-
tion and access methods used for the data structures.
The GC list is only needed to identify the cover-
age pattern of the cell for rendering the grid mesh.
Once the grid cell has been identified, it is rendered,
discarded or tessellated using the GPU and thus is not
needed by the Geometry Shader.
The GPU HM rendering algorithm uses the geo-
metric data of the TB vertices and the grid cell be-
ing tessellated, together with the TB data and the list
of PC cells. Consequently, these data structures have
to be maintained in GPU memory, stored in Vertex
Buffer Objects (VBO), although they are accessed
in different ways. The geometry data and the TB
list need an array-like access, since the processing
of one PC cell may involve reading non adjacent ele-
ments in random order. Texture Buffer Objects (TBO)
(OpenGL.org, 2009), associated to the correspond-
ing VBOs, are used in our proposal to read this data
within the shader. Using TBOs is an efficient way
to obtain array-like access to large data buffers in the
GPU memory. They provide a convenient interface to
the data, simulating a 1D texture where the tex coordi-
nate corresponds to the offset in the buffer object. Ad-
ditionally, accessing latencies can be effectively hid-
den by overlapping the readings with data processing
operations, since in the HM rendering stage there are
several processing operations.
An additional optimization to improve the data lo-
cality of the TB list has been used. The TIN mesh
vertices are ordered in the vertex buffer containing the
geometry data to guarantee that the TB boundary ver-
tices are stored at the beginning. In this way, the offset
of the vertex data in the buffer object represents its po-
sition in the TB list. Thus, vertex information can be
accessed by using its TB index –reducing one level of
indirection regarding to the original data structures–
and adjacent vertices in the TB are now adjacent in
the buffer object, improving the cache behavior due
to this better data locality.
The PC list, on the other hand, is made avail-
able to the shader through normal input vertex at-
tributes. There is a one-to-one relationship between
PC cells and vertex shader threads; therefore, packing
the items in the PC list as input vertex attributes is the
most effective way to send the right information for
every shader thread. Moreover, data transfer between
CPU and GPU during rendering is reduced, given that
we can use indexed draw calls to select the active PC
cells being tessellated every frame. This list of active
PC cells is easily built on-the-fly by the CPU accord-
ing to the view-dependent grid LOD, and efficiently
uploaded to the GPU due to its small size.
3.2 Rendering Algorithm
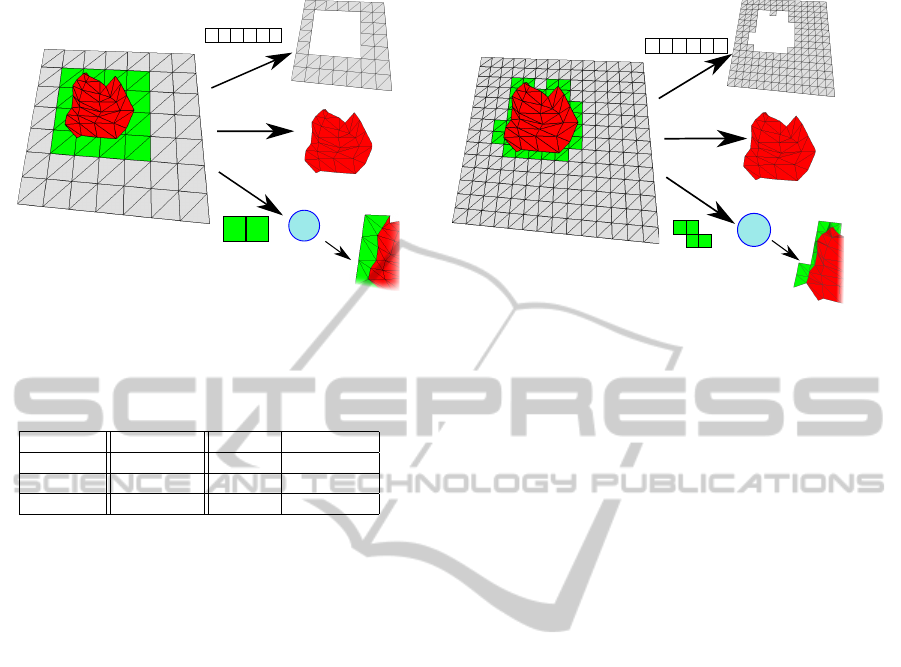
The GPU HM rendering steps are similar to the steps
of the original algorithm, but the implementation dif-
fers. An overview of the render flow is presented in
Figure 4 for a coarse (Subfigure 4(a)) and a fine (Sub-
figure 4(b)) grid LOD, following the order of the nu-
merical labels. The TIN mesh is the same in both
cases, but the PC grid cells depend on the grid LOD
and thus different cells are rendered for each case.
The first step of the process is to identify the active
NC, CC, and PC cells. Next, the NC cells are ren-
dered using indexed draw calls (step (1) in Figures
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
256
GS
Vertex Indices
i0
i1 i32
i1
i2 ...
NC cells
TIN
PC cells
PC cells indexes
Step 1
Step 2
Step 3
pc4
pc7
(a)
GS
Vertex Indices
i0
i1 i32
i1
i2 ...
NC cells
TIN
PC cells
Step 1
Step 2
Step 3
PC cells indexes
pc8
pc9
pc2
pc6
(b)
Figure 4: HM rendering algorithm steps. (a) Coarse LOD render. (b) Fine LOD render.
Table 1: Size of the test models.
Model Grid cells TIN ∆ TB elems.
Coru
˜
na 998K 1739K 17K
Sil 998K 657K 14K
Pmouros 998K 656K 16K
4(a) and 4(b)), since geometry data is already stored
in the GPU memory. CC cells are then replaced by
the whole TIN mesh (step (2) in the same figures).
This operation is lightweight since TIN meshes are
static, usually cover around 20-30% of the grid exten-
sion, and the geometry data are also stored in the GPU
memory, which makes the rendering very efficient.
Finally, the Geometry Shader which performs the
PC cells adaptive tessellation is loaded and the list of
active PC cells are sent to the GPU, where the actual
tessellation is computed (step (3) in the same figures).
The input of each shader thread is the tessellation data
of the processed PC cell, encoding every data field in
a different vertex attribute. By the time the Geometry
Shader finishes the processing, all the convexification
and corner triangles have been generated and the PC
cell is completely tessellated.
During rendering, each one of the running Geom-
etry Shader threads processes the TB vertices in the
cell sequentially. The associated convexification tri-
angles are reconstructed and emitted by the Geometry
Shader, according to the algorithm presented in Sub-
section 2.2. Vertices belonging to the local convex
hull of the TIN boundary are connected to the grid cell
vertices, by generating additional corner triangles.
In the GPU HM, the sequential tessellation oper-
ations have been reordered and optimized for GPU
execution. Several techniques have been applied, re-
sulting in an implementation of the algorithm with
fewer conditional branch statements, fewer loops
and a reduced number of memory reading opera-
tions. The implementation strategy presented in (B
´
oo
et al., 2007) shows that the decoding and generation
of the incremental convexification triangles, and the
generation of corner triangles are performed in two
stages. We have succeeded in merging these differ-
ent stages together, reducing the overall complexity of
the source code and the number of conditional evalu-
ations of our implementation.
Additional optimization techniques have been also
used when possible, such as loop unrolling and trans-
formation of complex conditional expressions into
arithmetic expressions or several simpler expressions
for faster evaluation. Another relevant performance
improvement derives from the reordering of the TIN
vertices in the vertex buffer. Due to this optimization,
the data of a TB vertex is accessed with the same in-
dex and in the TB list and in the vertex buffer, elimi-
nating the pointer to the geometry data position used
in the original TB list. With this optimization, not
only are data reading operation reduced to almost one
half of the original number, but also many read op-
erations in the same thread could benefit from data
locality and attain much better cache behavior.
4 EXPERIMENTAL RESULTS
The results of our tests are shown in this section. The
software application used for testing has been coded
in C++. GLSL has been used in the shaders, since
OpenGL is the hardware acceleration API. The per-
formance results were collected in a Ubuntu Linux
system with an Intel Core2 Quad 2.6 GHz proces-
sor. Two different Nvidia GeForce graphic cards, an
GTX480 with 1.5GB of video memory and a GTX280
GPU-BASED VISUALIZATION OF HYBRID TERRAIN MODELS
257
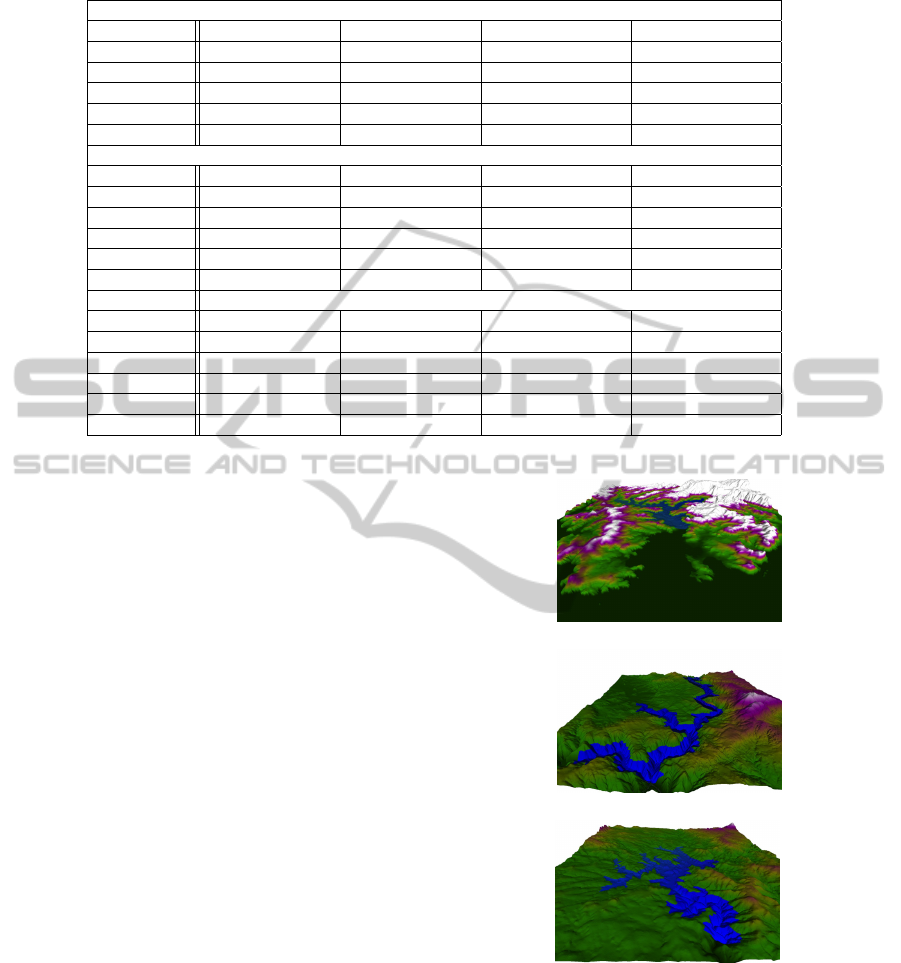
Table 2: Detailed description of the test models composition for each grid LOD.
Coru
˜
na
L0 L1 L2 L3
PC cells 517 (3.36%) 1058 (1.71%) 2142 (0.86%) 4233 (0.43%)
NC cells 14418 (93.77%) 58606 (94.52%) 236079 (94.81%) 949668 (95.16%)
CC cells 441 (2.87%) 2337 (3.76%) 10780 (4.33%) 44100 (4.42%)
Rendered ∆ 1787K 1876K 2231K 3661K
PC cells ∆ 19K (1,06%) 19K (1,01%) 20K (0,89%) 22K (0,60%)
Sil
L0 L1 L2 L3
PC cells 857 (5.57%) 1775 (2.86%) 3510 (1.41%) 7630 (0.76%)
NC cells 13428 (87.33%) 54666 (88.17%) 217694 (87.43%) 904681 (90.65%)
CC cells 1091 (7.10%) 5560 (8.97%) 27797 (11.16%) 85690 (7.10%)
Rendered ∆ 701K 784K 1111K 2489K
PC cells ∆ 17K (2,38%) 17K (2,17%) 19K (1,66%) 23K (0,90%)
Pmouros
L0 L1 L2 L3
PC 821 (5.34%) 1697 (2.74%) 3329(1.34%) 7912 (0.79%)
NC 13640 (88.71%) 55752 (89.92%) 225396 (90.52%) 906434 (90.83%)
CC 915 (5.95%) 4552 (7.34%) 20276 (8.14%) 83655 (8.38%)
Rendered ∆ 704K 804K 1128K 2497K
PC cells ∆ 20K (2,87%) 36K (4,44%) 20K (1,80%) 27K (1,09%)
with 1GB, were used in the tests.
Three sample models, depicted in Figure 5, were
generated for testing purposes from freely available
data in the Spanish GIS database (IDEE) (Infraestruc-
tura de Datos Espaciales de Espa
˜
na (IDEE), 2002):
Coru
˜
na, Sil and Pmouros. Table 1 contains the size
of the sample models in terms of number of cells in
the finest LOD of the grids, number of triangles in the
TIN meshes, and number of vertices in the TB.
In Table 2, the number of PC, CC and NC cells are
shown for each grid LOD from L0 − L3 (where L0
represents the coarsest level) as well as its ratio over
the total number of cells. The last two rows show
the total number of triangles used for rendering the
model and the portion of them corresponding to the
adaptive tessellation of the PC cells. Note that the
Coru
˜
na model presents around twice the number of
rendered triangles, as the TIN mesh is much higher
detailed than the others.
The performance results of the GPU HM method
are shown in Table 3. The table shows the averaged
FPS obtained using the HM algorithm are presented
in comparison to the FPS obtained rendering only the
NC grid cells and the TIN mesh, which represents the
maximum theoretical performance of the system. The
relative performance penalty of our implementation is
shown in parentheses. For each sample model, the
tests results are divided according the active LOD in
the grid (L0 − L3).
As can be seen in the results table, the overhead
introduced by the GPU HM implementation does not
prevent the rendering of large terrain models at inter-
(a)
(b)
(c)
Figure 5: Hybrid models used in the tests with the TIN mesh
highlighted in blue. (a) Coru
˜
na model. (b) Sil hybrid model.
(c) Pmouros hybrid model.
active frame rates. The best performance results are
obtained when the coarser LOD (L0) is selected. For
finer LODs, performance tends to decrease, as the to-
tal number of rendered triangles is much higher. The
cost of the HM algorithm implementation, however,
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
258
Table 3: Performance results obtained with the HM algorithm, measured in FPS, using GTX480 and GTX280 GPUs.
GTX 480
Method L0 L1 L2 L3
Coru
˜
na
NC + TIN 330.90 319.73 283.64 192.91
HM 232.20 (29.83%) 233.62 (26.93%) 213.31 (24.80%) 155.42 (19.43%)
Sil
NC + TIN 758.97 707.51 561.93 293.89
HM 407.83 (46.27%) 409.74 (42.09%) 353.59 (37.08%) 216.00 (26.50%)
Pmouros
NC + TIN 813.42 754.78 591.35 313.56
HM 276.58 (66.00%) 256.32 (66.04%) 348.41 (41.08%) 210.86 (32.75%)
GTX 280
Method L0 L1 L2 L3
Coru
˜
na
NC + TIN 90.30 87.99 79.15 62.02
HM 76.06 (15.77%) 87.61 (0.43%) 78.99 (0.20%) 61.82 (0.32%)
Sil
NC + TIN 306.06 283.13 213.35 125.66
HM 196.54 (35.78%) 194.82 (31.19%) 156.93 (26.44%) 101.49 (19.23%)
Pmouros
NC + TIN 354.43 322.90 233.64 134.77
HM 142.74 (59.73%) 148.63 (53.97%) 159.75 (31.63%) 94.43 (29.93%)
is usually higher for coarser grid LODs, which have
a low degree of parallelism. As shown in Table 2,
the number of PC cells nearly doubles for consecu-
tive finer LODs, while the number of PC tessellation
triangles rises only marginally. Since a new parallel
thread is used for the tessellation of a PC cell, this dif-
ference in the number of PC cells directly affects to
the degree of parallelism in the implementation, and
thus the global performance.
This also explains the noticeable larger perfor-
mance penalty when using the more powerful GTX
480 graphic card (480 cores) compared to the GTX
280 (280 cores). Although the absolute performance
is still much better using the GTX 480, the relative
performance of the HM algorithm is worse, since the
GTX 480 has a larger number of cores and thus fewer
threads are being executed by each core. However,
this effect is only important at very high frame rates
and thus it does not limit the validity of our imple-
mentation. For example, our system is able to render
the largest test model, Coru
˜
na bay, at the maximum
available detail (roughly 3.7 millions of triangles) at
155 FPS using the GTX480 card.
5 CONCLUSIONS
The HM algorithm is an efficient solution for render-
ing hybrid terrain models formed by a base multires-
olution grid mesh and high-resolution TINs. In this
paper we have presented a new implementation of
the method based on Geometry Shaders. Due to this
shader based approach, our implementation is easy to
integrate with any modern rendering pipeline.
This GPU implementation of the HM algorithm is
formed by two phases, like the original algorithm.
The harder computations are performed in the pre-
processing phase, and encoded in simple data struc-
tures. During the rendering, the GPU decodes these
structures and generates the adaptive tessellation at
the same time, joining the component meshes.
The performance of the method, as well as the
quality of the rendered hybrid models has been
demonstrated in our experiments. Our implementa-
tion manages to render models of several millions of
triangles, without geometric discontinuities or over-
lapping, at interactive frame rates. To our knowledge,
no other hybrid terrain rendering algorithm has been
implemented using GPUs.
REFERENCES
B
´
oo, M., Amor, M., and D
¨
ollner, J. (2007). Unified hybrid
terrain representation based on local convexifications.
GeoInformatica, 11(3):331–357.
Infraestructura de Datos Espaciales de Espa
˜
na (IDEE)
(2002). Digital elevation models. http://www.idee.es.
Oosterom, P. v., Zlatanova, S., Penninga, F., and Fendel,
E. (2008). Advances in 3D Geoinformation Systems.
Lecture Notes in Geoinformation and Cartography.
Springer Berlin.
OpenGL.org (2009). OpenGL Texture Buffer Object ext.
Paredes, E. G., B
´
oo, M., Amor, M., Bruguera, J. D., and
D
¨
oellner, J. (To be published). Extended hybrid mesh-
ing algorithm for multiresolution terrain models. Int.
Journal of Geographic Information Science.
Paredes, E. G., Lema, C., Amor, M., and B
´
oo, M. (2009).
Hybrid terrain visualization based on local tessella-
tions. In GRAPP 09: Procs. of the Int. Conf. on Comp.
Graphics Theory and Applications. SciTePress.
Shewchuk, J. (1996). Triangle: Engineering a 2D quality
mesh generator and Delaunay triangulator. Lecture
notes in Computer Science, 1148:203–222.
GPU-BASED VISUALIZATION OF HYBRID TERRAIN MODELS
259
