ARTIFACT-FREE JPEG DECOMPRESSION

WITH TOTAL GENERALIZED VARIATION

Kristian Bredies and Martin Holler

Institute of Mathematics and Scientiﬁc Computing, Karl-Franzens University Graz, Heinrichstraße 36, 8010 Graz, Austria

Keywords:

Artifact-free JPEG Decompression, Total Generalized Variation, Image Reconstruction.

Abstract:

We propose a new model for the improved reconstruction of JPEG (Joint Photographic Experts Group) images.

Given a JPEG compressed image, our method ﬁrst determines the set of possible source images and then

speciﬁcally chooses one of these source images satisfying additional regularity properties. This is realized

by employing the recently introduced Total Generalized Variation (TGV) as regularization term and solving a

constrained minimization problem. In order to obtain an optimal solution numerically, we propose a primal-

dual algorithm. We have developed a parallel implementation of this algorithm for the CPU and the GPU,

using OpenMP and Nvidia’s Cuda, respectively. Finally, experiments have been performed, conﬁrming a

good visual reconstruction quality as well as the suitability for real-time application.

1 INTRODUCTION

This paper presents a novel method for artifact-free

reconstruction of given JPEG compressed images.

Being a lossy compression, a given JPEG compressed

object does not provide exact information about the

original source image, but can be used to deﬁne a

convex set of possible source images. Our method

reconstructs an image in accordance with this given

data and minimal total generalized variation (TGV)

of second order. This recently introduced functional

(Bredies et al., 2010) is well-suited for images as it is

aware of both edges and smooth regions. In particu-

lar, its minimization discourages blocking and ringing

artifacts which are typical for JPEG compressed im-

ages. It not only yields a signiﬁcantly better approxi-

mation of the original image compared to standard de-

compression, but also outperforms, in terms of visual

quality, existing similar variational approaches using

different image models such as, for instance, the total

variation.

The proposed model can be phrased as an inﬁnite

dimensional minimization problem which reads as

min

u∈L

(Ω)

TGV

(u) + I

(u) (1)

where TGV

is the total generalized variation func-

tional of second order and I

a convex indicator

function corresponding to the given image data set

The reason for using the second order TGV func-

tional is that for the moment it provides a good bal-

ance between achieved image quality and computa-

tional complexity. This is true especially since the

improvement in the step from order one to order two,

where order one corresponds to TV regularization, is

visually most noticable (see (Bredies et al., 2010)).

Generalizations to higher orders, however, seem to be

possible and might lead to further improvements.

Among the continuous formulation, we also

present a discretized model and an efﬁcient solu-

tion strategy for the resulting ﬁnite-dimensional mini-

mization problem. Moreover, we address and discuss

computation times of CPU and GPU based parallel

implementations.

Due to the high popularity of the JPEG standard,

the development of improved reconstruction methods

for JPEG compressed images is still an active research

topic. In the following, we shortly address some of

those methods. For a further review of current tech-

niques we refer to (Nosratinia, 2001; Singh et al.,

2007; Shen and Kuo, 1998). A classical approach is to

apply ﬁlters, which only seems effective if space vary-

ing ﬁlters together with a pre-classiﬁcation of image

blocks is used. Another approach is to use algorithms

based on projections onto convex sets (POCs), see for

example (Kartalov et al., 2007; Weerasinghe et al.,

2002; Zou and Yan, 2005), where one deﬁnes several

convex sets according to data ﬁdelity and regulariza-

tion models. Typical difﬁculties of such methods are

Bredies K. and Holler M..

ARTIFACT-FREE JPEG DECOMPRESSION WITH TOTAL GENERALIZED VARIATION.

DOI: 10.5220/0003824500120021

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 12-21

ISBN: 978-989-8565-03-7

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

the concrete implementation of the projections and its

slow convergence.

Our approach, among others, can be classiﬁed as

a constrained optimization method, where the con-

straints are deﬁned using the available compressed

JPEG data. One advantage of this method is that, in

contrast to most ﬁlter based methods, we do not mod-

ify the image, but choose a different reconstruction

in strict accordance to the set of possible source im-

ages. Since data ﬁdelity is numerically realized by

a projection in each iteration, we can ensure that at

any iteration, the reconstructed image is at least as

plausible as the standard JPEG reconstruction. Let us

stress, however, that the idea of reconstructing JPEG

images by minimizing a regularization functional un-

der constraints given by the compressed data is not

new. In (Bredies and Holler, 2011; Alter et al., 2005;

Zhong, 1997) this was done using the well known

total variation (TV) as regularization functional. In

contrast to quadratic regularization terms, this func-

tional is known to smooth the image while still pre-

serving jump discontinuities such as sharp edges. But

still, total variation regularized images typically suffer

from the so called staircasing effect (Nikolova, 2000;

Caselles et al., 2007; Ring, 2000), which limits the

application of this method for realistic images.

The total generalized variation functional (TGV),

introduced in (Bredies et al., 2010), does not suffer

from this defect. As the name suggests, it can be

seen as a generalization of the total variation func-

tional: The functional may be deﬁned for arbitrary

order k ∈N, where in the case k = 1, it coincides with

the total variation functional up to a constant. We will

use the total generalized variation functional of order

2 as regularization term. As we will see, the appli-

cation of this functional has the same advantages as

the total variation functional in terms of edge preserv-

ing, with the staircasing effect being absent. Never-

theless, evaluation of the TGV functional of second

order yields a minimization problem itself and non-

differentiability of both the TGV functional as well

as the convex indicator function used for data ﬁdelity

make the numerical solution of our constrained opti-

mization problem demanding.

The outline of the paper is as follows: In Section

2 we shortly explain the JPEG compression standard

and introduce the TGV functional, in Section 3 we de-

ﬁne the continuous and the discrete model and present

a numerical solution strategy, in Section 4 we present

experiments including computation times of CPU and

GPU based implementations and in Section 5 we give

a conclusion.

DCT

Quantization

Lossless

compression

8x8 blocks

Source

Image data

Compressed

Image data

Quantization

table

Figure 1: Schematic overview of the JPEG compression

procedure, taken from (Bredies and Holler, 2011).

2 THEORETICAL BACKGROUND

2.1 The JPEG Standard

At ﬁrst we give a short overview of the JPEG standard

which is partly following the presentation in (Bredies

and Holler, 2011). For a more detailed explanation

we refer to (Wallace, 1991). The process of JPEG

compression is lossy, which means that most of the

compression is obtained by loss of data. As a con-

sequence, the original image cannot be restored com-

pletely from the compressed object.

Let us for the moment only consider JPEG com-

pression for grayscale images. Figure 1 illustrates the

main steps of this process. At ﬁrst, the image un-

dergoes a blockwise discrete cosine transformation

resulting in an equivalent representation of the im-

ages as the linear combination of different frequen-

cies. This makes it easier to identify data with less

importance to visual image quality such as high fre-

quency variations. Next the image is quantized by

pointwise division of each 8 ×8 block by a uniform

quantization matrix. The quantized values are then

rounded to integer, which is where the loss of data

takes place, and after that these integer values are fur-

ther compressed by lossless compression. The result-

ing data, together with the quantization matrix, is then

stored in the JPEG object.

Decoding Dequantization

Inverse

DCT

Source

Image data

Restored

Image

Quantization

table

Figure 2: Schematic overview of the standard JPEG decom-

pression procedure, taken from (Bredies and Holler, 2011).

The standard JPEG decompression, as shown in

Figure 2, simply reverses this process without taking

into account incompleteness of the data, i.e., that the

compressed object delivers not a uniquely determined

ARTIFACT-FREE JPEG DECOMPRESSION WITH TOTAL GENERALIZED VARIATION

Figure 3: JPEG image with typical blocking and ringing

artifacts.

image, but a convex set of possible source images. In-

stead it just assumes the rounded integer value to be

the true quantized DCT coefﬁcient which leads to the

well known JPEG artifacts as can be seen, for exam-

ple, in Figure 3.

In the case of color images, typically a subsam-

pling of color components is performed as part of

JPEG compression. For that, color images are pro-

cessed in the YCbCr color space, i.e., the images are

given as u = (y,cb,cr), where y is the luminance com-

ponent and cb,cr are chroma components. Subsam-

pling is then applied to the chroma components cb

and cr, which reﬂects the fact that the human eye

is less sensitive to color variations than to bright-

ness variations. The resulting three image compo-

nents, which now differ in resolution, then undergo

the same process as grayscale images (see Figure

4). Again, the standard JPEG decompression simply

reverts this process, now by applying an additional

chroma-upsampling as last step.

An integral part of the model we propose is taking

the set of all possible source images associated with

a given JPEG object as a constraint. This set can be

mathematically described as follows. With the integer

coefﬁcient data (d

i, j

), where the range of i, j depends

on the resolution of the color component c ∈{0, 1,2},

and the quantization matrix (Q

i, j

)

0≤i, j<8

, both pro-

vided by the compressed JPEG object, the set of num-

bers which yield d

i, j

in the quantization and rounding

step is given by the interval

i, j



i, j

−

),Q

i, j

)



. (2)

Note that for this notation we extend the quantization

matrices up to the image dimensions simply by re-

peating the 8 ×8 coefﬁcients. Having this, the coefﬁ-

cient data set D can be deﬁned as

D =



i, j

)|z

i, j

∈ J

i, j

for all c,i, j



(3)

and the set of possible source images of the compres-

sion process as



u = (u

i, j

)|ASu ∈D



(4)

where A is a color-component-wise blockwise DCT

operator and S is a subsampling operator (see Subsec-

tion 3.2 for the deﬁnition of A and S).

2.2 The TGV Functional

Another building block of the model is the total gen-

eralized variation functional (TGV) as proposed in

(Bredies et al., 2010), in particular of second order.

We give here a short deﬁnition and sum up some im-

portant results, for details and proofs however, we

refer to (Bredies et al., 2010; Bredies and Valko-

nen, 2011). The pre-dual formulation of second-order

TGV is given by

TGV

(u) = sup

(

Ω

udiv

v dx



v ∈C

(Ω,S

2×2

kvk

∞

≤ α

,kdivvk

∞

≤ α

)

, (5)

where α = (α

,α

) ∈ R

, u ∈ L

(Ω) and S

2×2

is the

space of symmetric 2 by 2 matrices. Given a function

u ∈ L

(Ω), the second-order TGV functional takes

into account, as the test functions have the form div

the generalized derivative of u up to order 2. Its kernel

is the set of polynomials with degree less than 2. Eval-

uation of TGV

can be also interpreted as an optimal

balancing of the ﬁrst and second generalized deriva-

tive of u among themselves. This becomes obvious,

considering an equivalent representation of TGV

TGV

(u) = inf

v∈BD(Ω,R

)

k∇u −vk

+ α

kE (v)k

(6)

Here, E (v) denotes the symmetrized derivative of the

vector ﬁeld v and BD(Ω) the space of vector ﬁelds

of bounded deformation. As one can also see in (6),

the ratio between the parameters α

and α

weights

the balancing between the ﬁrst and second derivative

of u and will later also inﬂuence possible solutions of

TGV

regularized optimization problems. The TGV

functional possesses several properties which support

its usage as regularization term, such as convexity and

lower semi-continuity with respect to L

convergence.

It also satisﬁes a Poincar

e-Wirtinger type inequality

which can be used to obtain coercivitiy of the objec-

tive functional.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

YCbCr

246

100

230

226

165

246

100

230

226

165

230 226

124

Grayscale-JPEG

Compressed image data

8 6 15 2 7 4 3 1

Figure 4: Chroma subsampling during JPEG compression.

3 THE METHOD

This section is devoted to present the TGV-based

JPEG reconstruction method. Let us at ﬁrst state the

associated minimization problem in an inﬁnite dimen-

sional setting. Note that we abuse notation by using

the same symbols for the continuous setting as for the

discrete one.

3.1 The Continuous Setting

For convenience we only consider grayscale images

for the continuous setting. Hence, our images are rep-

resented by real valued functions u ∈ L

(Ω) with Ω a

bounded Lipschitz domain, typically a rectangle. Us-

ing the deﬁnition of the TGV functional given in (5)

we can formulate the inﬁnite dimensional minimiza-

tion problem as follows:

min

u∈L

(Ω)

TGV

(u) + I

(u) (7)

where

(u) =

(

0 if u ∈U

∞ else.

The data set U

can be deﬁned as

= {u ∈ L

(Ω)|Au ∈ D}

where A is a basis transformation operator related to

a general orthonormal basis (a

)

n≥0

of L

(Ω). The

coefﬁcient data set D ⊂`

reﬂects interval restrictions

on the coefﬁcients:

D = {z ∈ `

∈ J

∀i ∈ N

}

where J

⊂ R is a non-empty, closed (not necessarily

bounded) interval for any i ∈N

. Note that this model

allows arbitrary orthonormal bases (a

)

n≥0

of L

(Ω)

and constraints on inﬁnitely many coefﬁcients. How-

ever, for JPEG decompression, one usually chooses

an inﬁnite block-cosine orthonormal basis, and lets

only the J

associated with the ﬁrst 8 ×8 blockwise

coefﬁcients be bounded and J

= R for the remaining

i, see (Bredies and Holler, 2011) for details.

Under assumptions which are satisﬁed in the ap-

plication of this model to JPEG decompression, we

can show existence of a solution to (7). More gen-

erally, if we assume that U

has non-empty interior

and that J

are bounded for certain n

existence of a solution can be guaranteed.

3.2 The Discrete Model

Based on the equivalent formulation of the TGV func-

tional in (6) and the data set U

as in (4) we will now

formulate our discrete model.

For k,l ∈ N, we set the space of discrete color im-

ages U = R

8k×8l×3

and further V = U

and W = U

The dimension 8k×8l ×3 results from the three color

components and reﬂects the fact that any JPEG image

is processed with its horizontal and vertical number

of pixels being multiples of 8.

Now for u ∈U, a discrete vector-input version of

the TGV

functional can be deﬁned as

TGV

(u) = inf

v∈V

k∇(u) −vk

+ α

kE (v)k

, (8)

ARTIFACT-FREE JPEG DECOMPRESSION WITH TOTAL GENERALIZED VARIATION

where ∇ : U → V denotes a discrete, color-

component-wise gradient operator using forward dif-

ferences and E : V → W denotes a discrete, color-

component-wise symmetric gradient operator using

backward differences, i.e., E (v) =

(J(v) + J(v)

)

with J(v) a discrete color-component-wise Jacobian

of v. Note that in E (v), the off-diagonal entries

need to be stored only once, thus E(v) ∈ U

. For

v = (v

i, j

)

0≤i, j<8k

with v

i, j

∈ R

3×2

the norm on V is

deﬁned as

kvk

∑

i, j

with |·| the Frobenius norm on R

3×2

. The norm k·k

is deﬁned similarly.

In order to avoid extensive indexing, we will now

give just a local, component-wise deﬁnition of the op-

erators S and A, necessary to describe the data set U

The subsampling operator S depends on the foregoing

chroma subsampling process, but typically is deﬁned

on disjoint 2 ×2 blocks of each chroma component,

denoted by (z

i, j

)

0≤i≤1

, as

Sz =

∑

m,n=0

m,n

reducing the resolution of the chroma components by

the factor 4. Since the resolution of the brightness

component is not reduced, S is the identity for this

component. The discrete cosine transformation op-

erator is deﬁned, for each color component, on each

disjoint 8 ×8 block (z

i, j

)

0≤i, j≤7

, as

(Az)

p,q

= C

∑

n,m=0

n,m

cos



π(2n + 1)p



cos



π(2m + 1)q



for 0 ≤ p, q ≤ 7 and

(

√

if s = 0,

if 1 ≤ s ≤ 7.

With the operators S and A, the set U

can now be

deﬁned as already done before in (4) by

= {u ∈U |ASu ∈ D},

where the coefﬁcient data set D is obtained from the

compressed JPEG object as in (3).

With these prerequisites, the ﬁnite dimensional

optimization problem for artifact-free JPEG decom-

pression reads as

min

u∈U

TGV

(u) + I

(u), (9)

where again

(u) =

(

0 if u ∈U

∞ else.

Using the boundedness of the data intervals J

i, j

deﬁned in (2) it can be shown that there exists a solu-

tion to (9) and that this problem is equivalent to

min

(u,v)∈U ×V

F(K(u, v)) + I

(u), (10)

where K : U ×V →V ×W,

K =



∇ −1

0 E



and F : V ×W → R,

F(v,w) = α

kvk

+ α

kwk

This formulation will now be the basis for the numer-

ical approach.

3.3 A Primal-dual Algorithm

We numerically solve our minimization problem us-

ing a primal-dual algorithm presented in (Chambolle

and Pock, 2011), for which convergence can be en-

sured. This algorithm is well-suited for this problem

because, as we will see, all necessary steps during one

iteration reduce to simple arithmetic operations and

the evaluation of a forward and inverse block-cosine

transformation, for which highly optimized code al-

ready exists. This makes the algorithm fast and also

easy to implement on the GPU.

As ﬁrst step we note that (10) is equivalent to the

following saddle-point problem:

min

x∈X

max

y∈Y

((y,Kx)

Y,Y

−F

∗

(y) + I

(x)) (11)

where X = U ×V , Y = V ×W , (·,·) is the scalar

product on Y and F

∗

is the convex conjugate of F.

The primal-dual strategy for ﬁnding saddle points pre-

sented in (Chambolle and Pock, 2011) amounts to

performing the abstract iteration shown in Algorithm

1. Note that ∂F

∗

and ∂I

refers to the subdifferen-

tial of F

∗

and I

, respectively, and the operator K

∗

denotes the adjoint of K and is given by

∗



−div 0

−1 −div



with div = −∇

∗

and div

= −E

∗

denoting discrete

divergence operators.

Using standard arguments from convex analysis,

it can be shown that the resolvent-type operators (I +

σ ∂ F

∗

)

−1

and (I +τ ∂ I

)

−1

take the following form:

(I + σ∂F

∗

)

−1

(v, w) =



proj

(v),proj

(w)



VISAPP 2012 - International Conference on Computer Vision Theory and Applications

where

proj

(v) =

max(1,

kvk

∞

)

proj

(w) =

max(1,

kwk

∞

)

and

(I + τ ∂I

)

−1

(u,v) =



u + S

−1



proj

(Su) −Su



where

proj

(u) = A

∗

with

i, j











i, j

if (Au)

i, j

∈ J

i, j

= [l

i, j

]

i, j

if (Au)

i, j

> r

i, j

if (Au)

i, j

< l

i, j

∗

= A

−1

the adjoint of A and S

−1

denoting the up-

sampling operator associated with S, given locally by

replication of z ∈ R, i.e.,

−1

z =



z z



Having this, we can now give the concrete imple-

mentation of the primal-dual algorithm for JPEG de-

compression in Algorithm 2. Note that the step-size

restriction στ ≤

results from the estimate kKk

12. As one can see, all steps of Algorithm 2 can

be evaluated by simple, mostly pixel-wise operations

making each iteration step fast.

4 NUMERICAL EXPERIMENTS

We implemented and tested the proposed TGV-based

JPEG decompression method. First of all, we have

compared the standard JPEG decompression with our

method for three images possessing different charac-

teristics. The outcome can bee seen in Figure 5, where

also the image dimensions and the memory require-

ment of the JPEG compressed image is given in bits

Algorithm 1: Abstract primal-dual algorithm.

• Initialization: Choose τ,σ > 0 such that

kKk

τσ < 1, (x

) ∈ X ×Y and set x

= x

• Iterations (n ≥0): Update x

as follows:











n+1

= (I + σ ∂ F

∗

)

−1

+ σKx

)

n+1

= (I + τ ∂I

)

−1

−τK

∗

n+1

)

n+1

= 2x

n+1

−x

per pixel (bpp). As one can see, our method performs

well in reducing the typical JPEG artifacts and still

preserves sharp edges.

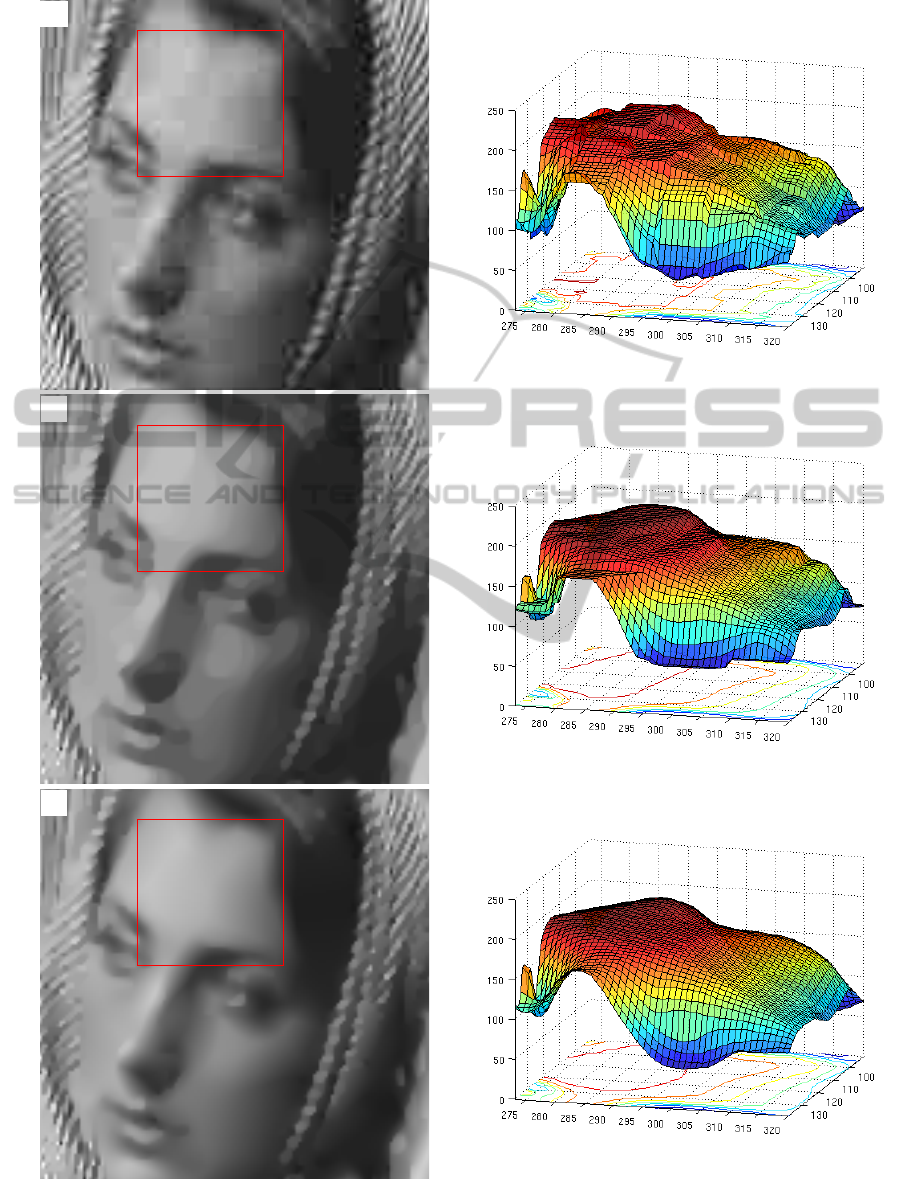
Figure 6 then allows to compare our results with

the reconstruction using TV instead of TGV as reg-

ularization functional as proposed in (Bredies and

Holler, 2011). As one can see, in particular in the sur-

face plots, the TV-based method also maintains sharp

edges. However, it leads to a staircasing effect in re-

gions that should be smooth. In contrast to that, the

TGV-based method yields a more natural and visually

more appealing reconstruction in such regions.

Figure 7 serves as an example of an image con-

taining texture. It can be seen that our method pre-

serves ﬁne details and does not lead to additional

smoothing of textured regions.

We also developed a parallel implementation of

the method for multi-core CPUs and GPUs, us-

ing OpenMP (OpenMP Architecture Review Board,

2011) and Nvidia’s Cuda (NVIDIA, 2008), respec-

tively. For the GPU implementation we partly used

kernel functions adapted to the compute capability of

the device. The blockwise DCT was performed on

the CPU and the GPU using FFTW (Frigo and John-

son, 2005) and a block-DCT kernel provided by the

Cuda SDK, respectively. Computation times of those

implementations for multiple image sizes are given in

Table 1. As one can see, especially the GPU imple-

mentation yields a high acceleration and makes the

method suitable for real-time applications. The given

Algorithm 2: Scheme of implementation.

1: function TGV-JPEG(J

comp

)

2: (d,Q) ← Decoding of JPEG-Object J

comp

3: d ← d ·Q

4: u ←S

−1

∗

(d))

5: v ←0,u ←u,v ←0, p ←0,q ←0

6: choose σ,τ > 0 such that στ ≤1/12

7: repeat

8: p ← proj

(p + σ(∇u −v))

9: q ← proj

(q + σ(E (v))

10: u

← u + τ(div p)

11: v

← v + τ(p + div

12: u

← u

+ S

−1

(proj

(Su

) −Su

)

13: u ← (2u

−u), v ← (2v

−v)

14: u ← u

, v ← v

15: until Stopping criterion fulﬁlled

16: return u

17: end function

ARTIFACT-FREE JPEG DECOMPRESSION WITH TOTAL GENERALIZED VARIATION

A B

C D

E F

Figure 5: On the left: Standard decompression, on the right: TGV-based reconstruction after 1000 iterations. A-B: SciTePress

image at 0.5 bpp (256 ×256 pixels). C-D: Peppers image at 0.15 bpp (512 ×512 pixels). E-F: Parrot image at 0.3 bpp

(256 ×256 pixels).

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

Figure 6: Close-up of Barbara image at 0.4 bpp at 1000 iterations. The marked region on the left is plotted as surface on the

right. A: Standard decompression. B: TV-based reconstruction. C: TGV-based reconstruction.

ARTIFACT-FREE JPEG DECOMPRESSION WITH TOTAL GENERALIZED VARIATION

Table 1: Computation times in seconds to perform 1000 iterations for different devices and image sizes. CPU: AMD Phenom

9950. GPUs: Nvidia Quadro FX 3700 (compute capability 1.1), Nvidia GTX 280 (compute capability 1.3), Nvidia GTX 580

(compute capability 2.0). Note that on the Quadro FX 3700 and GTX 280, not enough memory was available to perform the

algorithm for the 3200 ×2400 pixel image.

Device 512 ×512 1600 ×1200 3200 ×2400

CPU Single-core 53.22 672.51 1613.44

CPU Quad-core 28.32 263.70 812.18

GPU Quadro FX 3700 4.92 35.52 -

GPU Nvidia GTX 280 2.2 10.22 -

GPU Nvidia GTX 580 1.2 6.6 25.70

Figure 7: From left to right: Uncompressed image at 24 bpp (256 ×256 pixels), standard decompression of JPEG com-

pressed image at 1.06 bpp, TGV-based reconstruction of the same JPEG compressed image after 1000 iterations. Image by

(Dawgbyte77, 2008), licensed under CC-BY-2.0 (http://creativecommons.org/licenses/by/2.0/).

computation times correspond to the computation of

1000 iterations, which is in most cases more than

enough for a reconstruction visually almost indistin-

guishable from one obtained as optimal solution satis-

fying a suitable stopping criterion. Since the decrease

of the TGV-value of the image is typically very high

especially during the ﬁrst iterations of the algorithm,

and since a ﬁt-to-data can be ensured for any iteration

step image, one could use the image obtained after

only a few number of iterations as intermediate re-

construction and then iteratively update the solution.

5 SUMMARY AND

CONCLUSIONS

We proposed a novel method for the improved recon-

struction of given JPEG compressed images, in partic-

ular, color images. The reconstruction is performed

by solving a non-smooth constrained optimization

problem where exact data ﬁdelity is achieved by the

usage of a convex indicator functional. The main nov-

elty, however, lies in the utilization of TGV of sec-

ond order as a regularization term which intrinsically

prefers natural-looking images, as it has been con-

ﬁrmed in Section 4. This was shown to be true not

only with respect to the standard reconstruction, but

also with respect to already-known TV-based recon-

struction methods.

Moreover, a parallel implementation for multi-

core CPUs and GPUs showed that this reconstruction

process can be realized sufﬁciently fast in order to

make the method also applicable in practice.

Motivated by these promising results, the focus of

further research will be the development of a theory

for a more general model using the TGV functional

of arbitrary order.

ACKNOWLEDGEMENTS

Support by the Austrian Science Fund FWF under

grant SFB F032 (“Mathematical Optimization and

Applications in Biomedical Sciences”) is gratefully

acknowledged.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

REFERENCES

Alter, F., Durand, S., and Froment, J. (2005). Adapted to-

tal variation for artifact free decompression of JPEG

images. Journal of Mathematical Imaging and Vision,

23:199–211.

Bredies, K. and Holler, M. (2011). A total-variation-

based JPEG decompression model. Submitted

for publication. Preprint available at http://math.uni-

graz.at/mobis/publications.html.

Bredies, K., Kunisch, K., and Pock, T. (2010). Total gener-

alized variation. SIAM Journal on Imaging Sciences,

3(3):492–526.

Bredies, K. and Valkonen, T. (2011). Inverse problems with

second-order total generalized variation constraints.

In Proceedings of SampTA.

Caselles, V., Chambolle, A., and Novaga, M. (2007). The

discontinuity set of solutions of the TV denoising

problem and some extensions. Multiscale Model.

Simul., 6:879–894.

Chambolle, A. and Pock, T. (2011). A ﬁrst-order primal-

dual algorithm for convex problems with applications

to imaging. Journal of Mathematical Imaging and Vi-

sion, 40:120–145.

Dawgbyte77 (2008). http://www.ﬂickr.com/photos/dawg-

byte77/3052164481/.

Frigo, M. and Johnson, S. G. (2005). The design and im-

plementation of FFTW3. Proceedings of the IEEE,

93(2):216–231. Special issue on “Program Genera-

tion, Optimization, and Platform Adaptation”.

Kartalov, T., Ivanovski, Z. A., Panovski, L., and Karam,

L. J. (2007). An adaptive POCS algorithm for com-

pression artifacts removal. In 9th International Sym-

posium on Signal Processing and Its Applications,

pages 1–4.

Nikolova, M. (2000). Local strong homogeneity of a regu-

larized estimator. SIAM J. Appl. Math., 61:633–658.

Nosratinia, A. (2001). Enhancement of JPEG-compressed

images by re-application of JPEG. The Journal of

VLSI Signal Processing, 27:69–79.

NVIDIA (2008). NVIDIA CUDA programming guide 2.0.

NVIDIA Cooperation.

OpenMP Architecture Review Board (2011). Openmp

application program interface, version 3.1.

http://www.openmp.org.

Ring, W. (2000). Structural properties of solutions to to-

tal variation regularization problems. M2AN Math.

Model. Numer. Anal., 34:799–810.

Shen, M.-Y. and Kuo, C.-C. J. (1998). Review of postpro-

cessing techniques for compression artifact removal.

Journal of Visual Communication and Image Repre-

sentation, 9(1):2–14.

Singh, S., Kumar, V., and Verma, H. K. (2007). Reduc-

tion of blocking artifacts in JPEG compressed images.

Digital Signal Processing, 17(1):225–243.

Wallace, G. K. (1991). The JPEG still picture compression

standard. Commun. ACM, 34(4):30–44.

Weerasinghe, C., Liew, A. W.-C., and Yan, H. (2002). Arti-

fact reduction in compressed images based on region

homogeneity constraints using the projection onto

convex sets algorithm. IEEE Transactions on Circuits

and Systems for Video Technology, 12(10):891–897.

Zhong, S. (1997). Image coding with optimal reconstruc-

tion. In International Conference on Image Process-

ing, volume 1, pages 161–164.

Zou, J. J. and Yan, H. (2005). A deblocking method for

BDCT compressed images based on adaptive projec-

tions. IEEE Transactions on Circuits and Systems for

Video Technology, 15(3):430–435.

ARTIFACT-FREE JPEG DECOMPRESSION WITH TOTAL GENERALIZED VARIATION