DETECTION AND LOCALISATION OF STATIONARY OBJECTS
WITH A PAIR OF PTZ CAMERAS
Constant Guillot
1
, Quoc-Cuong Pham
1
, Patrick Sayd
1
, Christophe Tilmant
2
and Jean-Marc Lavest
2
1
CEA LIST, Vision and Content Engineering Laboratory, BP 94, Gif-sur-Yvette, F-91191 France
2
LASMEA UMR 6602, PRES Clermont Universit
´
e/CNRS, 63177 Aubi
`
ere cedex, France
Keywords:
Stationary Object, PTZ Camera, Multiview Matching.
Abstract:
We propose a novel approach for detecting and localising stationary objects using a pair of PTZ cameras
monitoring a wide scene. First we propose a stationary object detection and labelling algorithm. It relies
on the re-identification of foreground blocks of the image and an MRF framework to detect and separate the
stationary objects of the scene. Second we propose a geometric approach for robustly matching the detected
silhouettes of stationary objects from a pair of PTZ cameras. Our system is tested on challenging sequences
which prove its robustness to occlusions even in an unknown non planar 3D scene.
1 INTRODUCTION
With the increasing number of CCTV cameras in pub-
lic places a lot of effort has been done to build auto-
mated systems capable of detecting events of interest.
These systems make possible the effective surveil-
lance of areas by a limited number of operators and
therefore allow the use of an active video-surveillance
at a real scale.
Detection of stationary objects is a preliminary
task required by many topical applications. The main
difficulties of this task, which is very often addressed
using background subtraction techniques, are the ro-
bustness to changes in illumination and to occlusions.
In this paper, we propose a novel system to detect
stationary objects with a pair of PTZ cameras moni-
toring a wide area. Each camera independently mon-
itors the scene by going through a predefined set of
positions (pan, tilt, zoom) in order to cover the area at
an adapted resolution. Each of these positions, which
we will refer to as a view, can be seen as an indepen-
dent stationary camera with a very low frame rate.
The contribution of this paper is twofold. First,
stationary objects are detected and labelled indepen-
dently in each view. The labelling phase allows, in
some cases, the distinction of several objects which
are part of a single blob. This is done through the re-
identification of the foreground through time and the
minimisation of an energy under an MRF framework.
The second contribution consists in matching the sil-
houettes from one camera to the other. The main diffi-
culty stands in dealing with an arbitrary 3D scene (not
necessary planar) and with the large baseline between
the two cameras.
2 RELATED WORK
In the past years many approaches were proposed to
detect stationary objects, the main difficulty being ro-
bustness to occlusions. In (Mathew et al., 2005) the
authors use a mixture of Gaussians to model the back-
ground and the foreground. Stationary objects are
detected by analysing the transitions of the state of
Gaussians from foreground to background. In (Guler
et al., 2007) the authors propose to track moving ob-
jects in the scene and define for each object an en-
durance probability which is incremented when the
object does not fit the background model. In (Porikli
et al., 2008) the authors use a short term and a long
term background model. They assume that station-
ary objects will enter the short term model, and state
that an object is static if it is in the short term model
but not in the long term model. Then, they update
an evidence map image which counts the number of
times a pixel has been classified as stationary. In
(Liao et al., 2008) the authors use foreground mask
sampling to detect stationary objects. They use 6
foreground masks equally distributed through the last
30 seconds and compute the logical “and” of these
masks. Although this method has been proved (Bay-
591
Guillot C., Pham Q., Sayd P., Tilmant C. and Lavest J..
DETECTION AND LOCALISATION OF STATIONARY OBJECTS WITH A PAIR OF PTZ CAMERAS.
DOI: 10.5220/0003827205910596
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 591-596
ISBN: 978-989-8565-03-7
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

ona et al., 2009) to be one of the best approaches, it
raises many false alarms. This work has however been
extended recently in (Bayona et al., 2010). They pre-
vent false alarms caused by moving objects by build-
ing a mask of moving regions.
Effort has been done to try to achieve robust-
ness to occlusions. However, methods based on sub-
sampling, which were proved to perform the best
(Bayona et al., 2009), rely on the on logical opera-
tions which cannot guarantee that the same object is
observed.
In the past years, multi-camera object localisation
has already been studied. In (Beynon et al., 2003) the
authors make a ground plane assumption and can thus
easily retrieve the world coordinates. A cost func-
tion based on colour, blob area and position is built to
measure the similarity of 2D observations to already
observed 3D world objects. They use a linear assign-
ment problem algorithm to perform an optimal asso-
ciation between observations and tracked objects. In
(Miezianko and Pokrajac, 2008) the authors also as-
sume that the 3D scene is planar. Once they have lo-
cated an object in a camera, it is projected onto the 2D
plane using a homography. The location of objects
are the local maxima of overlap in the orthoimage. In
(Utasi and Csaba, 2010) the authors define an energy
function based on geometric features depending on
the position and height of objects and which is max-
imal for the real configuration. The optimal configu-
ration is found using multiple death and birth dynam-
ics, an iterative stochastic optimisation process. In
(Fleuret et al., 2008) the authors discretise the ground
plane into a grid. A rectangle modelling a human sil-
houette is projected on cameras from each position
on the grid. This serves as an evidence of the occu-
pancy of the ground by a person. In (Khan and Shah,
2009) the authors introduce a planar homographic oc-
cupancy constraint which fuses foreground informa-
tion from multiple cameras. This constraint brings
robustness to occlusion and allows the localisation of
people on a reference plane.
Among these methods some assume that the 3D
world is planar through the use of homographies,
other because they have to reduce the search space
for their optimisation process. We will propose a di-
rect matching method which enables the computation
of 3D positions and heights of stationary objects.
3 OBJECT DETECTION
Our stationary object detection algorithm can be di-
vided into three main steps. First a background sub-
traction stage generates an image containing the age
of the re-identified foreground. Then this informa-
tion is used to generate a segmentation of the visible
stationary objects. Finally one binary mask for each
stationary object is updated.
3.1 Background Subtraction
We use the background subtraction algorithm from
(Guillot et al., 2010) and extend it by building also
a foreground model. The original image is tiled as
a regular square grid of 8 × 8 blocks on which over-
lapping descriptors are computed. The background
subtraction therefore generates an image whose pixels
can be assimilated to the blocks of the original image.
To this aim, a descriptor is computed at each
block. If it doesn’t match the background model then
it is checked against the foreground model. If a match
is found in the foreground model then it is updated,
otherwise a new foreground component is created and
its time of creation is recorded. The foreground model
at a specific block is emptied when background is ob-
served. Thus, the output of the background subtrac-
tion stage is an image whose pixels contain 0 when
background is observed, or the age of the foreground
descriptor.
3.2 What We Want to Segment
Segmenting unknown stationary objects is a very dif-
ficult problem which we will not try to address in the
general case. For instance, if two objects appear at
the same time and are detected as a single blob in the
image, we do not try to separate them. What we want
to do is to give different labels to objects appearing
at different times while giving a single label to an ob-
ject appearing under partial occlusion (eg: a man par-
tially occludes a baggage then leaves). This is not an
easy task since at a block level it is impossible to state
whether we are observing an object or an occluder.
To this aim we construct in 3.3 an energy func-
tion under the following assumption. Blocks should
be grouped under a same label l when l is a compati-
ble label for all these blocks.
3.3 Segmentation
Markov Random Fields are widely used in image seg-
mentation when the problem can be written as the
minimisation of an energy function. Let G = (V, E)
be a graph representing an image. Each vertex v ∈ V
corresponds to a pixel of the image, and each edge
e ∈ E ⊆ V ×V corresponds to a neighbourhood rela-
tion. Let L be a set of labels.Each labelling x ∈ L
|V |
is assigned an energy, which we try to minimise. The
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
592

considered energy function are of the form E : L
|V |
→
R and satisfy:
E(x) =
∑
i∈V
D
i
(x
i
) +
∑
(i, j)∈E
V
i j
(x
i
, x
j
) (1)
where D
i
(x
i
), called the data or unary term, repre-
sents the cost of assigning label x
i
to vertex i ∈ V , and
V
i, j
(x
i
, x
j
) called smoothing or binary term represents
the cost of assigning different labels to neighbouring
vertices.
To minimise the energy function we use the algo-
rithm proposed in (Alahari et al., 2008), which guar-
antees a good and fast approximation of the optimum
labelling.
We now define our energy function E constructed
in such a way that ˆx = argmin
x
E(x) is a labelling of the
image corresponding to the visible stationary objects.
Let L = {l
BG
, l
1
, . . . , l
n
} be our set of labels, with
l
BG
being the label for both background and non sta-
tionary objects, and l
1
, . . . , l
n
the labels of n distinct
stationary objects.
D
i
(l
BG
) = 0 (2)
Equation 2 states that the cost of the non stationary
label is equal to 0. In other terms this label is chosen
by default, unless the stationary object conditions are
met.
D
i
(x
i
6= l
BG
) = C − age
i
+ pTemporal
i
(x
i
)
+pIncompatibility
i
(x
i
) (3)
with C > 0 being the lapse of time necessary to
consider that an object is stationary, and age
i
the
age of the foreground block i. The pTemporal and
pIncompatibility penalties are defined in equations 4
and 5:
pTemporal
i
(x
i
) = max(t
x
i
−t
i
−C, 0) (4)
where t
x
i
is the time of the first assignment of label
x
i
to a block, and t
i
is the time of first appearance of
the foreground block i
pIncompatibility
i
(x
i
) = max(t
i,
/
0
−t
x
i
+C, 0) (5)
where t
i,
/
0
is the time background was last seen at
block i.
From equation 3 we can see that D
i
(x
i
6= l
BG
) <
D
i
(l
BG
) only if age
i
> C. In other terms assigning a
stationary object label to a block costs less than the
assignment of the l
BG
label only if this block is old
enough. A priori any label can be assigned to a block
considered as stationary, however we make two as-
sumptions (equations 4 and 5) which allow us to ob-
tain the desired segmentation.
The pTemporal
i
penalty (equation 4) is positive
for a label x
i
at a block i when its time of assign-
ment is posterior of more than C to the time of the
first observation of the foreground block i. Labels
whose time of creation is after t
i
+C are therefore pe-
nalised. However, labels which were assigned before
time t
i
+C are not penalised because we have no ev-
idence that these labels are incompatible with block
i.
The pIncompatibility
i
penalty (equation 5) is pos-
itive for a label x
i
at a block i if label x
i
was already
assigned to another block while background was ob-
served at block i.
The smoothing term is defined in equation 6 as
follows:
V
i j
(x
i
, x
j
) =
(
λ
1
+ λ
2
exp
−|age
i
−age
j
|
2
if x
i
6= x
j
0 if x
i
= x
j
(6)
with λ
1
and λ
2
> 0. The role of λ
1
is to pe-
nalise the labelling of two neighbouring blocks by
two different labels. The role of the exponential
term, weighted by λ
2
, is to penalise the assignment
of different labels to neighbouring foreground blocks
which have a similar age.
3.4 Masks Update
The use of the MRF to find a labelling with our en-
ergy function E gives us a segmentation of the visi-
ble part of stationary objects. In order to keep track
of the occluded stationary objects we maintain up-
dated one binary mask per label. When a label is
assigned to a block it is added to the corresponding
mask. When background is seen at a block, the cor-
responding blocks of all the masks are emptied. The
interest in having multiple labels can be observed on
figure 1.
Figure 1: A mask is used for each label to store the sta-
tionary objects. Thus, we know which are the visible and
occluded parts of each object. The visible parts of station-
ary objects are coloured.
4 MULTI VIEW MATCHING
4.1 General Intuition
With a large baseline, objects may have a very dif-
DETECTION AND LOCALISATION OF STATIONARY OBJECTS WITH A PAIR OF PTZ CAMERAS
593

ferent appearance in the two cameras and therefore it
cannot be used as a matching criterion.
Being given a pair of camera and a 3D object
there exists at least two points, called frontier points
(Cipolla et al., 1995) which are visible by the two
cameras. These points are the points of the object for
which the epipolar planes are tangent to the surface
of the object. In rectified images the top and bottom
points are frontier points. These points are the con-
straint we use in our matching criterion.
Because of segmentation errors and differences in
view point there is not necessarily only one silhouette
per object (and reciprocally). Thus, one to one silhou-
ette associations is not sufficient to fit the complexity
of the task. We propose to build a graph representing
associations between frontier points instead of silhou-
ettes.
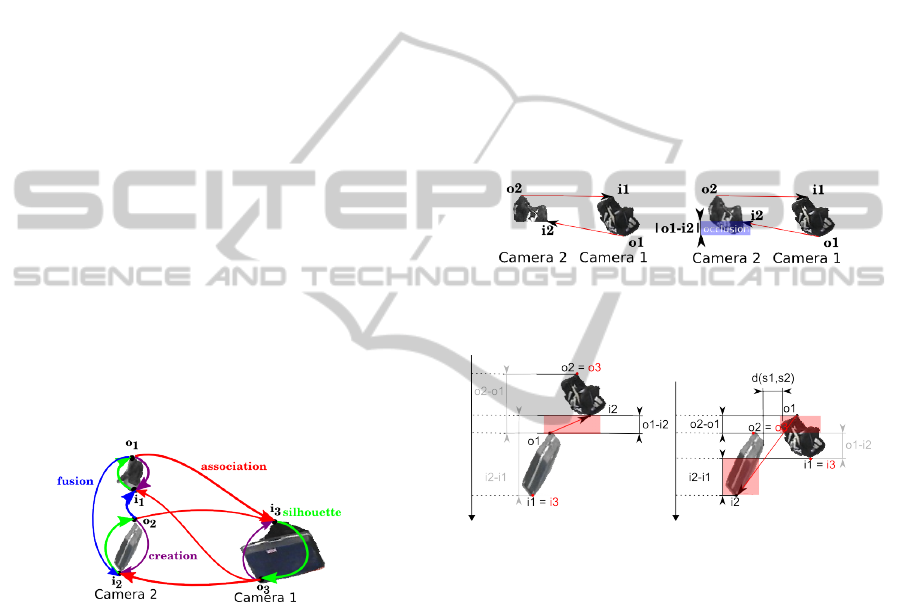
4.2 Graph Construction
We propose to make associations between frontier
points rather then directly matching silhouettes. To
this aim we build a directed graph, as illustrated on
figure 2, to model the authorised associations in such
a way that an object (or association of silhouettes) is
represented by a cycle. There are four types of arcs,
they represent the different relations between frontier
points, and each of them is assigned a particular cost.
Figure 2: Directed graph of possible associations. Cycles
in the graph represent possible silhouette associations. The
entering and exiting frontier points are noted i
i
and o
i
.
Let us consider two silhouettes s
1
, s
2
and their re-
spective exiting and entering frontier points o
i
and i
i
.
The cost of a silhouette arc is zero. It enforces the
unity of the silhouette.
The cost of an association arc it is set to the angle
difference between the two epipolar planes in which
lie the two frontier points, as illustrated in figure 3. Its
expression is:
c
association
= |o
i
− i
j
| (7)
In order to help filter false matches, the associ-
ation cost of two frontier points is set to +∞ if the
resulting triangulated 3D point is over or below a pre-
defined altitude threshold.
The creation arc has to be selected when an ob-
ject is seen in only one camera, thus it is considered
fully occluded in the other camera and its cost is the
following:
c
creation
= |o
i
− i
i
| (8)
The fusion cost from silhouette s
1
to silhouette s
2
is defined in a similar way in equation 9. This cost is
illustrated figure 4.
c
f usion
= (o
2
−o
1
)
+
+(i
2
−i
1
)
+
+(o
1
−i
2
)
+
+d(s
1
, s
2
)
(9)
where (.)
+
= max(0, .) and d(s
1
, s
2
) is the dis-
tance between the two silhouettes in the rectified im-
age. This distance prevents the fusion of silhouettes
which are far apart in the image, in other terms we
consider that occlusions cannot be too large. This cost
is illustrated in figure 3.
Figure 3: Association cost for arc o
1
→ i
2
. |o
1
− i
2
| repre-
sents the angular cost of an occlusion. Situation on the left
is can be interpreted as the situation on the right.
Figure 4: Illustration of the cost of the two possible fusion
arcs (in red) for a pair of silhouettes. The non active costs
are greyed, the active costs are highlighted by red rectan-
gles. The entering and exiting frontier points of the result-
ing “virtual” silhouette are i
3
and o
3
.
4.3 Optimisation
In section 4.2 objects were represented by a cycle in a
graph and each arc was assigned a cost. The cost as-
sociated to an object is therefore the sum of the costs
the arcs of the cycle. Finally finding the best matching
between silhouettes from the two cameras is equiva-
lent to finding the vertex disjoint cycle cover of the
graph of minimal cost. The cost of a cycle cover be-
ing the sum of the costs of all its cycles.
The number of cycle covers exponentially grows
with the number of silhouettes. Thus we propose a
simple heuristic to find an approximate solution. A
random node n is selected and the shortest cycle start-
ing from this node is computed using the Dijkstra al-
gorithm. Nodes selected in the cycle are then removed
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
594

from the graph. The process is repeated until all nodes
are selected.
5 EXPERIMENTS
This section is divided into two parts. First, the de-
tection of stationary objects is evaluated in the usual
context of single static cameras. In the second part
the matching algorithm is evaluated for a pair of PTZ
cameras.
The stationary object detection is first tested on
public sequences (I-Lids dataset for AVSS2007), then
on sequences more challenging in terms of occlu-
sions.
For the AVSS2007 dataset we consider that an ob-
ject is stationary 60 seconds after it has been seen for
the first time and remains at the same place. The re-
sults and ground truth values can be found in table 1.
Table 1: Detection results on the I-Lids 2007 dataset.
Sequence
name
Start time (s) End time (s)
Ground
truth
Detected Ground
truth
Detected
AB Easy 2:20 2:20 3:14 3:18
AB Medium 1:58 1:58 3:02 3:03
AB Hard 1:51 1:52 3:07 3:11
PV Easy 2:48 2:48 3:15 3:21
PV Medium 1:28 1:28 1:47 1:56
PV Hard 2:12 2:12 2:33 2:35
The algorithm is also tested on other sequences
which are made to provide more challenging scenar-
ios in terms of occlusions and object labelling. These
sequences show stationary objects which are always
partially occluded and stationary objects occluding
other objects.
Figure 5 shows that our algorithm performs well
at grouping with the same label the blocks of a sta-
tionary object, even if this object is always partially
occluded.
Figure 6 shows the influence of the
pIncompatibility penalty and of the pairwise
term V
i j
. The baggage is correctly segmented because
both objects did not appear at the same time. On the
overlap region both label have the same unary cost.
It is therefore the pairwise term, with λ
2
> 0 which
translates a notion of age consistency, which gives
the desired segmentation.
The second part of the experiments concerns
stereo matching. Sequences are acquired by PTZ
cameras, each performing a guard tour of approxi-
mately 15s. Thus, the cameras are highly unsynchro-
nised and parts of the scene are refreshed at a very low
frame-rate.
Figure 5: This sequence of images shows a partially oc-
cluded stationary object. Even in this case where the age of
the baggage is not the same for all the blocks only one label
is assigned.
Figure 6: Effect of the binary term on the segmentation.
Top line: λ
2
= 0, the criterion of similarity in age is not
active, the occluding object is not fully segmented. Bottom
line: λ
2
> 0, the criterion of similarity in age is active, the
segmentation is correct.
The first set of sequences is acquired indoor, it
shows an important difference in the point of view
of the two cameras as well as high degrees of occlu-
sion, as it can be seen in figure 7. Figure 7(a) gives
an example of object detected as two silhouettes. One
can see that the silhouettes 1 and 2 are linked by a fu-
sion arc and are correctly matched with silhouette 5
from the other camera. On figure 7(b) the bag repre-
sented by silhouettes 1 and 4 is almost fully occluded
in the left camera but they are nevertheless correctly
matched.
The second set of sequences is acquired outdoor
and shows a non planar scene, as objects can be put
on the window ledge. It is 1.35m high but this infor-
mation is not know a priori. The baseline between the
two cameras is 13m, there altitudes are 4.70m each,
and the objects in the scene are between 15m and 20m
from the cameras. The guard tour of each camera
is composed of 8 views. Figure 8(a) shows correct
matching in a case of strong occlusion. The suitcase
represented by silhouette 0 is severely occluded in the
left camera, only its top and the handle is visible. Our
approach based on stereo-geometry allows to success-
fully find the associations which best explains the ob-
servations using a 3D criterion.
Table 2 shows the precision and recall scores com-
puted on the four previous sequences. To be de-
tected, objects need to be observed in both cameras.
Thus this approach does not increase the recall but
increases the precision. This is essential for real case
application as the disturbance rate of the operators has
to be as low as possible.
DETECTION AND LOCALISATION OF STATIONARY OBJECTS WITH A PAIR OF PTZ CAMERAS
595

(a) Correct case of fusion of silhouettes 1 and 2.
(b) Despite the almost total occlusion, silhouettes 4 and 1 are correctly
matched.
Figure 7: Rectified panoramas from a pair of PTZ cameras.
Stationary objects are given an id. The straight lines are arcs
the of selected cycles and therefore correspond to frontier
points associations.
(a) Correct fusion and matching of a highly occluded non flat object (0 ↔
3 ↔ 4). An object at a height z 6= 0 is also correctly matched.
(b) Example of correct matches.
Figure 8: Rectified panoramas from a pair of PTZ cameras.
Stationary objects are given an id. Lines correspond to fron-
tier point associations
Table 2: Comparison of statistics computed on sequences
with a single-camera and a multi-camera approach.
Sequence Single-camera Multi-camera
Recall Precision Recall Precision
Interior 1 0,99 0,63 0,99 0,88
Interior 2 1 0,63 0,93 0,80
Exterior 1 0,95 0,86 0,95 0,92
Exterior 2 0,95 0,81 0,91 0,81
6 CONCLUSIONS
In this article we presented a novel approach for
the detection of stationary objects using a pair of
PTZ cameras. We successfully applied our detec-
tion and segmentation algorithm on challenging se-
quences. The obtained object silhouettes are used in
a matching phase increase the detection precision, but
also allow the computation of 3D position and height.
This matching stage was proved to be robust to severe
occlusions and segmentation errors.
REFERENCES
Alahari, K., Kohli, P., and Torr, P. H. S. (2008). Re-
duce, reuse & recycle: Efficiently solving multi-label
MRFs. In CVPR.
Bayona, A., SanMiguel, J., and Martinez, J. (2009). Com-
parative evaluation of stationary foreground object de-
tection algorithms based on background subtraction
techniques. In AVSS.
Bayona, A., SanMiguel, J., and Martinez, J. (2010). Sta-
tionary foreground detection using background sub-
traction and temporal difference in video surveillance.
In ICIP.
Beynon, M. D., Van Hook, D. J., Seibert, M., Peacock, A.,
and Dudgeon, D. (2003). Detecting abandoned pack-
ages in a multi-camera video surveillance system. In
AVSS.
Cipolla, R., Astrom, K., and Giblin, P. (1995). Motion from
the frontier of curved surfaces. In ICCV.
Fleuret, F., Berclaz, J., Lengagne, R., and Fua, P. (2008).
Multicamera people tracking with a probabilistic oc-
cupancy map. PAMI.
Guillot, C., Taron, M., Sayd, P., Pham, Q.-C., Tilmant, C.,
and Lavest, J.-M. (2010). Background subtraction for
ptz cameras performing a guard tour and application
to cameras with very low frame rate. In ACCV VS.
Guler, S., Silverstein, J., and Pushee, I. (2007). Stationary
objects in multiple object tracking. In AVSS.
Khan, S. M. and Shah, M. (2009). Tracking multiple oc-
cluding people by localizing on multiple scene planes.
PAMI.
Liao, H.-H., Chang, J.-Y., and Chen, L.-G. (2008). A lo-
calized approach to abandoned luggage detection with
foreground-mask sampling. In AVSS.
Mathew, R., Yu, Z., and Zhang, J. (2005). Detecting new
stable objects in surveillance video. In Multimedia
Signal Processing, Workshop on.
Miezianko, R. and Pokrajac, D. (2008). Localization of de-
tected objects in multi-camera network. In ICIP.
Porikli, F., Ivanov, Y., and Haga, T. (2008). Robust
abandoned object detection using dual foregrounds.
EURASIP J. Adv. Signal Process, 2008.
Utasi, A. and Csaba, B. (2010). Multi-camera people local-
ization and height estimation using multiple birth and
death dynamics. In ACCV VS.
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
596