
FAST PROTOTYPING OF EMBEDDED IMAGE PROCESSING
APPLICATION ON HOMOGENOUS SYSTEM
A Parallel Particle Filter Tracking Method on Homogeneous Network of
Communicating Processors (HNCP)
Hanen Chenini, Jean Pierre Derutin and Thierry Chateau
LASMEA-UMR 6602 CNRS, Blaise Pascal University, 24 Av. DesLandais, Clermont-Ferrand, France
Keywords:
Face Tracking, K-Nearest Neighbor (KNN), Parallel Implementations, Homogeneous Network of Communi-
cating Processors.
Abstract:
This article discusses the design of an application specific MP-SoC (Multi- Processors System on Chip) ar-
chitecture dedicated to face tracking algorithm. The proposed algorithm tracks a Region-Of-Interest (ROI)
by determining the similarity measures between the reference and the target frames. In our approach, this
measure is the estimation of the Kullback-Leibler divergence from the K-nearest neighbor (KNN) framework.
The metric between pixels is an Euclidean norm in a joint geometric and radiometric space. The adopted
measure allows us to check if the regions have similar colors and also if these colors appear at the same
location. Considering the necessary computation amounts, we propose a parallel hardware implementation
of the developed algorithm on MP-SoC architecture. Creating multiple processors in one system is hard for
software developers using traditional hardware design approaches due to the complexity to design software
models suitable for such FPGA implementations. In order to deal with this problem, we have introduced a
CubeGen tool to avoid fastidious manual editing operations for the designer. This new methodology enables
us to instantiate a generic Homogeneous Network of Communicating Processors (called HNCP) tailored for
our targeted application. Our implementations are demonstrated using the Xilinx FPGA chip XC6VLX240T.
1 INTRODUCTION
We will provide a brief introduction to particle filters
(PFs), as their application and implementation is the
focus of this article.
In most of the application, prior knowledge about
the phenomenon being modeled is available. This
knowledge allows us to formulate bayesian models.
Within this setting, we used the Monte-Carlo simu-
lation methods (particle filtering) in order to imple-
ment the bayesian framwork (Chen, 2003). PFs are
Bayesian in nature and their goal is to find an approxi-
mation to the posterior density of the states of interest
(e.g. position of a moving object in tracking) based
on observations corrupted by additive gaussian white
noise which are inputs to the filter. This is done using
the principle of Importance Sampling (IS) whereby,
multiple copies (particles) of the variable of interest
are drawn from a known density (Importance Func-
tion (IF)), each one associated with a weight that sig-
nifies the quality of that specific particle based on the
received observations. An estimation of the variable
of interest is obtained by the weighted sum of all the
particles.
The main objective of particle filtering (Maskell
and Gordon, 2001) is to track a variable of interest as
its evolves over time t, typically with nonlinear mod-
els and non-gaussian noises. Consequently, they have
been used in a wide variety of real-time applications
including tracking. Tracking is a process measure-
ment to sequentially estimate hidden states s
t
from all
the available measurements z
t
(observations). An ef-
ficient and robust tracking of objects in complex en-
vironments is important for a variety of applications
relying on tracking including surveillance and moni-
toring (Xinyu and Baoxin, 2005), autonomousdriving
(Petrovskaya and Thrun, 2009), medical imaging (De
Bruijne and Nielsen, 2004) or robotics. Depending
on the state-space model proposed, the complexity is
related to the prediction of M sampled particles and
weight evaluation stage.
The proposed algorithm considered in our ap-
proach, uses a Gaussian approximation to the full-
posterior as the importance function. Also, we pro-
122
Chenini H., Pierre Derutin J. and Chateau T..
FAST PROTOTYPING OF EMBEDDED IMAGE PROCESSING APPLICATION ON HOMOGENOUS SYSTEM - A Parallel Particle Filter Tracking
Method on Homogeneous Network of Communicating Processors (HNCP).
DOI: 10.5220/0003828401220133
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 122-133
ISBN: 978-989-8565-04-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

pose to compute the Kullback-Leibler distance using
the KNN framework to evaluate likelihood that fur-
ther increases the complexity of the algorithm. To
sum up, the proposed particle filter algorithm consists
of an initialization of the template model and a se-
quential Monte Carlo implementation of a Bayesian
filtering for the stochastic tracking system.
Translating an algorithm for real-time implemen-
tation requires making specific choices so that the de-
sign meets the constraints. Some of the main con-
straints are speed of execution, power dissipation, ac-
curacy of the results, cost and time involved in the
implementation. Dedicated hardware implementation
may be useful for high speed processing but it does
not offer the flexibility and programmability required
for system evolution. Applications with stringent
resource-consumption and runtime constraints are in-
creasingly resorting to MP-SoC architectures. Gen-
erally, the MP-SoC architecture has become a solu-
tion for designing embedded systems dedicated to ap-
plications that require intensive computations. In the
MP-SoC architecture, the mapping of software tasks
to hardware resources is important since it affects the
degree of parallelism among multiple processors and
the utilization of hardware resources.
Except for the state estimate and initialization
stage, processing of individual particles can be done
in parallel. With regard to the latter, we applied
our design technique to implement the proposed face
tracking algorithm on the homogeneous MP-SoC ar-
chitecture (Si´eler et al., 2010). This parallel architec-
ture contains multiple homogenous processors, mem-
ory blocks, DMA (Direct memory access) and several
I/O resources in the same chip. In addition, it can be
beneficial to take advantage of the parallelism, low
cost, and low power consumption offered by FPGAs.
The design and implementation of a real-time object
tracking algorithm on a FPGA focuses on minimiz-
ing resource utilization to allow functionality of the
application that uses the tracking information to be
added. We then propose a FPGA implementation to
evaluate real-time performance of the developedalgo-
rithm. The details of this implementation are provided
in section 4.
The rest of the paper is organized as follows. Sec-
tion 2 describes the theory behind the PFs and the sur-
vey of existing related efforts. In Section 3, we briefly
describe and present the face tracking algorithm with
particle filter framwork, including face model, dy-
namic model and observation model. Section 4 is
mainly concerned with outlining our proposed design
flow for implementing the developed image process-
ing application. Evaluation of resource utilization and
latency of the two parallel schemes on FPGA platform
to speed up the tracking process is presented in sec-
tion 5. Section 6 concludes the paper.
2 STATE OF THE ART
Sequential Monte Carlo (SMC) (Diaconis, 2003)
methods are a set of simulation based methods which
provide a convenient and attractive approach to com-
puting the posterior distribution. Therefore, SMC
methods are very flexible, easy to implement, par-
allelizable and applicable in very general settings.
Several closely related algorithms under the names
of bootstrap filters, the Sampling Importance Re-
sampling Filter (SIRF), condensation, particle filters,
Monte Carlo filters, Sequential Importance Sampling
(SIS) and interacting particle approximation have ap-
peared in several research fields. The problem en-
countered by the SIS is that, as time t increases, the
distribution of the importance weights becomes more
and more skewed. Practically, after a few time steps,
most particles have negligible weights. To avoid this
degeneracy, the key idea of SIR (Bootstrap filter) is
to eliminate or replicate particles depending on their
importance weight (Particles with high weight are se-
lected more and more often, others die out slowly).
PFs (Maskell and Gordon, 2001) are used to per-
form filtering for dynamic state-space problem that
can be described as a sequential representation (sys-
tem transition equation and observation equation).
State-space model depends on physics of this prob-
lem.
In most practical scenarios, these models are non-
linear and the densities involved are non-Gaussian.
PFs are used to estimate states of a nonlinear, non-
Gaussian state space model. Traditional filters like the
Extended Kalman Filter (Greg and Gary, 1995), ex-
tension of Kalman filter, are known to find an optimal
solution for the recursive problem if state and/or mea-
surement models are nonlinear, and state and mea-
surement noises are non-Gaussian.
In our implementation, we choose to use the
problem modeled as Markovian nonlinear and non-
Gaussian state space. Often, in practical operations, a
large number of particles need to be used for comput-
ing estimates of the desired state. Hence for meeting
speed requirements of real time applications, it is nec-
essary to have high throughput designs with ability to
process a larger number of particles in a given time.
Parallelizability is the key to high throughput design
for PFs, as this enables simultaneous processing of
particles.
In the digital implementation of PFs algorithms,
the choices available are to either use a digital sig-
FAST PROTOTYPING OF EMBEDDED IMAGE PROCESSING APPLICATION ON HOMOGENOUS SYSTEM - A
Parallel Particle Filter Tracking Method on Homogeneous Network of Communicating Processors (HNCP)
123

nal processor (DSP), a field-programmable gate array
(FPGA) or an application specific IC (ASIC).
Recently, many approaches on the hardware im-
plementation of particle filters have drawn attention
(Boli´c et al., 2004), resulting in an FPGA prototype
for a particle filter algorithm. As part of that effort,
the authors have developed an architecture for a dig-
ital hardware implementation of particle filters along
with efficient resampling algorithms. Their initial at-
tempt was evaluated on TI TMS320C54x DSP for
bearings-only tracker algorithm. With M = 2000 par-
ticles, on a single state-of-the-art DSP, yielded speeds
of up to 500Hz for SIRF. By using a Xilinx Virtex II
Pro FPGA, they achieved a maximum sampling fre-
quency of 50 kHz for a similar application. This later
led to an application specific integrated circuit (ASIC)
implementation for realizing certain stages in the par-
ticle filter algorithm.
The successful implementation of this kind of im-
age processing algorithm illustrates that the digital
signal processing required for high rate sensing appli-
cation can be efficiently implemented on FPGA hard-
ware(Xilinx Spartan-II XC2S200) (Boli´cet al., 2004).
In parallel implementations, propagation and
weight calculation for different particles are indepen-
dent and each requires M iterations for one PF recur-
sion. The resampling, which is inherently sequen-
tial, has been modified in order to allow for parallel
implementation. As resampling requires all particle
weights to be available; complete parallelization of
the particle filter algorithm is difficult. Efficient meth-
ods to address this in hardware can be found in (Boli´c,
2004). More recently, a Single Instruction Multiple
Data (SIMD) architecture that uses N processors to
process M particles for particle filters has been pre-
sented in (Medeiros et al., 2008). Other interesting
implementation strategy was done using General Pur-
pose Graphical Processing Units (GP-GPUs). In (Liu
et al., 2010), the authors explored the implementation
of multi-cue based face tracking algorithm on dedi-
cated processors and demonstrated the efficiency of
two parallel computing techniques (one is multicore
based parallel algorithm with a MapReduce thread
model and the other is GPU based speedup approach).
For human tracking according to (Anastasios and
Nikolaos, 2012), they apply the Service Oriented
(SOA) Architecture framework for scheduling com-
plex industrial workflows in particular a real-time
self-initialized human tracking based on Particle Fil-
ter under complex observation conditions. Durant the
exploration of the unknown environment, the tracker
position maintains a set of hypotheses with regard to
the last position of the tracked object and the dif-
ferent objects around it that have similar colors and
shapes. The input for updating the tracker position
comes from the various sensors cameras distributed
placed in critical parts of the industries (Nissan Iber-
ica Automobile Construction company). Moreover,
the estimate of the position of the tracked object can
be updated based on the dataset collected up to that
point in time.
3 FACE TRACKING WITH
PARTICLE FILTER
3.1 Particle Filter
Our goal is to track the face through a sequence of
video. Tracking objects in video involves the mod-
eling of non-linear and non-gaussian systems. The
particle filter can be employed by using a probabilis-
tic framework which formulates tracking problems as
a Hidden Markov Model (HMM).
The state of face at time t is donated s
t
, which
represents unobserved state (hidden position) of the
object, and its history is S = {s
1
...s
t
}. Similarly, the
temporal data sequence (images) features at time t is
z
t
with history is Z = {z
1
...z
t
}.
From a Bayesian perspective, the tracking prob-
lem is to recursively compute the posterior state-
density p(s
t
\z
t
) of the state s
t
at time t, taking differ-
ent values, given the data z
0:t
up to time t (using the
process density p(s
t
\s
t−1
) and the observation den-
sity p(z
t
\s
t
)). To sum up, the model is described by:
• p(s
0
) for t = 0
• p(s
t
\s
t−1
) for t > 0
• p(z
t
\s
t
) for t > 0
Given the face model, the tracking algorithm con-
sists of four main steps:
1)Sampling step, Generation of new particles, in
which M particles s
m
t
for m = {1...M} are generated
from old sample set s
m
t−1
using an importance function
ˆs
m
t
≈ π(s
t
\s
m
0:t−1
, z
t
) (1)
2) Weight measurement, assigns importance
weights ω
m
t
for each newly generated samples based
on the received observation. This step is the most
computationally intensive and generally involves the
computation of transcendental trigonometric and ex-
ponential functions.
ˆ
ω
m
t
∝ ω
m
t−1
P(z
t
\s
m
t
)P(s
t
\s
m
t−1
)
π(s
m
t
\s
m
0:t−1
, z
1:t−1
)
(2)
3) State estimation obtains the final state vector
of face by newly generated samples and its weights
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
124

4) Resampling step where the input is an array of the
weights of the particles and the output is an array of
indices of which particles are going to propagate for-
ward. The first three steps form the particle filter Se-
quential Importance Sampling (SIS) filter. The filter
that performs all the four operations is the Sample Im-
portance Resampling Filter (SIRF).
3.2 Tracking Application
The application is based on skin color detection which
is performed on the input image. A particle filter is
applied then for tracking the image position s
t
of the
region of interest (the face).
3.2.1 Skin Detection using Color
In the following, we present a conceptually simple
approach for face detection. Skin color (Vezhnevets
et al., 2003) is a distinguishing feature of human
faces. In a controlled environment, the skin detec-
tion can be efficient to locate faces in images. The
first step of the proposed algorithm is to detect the
human face in the first frame. Since we are interested
in tracking, we assume that the target object has been
detected using an intuitive method to find a rectangu-
lar region of the face. The skin detection technique is
summarized in figure 1. This method used the thresh-
olding of RGB color space for skin detection, seg-
mentation technique and region labeling in order to
separate the face region. The detected object become
reference template for the first frame and it is updated
in every frame.
Threshold
Image
segmentation
RGB colour image
Binary Image
Labelling
image regions
Separate
regions
Spatial Extraction
Final labelling Face region
Originale
Image
Figure 1: Face detection using skin color.
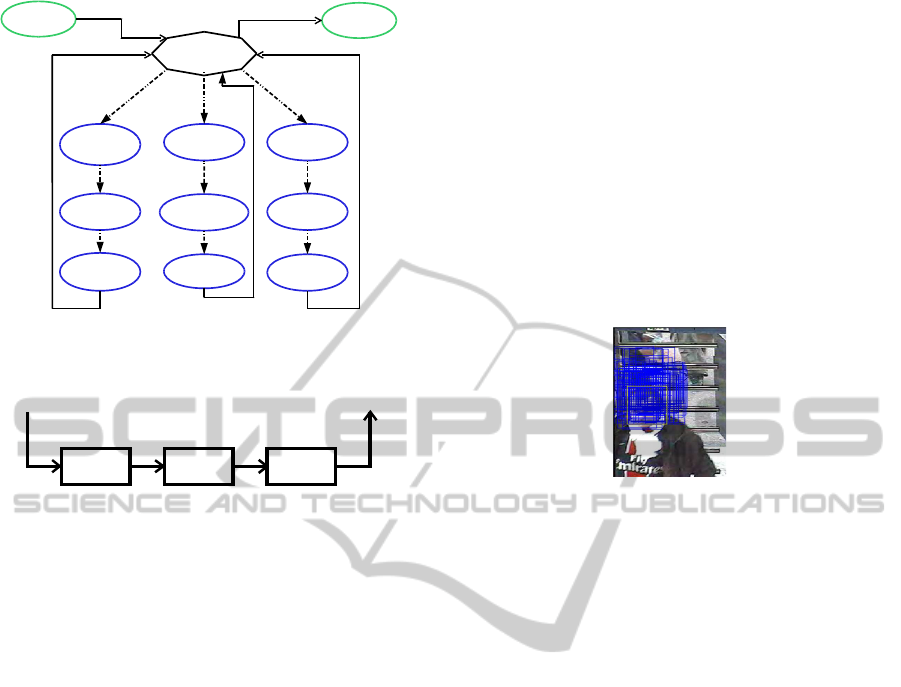
3.2.2 Color based Tracking Approach
We want to apply a particle filter in a color model
based framework. This system depends on the deter-
ministic search of a window (particle), whose color
content matches a reference color model. To model
Image Sequence
Frame 1
Frame 2
Frame 3
Frame 4
.............
Frame N
Generation of
Particles
Evaluation
Estimation
Resample
Weight of each particle
based on Kullback-Leibler
divergence
Select the location of the
target as a particle with
maximum weight
Kullback-Leibler divergence
K-Nearest Neighbors
[s^t , w^t]
[s^best , w^best]
[s^* , w^(-1)]
[s^* , w^(-1)]
Estimation
Evaluation
Measurement
Process
D_KL1
D_KL2
D_KL3
D_KLN
Figure 2: Particle filter scheme.
the target using color information, we pick M rectan-
gular regions {s
0
1
...s
m
t
} within the object to be tracked.
Each rectangle s
m
i
is represented by the mean (h, s, v)
color of the pixels within regions
m
i
(other color spaces
can be considered similarly). Since we use the SIRF
for our implementation, we obtain the optimal Impor-
tance distribution which is given by:
π(s
0:t
\z
0:t
) = p(s
t
\s
m
t−1
, z
t
) (3)
Consequently, the recurrence relations (1) and (2)
are simplified and formed the basis for the optimal
Bayesian solution:
• For the m
th
sample
s
m
t
≈ p(s
t
\s
m
t−1
) (4)
• For the m
th
sample, the weight assignment equa-
tion is :
ω
m
t
= ω
m
t−1
p(z
t
\s
m
t
) (5)
Figure 2 outlines an iteration of the particle fil-
ter algorithm. The performance of the filter has been
tested on a rolling ball sequence. The actual frame
(example we take here frame 2) of the sequence is
loaded and M samples are taken using (x, y) position
of upper-left corner stored in each particle.
In the first iteration, this sampling is randomly
generated from a uniform posterior probability den-
sity. In a measurement process, M windows are cap-
tured from the image using the coordinates given by
the previous sampling stage. Particle weights com-
putation is based on the distinctive features that can
be followed from frame to frame around the region
of interest instead of performing an exhaustive search
over the whole image. In order to improve weights
computation, we have chosen to get an estimation of
the Kullback-Leibler divergence from the K
th
Near-
est Neighbor (KNN). The particle with the maximum
weight s
max
t
is selected as best candidate for the state
of the system in the iteration. In order to track mov-
ing objects efficiently, we perform a resampling stage
(see Figure 2) evaluating previous particle weights
FAST PROTOTYPING OF EMBEDDED IMAGE PROCESSING APPLICATION ON HOMOGENOUS SYSTEM - A
Parallel Particle Filter Tracking Method on Homogeneous Network of Communicating Processors (HNCP)
125

and concentrating particles around the most proba-
ble states, discarding those with lower weights. A
detailed description of the particle filter algorithm is
presented in the following sections.
3.2.3 Face Model
We are used a rectangle region to describe face fea-
tures for tracking. In our methods, the face model is
defined by:
P
t
= α
x
P
x
+ α
y
P
y
+ α
h
P
h
+ α
s
P
s
+ α
v
P
v
(6)
where α
x
, α
y
, α
h
, α
s
and α
v
are the confidence values
of the 2D position (x, y) and color space (H, S,V) re-
spectively. The values can be determined empirically
by human. The combination of the color information
and the evolution of the 2D position achieve excellent
performance in term of speed and accuracy.
To define the problem of tracking, we consider
that the state sequence s
t
of a target given by: s
t
=
{X
t
,Y
t
,W, H} where s
t
is a rectangle which represents
the region-of-interest (ROI), where (X
t
,Y
t
) is the po-
sition of upper-left corner of the rectangle and W, H
are the width and the height of the rectangle respec-
tively. For subsequent frames, the tracking algorithm
confines its search space to an area centered on the
location found in the previous frame. The implemen-
tation details are described in the following section.
3.2.4 Evolution and Observation Model
We consider a dynamic system represented by the
stochastic process s
t
whose temporal evolution is
given by the state equation as shown in equation (8)
(Face dynamics are modeled as a first order process,
as shown in equation):
s
t
= s
t−1
+ Ω
t−1
(7)
where Ω
t−1
indicates the Gaussian noises.
Since we use the SIRF for our implementation,
the observation model is performed to measure the
weight for all the newly generated samples (which in-
cludes two given information based on color features
and movement features). We want to estimate the
state vector s
t
at discrete times with the help of system
observations which are realizations of the stochastic
process z
t
governed by the measurement equation.
The observations are available at discrete times ac-
cording to:
p(z
t
\s
t
) ≈ exp(−µD
kl
) (8)
where D
kl
is the Kullback-Leibler divergence be-
tween the reference and the target frames. The aim
of the likelihood distribution p(z
t
\s
t
) is to determine
in successive frames the regionwhich best matches, in
terms of a similarity measure. This similarity between
the template and the current image can be measured
by the distance between them. As we will see later,
this distance is expressed from the samples using the
K
th
Nearest Neighbour framework (KNN).
3.2.5 The K
th
Nearest Neighbor(KNN)
Classically, distance can be a distance between color
histograms or, similarly, probability density func-
tions (PDFs). For example, the Bhattacharya distance
was used for tracking (Johncy Rani and Suja Priyad-
harsini, 2010). Another widely used similarity mea-
sure is the Kullback- Leibler distance (Boltz et al.,
2009):
D
kl
(R, T) =
Z
R
f
T
(s)
log( f
T
(s))
log( f
R
(s))
ds (9)
Distance (10) can be decomposed as follows:
D
kl
(R, T) =
Z
R
f
T
(s)log( f
T
(s))ds
−
Z
R
f
T
(s)log( f
R
(s))ds
= −H(T) + H
X
(T, R)
(10)
where H is the differential entropy and H
X
is the
cross entropy, also called relative entropy or likeli-
hood.
In our approach, the reference frame and target frame
from the video frames are selected first. Then the par-
ticular Region-of-Interest (RoI) is selected from the
reference frame and the (Y,U,V) colour feature was
extracted. Then, the colour and the geometric features
are extracted from the target frame. Finally, the Kull-
back Leibler Divergence is used for finding the sim-
ilarity measure between the reference and the target
frames.
In this paper, we propose to compute the
Kullback- Leibler distance between high-dimensional
PDFs using the K
th
Nearest Neighbor framework
(KNN). Since the Kullback- Leibler is a distance, the
KNN-based expression of the Kullback-Leibler dis-
tance proposed for RoI tracking is the difference be-
tween a cross entropy and differential entropy (Boli´c,
2004)(see Eq. (11)); the KNN estimate of this dis-
tance is given by:
D
kl
(T, R) = H
X
KNN
(T, R) − H
KNN
(T)
= log(
|R|
|T − 1|
) +
d
|T|
∑
s∈T
log(
ρ
k
(R, s)
ρ
k
(T, s)
)
(11)
where ρ
k
(R, s), ρ
k
(T, s) are the distance to the K
th
nearest neighbor of s in R and T respectively exclud-
ing the sample located at s if any.
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
126

U
4
U
0
U
1
U
2
U
3
CSW
0
CSW
2
CSW
1
CSW
3
CSW
4
0
1
2
3
4
0
0
3
3
3
Figure 3: Systematic resampling with non-normalized
weights (M=5).
3.2.6 Systematic Resampling in SIR
The particles are resampled to generate an un-
weighted particle set according to their importance
weights to avoid degeneracy. This is done by mul-
tiplying or discarding particles with respect to high or
low importance weights to obtain a predefined num-
ber of particles.
Standard algorithms used for resampling such
as residual resampling (RR), branching corrections
(Crisan et al., 1999), systematic resampling (SR)
(Boli´c, 2004)...The proposed algorithm in this paper
uses the systematic resampling algorithm. This is the
most commonly used resampling algorithm for PFs
(Maskell and Gordon, 2001). The Resampled parti-
cles are drawn proportional to this distribution to re-
place the original set. The SR concept for a PF that
used 5 particles is shown in figure 3. First the cumu-
lative sum of weights (CSW) of sampled particles is
computed. Then, as shown on the y axis of the graph,
a function u(m) called the resampling function is sys-
tematically updated and compared with the CSW of
the particles. The corresponding particles are repli-
cated to form the resampled set which for this case is
{x(0), x(0), x(3), x(3), x(3)}. This method eliminates
particles with low weight and keeps more particles in
more probable regions.
3.3 The Proposed Particle Filter
Algorithm
Initialization. For most object tracking system, ini-
tialization algorithm is only performed at the begin-
ning of tracking which is an independentprocess from
the tracking process. In this tracking system, we have
developed an algorithm which will be introduced to
achieve automatic initialization and the face detected
is used as the reference face model. We assume in
our approach the image to be recorded with station-
ary camera.
Algorithm Description. We can now specify the al-
gorithm in detail as fellows. The face tracking algo-
rithm is separated into two main stages: automatic ini-
tialization and particle filter tracking. The principle of
the proposed algorithm is described in detail bellow.
1. Initialization(automatic)
Reference face template updating.
2. Particle filter tracking:
Using cumulative measurement up to time
t, Z = (z
1
...z
t
) , our aim is to estimate
[s
m
t
, ω
m
t
]
M
m=0
= Function([s
m
t−1
, ω
m
t−1
]
M
m=0
, z
t
)).
• Simulate M independent and identically dis-
tributed random samples (Randomly cho-
sen particles to represent posterior distribu-
tion by generating a random number δ
x
∈
]−0.5, 0.5[, δ
y
∈ ]−0.5, 0.5[ uniformly dis-
tributed). [s
m
t
, ω
m
t
]
M
m=0
(where ω
m
t
are the as-
sociated weights and M is the number of par-
ticles). Given the observed data z
t
at t, for each
particle m = 0...M do:
• Calculate face model.
• Calculate Euclidean distance between the sam-
ple feature vector P
t
and the reference feature
vector P
r
.
• Calculate Kullback- Leibler distance.
• Weight measurement: For the m
th
, we obtain
its weights ω
m
t
by a Kullback- Leibler
similarity function as shown in Equation (10).
So we obtain the final weight for the m
th
as:
ω
m
t
≈ exp(−µD
kl
)
3. Estimating state parameters at time step: calcu-
late mean position of each target using a weighted
average of the particles.
4. Resampling step [s
m
t
, ω
m
t
]
M
m=0
to obtain new set of
particles [s
m
t
,
ˆ
ω
m
t
]
M
m=0
(using the above-mentioned
resampling algorithm).
4 PARALLEL PARTICLE FILTER
ALGORITHM
4.1 Homogeneous Network of
Communicating Processors
Due to the increasing complexity of MPSoC architec-
tures, software and hardware designers as well as sys-
tem architects are facing completely new challenges.
Optimization of interconnects among processors and
memories becomes important as multiple processors
and memories can be integrated on a MPSoC since
FAST PROTOTYPING OF EMBEDDED IMAGE PROCESSING APPLICATION ON HOMOGENOUS SYSTEM - A
Parallel Particle Filter Tracking Method on Homogeneous Network of Communicating Processors (HNCP)
127

it may target multiple objectives: application per-
formance, power consumption/energy, temperature,
small chip area, etc. Consequently, high performance
embedded design must aim to obtain an ideal balance
between hardware constraints and performance con-
straints. As well, developing processors network sys-
tems tailored to a particular application domain is crit-
ical and design-time consuming in order to achieve
high performance customized solutions. The effec-
tiveness of such approaches largely depends on the
availability of an ad hoc design methodology. Our
goal was to limit the phase of architecture exploration
in order to reduce design time and to allow fast proto-
typing.
Our research interests are based mainly on fast
prototyping tools which enable the parallelization of
real-time signal and image algorithms in a homoge-
neous communicating processor network. In this pa-
per, we propose a new optimized design methodol-
ogy under performance constraints. Based on Multi-
Processors concept, our approach proposes an orig-
inal design flow for the fast prototyping of image
processing on a MP-SoC architecture. Our HNCP
methodology is based on two essential concepts.
First, it consists in the derivation of a generic archi-
tecture based on a HNCP (Homogeneous Network
of Communicating Processors). The second feature,
parallelization of the sequential code on the differ-
ent soft-core performed using specific communication
functions based on Parallel Skeleton concept, such as
data, task and flow parallel skeletons. We believe that
our methodologyprovides several benefits such as im-
proving parallelism of tasks (or data), fast and valid
mapping of software models to hardware architecture.
4.1.1 The Proposed Multi-processors System on
Chip Design Methodology
The proposed methodology presents a generic MP-
SoC design flow dedicated to the fast prototyping of
complex image processing. This approach is based
on concepts of HNCP and parallel programming with
the use of specific communication functions. In the
following, we present the generic HNCP architecture
and how to configure it.
The HNCP (Homogeneous Network of Commu-
nicating Processors). Different models of paral-
lel architecture exist, we choose the MIMD-DM
model (Multiple Instruction Multiple Data with Dis-
tributed Memory). Communications between proces-
sors are done using the message passing communica-
tion model. We chose this architecture because of its
ability to execute a large range of parallel scheme ef-
ficiently (data and task parallelism, pipeline). The
interconnection network is a static network with reg-
ular hypercube topology. This hypercube topology
eases scalability (when the number of processors is
doubled, the maximum distance D between two pro-
cessors and the number of links per node only in-
creases by 1) and routing which can be calculated us-
ing a simple combinatorial function.
This architecture is homogeneous. As seen from
the figure 4, each node comprises the same identi-
cal components (soft processor, with local memory
for application software and data storage, and a com-
munication device). All components can be chosen
inside a library of available custom components or
commercial IP. Depending on the application, an ar-
chitecture derived from the generic architecture may
differ from another through the different options and
parameters relating to the processor (optional arith-
metic units, implementation options), to the memory
(amount of local memory, size of potential buffers)
and to the interconnection network (type of link be-
tween processor, number of nodes).
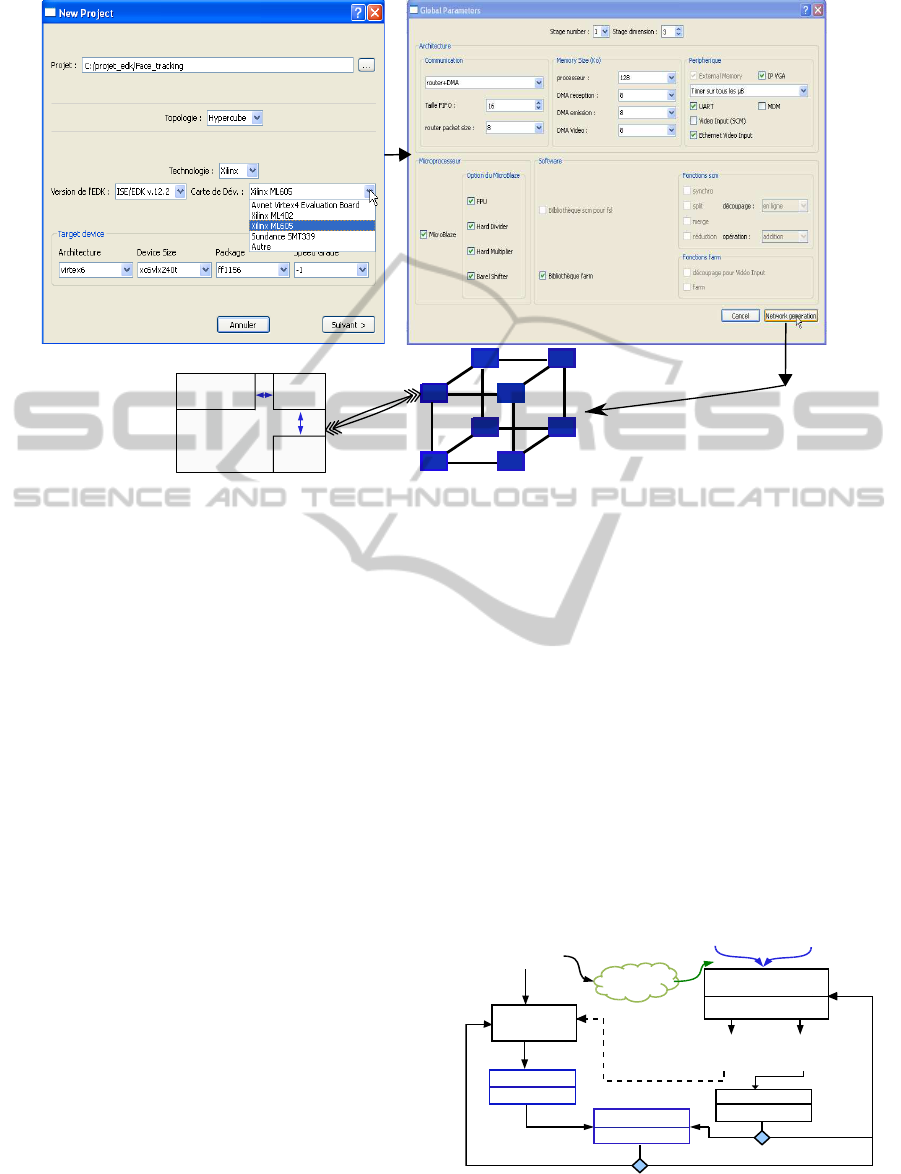
Architecture Generation and HNCP Configura-
tion Via CubeGen Tool. In order to reduce the time
and effort needed to design a network of communicat-
ing processors, we have developed a tool called Cube-
Gen(see figure 4). It enables to automate the configu-
ration file creation dedicated to the Embedded Devel-
opment Kit (EDK) of Xilinx company. This .mhs file
contains the description of the system with the con-
nection between the different IPs. The designer has
to specify, via a graphical interface, the different pa-
rameters chosen for the network: network dimension,
MicroBlaze parametrization, memory size allocated
to each processor,type of communicationlink and use
or not of the special IP for I/O (VHDL block designed
to control the I/O directly from the video flow).
CubeGen automates the high level description of
the HNCP in few seconds. The designer launches the
synthesis of the system with specific target to check if
this configuration of the HNCP can be implemented.
This methodology matches perfectly with the concept
of fast prototyping on SoPC. The designer obtains
quickly an architecture tailored for the target appli-
cation. Moreover, CubeGen provides a well-suited li-
brary (regarding architecture configuration choice) of
specific lightweight communication functions that fa-
cilitate conversion from sequential algorithm to a par-
allel C code.
Proposed Design Flow. The proposed design flow
(as shown in figure 5) takes as input a sequential al-
gorithm (written in C Code). Thanks to a CubeGen
tool, an Homogeneous Network of Communicating
Processors (HNCP) is automatically generated using
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
128
Communication
layers
Soft-
Processors
Memory
Details of each node
.mhs files
CubeGen Interface
Figure 4: GUI of the CubeGen tool.
a set of available IPs.
Parallelization process is based on the main idea
that most of parallel applications were built upon a
limited number of recurring schemes of paralleliza-
tion (called parallel skeletons). As we already men-
tioned, the proposed CubeGen tool generates specific
lightweight communication functions that are tuned
to the network configuration (number of processors,
communication links, parallelization scheme...). With
these communication functions, designer can convert
sequential algorithm into a parallel C code. Thus the
whole system is instantiated on SoPC Xilinx platform
(ISE/EDK tools). If HW architecture does not meet
area constraints, a first loop enables to re-configure
the HNCP thanks to CubeGen. Otherwise, the whole
system (SW and HW) can be tested on board or simu-
lated (using abstraction models for co-simulation). If
this final system does meet timing constraints, refin-
ing can be done on parallel code or/and on architec-
ture configuration in order to converge to a satisfying
solution.
4.1.2 Parallel Programming
Today’s challenge is to provide high-level program-
ming concepts without sacrificing efficiency. How-
ever, the programming level is still rather low and
programmers have to manage low level communica-
tion problems such as deadlocks. Moreover, the pro-
gram is split into a set of processes which are assigned
to the different processors. As described in previ-
ous section, the proposed approach tries to increase
the abstraction level of parallel programming and to
overcome the mentioned issues. The designer can de-
fine easily and quickly a suited HNCP for the appli-
cation but software development still remains to pro-
gram the differentsoftcores. In order to tackle parallel
programming and communications aspects, we have
developed a set of specific skeletons and the associ-
ated communication functions. They suit perfectly
to the network topology and ease the designer works
(abstraction level). From a specific network config-
uration (size of hypercube an communication links),
a library of functions are automatically generated by
CubeGen (see figure 5) for all skeletons. The map-
ping and the scheduling of the skeletons are static and
are realized during the compilation. In this paper,
we investigate the approach of parallelization Farm
scheme.
Synthesis
ISE/EDK
Modelsim
Simulation, Validation
Architecture
Generation
Parallel
Programming
Compilation
GCC
Parallel
Skeletons
CUBEGEN
Sequential
Algorithm
Available
IP
Library of
communication
function .c
HNCP
description
.mhs
Configuration
choice
Figure 5: The proposed design flow.
Parallel Skeleton Farm. In practice, we generate
FAST PROTOTYPING OF EMBEDDED IMAGE PROCESSING APPLICATION ON HOMOGENOUS SYSTEM - A
Parallel Particle Filter Tracking Method on Homogeneous Network of Communicating Processors (HNCP)
129

M number of particle in the region of high interest
(i.e. around the Region of Interest RoI) for each iter-
ation. This search window is variable from one frame
to another. Therefore, we will focus to implement
our tracking algorithm using dynamic data with the
enhanced Farm skeleton provided by our skeleton li-
brary. Farm skeleton may use either a static load dis-
tribution or a dynamic load distribution (Poldner and
Kuchen, 2008). Since our approach is based on reg-
ular homogeneous architecture, we are interested to
the case where the master sends new data to any slave
whenever his previous work is completed. It consists
of a master entity and multiple workers. In a dynamic
data parallel implementation, the master decomposes
the input data in smaller independent data sets and
sends them to each worker. Workers process the data
and send their result to the master which merges them
to get the final result as depicted in figure 6.
Worker
Master
Worker
Partial Result
Partial Result
Data set
Data set
Figure 6: Farm skeleton.
Our skeleton library offers a pre-implemented
function dedicated to farm implementation for ini-
tialisation (init-farm), synchronisation (synchro) and
work distribution (farm) as depicted bellow. The de-
signer can use directly these functions to shorten par-
allel programming.
init_farm(); //Initialization
synchro(); //the master node sends synchronization
//pulses to slave nodes to wake up.
while(proc_retour < Nb_max_of_Data)
//number of data to be sent is Nb_max_of_Data.
microblaze_disable_interrupts();
if(image_comp > 0)
image_maitre=image_comp;
if(image_maitre==image_comp)
image_comp--;
microblaze_enable_interrupts();
//Block the send or the receive until
//the slave executes the task and delivers the result
//back to the master.
compute _function_master
//The master itself process the next data.
microblaze_disable_interrupts();
//Wait for the request to send or to receive.
farm();
//Receive/send incoming data(outgoing data
from/to slave.
microblaze_disable_interrupts();
4.2 Parallel Particle Filter Algorithm on
HNCP
In our implementation of facetracking algorithm, sev-
eral independent parallel data (particles) are gener-
ated. A straight-forward method to apply the farm
skeleton with this specific application is to associate a
work element for each generated particle since all the
particles are independents .
In this way, the remaining sequential algorithm
part in the parallel algorithm (sample generation and
resampling steps) represents a minor part of the pro-
cessing time in the sequential implementation (see
section V) thus allowing an efficient parallel im-
plementation according the Amadahl’s law which is
a model for the relationship between the expected
speedup of parallelized implementations of an algo-
rithm relative to the sequential algorithm.
The application is distributed over different pro-
cessors as defined. Master process is mapped as one
processor and farmer processes are mapped on the re-
maining processors. Each worker process executes
the same processing code on the different data. In
other words, the master process generates a sequence
of inputs (particles) and assigns each of them to one of
several slaves. Each worker handles one particle at a
time t, and it does this in parallel to all the other work-
ers which produces a sequence of outputs(weights).
The proposed algorithm is executed in N proces-
sors. Since M particles are generated and because
the processing time is regular, each worker eventu-
ally process M/N sample. Each processor calculates
the weights measurements for one sample, includ-
ing three measurements from face model, Kullback-
Leibler distance and weight importance. One can see
in figure 7 the parallel tracking algorithm scheme us-
ing Farm skeleton. Finally, the sample weights from
all processors are collected and the sample parame-
ter with maximum weight is selected to be the final
estimation for the target face. Resampling requires
knowledge of sum of all particle weights. Hence it
cannot begin before the weights of all the particles
have been calculated.
Figure 8 shows the whole application steps of the
face detection and tracking methods (including the
automatic skin detection step) of the FPGA imple-
mentation. The skin detection is delivered sequen-
tially by the master processor. The advantage of the
hardware implementation of this type of detector is
that it entails very small amounts of memory (mainly
the 128 bytes for the BRAM) and it gives sensible re-
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
130
Input
Image
Slave1 Slave2
Slave3
Master
Output
Image
Receive Receive
Receive
Send_Slave
Send_Slave
Send_Slave
Send
Send
Send
Model
Calculation
Model
Calculation
Model
Calculation
Dkl
Calculation
Dkl
Calculation
Dkl
Calculation
Weight
Calculation
Weight
Calculation
Weight
Calculation
Figure 7: Parallel face tracking using FARM (case of HNCP
with 4 processors).
Skin
Detection
Face
Tracking
Resampling
Video
Frame
Tracking
Window
Figure 8: FPGA face detection and tracking implementaion.
sults with a much lower computational cost. As seen
earlier, we compute the importance weights of M im-
age regions in parallel in order to identify the region
corresponding to the face in the current frame. As we
already mentioned, the determination of the resam-
pled set of particles is done sequentially due to data
dependencies among the particle during this step of
the algorithm.
5 EXPERIMENT
IMPLEMENTATION AND
COMPARISON
The experimental section is divided into two parts.
First, we perform experiments demonstrating the
properties of our tracking approach and second we
present results on public available sequences for com-
parison to other tracking approaches.
Given a video sequence centered around the hu-
man figure, each tracking task has been initialized by
manually marking the target object in the first frame.
The performance (speed) depends on the size of the
search region which we have defined by enlarging the
target region by one third in each direction (the model
representations of all the particles are generated in-
side this region). In our experiments color and motion
model has been used.
5.1 Results
In this section, we present the results of the imple-
mentation and a comparison of the proposed architec-
tures instantiated using CubeGen tool.
5.1.1 Sequential Implementation
We aim to demonstrate and evaluate the implementa-
tion of the proposed algorithm by tracking through
video-sequence of a human-centered environment.
The timing performances of the tracking algorithm
were measured by processing an input image of size
384*288 pixels.
Figure 9: Human face tracking.
For implementation of particle filter, M samples
randomly generated consisting of rectangular regions
are taken from the input image (Figure 9). So each
particle m carries information of {x
m
t
, y
m
t
} subwindow
coordinates m = 0...M and a weight between the tar-
get color window in the current frame and the ref-
erence color window. The color window with the
maximum weight s
max
t
is chosen as best candidate
for the face. In our experiments under sequential
mode, the number of search window (particles) is
set to 100 in order to be better concentrated around
the true state. The size of the search window (face)
H
Particle
xW
Particle
varies among different video se-
quence. We made several experiments on sequential
implementation. All this experiments have been done
on a standard 3 GHz PC with 3 GB RAM. Table 1
shows the execution time required for each process-
ing step of the algorithm and the number of search
windows used. The execution time is the time it takes
for processing a single frame. For the sequential im-
plementation on FPGA platform, Table 2 shows the
statistics of proposed face detection and tracking al-
gorithm on one MicroBlaze as soft-processor in our
network.
Hence, the parallel implementation of the devel-
oped resampling algorithm is vital to the development
of faster and more efficient real-time particle filters.
5.1.2 Parallel Implementation
We would like to make a comparison in terms of num-
ber of particles and the speedup. In order to investi-
FAST PROTOTYPING OF EMBEDDED IMAGE PROCESSING APPLICATION ON HOMOGENOUS SYSTEM - A
Parallel Particle Filter Tracking Method on Homogeneous Network of Communicating Processors (HNCP)
131
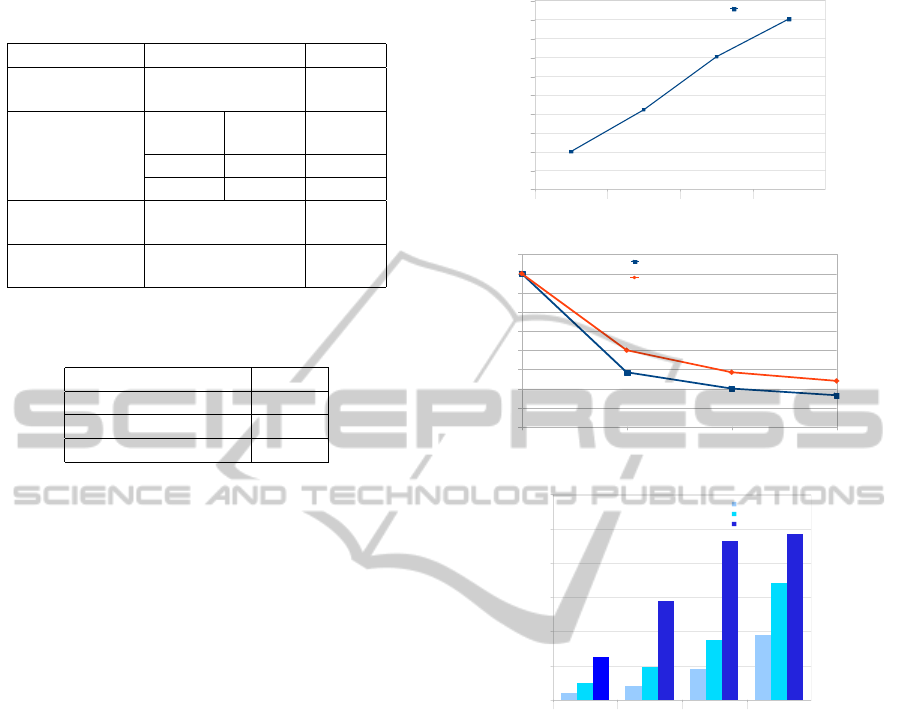
Table 1: Timing results /OS Windows XP 32 bits (384*288
pixels).
Samples 100 50
Time of
detection
3.6ms 3.6ms
Time(each
sample)
Generate
Sample
10µs 10µs
Model 140µs 140µs
Weight 445µs 445µs
Time of
tracking
65ms 35ms
Time of
resampling
180µs 180µs
Table 2: Timing results /HNCP with 1 processor(256*192
pixels).
Samples 15
Time of detection 8.7ms
Time of tracking 150ms
Time of Resampling 4.4ms
gate the performance with different sizes of network,
we set the particle number to 45 particle and the com-
puting core from 1 to 16 (dimension of HNCP D=1...4
i.e. 2
D
nodes). One can often expect and frequently
achieve an improvement in performance by using far
more particles. The performance figure is shown in
figure 10. The computing result is from one person
(one face) in the investigate frame. In each exper-
iment, we vary the number of particles evaluations
that can be processed in real-time with different sizes
of HNCP. We have taken the following measures to
show the variation caused by using different particle
number.
The performance of the proposed resampling al-
gorithms is rarely close to the theroretical speedup.
This can be seen from figure 11. The time of latency
in the developed algorithm depends on the number of
particles M.
Figure 12 summarizes the total utilization of the
proposed architectures. The entire SIR along with
the computational units of sampling and importance
was implemented on Xilinx Virtex 6 XC6VLX240T
board.
5.2 Results Analysis
Our results show that it is possible to achieve
real-time tracking even operating at relatively low
clock frequencies (using the platform XC6VLX240T-
1FFG1156 FPGA running at 200 MHz). From fig-
ure 11, we can observe that effectively the number of
particle M increases with the size of HNCP architec-
ture. There is significant gain in increasing the level
HNCP(1)
HNCP(4)
HNCP(8)
HNCP(16)
0
5
10
15
20
25
30
35
40
45
50
Nbre of particle
Figure 10: FPGA particle number.
HNCP(1)
HNCP(4)
HNCP(8)
HNCP(16)
0
20
40
60
80
100
120
140
160
180
theoretical
processing
time(ms)
processing time
obtained (ms)
Figure 11: FPGA processing time results.
HNCP (1 ) HNCP (4 ) HNCP (8 ) HNCP (16 )
0
0,2
0,4
0,6
0,8
1
1,2
Register
LUT
Block memory
Estimated Utilization %
Figure 12: FPGA Resource utilization of target device (Xil-
inx xc6v2x240tff 1156-1).
of parallelism when M/N becomes small. As can be
seen from the timing figure, the resampling step is a
bottleneck in the SIRF execution as it cannot be paral-
lelizable with other operations. Regarding the compu-
tation times, it should be mentioned that the proposed
tracking algorithm requires more than 93% of the to-
tal execution time according to the table 2 without the
resampling and the detection steps.
The time of resampling(including the time needed
to select the location of target as a particle with max-
imum weight) use less than 7% of the execution time
so does not significantly affect the total time of ex-
ecution with respect to the table 2. Consequently, it
is possible to implement the major bottleneck of the
algorithm (the computation of the color histograms
and, the particle weights) in a parallel manner suit-
able for our HNCP architecture, but also that the non-
parallelizable steps can be implemented efficiently.
The experimental results demonstrate that the parallel
Farm scheme can achieve a good speedup compared
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
132

to the corresponding sequentiel algorithms. Further-
more, as resampling is applied at every iteration of
the proposed algorithm, this can evaluating previous
particle weights. The final goal of this parallel imple-
mentation is to develop algorithms and architectures
that can reach the minimum execution time.
6 CONCLUSIONS
In this work, we have designed and implemented
a preliminary real time particle filter algorithm that
makes use of our MP-SOC architecture (HNCP) to
execute the algorithms main performance bottleneck.
Our strategy uses specific communication functions
based on our Parallel skeleton library for reducing
the computational efforts generated by the sequential
evaluation (Particle weights computation). Our ex-
periments on different video sequences showed that
search of Region of Interest (ROI) are accelerated
in order to achieve real-time tracking with relatively
small number of particles. The experiment results
show that the method can get a good effect and
speedup. This allows us to propose a particle filter
framwork for fast face tracking to achieve real time
performance using our HNCP architecture. As fu-
ture work, the research goal concerns the algorithm
implementation in a manner suitable for an FPGA-
based intelligent camera. In particular, we aim to
develop a robust self-localization approach for mo-
bile robot equipped with our architecture of a smart
camera based on Xilinx FPGA (camera with sensors
for high resolution image acquisition equipped with
HNCP architecture). Therefore, it seems important
to find a properly way to report results of applying
particle filters to providing a mobile robot with au-
tonomous capabilities.
REFERENCES
Anastasios, D. and Nikolaos, M. (2012). Visual under-
standing industrial workflows under uncertainty on
distributed service oriented architectures. Journal of
Original Research Article Future Generation Com-
puter Systems, 28:605–617.
Boli´c, M. (2004). Architectures for efficient implementation
of particle filters. PhD thesis, Stony Brook University,
New York.
Boli´c, M., Athalye, A., Djuric, P., and Hong, S. (2004).
Algorithmic modification of particle filter for hard-
ware implementation. In Proceedings of the European
Signal Processing Conference(EUSIPROC), Vienna,
Austria.
Boltz, S., Debreuve,
´
Eric., and Barlaud, M. (2009). High-
dimensional statistical measure for region-of-interest
tracking. IEEE Transactions on Image Processing,
18:1266–1283.
Chen, Z. (2003). Bayesian filtering: From kalman filters to
particle filters, and beyond. Statistics, pages 1–69.
Crisan, D., Del Moral, P., and Lyons, T. (1999). Discrete
filtering using branching and interacting particle sys-
tems. Journal of Markov Process and Related Fileds,
5(3):293–318.
De Bruijne, M. and Nielsen, M. (2004). Image segmen-
tation by shape particle filtering. In Proceedings of
the Pattern Recognition, 17th International Confer-
ence on (ICPR’04) Volume 3 - Volume 03, ICPR 04,
pages 722–725, Washington, DC, USA. IEEE Com-
puter Society.
Diaconis, P. (2003). Sequential monte carlo methods in
practice. Journal of the American Statistical Associa-
tion, 98:496–497.
Greg, W. and Gary, B. (1995). An introduction to the
kalman filter. Technical report, Chapel Hill, NC, USA.
Johncy Rani, T. and Suja Priyadharsini, S. (2010). Region
of interest tracking in video sequences. International
Journal of Computer Applications, 3(7):32–36.
Liu, K., Zhang, T., and Wang, L. (2010). A new par-
allel video understanding and retrieval system. In
ICME’10, pages 679–684.
Maskell, S. and Gordon, N. (2001). A tutorial on parti-
cle filters for on-line nonlinear/non-gaussian bayesian
tracking. Journal of IEEE Transactions on Signal Pro-
cessing, 50:174–188.
Medeiros, H., Park, J., and Kak, A. (2008). A parallel im-
plementation of the color-based particle filter for ob-
ject tracking. In IEEE Computer Society Conference
on Computer Vision and Pattern Recognition Work-
shops, pages 1–8, Anchorage, AK.
Petrovskaya, A. and Thrun, S. (2009). Model based vehicle
detection and tracking for autonomous urban driving.
Journal of Autonomous Robots, 26(2–3):123–139.
Poldner, M. and Kuchen, H. (2008). On implement-
ing the farm skeleton. Parallel Processing Letters,
18(1):117–131.
Si´eler, L., D´erutin, J., Damez, L., and Landrault, A. (2010).
A generic mp-soc design methodology for the fast
prototyping of embedded image processing. In Inter-
national Conference in Microelectronics (ICM), pages
104–107, Cairo. IEEE Computer Society.
Vezhnevets, V., Sazonov, V., and Andreeva, A. (2003). A
survey on pixel-based skin color detection techniques.
In PROC. GRAPHICON-2003, pages 85–92.
Xinyu, X. and Baoxin, L. (2005). Rao-blackwellised parti-
cle filter for tracking with application in visual surveil-
lance. In Proceedings of the 14th International Con-
ference on Computer Communications and Networks,
pages 17–24, Los Alamitos, CA, USA. IEEE Com-
puter Society.
FAST PROTOTYPING OF EMBEDDED IMAGE PROCESSING APPLICATION ON HOMOGENOUS SYSTEM - A
Parallel Particle Filter Tracking Method on Homogeneous Network of Communicating Processors (HNCP)
133
