RADIAL EDGE SPLATTING FOR VISUALIZING DYNAMIC

DIRECTED GRAPHS

Michael Burch

, Fabian Beck

and Daniel Weiskopf

VISUS, University of Stuttgart, Stuttgart, Germany

University of Trier, Trier, Germany

Keywords:

Graph Visualization, Node-link Diagrams, Radial Layout, Splatting.

Abstract:

We describe and discuss a novel radial version of a scalable dynamic graph visualization. The radial layout

encodes dynamic directed graphs on narrow rings of a circle. The temporal evolution of the graph is mapped to

rings that grow outward from the center of the circle. Graph vertices are placed equidistantly at the borderlines

of each ring. Graph edges are displayed as curved lines starting from a source on the inner borderline of the

ring and pointing to a target on the outer borderline. To better perceive link directions and structures of large

datasets, visual clutter is reduced by exploiting an edge splatting approach that generates density ﬁelds of the

displayed edges. The radial layout emphasizes newer graphs, displayed in the larger, outer parts of the circle.

As a beneﬁt, edge lengths are reduced in comparison to the non-radial visualization. Moreover, the radial

layout guarantees the symmetry of the visualization under shifting of vertices. We illustrate the usefulness of

the diagrams by applying them to call graph data of the open source software project Cobertura.

1 INTRODUCTION

Dynamic graph data occurs in various areas of appli-

cation. For example, social networks express relation-

ships among people. Those networks may evolve over

time, i.e., new people come into the network or rela-

tionships change. In another example, distances be-

tween elements of dynamic systems can be modeled

as dense graph structures and also these may change

over time. In the area of software development, call

graphs changing from release to release show which

software constructs call each other.

Those graph datasets are often too large for a man-

ual exploration of the raw data. When we have a clear

and speciﬁc question, we may apply algorithmic ap-

proaches. But in many applications, neither we know

such a question beforehand nor the problem can be re-

duced to a single question—some kind of visual rep-

resentation of this dynamic data is required that helps

us efﬁciently explore the dataset.

Creating such a visualization of dynamic directed

and weighted graphs is challenging due to the many

visual dimensions to be represented in a scalable way:

First of all, many nodes could be part of the graph.

Moreover, the graph could be dense; in other words,

many edges connect the nodes of the graph. Fi-

nally, the graph may evolve in a signiﬁcant number

of changes over a long period of time.

Animation can be used to visualize the dynamic

changes in a node-link diagram (Diehl and G

org,

2002; Frishman and Tal, 2008). However, animation

largely fails to provide an overview of the time dimen-

sion of the dataset; the cognitive issues of animated

visualization are discussed by (Tversky et al., 2002).

A better overview is provided if the time dimension

is mapped onto a (spatial) time line and the dynamic

graph is visualized in a single static image. Such

an approach that particularly focuses on the scalable

representation of dynamic graphs was presented by

(Burch et al., 2011b). It displays snapshots of the dy-

namic graph side-by-side in narrow vertical stripes.

Techniques like arranging the nodes onto parallel axes

and applying edge splatting (representing edges in a

density ﬁeld) are used to increase the scalability of

the single graph diagrams.

In our work, we introduce a radial version of par-

allel edge splatting (Burch et al., 2011b) to represent

dynamic directed and weighted graphs. The radial

layout shows the following beneﬁcial characteristics:

• It avoids long links pointing from the top to ver-

tices at the bottom and guarantees the symmetry

of the visualization if vertices are shifted.

• It puts emphasis on newer graphs displayed at

outer parts of the representation.

After discussing related work, we present the vi-

sualization technique in detail. The implemented vi-

sualization tool supports several interactive features

603

Burch M., Beck F. and Weiskopf D..

RADIAL EDGE SPLATTING FOR VISUALIZING DYNAMIC DIRECTED GRAPHS.

DOI: 10.5220/0003828506030612

In Proceedings of the International Conference on Computer Graphics Theory and Applications (IVAPP-2012), pages 603-612

ISBN: 978-989-8565-02-0

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

such as ﬁltering functions, aggregations in both time

and vertex dimensions, and details-on-demand. We

demonstrate the usefulness and the aesthetics of the

radial diagrams by applying it to call graph data from

the open source software project Cobertura. Finally,

we discuss the beneﬁts and drawbacks of the radial

visualization in comparison to its non-radial counter-

part.

2 RELATED WORK

Graphs are usually visualized as nodes connected by

graphical links. If not carefully laid out, visual clut-

ter, often caused by many link crossings, makes the

diagram hard to read. While (Rosenholtz et al., 2005)

provide a measure for such visual clutter, (Purchase

et al., 1996; Purchase et al., 2001; Purchase et al.,

2002) evaluate aesthetic criteria for node-link dia-

grams. The minimization of link crossings is ranked

very high, but also the maximization of symmetries

and the maximization of angles at crossing points is

of interest for good layout strategies. (Beck et al.,

2009) discuss a set of aesthetic criteria extended for

designing dynamic graph visualizations.

Animated node-link diagrams represent dynamic

graphs (Diehl and G

org, 2002; Frishman and Tal,

2008): A node-link diagram is shown to the viewer

and is then smoothly animated and transformed into

the next diagram. The layout algorithms try to keep

the layout of the graph as stable as possible while con-

currently presenting a readable layout in each single

diagram. By doing this, cognitive efforts are reduced

and the mental map of the viewer is preserved (Misue

et al., 1995).

In general, layout algorithms for node-link di-

agrams can be very complex and time-consuming.

Even elaborate approaches fail to produce nice lay-

outs for large graphs due to many link crossings. The

situation is even worse if a graph is not static but

changes in an animation. While changes in one step

can be observed by the user, animation cannot pro-

vide an overview of the time dimension. These prob-

lems led to the development of dynamic graph visual-

ization that shows the graph—including its temporal

changes—in a single static image.

A simple idea is to represent snapshots of the dy-

namically changing graph side-by-side on a time axis.

Doing this leads to a better overview with respect to

time but introduces also new problems like the much

smaller screen space assigned to each diagram and the

difﬁculty in tracking particular nodes across the se-

quence of diagrams. (Greilich et al., 2009) proposed

a tool called TimeArcTrees, where the vertices are pl-

aced on 1D vertical lines so that it is easy to track

the nodes. Edges are drawn as curved arcs. Al-

though an advanced layout is used for these arcs,

the visualization quickly becomes cluttered for dense

graphs. A more scalable approach applies an edge

splatting technique to compute density ﬁelds for the

graph edges (Burch et al., 2011b). The visualization

approach presented in this paper is a radial version of

the technique by (Burch et al., 2011b).

An alternative solution for representing a dy-

namic graph in a single image is the radial Time-

RadarTrees visualization technique (Burch and Diehl,

2008), where no edge crossings occur at all. Snap-

shots are still shown side-by-side, but matrix-like

representations and color coding are used to depict

graph edges. In the layered TimeRadarTrees ap-

proach (Burch et al., 2011a), this idea is enhanced to

obtain a scalable version of the visualization.

Recently, matrices have been used to depict a dy-

namic graph in a static image where edges are repre-

sented as colored cells of a matrix (Brandes and Nick,

2011; Gove et al., 2011; Stein et al., 2010; Yi et al.,

2010). For instance, (Stein et al., 2010) split each cell

of the matrix into subcells and use these to depict the

changing edge weights on a folded time line. (Bran-

des and Nick, 2011) follow a similar approach relying

on a different, yet more elaborate representation of

dynamic information in the cells of the matrix. The

main advantage of adjacency matrices is that they can

easily handle dense graphs. When using the cells of

the matrix to represent the dynamic information, each

cell, however, requires a signiﬁcant amount of screen

space, which leads to a decreased scalability with re-

spect to the number of nodes.

There are further approaches to represent dynamic

relational data that are, among other graph visual-

ization techniques, surveyed by (von Landesberger

et al., 2011). A survey of radial visualizations is

provided by (Draper et al., 2009). The evaluation

paper by (Diehl et al., 2010) analyzes strengths and

weaknesses of radial representations. It was found

out that non-radial representations outperformed ra-

dial ones with respect to memorizing positions of col-

ored boxes. We adopt the discussion of radial vs. non-

radial visualizations in Section 5, focusing on the par-

ticular cases of edge splatting of graph data.

3 VISUALIZATION TECHNIQUE

We introduce a novel visualization technique for dis-

playing dynamic directed and weighted graphs in a

single static diagram. We exploit the node-link visual

metaphor and map the graph vertices equidistantly to

IVAPP 2012 - International Conference on Information Visualization Theory and Applications

604

(a) (b) (c)

Figure 1: Visual encoding of graph data as node-link layouts: (a) Traditional 2D layout. (b) Mapping the vertices equidistantly

to vertical parallel axes in the same order and drawing the direct links inside the resulting narrow stripe as proposed by (Burch

et al., 2011b). (c) Drawing the vertices equidistantly along the borderlines of an annulus in the same order and representing

the edges as curved links pointing from the inside to the outside.

circular rings and edges as curved lines inside the nar-

row annuli (circle rings) pointing from an inner to

an outer annulus. For better visual perception of the

many edges in cluttered regions, we use an edge splat-

ting technique to derive density ﬁelds and to allow

users to explore edge directions and structures.

3.1 Data Model

In the context of this work, we model a directed and

weighted graph in the graph-theoretic sense as

G = (V, E)

where V denotes the set of vertices and E ⊆ V × V

the set of directed edges. Each edge e ∈ E is attached

with a weight w

A dynamic graph of length n is a sequence of n

single graphs and can be modeled as

G := (G

, . . . , G

)

where G

= (V

, E

), 1 ≤ i ≤ n.

3.2 Single Graph Representation

Typically, node-link graph diagrams are laid out in

the 2D plane, following several aesthetic criteria for

graph drawing such as minimization of link crossings,

maximization of angles at intersections, or maximiza-

tion of symmetries if those exist in a graph. Since

our focus is on dynamic graph visualization by static

diagrams, we need a more compact representation

that supports exploring and comparing a number of

graphs in a side-by-side view to easily uncover trends

and countertrends. We employ a visual mapping of

the graph vertices equidistantly to 1D vertical paral-

lel lines as demonstrated in the work of (Burch et al.,

2011b), a concept that is similar to parallel-coordinate

plots (Inselberg and Dimsdale, 1990). In the follow-

ing, we demonstrate how a single directed graph is

represented as a traditional 2D drawing, as a Cartesian

1D drawing as in the work of (Burch et al., 2011b),

and as a novel radial 1D drawing; see Figures 1 (a),

(b), and (c).

In Figure 1 (a), one graph with ﬁve vertices and

ﬁve edges is displayed by applying a graph layout al-

gorithm that generates a planar drawing in this case.

In Figure 1 (b), the graph vertices are mapped equidis-

tantly to a vertical axis. The vertex set is copied and

mapped in the same order to a second parallel verti-

cal axis. The directed graph edges are displayed in-

side the resulting narrow stripe, starting at the vertical

node position on the left axis and heading to the verti-

cal position of its target vertex on the axis at the right

hand side. Please note that arrow heads indicate the

direction of the links in the ﬁgures. The arrow heads

are for illustration purposes only and will be left out

in the actual graph visualizations.

In Figure 1 (c), the novel radial technique is il-

lustrated. To transform the Cartesian diagram into

a radial one, we connect the endpoints of the nar-

row stripe and obtain an annulus representation with

the links in between pointing from the inner border

to the outer border of the annulus. To prevent links

from leaving the annulus region, we transform the

straight links of the Cartesian diagram into curved

links, approximated by piecewise linear polygonal

curves. Such a curve is speciﬁed by the sequence of

n + 1 points

P := (P

, P

, . . . , P

)

where



i · (r

− r

)





cos(ϑ +

iϕ

)

sin(ϑ +

iϕ

)



and 0 ≤ i ≤ n.

The parameter r

is the radius of the inner border

of the annulus and r

the radius of the outer border of

RADIAL EDGE SPLATTING FOR VISUALIZING DYNAMIC DIRECTED GRAPHS

605

(a) (b)

Figure 2: Mapping of a single directed graph edge: (a) Left

to right mapping between two vertical parallel axes as a

straight link. (b) Mapping to an annulus from the inside

to the outside as a curved link.

the annulus. The angle ϑ is the angular position of the

start vertex, whereas ϕ is the angle that is needed to

point to the target vertex, i.e., the shifting angle.

The mapping of a single edge to a straight and a

curved line is illustrated in Figures 2 (a) and (b), re-

spectively. In Figure 2 (a), a directed edge leads from

node v

to another node v

among m nodes v

, . . . , v

The start vertex is displayed on the left axis and the

target vertex is displayed at the corresponding posi-

tion on the right axis. The directed edge is indicated

by a red colored straight line between the two corre-

sponding nodes. In the radial representation in Fig-

ure 2 (b), the same edge is shown. Now, the vertices

are mapped to the borderlines of the annulus and the

edge is displayed as a curved link running from the

inside to the outside.

Figures 3 (a) and (b) demonstrate how long links

in the Cartesian diagram are shortened by using a ra-

dial representation. In Figure 3 (a), a straight link

points from node v

to node v

. This link crosses a

large part of the display in a diagonal fashion and has

a high probability to lead to link crossings. In the

radial representation like illustrated in Figure 3 (b),

there are two possibilities to render the curved link.

Our edge layout algorithm minimizes link lengths by

always picking the shorter of the two options. Hence,

the dashed link in Figure 3 (b) will be avoided.

3.3 Dynamic Graph Representation

For representing a dynamic directed graph, we fol-

low the same principle as for the Cartesian diagram

of (Burch et al., 2011b). In their work, all graphs

are mapped to subsequent narrow stripes from left to

right. In our work, we map each graph to an annulus

and the whole graph sequence to many annuli starting

in the circle center with the oldest graph and ending

with the newest graph at the outside. By doing this,

we put emphasis on newer graphs by mapping them

to a larger display space, which is an intuitive concept

ϑ'

ϕ'

(a) (b)

Figure 3: Reduction of link length by switching the orienta-

tion: (a) A directed straight link crossing a large part of the

display. (b) A mapping to an annulus representation allows

two possible directions of the curved link—clockwise and

counter clockwise. Our edge layout algorithm minimizes

link length by picking the shorter of the two potential links.

Hence, it avoids the dashed link as illustrated.

for time-series data visualization.

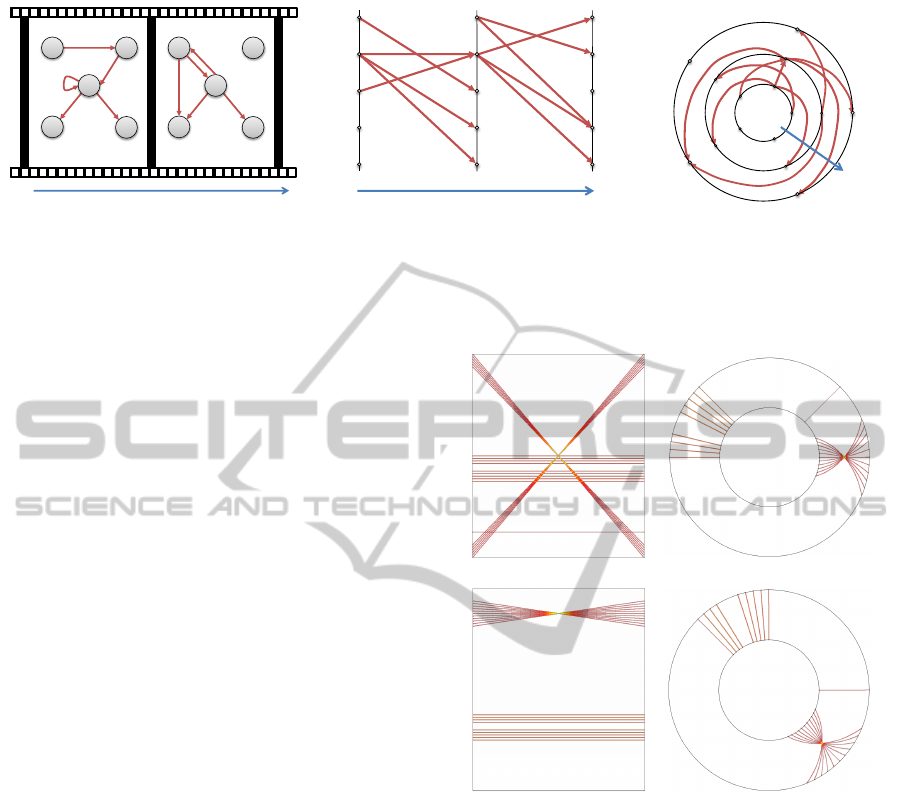
Figures 4 (a), (b), and (c) demonstrate how a se-

quence of two directed graphs is visualized as an

animated node-link diagram (a), as a 1D node-link

representation to parallel vertical axes (b), and as a

sequence of annuli with curved links pointing from

the inside to the outside (c). Please note that we do

not distinguish between removed vertices and vertices

that are not adjacent to any other vertex.

3.4 Edge Splatting

A negative consequence of node-link diagrams is the

occurrence of visual clutter caused by many link

crossings. By mapping the graph to 1D vertical axes

and the edges as straight or curved links in between,

we gain a lot of space to display the dynamics of the

graph on the positive side, but we also increase the

problem of visual clutter on the negative side.

To alleviate the problem, we apply the concept of

edge splatting as it is also used in the work of (Burch

et al., 2011b). By computing density ﬁelds for the

edges, the link directions and structures become visi-

ble again.

3.5 Beneﬁts of Radial Edge Routing

The technique has the beneﬁt that formerly long links

become shorter by only allowing a maximal link

length l ∈ [r

· π, r

· π] where r

and r

are the radii

of the inner and outer borders of the respective annu-

lus. In our case we use a curved link representation

style that exactly generates links of length π ·

Figure 5 (a) and (b) illustrate the minimization of link

length for an example dataset. In Figure 5 (a), there is

an X-pattern leading to visual clutter caused by cross-

ings with the parallel horizontal lines, which is re-

IVAPP 2012 - International Conference on Information Visualization Theory and Applications

606

time (animation)

time

(a) (b) (c)

Figure 4: A sequence of two directed graphs can be represented in different styles: (a) Animated node-link diagrams. (b)

Sequence of node-link diagrams mapped to 1D parallel vertical axes. (c) Sequence of annuli starting in the circle center and

ending with the newest graph at the outside.

solved in Figure 5 (b) by just connecting the upper

and lower endpoints of the Cartesian representation.

The radial version transforms the ﬁnite and bounded

vertical axes of the Cartesian diagram to cyclic annuli

(i.e., without bounding the angle position of vertices).

Another consequence of routing the edges in a ra-

dial fashion is that the visualization becomes invari-

ant under shifting of vertices. In Figure 5 (c) and (d)

we shifted the vertex positions of Figure 5 (a) and

(b) by 10 positions. In the Cartesian version, this

results in a visualization that looks signiﬁcantly dif-

ferent from the original non-shifted version because

the vertices that created the dominating X-pattern are

no longer split by the borders of the stripe. In con-

trast, the shifted radial visualization only changes

marginally—it is only rotated by a small angle.

3.6 Interactive Features

Since we follow the Visual Information Seeking

Mantra introduced by (Shneiderman, 1996), we ﬁrst

generate an overview representation of the graph se-

quence that serves as a starting point for an explo-

ration process. Apart from the static overview, the vi-

sualization supports the following interactive features

such as aggregation in the vertex and time dimension

and several ﬁltering functions. Also graph-speciﬁc

tasks such as shortest path detection can be solved

algorithmically and their evolution over time can be

displayed visually.

• Selection of Time Intervals. Representing many

timesteps results in very narrow radial annuli and

consequently, each graph of a displayed sequence

is difﬁcult to interpret. For this reason, the user is

supported by selecting a speciﬁc time interval and

only the graphs which belong to this interval are

represented.

• Graph Aggregation. In many cases, a stability

pattern occurs in the graph sequence, i.e., there are

(a) (b)

Figure 5: Beneﬁcial characteristics of radial edge routing:

(a) Cartesian representation with links crossing the whole

display. (b) The radial version with shorter links. (c) A

shifted Cartesian visualization, which results in major vi-

sual changes. (d) The equivalent shifted radial visualization,

which only results in minor visual changes.

only a few changes between subsequent graphs.

It makes sense to aggregate all those graphs to

have more display space for graphs that frequently

change.

• Vertex Aggregation. Neighbored vertices can be

aggregated to also increase scalability in the ver-

tex dimension. If a hierarchical organization of

the vertices exists, this can be used to collapse or

expand vertex groups.

• Edge Weight Filtering. Edges can be ﬁltered by

selecting a weight interval. Only those edges with

RADIAL EDGE SPLATTING FOR VISUALIZING DYNAMIC DIRECTED GRAPHS

607

a weight contained inside the deﬁned interval are

represented on screen. All the others are either

grayed out or not drawn on screen at all. Another

ﬁltering can be applied to the values of the edge

density ﬁeld generated by our edge splatting ap-

proach.

• Added and Removed Edges. We allow two ad-

ditional operations for the edges. Added and re-

moved relations between two subsequent graphs

in the sequence can be computed and only those

edges are displayed by the tool. This feature

helps to analyse the differences between subse-

quent graphs even if the graphs are very dense.

• Textual Search. The tool allows to search for

substrings in the set of descriptive informations

for the vertices, i.e., for substrings in labels.

• Path Tracking. By specifying a start and a target

vertex, the shortest path between these vertices is

computed and highlighted on screen in all of the

displayed graphs. This feature can be used to ob-

tain an overview about the evolution of a graph-

speciﬁc property.

• Color Coding. The tool supports different color

schemes that can be applied to the visualization.

By doing this, a viewer can analyze the data on

different levels of weight granularity.

• Details-on-Demand. We also support details-on-

demand to analyze the corresponding meta infor-

mation of the dataset, e.g., the timestamp, the re-

lease number, or the labeling information of the

vertices.

The tool supports many more interactive features that

cannot be mentioned all in this paper and many more

will be implemented in future.

4 CASE STUDY: CALL GRAPH

VISUALIZATION

In this case study, we want to illustrate how the tool

can be applied in practice. We decided to visualize the

method calls of a software project that change from

release to release. Such a graph does not only ex-

plain the design of a single version, but also how this

design evolves over the versions. Visualizing such

a dynamic graph, however, is challenging since al-

ready small software projects may consist of hundreds

or thousands of methods. We chose the open source

project Cobertura

as a comprehensive example to be

analyzed.

http://cobertura.sourceforge.net/

4.1 Cobertura

Cobertura is a software engineering tool for retrieving

the test coverage of Java programs. It instruments the

Java bytecode of the program, runs the test cases, and

ﬁnally generates a report on test coverage. Cobertura

itself is written in Java and released as open source.

In the latest analyzed version (version 1.9.4), it con-

sists of 99 classes and 18 packages. Since version 1.0

was released in 2005, 13 stable update releases have

followed quite regularly up to version 1.9.4.

We downloaded these 14 stable versions of Cober-

tura, analyzed the bytecode using the tool Dependen-

cyFinder

, and extracted the method call graph of the

project. This dynamic graph is described by a se-

quence of 14 graphs (versions of Cobertura). In to-

tal, the static graphs consist of 4,812 individual nodes

(methods) and 27,208 edges (method calls). Figure 6

(a) shows the call graph by radial edge splatting. To

highlight the changes in the graph, we also computed

the method calls that were added or removed be-

tween two consecutive versions. Figure 6 (b) depicts

the added method calls while Figure 6 (c) illustrates

which ones were removed.

4.2 Observations

A ﬁrst observation in Figure 6 (a) is that the project

in terms of the number of method calls is growing,

however, more stepwise than continuously. The two

steps that come along with the most signiﬁcant modi-

ﬁcations are version 1.8 and version 1.9.3. They refer

to the javancss package, which is ﬁrst introduced

in version 1.8 and heavily extended in version 1.9.3.

These abrupt modiﬁcations suggest that this package

was not developed stepwise as a part of the Cober-

tura project, but imported from somewhere else. A

web search conﬁrmed this assumption: javaNCSS

a command line tool for computing software metrics.

Different versions of javaNCSS seem to relate to the

observed changes.

An interesting information that the visualization

indicates is the similar visual pattern that repeatedly

appears in javaNCSS in versions 1.9.3 and 1.9.4 of

Cobertura. This pattern is repeated four times in both

versions, whereas two of the repetitions are smaller

than the other two. A detailed analysis revealed that

each of the repeated patterns is related to a Java parser.

There are four parsers integrated into javaNCSS be-

cause two versions of Java are supported and for both

versions also a debug parser exists. In version 1.8 up

to version 1.9.2 of Cobertura, there is only one parser

http://depﬁnd.sourceforge.net/

http://javancss.codehaus.org

IVAPP 2012 - International Conference on Information Visualization Theory and Applications

608

javancss

1.0

1.1

1.2

1.3

1.4

1.5

1.6

1.7

1.8

1.9

1.9.1

1.9.2

1.9.3

1.9.4

core

(a)

(b)

(c)

Figure 6: Visualizing the call graph of methods in Cobertura over different releases. (a) All method calls. (b) Added method

calls. (c) Removed method calls.

version, which creates a similar visual pattern. Al-

though this single pattern does not seem to change

signiﬁcantly, Figures 6 (b) and (c) reveal that there

were some signiﬁcant changes in version 1.9.1.

The rest of the system beside the javancss pack-

age is what we labeled as the core of Cobertura in Fig-

ure 6 (a). In contrast to javaNCSS, the development

takes place much more steadily in this part. While

in the ﬁrst three versions the graph structure is quite

volatile, it forms a stable corpus from version 1.4 on-

wards. However, still signiﬁcant changes are made in

the subsequent versions as the number of added edges

tell in Figure 6 (b). This development continues up

to version 1.9—the following versions seem to be in-

deed only minor releases as already indicated by the

version number.

5 DISCUSSION

Many visualization approaches are based on a radial

layout (Draper et al., 2009). But often, it would have

been possible to implement the same approach in a

non-radial fashion. Besides the often aesthetically

pleasing appearance of the radial visualizations, it is

not clear whether this design decision in favor of a

radial is also justiﬁed by increased readability.

For instance, pie charts are radial versions of bar

charts. While pie charts seem to be very popular

in practice, information visualization researchers of-

ten complain about their frequent usage. The effec-

tiveness of both types of diagrams was empirically

evaluated in comparative experiments (Cleveland and

McGill, 1986; Schonlau and Peters, 2008; Spence and

Lewandowsky, 1991). These experiments, however,

do not come to a consistent conclusion. Other types of

radial visualization approaches were also compared

to their non-radial counterparts (Andrews and Kasan-

icka, 2007; Burch et al., 2008; Kobsa, 2004; Stasko

et al., 2000). But it would be questionable to gener-

alize the results retrieved for those specialized visual-

izations and directly apply these to the visualization

presented in the current work.

(Diehl et al., 2010) compared radial and non-

radial layouts choosing a more generic visualization

and task. They analyzed how users are able to memo-

rize positions in radial and Cartesian (non-radial) co-

ordinate systems. The general trend was that users

made more mistakes and needed more time remem-

bering the positions in the radial visualizations. But

looking at the details of the study, there were also ad-

vantages of radial visualizations: Participants could

memorize circle sectors much better than circle rings,

and also than rows or columns in the Cartesian coor-

dinate system. In the following, we discuss the new

RADIAL EDGE SPLATTING FOR VISUALIZING DYNAMIC DIRECTED GRAPHS

609

(a)

(b)

Figure 7: Comparing the radial visualization to its Carte-

sian counterpart based on the Cobertura call graph: (a) The

radial diagram. (b) The Cartesian diagram.

radial visualization in the light of these empirical re-

sults and theoretical considerations.

Figure 7 compares our radial visualization (a) to

its Cartesian counterpart (b) following the approach

of (Burch et al., 2011b). Both parts show the Cober-

tura dataset presented in the case study. They serve as

an example for discussing the beneﬁts and drawbacks

of the radial version.

5.1 Traceability of Edges

The technique of our new visualization has the beneﬁt

that some formerly very long links become shorter be-

cause now there are two ways to come from a source

to a target: clockwise and counter-clockwise. The

edge routing algorithm chooses the shorter one as dis-

cussed in Section 3.5. This could have a signiﬁcant

impact on the visualizations: The example of Fig-

ure 7 (b) shows a quite dominating x-pattern consis-

tent over all versions of Cobertura, which, however, is

only a visual artifact. In contrast, the radial version in

Figure 7 (a) shows no such exaggerated artifact.

Moreover, in the radial visualization formerly

straight links become curved. Our ﬁrst subjective im-

pression was that these curved lines are harder to fol-

low. This could be related to the observation that the

positions of rings are hard to memorize (Diehl et al.,

2010) because, especially when learning the position

relative to another position, following circular lines

would be required. This research question is also re-

lated to whether curved links in node-link diagrams

are beneﬁcial in general—some empirical evidence

suggests that they are not (Holten et al., 2011). But

to ﬁnally judge whether the curved links are a draw-

back of the radial visualization, the impact of this ef-

fect needs to be empirically evaluated for our radial

visualization.

5.2 Space Efﬁciency

The radial visualization provides an inherent focus-

and-context mechanism. The outer rings of a ra-

dial layout cover more space than the inner rings.

This automatically focuses the outer graphs in the se-

quence of graphs, which are the newer ones when

the time line starts at the circle center. Depending

on the application, this can be a valuable beneﬁt: In

many applications we are interested most in the re-

cent development—the longer history just provides a

context. Analyzing the evolution of software projects

as demonstrated in the case study is an example for

that. In applications where the focus should not be

ﬁxed, inverting, rotating, or reordering the time line

may switch the focus appropriately. Nevertheless, de-

activating the inherent focus is not possible.

Comparing the single stripes (annuli) in the radial

visualization to the stripes of the Cartesian version,

the stripes are longer, but even narrower in the radial

version. Although it is not clear what the ideal aspect

ratio of these stripes should be, it seems that the radial

stripes might be too narrow. Hence, interactively fo-

cusing and enlarging a stripe is more important in the

radial visualization.

Computer screens usually have a rectangular for-

mat. This format better ﬁts a Cartesian coordinate

system. In a radial visualization some space in the

corners of the screen cannot be directly used by the

visualization. Nevertheless, often the spare screen

space can be used for displaying additional informa-

tion like a legend or some interactive controls.

5.3 Visual Patterns

Different visual patterns that could help to inter-

pret the visualization are discussed by (Burch et al.,

2011b). These patterns show also up in the radial ver-

sion of the visualization. But here, they are somewhat

harder to detect since they occur not only in scaled

IVAPP 2012 - International Conference on Information Visualization Theory and Applications

610

and transposed versions, but could also be rotated. An

advantage of the radial version, however, could be that

the direction of the edges is better expressed through

the growing size of the annuli—incoming edges can

only hardly be mistaken for outgoing edges.

Reordering the vertices may change the look of

the visual patterns signiﬁcantly, both in the radial as

well as in the Cartesian visualization. When, how-

ever, only shifting a set of vertices, the radial visual-

ization guarantees stable patterns among the shifted

vertices. In contrast, those patterns are obscured in

the Cartesian visualization when moving the set of

vertices across the upper or lower border of the di-

agram. The advantage of the radial diagram is that

those borders do not exist as each strip forms a ring

(Section 3.5).

6 CONCLUSIONS AND FUTURE

WORK

We have introduced and discussed a novel radial vi-

sualization technique for displaying dynamic directed

and weighted graphs in a static diagram. The visual-

ization is a radial version of the parallel edge splatting

approach (Burch et al., 2011b). It employs a 1D map-

ping of the graph vertices to circle circumferences.

The resulting annuli are used to draw the graph edges

from the inside to the outside in a curved style. To

support a viewer with the difﬁcult task of tracing links

in large and dense graph structures, the visualization

is based on the concept of edge splatting, which color

codes the edge density. We illustrate the usefulness of

the technique by applying it to a dataset of evolving

call graphs extracted from an open source software

project.

By using a radial representation, we achieve

shorter links than in the Cartesian counterpart; in ad-

dition, the visualization is invariant under shifting the

positions of all vertices, which is not the case in the

Cartesian counterpart. Furthermore, we put emphasis

on newer graphs in the evolution that are mapped to

the outer annuli covering more screen space. A major

drawback of the radial technique could be the curved

links that seem to be harder to follow.

Whether the advantages outweigh the drawbacks

of choosing a radial layout is not clear, but it proba-

bly depends on the particular application. Perform-

ing a thorough empirical study with different tasks

and datasets to evaluate this is part of possible fu-

ture work. Another unanswered question and a quite

challenging task is to generate an optimal vertex or-

dering with the goal to further reduce link crossings.

Since this belongs to the class of NP-hard problems

and is related to the optimal linear arrangement prob-

lem (Garey and Johnson, 1979), we would have to ap-

ply some heuristic approach to ﬁnd a good solution.

REFERENCES

Andrews, K. and Kasanicka, J. (2007). A Comparative

Study of Four Hierarchy Browsers Using the Hierar-

chical Visualisation Testing Environment (HVTE). In

Proceedings of International Conference on Informa-

tion Visualization (IV), pages 81–86. IEEE Computer

Society Press.

Beck, F., Burch, M., and Diehl, S. (2009). Towards an

Aesthetic Dimensions Framework for Dynamic Graph

Visualisations. In Proceedings of International Con-

ference on Information Visualization (IV), pages 592–

597. IEEE Computer Society Press.

Brandes, U. and Nick, B. (2011). Asymmetric Relations in

Longitudinal Social Networks. IEEE Transactions on

Visualization and Computer Graphics, 17(12):2283–

2290.

Burch, M., Bott, F., Beck, F., and Diehl, S. (2008). Carte-

sian vs. Radial — A Comparative Evaluation of Two

Visualization Tools. In Proceedings of International

Symposium on Visual Computing (ISVC), pages 151–

160.

Burch, M. and Diehl, S. (2008). TimeRadarTrees: Visualiz-

ing Dynamic Compound Digraphs. Computer Graph-

ics Forum, 27(3):823–830.

Burch, M., H

oferlin, M., and Weiskopf, D. (2011a). Lay-

ered TimeRadarTrees. In Proceedings of International

Conference on Information Visualization (IV), pages

18–25. IEEE Computer Society Press.

Burch, M., Vehlow, C., Beck, F., Diehl, S., and Weiskopf,

D. (2011b). Parallel Edge Splatting for Scalable Dy-

namic Graph Visualization. IEEE Transactions on

Visualization and Computer Graphics, 17(12):2344–

2353.

Cleveland, W. S. and McGill, R. (1986). An Experiment in

Graphical Perception. International Journal of Man-

Machine Studies, 25(5):491–501.

Diehl, S., Beck, F., and Burch, M. (2010). Uncovering

Strengths and Weaknesses of Radial Visualizations—

an Empirical Approach. IEEE Transactions on Visu-

alization and Computer Graphics, 16(6):935–942.

Diehl, S. and G

org, C. (2002). Graphs, They Are Changing.

In Proceedings of International Symposium on Graph

Drawing, pages 23–30. Springer.

Draper, G., Livnat, Y., and Riesenfeld, R. (2009). A Sur-

vey of Radial Methods for Information Visualization.

IEEE Transactions on Visualization and Computer

Graphics, 15(5):759–776.

Frishman, Y. and Tal, A. (2008). Online Dynamic Graph

Drawing. IEEE Transactions on Visualization and

Computer Graphics, 14(4):727–740.

Garey, M. R. and Johnson, D. S. (1979). Computers

and Intractability: A Guide to the Theory of NP-

RADIAL EDGE SPLATTING FOR VISUALIZING DYNAMIC DIRECTED GRAPHS

611

Completeness. W. H. Freeman & Co., New York, NY,

USA.

Gove, R., Gramsky, N., Kirby, R., Sefer, E., Sopan, A.,

Dunne, C., Shneiderman, B., and Taieb-Maimon, M.

(2011). NetVisia: Heat Map and Matrix Visualization

of Dynamic Social Network Statistics and Content. In

Proceedings of IEEE Conference on Social Comput-

ing. IEEE Press.

Greilich, M., Burch, M., and Diehl, S. (2009). Visualizing

the Evolution of Compound Digraphs with TimeArc-

Trees. Computer Graphics Forum, 28(3):975–982.

Holten, D., Isenberg, P., van Wijk, J. J., and Fekete, J.-D.

(2011). An Extended Evaluation of the Readability of

Tapered, Animated, and Textured Directed-Edge Rep-

resentations in Node-Link Graphs. In Proceedings of

the Paciﬁc Symposium on Visualization, pages 195–

202.

Inselberg, A. and Dimsdale, B. (1990). Parallel Coordi-

nates: A Tool for Visualizing Multi-Dimensional Ge-

ometry. In Proceedings of IEEE Visualization, pages

361–378.

Kobsa, A. (2004). User Experiments with Tree Visualiza-

tion Systems. In IEEE Symposium on Information Vi-

sualization, pages 9–16. IEEE Computer Society.

Misue, K., Eades, P., Lai, W., and Sugiyama, K. (1995).

Layout Adjustment and the Mental Map. Journal of

Visual Languages and Computing, 6(2):183–210.

Purchase, H. C., Carrington, D., and Allder, J.-A. (2002).

Empirical Evaluation of Aesthetics-Based Graph Lay-

out. Empirical Software Engineering, 7(3):233–255.

Purchase, H. C., Cohen, R. F., and James, M. (1996). Val-

idating Graph Drawing Aesthetics. In Proceedings of

International Symposium on Graph Drawing, pages

435–446.

Purchase, H. C., McGill, M., Colpoys, L., and Carrington,

D. (2001). Graph Drawing Aesthetics and the Com-

prehension of UML Class Diagrams: An Empirical

Study. In Proceedings of the Asia-Paciﬁc Symposium

on Information Visualisation, pages 129–137.

Rosenholtz, R., Li, Y., Mansﬁeld, J., and Jin, Z. (2005).

Feature Congestion: A Measure of Display Clutter. In

Proceedings of SIGCHI Conference on Human Fac-

tors in Computing Systems, pages 761–770.

Schonlau, M. and Peters, E. (2008). Graph Comprehension:

An Experiment in Displaying Data as Bar Charts, Pie

Charts and Tables With and Without the Gratuitous

3rd Dimension. Social Science Research Network

Working Paper Series.

Shneiderman, B. (1996). The Eyes Have It: A Task

by Data Type Taxonomy for Information Visualiza-

tions. In Proceedings of IEEE Symposium on Visual

Languages, pages 336–343. IEEE Computer Society

Press.

Spence, I. and Lewandowsky, S. (1991). Displaying Pro-

portions and Percentages. Cognitive Psychology,

5(1):61–77.

Stasko, J., Catrambone, R., Guzdial, M., and McDonald, K.

(2000). An Evaluation of Space-Filling Information

Visualizations for Depicting Hierarchical Structures.

International Journal of Human-Computer Studies,

53(5):663–694.

Stein, K., Wegener, R., and Schlieder, C. (2010). Pixel-

Oriented Visualization of Change in Social Networks.

In Proceedings of the International Conference on Ad-

vances in Social Networks Analysis and Mining, pages

233–240. IEEE Computer Society.

Tversky, B., Morrison, J. B., and B

etrancourt, M. (2002).

Animation: can it facilitate? International Journal on

Human-Computer Studies, 57(4):247–262.

von Landesberger, T., Kuijper, A., Schreck, T., Kohlham-

mer, J., van Wijk, J. J., Fekete, J.-D., and Fellner,

D. W. (2011). Visual Analysis of Large Graphs: State-

of-the-Art and Future Research Challenges. Computer

Graphics Forum, 30(6):1719–1749.

Yi, J. S., Elmqvist, N., and Lee, S. (2010). TimeMatrix: An-

alyzing Temporal Social Networks Using Interactive

Matrix-Based Visualizations. International Journal of

Human-Computer Interaction, 26(11):1031–1051.

IVAPP 2012 - International Conference on Information Visualization Theory and Applications

612