
PLANNING GRAPH HEURISTICS FOR SOLVING
CONTINGENT PLANNING PROBLEMS
Incheol Kim and Hyunsik Kim
Department of Computer Science, Kyonggi University, San94-6, Yiui-Dong, Suwon, Korea
Keywords: Contingent Planning, Belief State Space, Search Heuristic, Planning Graph.
Abstract: In order to extract domain-independent heuristics from the specification of a planning problem, it is
necessary to relax the given problem and then solve the relaxed one. In this paper, we present a new
planning graph, Merged Planning Graph(MPG), and GD heuristics for solving contingent planning
problems including both uncertainty about the initial state and non-deterministic action effects. MPG is a
new version of the relaxed planning graph for solving the contingent planning problems. In addition to the
traditional delete relaxations of deterministic actions, MPG makes the effect-merge relaxations of both
sensing and non-deterministic actions. Parallel to the forward expansion of MPG, the computation of GD
heuristics proceeds with analysis of interactions among goals and/or subgoals. GD heuristics estimate the
minimal reachability cost to achieve the given goal set by excluding redundant action costs. Through
experiments in several problem domains, we show that GD heuristics are more informative than the
traditional max and additive heuristics. Moreover, in comparison to the overlap heuristics, GD heuristics
require much less computational effort for extraction.
1 INTRODUCTION
Most of planning problems encountered in the real
world environments have some uncertainty in both
the initial state and action effects. We call it
contingent planning to generate plans with
conditional branching based on the outcomes of
sensing actions for such environments with partial
observability and non-determinism. A well-known
technique for finding a contingent plan is to search
over belief states (Bonet and Geffner, 2001).
However, the size of the belief space for a
contingent planning problem is exponentially larger
than that of the corresponding state space. Therefore,
in order to find a contingent plan in tractable time,
we need powerful heuristics to guide efficiently the
belief space search.
In order to extract domain-independent heuristics
from the specification of a planning problem, it is
necessary to relax the given problem and then solve
the relaxed one (Hoffmann and Brafman, 2005). In
this paper, we present a new planning graph, Merged
Planning Graph (MPG), and GD heuristics for
solving contingent planning problems. In addition to
the traditional delete relaxations of deterministic
actions, MPG makes the effect-merge relaxations of
both sensing and non-deterministic actions. Parallel
to the forward expansion of MPG, the computation
of GD heuristics proceeds with analysis of
interactions among goals and/or subgoals. GD
heuristics estimate the minimal reachability cost to
achieve the given goal set by excluding unnecessary
action costs. Through experiments, the performance
of our GD heuristics will be compared with those of
other existing heuristics.
2 CONTINGENT PLANNING
PROBLEMS
We assume to find effective heuristics for solving a
contingent planning problem, like the one in Figure
1. The example problem given in Figure 1 is from
the dinner domain, which includes one sensing
action, sense_garbage, and one non-deterministic
action, cook. We notice that both sense_garbage and
cook actions have multiple possible outcomes as
described in their action definitions. Figure 2 shows
a contingent plan as solution for the example
planning problem given in Figure 1. It contains
multiple branches, every of which ends with a belief
515
Kim I. and Kim H..
PLANNING GRAPH HEURISTICS FOR SOLVING CONTINGENT PLANNING PROBLEMS.
DOI: 10.5220/0003830505150519
In Proceedings of the 4th International Conference on Agents and Artificial Intelligence (ICAART-2012), pages 515-519
ISBN: 978-989-8425-95-9
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
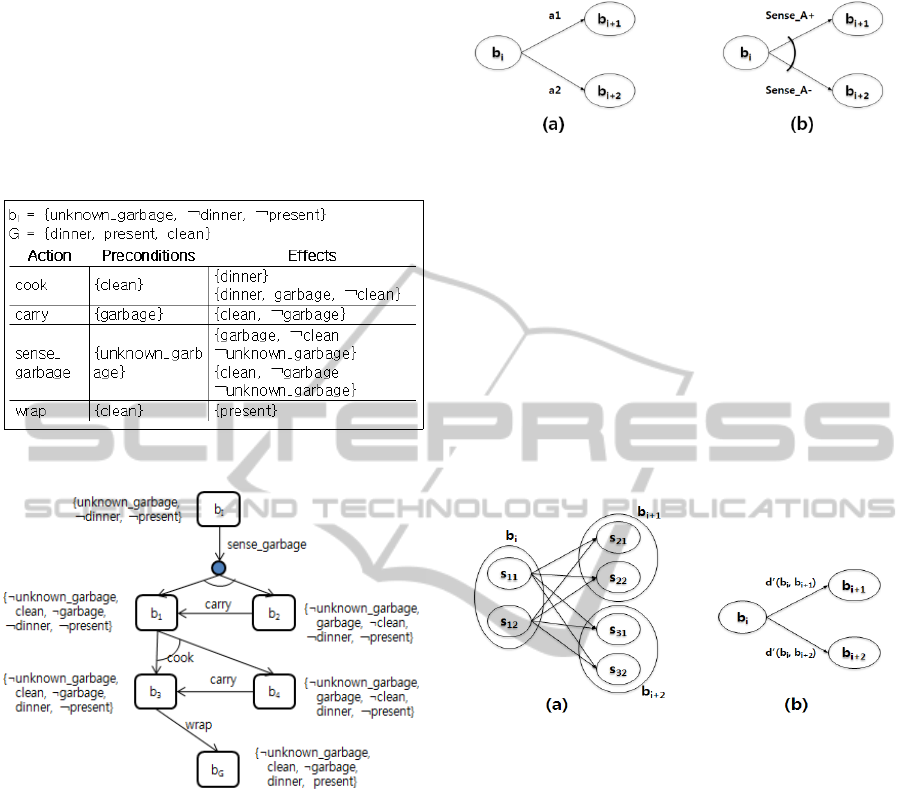
state satisfying all goal conditions. While the
occurrence of a sensing action during belief space
search generates more than one AND branch, in
general, the occurrence of a non-deterministic action
generates more than one OR branch. Through this
kind of AND-OR search on the belief state space,
we can find a contingent plan whose every AND
branch guarantees satisfaction of all goal conditions.
Figure 1: An example of contingent planning problem.
Figure 2: A contingent plan for the example problem
described in Figure 1.
3 HEURISTICS FOR BELIEF
SPACE SEARCH
Consider possible transitions from a belief state by
executing an action. As illustrated in Figure 3 (a),
execution of a deterministic action makes a
deterministic transition to a single belief state.
However, as shown in Figure 3 (b), execution of a
sensing or non-deterministic action makes a
transition to one of multiple different belief states. In
our work, we assume that a sensing action has only
two different effects.
In order to find a contingent plan from the belief
space search, a good distance-based heuristic is
needed. We should answer the questions of how to
Figure 3: Possible transitions on a belief space.
compute belief state distances and which measures
are most effective. Many approaches estimate belief
state distances in terms of individual state to state
distances between states in two belief states as
shown in Figure 4 (a). The distance between two
belief states in Figure 4 (b) can be estimated by
aggregating the individual state distances in Figure 4
(a). Existing approaches to estimating the belief state
distance are to select the maximal one from the
corresponding individual state distances (Max
heuristics), to sum all state distances (Additive
heuristics), or to add some part of state distances by
computing a relaxed plan (Overlap heuristics).
Figure 4: Estimating the distance between two belief states.
4 MERGED PLANNING GRAPH
The relaxed planning graph, which is an efficient
data structure used to compute search heuristics for
classical planning problems, is built from only
delete-relaxed deterministic actions. However, in
order to use the relaxed planning graphs for solving
contingent planning problems, additional relaxations
of sensing and non-deterministic actions are needed
(Bryce, et al., 2006). Recent some works (Bonet and
Geffner, 2005) tried to make effect-determinization
of non-deterministic actions, which splits a non-
deterministic action into multiple deterministic
actions. In this paper, we propose a new kind of
relaxations for both sensing and non-deterministic
actions, effect-merge relaxations.
z Effect-merge relaxation of a sensing action:
transformation of a sensing action o
s-f
having
two different effect sets, effect
1
(o
s-f
)={f} and
ICAART 2012 - International Conference on Agents and Artificial Intelligence
516

effect
2
(o
s-f
)={¬f}, into the deterministic action
o
s-f-merge
having a single effect set, effect(o
s-f-
merge
)={f, ¬f, ¬unknown_f}.
z Effect-merge relaxation of a non-deterministic
action: transformation of a non-deterministic
action o
nd
having k different effect sets,
effect
i
(o
nd
) i=1, …, k, into the deterministic
action o
nd-merge
having a single effect set,
effect(o
nd-merge
)=
⋃
effect
(o
)
,…,
.
With effect-merge relaxations, every sensing and
non-deterministic action can be transformed into its
corresponding deterministic action. We propose a
new relaxed planning graph built from effect-merge
relaxed actions instead of sensing and non-
deterministic actions.
z Merged Planning Graph (MPG): the merged
planning graph expanded from a belief state b
m
,
during belief space search to solve a contingent
planning problem P
pond
= (b
I
, G, O
d
∪O
nd
∪O
s
),
is built from multiple literal layers and action
layers in the following way:
- The initial literal layer L
0
includes all literals
representing the belief state b
m
.
- The k-th action layer A
k
is built from any
actions o∈ O
d
∪O
nd-merge
∪O
s-merge
whose
every precondition is satisfied with literals
on the k-th literal layer. O
d
denotes the set
of deterministic actions. O
nd-merge
and O
s-
merge
represent the set of effect-merged non-
deterministic actions and the set of effect-
merged sensing actions respectively.
- The (k+1)-th literal layer L
k+1
is built by
adding the delete-relaxed effects of all
actions on the k-th action layer A
k
into the
set of literals on the k-th literal layer L
k
.
- When the literal layer L
k+1
includes all goal
literals in G, or is equal to the literal layer
L
k
, the graph expansion ends. L
k+1
becomes
the last layer of the merged planning graph
for the belief state b
m
.
5 GD HEURISTICS
Computation of our GD(Goal Dependency) heuristic
for a belief state b
m
proceeds parallel to the forward
expansion of a merged planning graph (MPG) from
the belief state b
m
, layer to layer. Whenever the
graph expands a new literal layer L
k
, the set of goal
literals G
k
⊂G put on the layer L
k
is found, and then
the minimal cost to reach G
k
from the belief state b
m
is computed based on the equation (1) and (2).
cost
(
G
)
= cost
(g)
∈
(1)
cost
(
g
)
=min
(
)
+
(
)
g∈effect
(
)
and ∈
}
(2)
In order to estimate the minimal cost to reach the
goal set G
k
, possible positive interactions among
each goals g∈G
k
are analyzed using a data structure
called closeGoals, as illustrated in Figure 5.
Figure 5: An example illustrating the process to compute
GD heuristics.
By summing up the minimal costs to reach the goal
set G
k,
for k=0, ..., n, the GD heuristic for the belief
state b
m
is obtained, as formulated in (3).
h
(
b
)
= cost
(G
)
(3)
Figure 6 and 7 summarize the algorithm for
computing the GD heuristic for a belief state b
m
.
Figure 6: Algorithm for computing GD heuristics.
6 EXPERIMENTS
In order to evaluate the accuracy and computational
efficiency of our GD heuristics based on the merged
planning graphs (MPG), we conducted some
PLANNING GRAPH HEURISTICS FOR SOLVING CONTINGENT PLANNING PROBLEMS
517

Figure 7: Estimate_Cost function.
experiments solving the contingent planning
problems randomly generated from four different
domains. Table 1 shows the reachability cost
estimates of each different heuristic for the same
initial belief state. We notice that the cost estimates
of our GD heuristics are much closer to the actual
minimal costs than those of the max and additive
heuristics, and are not much worse than the overlap
heuristics.
Table 1: Comparison of cost estimates.
Figure 8: Comparison of search space sizes.
Figure 8 compares the search space sizes in terms of
generated states. Our GD heuristics and the overlap
heuristics expanded much smaller search space than
both the max and additive heuristics. This result
implies that our GD and overlap heuristics are much
more informative than the max and additive
heuristics.
Table 2 and 3 compare our GD heuristics with the
overlap heuristics (Hoffmann and Nebel, 2001) in
terms of subgoals generated and actions investigated
during extraction process, respectively. We notice
Table 2: Comparison of generated subgoals.
that the overlap heuristics building a complete
relaxed plan for each belief state consumed much
more computational effort than our GD heuristics.
Table 3: Comparison of investigated actions.
7 CONCLUSIONS
In this paper, we proposed Merged Planning Graphs
(MPGs), and GD heuristics for solving contingent
planning problems. Through experiments in some
problem domains, we showed that GD heuristics are
more informative than the traditional max and
additive heuristics. Moreover, in comparison to the
overlap heuristics, GD heuristics require much less
computational effort for extraction.
ACKNOWLEDGEMENTS
This work was supported by the GRRC program of
Gyeonggi province.
REFERENCES
Bonet, B., Geffner, H., 2001. GPT: A Tool for Planning
with Uncertainty and Partial Information, In IJCAI’01,
International Joint Conference on Artificial
Intelligence. MITPress.
Hoffmann, J., Brafman, R., 2005. Contingent Planning via
Heuristic Forward Search with Implicit Belief States,
In ICAPS’05, International Conference on Automated
Planning and Scheduling. MITPress.
Bryce, D., Kambhampati, S., Smith, D., 2006. Planning
Graph Heuristics for Belief Space Search, Journal of
Artificial Intelligence Research, Vol. 26, pp.35-99.
Bonet, B., Geffner, H., 2005. mGPT: A Probabilistic
Planner Based on Heuristic Search, Journal of
Artificial Intelligence Research, Vol.24, pp.933-944.
ICAART 2012 - International Conference on Agents and Artificial Intelligence
518

Hoffmann, J., Nebel, B., 2001. The FF Planning System:
Fast Plan Generation through Heuristic Search,
Journal of Artificial Intelligence Research, Vol.14,
pp.253-302.
PLANNING GRAPH HEURISTICS FOR SOLVING CONTINGENT PLANNING PROBLEMS
519
