EFFICIENT DESIGN OF BIT-LEVEL ACCELERATOR

ARCHITECTURES FOR THE DEDR-RASF REMOTE SENSING

ALGORITHM USING SUPER-SYSTOLIC ARRAYS

A. Castillo Atoche

, J. Estrada Lopez

, R. Quijano Cetina

and L. Rizo Dominguez

School of Engineering, Autonomous University of Yucatan, Av Industrias No Contaminantes, Merida, Mexico

School of Mathematics, Autonomous University of Yucatan, Av Industrias No Contaminantes, Merida, Mexico

University of Caribe, SM. 78, Mza 1, Lote 1, Cancun, QRoo, Mexico

Keywords: Remote sensing, Parallel computing, Super-systolic arrays, FPGA design.

Abstract: In this paper, we propose bit-level hardware accelerator architectures for real time implementation of large-

scale remote sensing (RS) imaging. The computational complex RS operations of the DEDR-RASF

algorithm are implemented in efficient bit-level high-throughput accelerators units. Super-Systolic Arrays

(SSAs) and High Performance Embedded Computing (HPEC) techniques were used in aggregation with a

HW/SW co-design scheme, achieving the required real-time data processing for newer RS applications. The

bit-level SSA accelerators were implemented in a Virtex 5 XC5VFX130T Field Programable Gate Array

(FPGA) technology. Performance results revels the significant improvement in both area and time metrics

over previous works.

1 INTRODUCTION

Modern adaptive reconstructive signal/image

processing techniques for many current and future

applications of remote sensing in Earth science,

space science, and soon in exploration Science; are

computationally extremely expensive and the

majority of them are not suitable for a real time

implementation with the existing digital signal

processors (DSPs) or personal computers (PCs)

(Henderson and Lewis 1998); (Castillo et al., 2009).

Although computer power has been increased with

the use of Graphic Processor Units (GPUs), the

recent emergence of reconﬁgurable hardware, and in

particular, the commercial availability of Field

Programmable Gate Array (FPGA) chips and

boards, has added a new dimension to the real time

implementation of remote sensing (RS) applications.

Additionally, to address the computational

requirements introduced by many time-critical

applications, several research efforts have been

recently directed towards the incorporation of

parallel computing techniques and the design of

specialized hardware accelerators architectures.

Several strategies have been explored in the

literature to accelerate RS algorithms (Shkyarko

2004a; Valencia and Plaza 2006; Castillo et al.

2009) for high-resolution radar imaging with sensor

arrays and synthetic aperture radar (SAR) systems.

However, there still a challenge to design

specialized hardware accelerators units to perform

real time radar imagery enhancement/reconstruction

tasks.

The focus of this paper is on improving parallel

performance of the fused descriptive experiment

design regularization and robust adaptive space filter

(DEDR-RASF) reconstructive RS algorithm via the

employment of HPEC techniques and the design of

bit-level hardware accelerator architectures pursuing

the real time implementation mode. Sequential

implementations of this algorithm are traditionally

available in radar/SAR simulations scenarios with

model uncertainties previously developed by

(Shkvarko 2004a, 2004b). Such operational

uncertainties are associated with the unknown

statistics of random perturbations of the signals in

the turbulent medium, imperfect array calibration,

finite dimensionality of measurements,

multiplicative signal-dependent speckle noise,

uncontrolled antenna vibrations and random carrier

trajectory deviations in the case of SAR (Wehner

1994); (Henderson and Lewis 1998).

327

Castillo Atoche A., Estrada Lopez J., Quijano Cetina R. and Rizo Dominguez L..

EFFICIENT DESIGN OF BIT-LEVEL ACCELERATOR ARCHITECTURES FOR THE DEDR-RASF REMOTE SENSING ALGORITHM USING

SUPER-SYSTOLIC ARRAYS.

DOI: 10.5220/0003835203270333

In Proceedings of the 2nd International Conference on Pervasive Embedded Computing and Communication Systems (PECCS-2012), pages 327-333

ISBN: 978-989-8565-00-6

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

Our strategy for implementing the bit-level

accelerator architectures in a FPGA platform is

aimed at enhancing the locality through the

utilization of the HPEC techniques to precisely

represent loop programs and to compute complex

sequences of loop transformations (interchange,

fusion, fission, skewing, tiling, etc.) while

preserving the original program semantics and also,

by mapping the transformed algorithmic

representation in super-systolic arrays (SSAs),

which performs the skewer projections in a bit-level

embarrassingly parallel fashion.

2 REMOTE SENSING

BACKGROUND

The general mathematical formalism of the RS

problem and the DEDR-RASF regularization

algorithm is presented in this section. Some crucial

elements that we employ in this paper are similar in

notation and structure to that described in (Shkvarko

2004a, 2004b); (Castillo et al., 2010a), however, this

is necessary for the understanding of the readers.

2.1 Problem Formalism

Let us consider the estimation of the scene pixel-

frame image

via lexicographical reordering

ˆˆ

{}L=Bb

of the spatial spectrum pattern (SSP)

vector estimate

reconstructed from whatever

available measurements of independent realizations

{u(j); j = 1, . . ., J } of the recorded RS data field.

The measurement data wavefield u(y) = s(y) + n(y)

is modelled as a superposition of the echo signals s

and additive noise n that assumed to be available for

observations and recordings within the prescribed

time–space observation domain Y

∋

y, where

(t, )=yp

defines the time–space points in the

observation domain Y = T × P, with T being the

time and P being the sensor position. The

conventional finite-dimensional vector-form

approximation form of the RS data observation

model is given by (Shkvarko 2004a)

u = Se + n (1)

where u, n and e define the vectors composed of the

coefficients of the finite dimensional approximations

of the measurement field u, the observation noise n

and the scene scattered field e, respectively, and S is

the matrix-form approximation of the signal

formation operator (SFO) S specified by the

particular modulation format employed in the RS

system in (Shkvarko 2004a; Castillo et al. 2010a).

The second order statistics b=vect{

ee<>

;

k=1,...,K} of the random scene scattering vector e

has a statistical meaning of the average power

scattering function traditionally referred to as the

spatial spectrum pattern (SSP) of the RS scene

(Wehner 1994). The SSP represents the brightness

reflectivity of the scene image B = L{b}, over the

rectangular scene frame in a conventional pixel

format.

The RS imaging problem is stated as follows: to

find an estimate of the scene pixel-frame image

via lexicographical reordering

= L{

} of the

spatial spectrum pattern (SSP) vector estimate

reconstructed from whatever available

measurements of independent realizations {u

(j)

; j =

1, …, J} of the recorded data vector.

Thus, one can seek to estimate,

, as a discrete-

form representation of the desired SSP, given the

data correlation matrix R

Y pre-estimated

empirically via averaging J ≥ 1 recorded data vector

snapshots {u( j)}( Shkvarko 2004a); and by

determining the solution operator that we also refer

to as the signal formation operator (SFO) F such that

{

}

e diag diag

diag

ˆˆ

{} { }

+++

== =bR FYF FuuF

(2)

where {·}

diag

defines the vector composed of the

principal diagonal of the embraced matrix.

To optimize the search of such SFO F, we

formulate here the following

DEDR strategy

(Shkvarko 2004a)

min{ ( )}→ℜ

(3)

where

{

}

{}

() trace( )( )

trace

ℜ= − −

F FSIAFSI

FR F

(4)

implies the minimization of the weighted sum of the

systematic and fluctuation errors in the desired

estimate

where the selection (adjustment) of the

regularization parameter

α and the weight matrix A

provide the additional experiment design degrees of

freedom incorporating any descriptive properties of

a solution if those are known a priori (Shkvarko

2004a; Castillo et al. 2010a).

2.2 DEDR Regularization Framework

Solving the minimization problem of (3), we obtain

PECCS 2012 - International Conference on Pervasive and Embedded Computing and Communication Systems

328

the desired DEDR-optimized SFO as follows

DEDR

= K

A,α

1−

(5)

where

A,α

111

()

+− −−

SR S A

(6)

defines de so-called reconstruction operator.

Note, that in practical RS scenarios, the additive

observation noise power is adopted for the noise

correlation matrix R

I (Wehner, 1994).

Considering this assumptions, the robust DEDR-

related SFO becomes

DEDR

()N

−− + +

+=Ψ ASKS

(7)

with the discrete-form ambiguity function matrix

operator

=Ψ SS

Furthermore, we can adjust the processing level

degrees of freedom {

,,N

A } which specify a

family of relevant DEDR-related techniques as

follows:

() () ()

diag

() ()

()

()();1,...,.

pp p

bFuuF

Fu Fu

(8)

where



defines the Shur-Hadamar (element by

element) vector-matrix product and

(1) (2) (3)

,,===

MSF RSF RASF

FFFFFF

represents the

conventional matched spatial filtering (MSF), the

robust spatial filtering (RSF) and the robust adaptive

spatial filtering (RASF) methods, respectively. The

derivation of these techniques is next detailed.

2.3 DEDR Reconstructive Techniques

The reconstructed high-resolution DEDR-related

imaging techniques are next described.

MSF. In this method the suppression of noise

dominates over the systematic error in the

optimization problem of (3).

MSF

(1) +

≈FS

(9)

RSF. This method implies preference to any

prior model information (i.e., A = I) and the

systematic and noise error measures is balanced by

adjusting the regularization parameter, e.g.

= , where

b is the prior average gray level

of the image.

RSF

(2) 1

()

−+

=+F Ψ IS

(10)

RASF. In this method, the parameters

and A

are adjusted in an adaptive fashion following the

Bayesian minimum risk strategy (Shkvarko, 2004a);

i.e.,

11 1

ˆˆ

diag ( )

−− −

==AD b

, in which case the SFO

(8) becomes a solution-dependent adaptive operator.

RASF

()N

−− +

+Ψ DS

(11)

Any other feasible adjustments of the DEDR degrees

of freedom provide other possible DEDR-related

SSP reconstruction techniques, that we do not

consider in this paper.

3 EFFICIENT ACCELERATOR

ARCHITECTURES VIA HW/SW

CO-DESGN

In this section, a concise description of efficient

hardware accelerator architectures based on bit-level

super-systolic arrays (SSAs) integrated with the

HW/SW co-design paradigm is presented.

Particularly, we first adapt the DEDR-RASF

algorithm in a co-design scheme applying HPEC

techniques, and then, the selected computationally

complex reconstructive operations are efficiently

implemented in bit-level high-throughput accelerator

architectures. In the design, we propose to use the

FPGA as a high-speed reconfigurable platform.

Following the HW/SW co-design strategy, the

Microblaze embedded processor and the design of

the SSAs as accelerators are employed in the FPGA

platform. These SSAs require high data bandwidth

of data exchange with the embedded processor.

Another challenging task of the co-design is to

manage the large block of data avoiding unnecessary

data transfer from/to the embedded processor

to/from the proposed bit-level HW accelerator.

The main parameters to consider in the

partitioning stage are the task execution speed and

the area required by its HW-level implementation.

Based on those parameter considerations, the

HW/SW co-design is carried out, which consists in

deciding which tasks should be executed in SW and

which one should be implemented by HW. Also, the

fixed-point software stage analysis (i.e., for this

study is employed the selection of 9 bits integer and

23 fractional bits with rounding to nearest format for

all the fixed-point operations) and the C/C++

reference implementation is realized. Remark that

the RS acquired images are stored and loaded from a

compact flash device, and the resulting enhanced

images are also stored to the same memory device.

3.1 HW/SW Co-design Methodology

The first SW co-design stage consist in to analyze

EFFICIENT DESIGN OF BIT-LEVEL ACCELERATOR ARCHITECTURES FOR THE DEDR-RASF REMOTE

SENSING ALGORITHM USING SUPER-SYSTOLIC ARRAYS

329

and implement the DEDR-RASF algorithm. This

reference implementation scheme will be next

compared with the proposed HW/SW co-design

architecture in the FPGA platform.

To implement the fixed-point DEDR-RASF

algorithm (8), we first specify the corresponding

computational procedures in the rectangular scene

frame

(x, y)

∈

R over the azimuth (horizontal

axis,

x) and range direction (vertical axis, y),

respectively. Such multi-stage procedures are

formalized in the following algorithmic scheme as

follows

Algorithm 1: DEDR-RASF algorithm.

Image: (1k×1k)-pixel scene image.

A priori data: N

−

DSS

Result: Reconstructed image

applying DEDR-RASF

technique.

j ← 0

hil

a SAR range frame j<1024 d

Read the SAR range frame u

(

)

Transfer

Hw SSA implementation of

ΨΨ

Transfer

ΨΨ

Compute

RASF

Hw SSA impl. of

()()

=bFu Fu

Transfer

end

The algorithm above shows an outline of the

proposed method. Each computation operation is

preceded by a label indicating where is

computed/implemented the SW/HW operation. The

label

T indicates the transfer to/from the embedded

processor from/to the SSA architecture. The label

represents the operations implemented by the SSAs

and label

S the corresponding operations executed

by the embedded processor.

Additionally, in the partitioning stage, we

address a design implementation that meets all the

specification requirements (functionality, goals and

constraints) looking for the best trade-offs among

the different solutions. From the analysis of the

algorithm 1, we propose to design two SSAs HW

accelerators, i.e., the point spread matrix (PSM)

which implements the computations Ψ

a||Ψr

concurrently over the azimuth and the range

directions and the fixed-point DEDR-RASF

estimator.

Now, we are ready to proceed with the

development of the SSAs using HPEC techniques

for mapping the corresponding RASF algorithm

onto the proposed high-throughput bit-level

accelerators architectures.

3.2 SSA Design

The SSAs is a generalization of the systolic array

(SA). It is a specialized form of an architecture,

where the cells (i.e. processors), compute the data

and store it independently of each other. SSAs

consist of a network of cells (i.e., processing

elements (PE)) in which each cell is conceptualized

as another SA in a bit-level fashion.

Once the partitioning process has been defined

via the HW/SW co-design, a number of different

loop optimization techniques (i.e., loop optimization,

loop unrolling, tiling, loop interchange, etc.) used in

HPEC are implemented in order to exploit the

maximum possible parallelism in the design (see

(Castillo et al. 2010b) for more details).

The first stage of the SSA-based design flow

consists in transforming the nested loop algorithms

of the selected DEDR-RASF operations, in a parallel

algorithmic representation with local and regular

dependencies (Kung 1988; Castillo et al. 2010b).

Next, with the tiling technique, the large-scale index

space is divided into regular tiles (or blocks) of a

real-size RS scene frame, and then traversing the

tiles to cover the whole index space (Kung 1988;

Dutta et al. 2006). Finally, the SA is developed as a

co-processor structure. Kung (1988) proved the

mapping theory to transform from the parallel

algorithm to a fixed-sized SA.

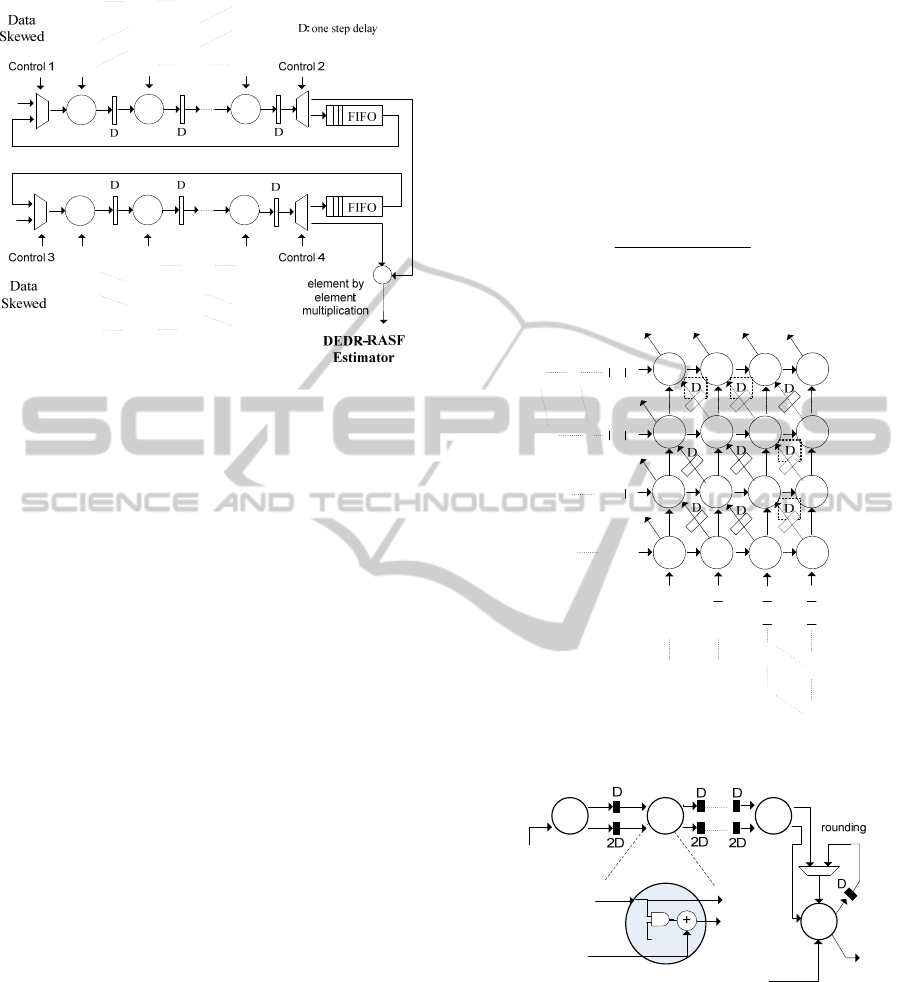
Figure 1 depicts the SA conceptualization of the

fixed-point DEDR-RASF estimator.

From the analysis of Figure 1, one can deduce

the efficient architecture of the reconstructive RS

operations of the DEDR-RASF estimator. The dual-

core SA matrix-vector operations

()()

Fu Fu

(8) are implemented concurrently for each row of

the degraded RS image. Next, both results are

multiplied element by element in a parallel

architecture as also shown in Figure 1. The resulting

SA architecture performs the discrete-form

representation of the desired SSP in a high-

performance structure. Figure 2 shows the SA

architecture of the PSM function.

Having analyzed the PSM architecture of Figure

2, both matrices Ψ

a and Ψr are band-Toeplitz type

matrices (dim{Ψ

a} = Kx × Kx; dim{Ψr} = Ky × Ky)

with the widths of the non-zero strips equal to 2

κa

and 2κr, correspondingly, where due to the PSM

sparseness, 2

κa<< Kx and 2κr<<Ky.

PECCS 2012 - International Conference on Pervasive and Embedded Computing and Communication Systems

330

,1 ,

2,2 1,

2,1 1,2

1,1

mnm

−

−−



1,1

Dual-core SA of F u

()()

=bFu Fu



1, 2

1, m

1,1

1, 2

1,m

1,1

2,1 1,2

2,2 1,

,1 ,

mnm

−−

−



Figure 1: Dual-core SA for the DEDR-RASF estimator.

Once the SAs of the DEDR-RASF algorithm

have been defined, we are ready to conceptualize

and implement the bit-level high-throughput SSAs.

The internal structure of each fixed-sized SA

contains identical linearly-connected PEs. Figure 3

depicts the bit-level SA representation of each PE of

the previously conceptualized PSM and DEDR-

RASF estimator SAs architectures.

The bit-level multiply accumulate (MAC)

structure of each PE is described as follows: the

architecture receives 32-bits operands and generates

64-bits product. Then, the product is truncated to 32-

bits with a fixed-point adopted representation of 9

integers and 24 decimals (i.e., for signed numbers in

two’s complement format) and finally, the result is

rounding for a better performance. The fixed-point

precision guarantees numerical computational errors

less than 10

-5

referring to the MATLAB-based

Fixed-point Toolbox (n.d.) and the Minimum Square

Error (MSE) test.

4 IMPLEMENTATION AND

PERFORMANCE ANALYSIS

4.1 Implementation Results

In the DEDR-RASF algorithmic implementation via

the co-design scheme using SSAs accelerators, we

report the enhancement of the real-world RS images

acquired (Space Imaging n.d.) with different

fractional SAR systems characterized by the PSF of

a Gaussian "bell" shape in both directions of the 2-D

scene (in particular, of 16 pixel width at 0.5 from its

maximum for the 1

k-by-1k BMP pixel-formatted

scene). The images are stored and loaded from a

compact flash device for the image enhancement

process, i.e., particularly for the RSF and RASF

techniques.

In analogy to the image reconstruction, we

employed the quality metric defined as an

improvement in the output signal-to-noise ratio

(IOSNR) (Wehner, 1994):

IOSNR

() 2

()

10log ; 1, 2

()

MSF

−



(12)

Figure 2: SA of the PSM function.

Figure 3: Bit-level SA of the MAC structure.

where

represents the value of the kth element

(pixel) of the original image b,

b represents the

value of the

kth element (pixel) of the degraded

image formed applying the Matched Space Filter

(MSF) technique, and

()

b represents a value of the

kth pixel of the image reconstructed with two

developed methods,

p = 1, 2, where p = 1

1,1

1,2

2,1

2,2

2,3

1,3

3,1

3,2

3,3

1,2

2,1

3,1

1,1

1,2

2,1

1,3

Ψ SS

t-1,p

1,tp

−

t,p

0,1

1,1

,1m

1,1

out

t-1,

t+ ,

,.., ,

m,1 1,1 0,1

aaa

EFFICIENT DESIGN OF BIT-LEVEL ACCELERATOR ARCHITECTURES FOR THE DEDR-RASF REMOTE

SENSING ALGORITHM USING SUPER-SYSTOLIC ARRAYS

331

corresponds to the DEDR-RSF algorithm and p = 2

corresponds to the DEDR-RASF algorithm,

respectively. According to these quality metrics, the

higher are the IOSNR, the better is the improvement

of the image enhancement/reconstructed with the

particular employed algorithms. The initial test

scene is displayed in Figure 4(a). Figure 4(b)

presents the same original image but degraded with

the MSF method. The qualitative HW results for the

RSF and RASF enhancement/reconstruction

procedures are shown in Figures 4(c) and 4(d) with

the corresponding IOSNR quantitative performance

enhancement metrics reported in the figure captions

(in the [dB] scale).

(a) (b)

Figure 4: Results of the HW/SW co-design

implementation for SAR images with 15dB of SNR: (a)

Original test scene; (b) degraded MSF-formed SAR

image; (c) RSF reconstructed image (IOSNR = 7.49 dB);

(d) RASF reconstructed image (IOSNR = 9.14 dB).

4.2 Performance Analysis

In this sub-section, the comparative analysis of the

bit-level specialized HW accelerators using SSAs in

the Xilinx Virtex-5 XC5VFX130T FPGA is next

presented. The achieved architectures are integrated

in the addressed HW/SW co-design approach. The

synthesis metrics related to the implementation of

the SSAs as accelerators are summarized in Table 1.

The parameters of the PSM and DEDR-RASF

estimator modules are specified as follows: data

matrices of size 64×64, data vector of 64×1 and two

Band-Toeplitz PSF matrices of the same 12×12 pixel

size width. Last, it is compared the achieved

processing time of the DEDR-RASF algorithm using

the HW/SW co-design paradigm as reported in

Table 2. In the reported analysis of Table 2, we

consider to use a personal computer (PC) running at

3 GHz with a AMD Athlon (tm) 64 dual-core

processor and 2 GB of RAM memory for the

conventional MATLAB and C++ reference

implementations. In the second case, the same

RSF/RASF algorithms were implemented using the

proposed HW/SW co-design architecture with the

specialized SSAs accelerators in the FPGA platform.

Table 1: Synthesis Metrics: Data matrices of 64×64, data

vector of 64×1 and two band-Toeplitz PSF matrices of

12×12 pixel size width.

SSA

accelerator →

DEDR-RASF

EstimatorModule

PSM

Module

Slices 7757 242

LUTS* 6583 --------

Flip-Flops 5296 480

Frequency

(MHz)

518 576

*LUTs is an acronym to Look Up Tables structures.

Table 2:

Comparative study of time processing.

Method →

Time Processing (Secs)

RSF RASF

Conventional PC-based 13.1 13.4

SSA-based DEDR-RASF

HW/SW co-design

1.10 1.12

The proposed architecture helps to drastically

reduce the overall processing time of the DEDR-

RASF algorithm. In fact, the presented architecture

is efficiently implemented in real time mode in spite

of employing systems based on traditional DSPs or

PC-Clusters platforms (Dawood et al. 2002;

Valencia and Plaza 2006). Particularly, the

implementation of the RASF algorithm using the

proposed architecture takes only 1.12 seconds for

the large-scale RS image reconstruction in contrast

to 13.4 seconds required with the C++

implementation. Thus, the required processing time

of the implementation of the DEDR-RASF

algorithm via the HW/SW co-design using the

specialized accelerators is approximately 12 times

less than the corresponding processing time

achievable with the conventional C++ PC-based

implementation.

5 CONCLUSIONS

The principal result of this study relates to the

conceptualization, design and implementation of

efficient specialized SSAs hardware accelerators.

PECCS 2012 - International Conference on Pervasive and Embedded Computing and Communication Systems

332

The bit-level SSAs are integrated in a HW/SW co-

design scheme for the real-time

enhancement/reconstruction of large-scale remote

sensing (RS) imaging. With the proposed

architecture, the corresponding DEDR-RASF

algorithm was executed in a real time computational

mode (the ‘real-time’ being understood in a context

of conventional RS users). We do believe that

pursuing the aggregation of HPEC and mapping

techniques one could definitely approach the large-

scale real-time image/video processing requirements

while performing the reconstruction of real-world

hyperspectral RS imagery.

ACKNOWLEDGEMENTS

This study was supported by Consejo Nacional de

Ciencia y Tecnología (México) under grant 51234-

CB-2010-01.

REFERENCES

Castillo Atoche, A., Shkvarko, Y. V., Torres, D., Perez, H.

M., 2009, Convex regularization-based

hardware/software co-design for real-time

enhancement of remote sensing imagery, Int. Journal

of Real Time Image Processing, Edit. Springer, vol. 4,

issue 3, pp. 261-272.

Castillo Atoche A., Torres, D., Shkvarko, Y. V., 2010a,

Experiment Design Regularization-Based

Hardware/Software Co-Design for Real-Time

Enhanced Imaging in Uncertain Remote Sensing

Environment’, Eurasip Journal of Advanced Signal

Processing, Edit. Hindawi, Vol. 2010, 21 pages.

Castillo Atoche, A., Torres, D., Shkvarko, Yuriy V.,

2010b, Towards Real Time Implementation of

Reconstructive Signal Processing Algorithms Using

Systolic Arrays Coprocessors, Journal of Systems

Architecture, Edit. Elsevier, vol. 56, issue 8, pp. 327-

339.

Dawood, A. S., Williams, J. A., Visser, S. J., 2002, On-

board Satellite Image Compression Using

Reconfigurable FPGAs, IEEE International

Conference on Field-Programmable Technology, pp.

306-310.

Dutta, H., Hannig, F., Teich, J., 2006, Controller Synthesis

for Mapping Partitioned Programs on Array

Architectures, 19th International Conference on

Architecture of Computing Systems, Germany.

Fixed-Point Toolbox™ User’s Guide, MATLAB:

http://www.mathworks.com.

Henderson, F. M., Lewis, A. V., 1998. Principles and

Applications of Imaging Radar, Wiley, New York, 3

edition.

Kung, S. Y., 1988. VLSI Array Processors, Prentice Hall,

NY.

Shkvarko, Y. V., 2004a. Unifying Regularization and

Bayesian Estimation Methods for Enhanced Imaging

with Remotely Sensed Data. Part I – Theory, IEEE

Transactions on Geoscience and Remote Sensing, vol.

42, issue 5, pp. 923-931.

Shkvarko, Y. V., 2004b. Unifying regularization and

Bayesian estimation methods for enhanced imaging

with remotely sensed data—Part II: Implementation

and performance issues, IEEE Trans. Geoscience and

Remote Sensing, vol. 42, issue 5, pp. 932-940.

Space Imaging, High Resolution Imagery, Earth Imagery

& Geospatial Services. Available online:

http://www.geoeye.com/CorpSite/gallery/default.aspx

?gid=5

Valencia, D. and Plaza, A., 2006, FPGA-based

compression of hyperspectral imagery using spectral

unmixing and the pixel purity index algorithm,

Lecture Notes in Computer Science 3993, pp. 24–31.

Wehner, D. R., 1994, High-Resolution Radar Artech

House, Boston, 2

edition.

EFFICIENT DESIGN OF BIT-LEVEL ACCELERATOR ARCHITECTURES FOR THE DEDR-RASF REMOTE

SENSING ALGORITHM USING SUPER-SYSTOLIC ARRAYS

333