TOWARD SOPHISTICATED AGENT-BASED UNIVERSES

Statements to Introduce some Realistic Features into Classic AI/RL Problems

Filipo Studzinski Perotto

Constructivist Artificial Intelligence Research Group, Toulouse, France

Keywords: Agency theory, Factored Partially Observable Markov Decision Process (FPOMDP), Constructivist learning

mechanisms, Anticipatory learning, Model-based reinforcement learning.

Abstract: In this paper we analyze some common simplifications present in the traditional AI / RL problems. We

argue that only facing particular conditions, often avoided in the classic statements, will allow the

overcoming of the actual limits of the science, and the achievement of new advances in respect to realistic

scenarios. This paper does not propose any paradigmatic revolution, but it presents a compilation of several

different elements proposed more or less separately in recent AI research, unifying them by some theoretical

reflections, experiments and computational solutions. Broadly, we are talking about scenarios where AI

needs to deal with true situatedness agency, providing some kind of anticipatory learning mechanism to the

agent in order to allow it to adapt itself to the environment.

1 INTRODUCTION

Every scientific discipline starts by addressing

specific cases or simplified problems, and by

introducing basic models, necessary to initiate the

process of understanding into a new domain of

knowledge; these basic models eventually evolve to a

more complete theory, and little by little, the research

attains important scientific achievements and applied

solutions. Artificial Intelligence (AI) is a quite recent

discipline, and this fact can be easily noticed by

regarding its history in the course of the years. If in

the 1950s and 1960s AI was the stage for optimistic

discourses about the realization of intelligence in

machine, the 1970s and 1980s reveal an evident

reality: true AI is a feat very hard to accomplish. This

movement led AI to plunge into a more pragmatic and

less dreamy period, when visionary ideas have been

replaced by a (necessary) search for concrete

outcomes. Not by chance, several interesting results

have been achieved in these recent years, and it is

changing the skepticism by a (yet timid) revival of the

general AI field.

If on one hand the AI discourse mood has changed

like a sin wave, on the other hand the academic

practice of AI shows a progressive increment of

complexity with respect to the standard problems.

When the solutions designed to some established

problem become stable, known, and accepted, new

problems and new models are proposed in order to

push forward the frontier of the science, moving AI

from toy problems to more realistic scenarios. Make a

problem more realistic is not just increasing the

number of variables involved (even if limiting the

number of considered characteristics is one of the

most recurrent simplifications). When trying to escape

from AI classic maze problems toward more

sophisticated (and therefore more complex) agent-

based universes, we are led to consider several

complicating conditions, like (a) the situatedness of

the agent, which is immersed into an unknown

universe, interacting with it through limited sensors

and effectors, without any holistic perspective of the

complete environment state, and (b) without any a

priori model of the world dynamics, which forces it to

incrementally discover the effect of its actions on the

system in an on-line experimental way; to make

matters worse, the universe where the agent is

immersed can be populated by different kinds of

objects and entities, including (c) other complex

agents, which can have their own internal models, and

in this case the task of learning a predictive model

becomes considerably harder.

In this paper, we use the Constructivist

Anticipatory Learning Mechanism (CALM), defined

in (Perotto, 2010), to support our assumption. In other

words, we shows that the strategies used by this

method can represent a changing of directions in

433

Studzinski Perotto F..

TOWARD SOPHISTICATED AGENT-BASED UNIVERSES - Statements to Introduce some Realistic Features into Classic AI/RL Problems.

DOI: 10.5220/0003835604330438

In Proceedings of the 4th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2012), pages 433-438

ISBN: 978-989-8425-95-9

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

relation to classic and yet dominant ways. CALM is

able to build a descriptive model of the system where

the agent is immersed, inducting, from the experience,

the structure of a factored and partially observable

Markov decision process (FPOMDP). Some positive

results (Perotto, 2010), (Perotto et al. 2007), (Perotto;

Alvares, 2007), (Perotto, 2011), have been achieved

due to the use of 4 integrated strategies: (a) the

mechanism takes advantage of the situated condition

presented by the agent, constructing a description of

the system regularities relatively to its own point of

view, which allows to set a good behavior policy

without the necessity of “mapping” the entire

environment; (b) the learning process is anchored on

the construction of an anticipatory model of the

world, which could be more efficient and more

powerful than traditional “model free” reinforcement

learning methods, that directly learn a policy; (c) the

mechanism uses some heuristics designed to well

structured universes, where conditional dependencies

between variables exist in a limited scale, and where

most of the phenomena can be described in a

deterministic way, even if the system as a whole is not

(a partially deterministic environment); which seems

to be widely common in real world problems; (d) the

mechanism is prepared to discover the existence of

hidden or non-observable properties of the universe,

which enables it to explain a larger portion of the

observed phenomena. Following the paper, section 2

overviews the MDP framework and the RL tradition,

section 3 describes the CALM learning mechanism,

section 4 shows some experiments and acquired

results, and section 5 concludes the paper.

2 MDP+RL FRAMEWORK

The typical RL problem is inspired on the classic rat

maze experiment; in this behaviorist test, a rat is

placed in a kind of labyrinth, and it needs to find a

piece of cheese (the reward) that is placed somewhere

far from it, sometimes avoiding electric traps along

the way (the punishment). The rat is forced to run the

maze several times, and the experimental results show

that it gradually discovers how to solve it. The

computational version of this experiment corresponds

to an artificial agent placed in a bi-dimensional grid,

moving over it, and eventually receiving positive or

negative reward signals. Exactly as in the rat maze,

the agent must learn to coordinate its actions by trial

and error, in order to avoid the negative and quickly

achieve the positive rewards. This computational

experiment is formally represented by a geographical

MDP, where each position in the grid corresponds to

a state of the process; the process starts in the initial

state, equivalent to the agent start position in the

maze, and it evolves until the agent reaches some

final reward state; then the process is reset, and a new

episode take place; the episodes are repeated, and the

algorithm is expected to learn a policy to maximize

the estimated discounted cumulative reward that will

be received by the agent in subsequent episodes.

These classic RM maze configurations present at

least two positive points, when comparing to realistic

scenarios: the agent needs to learn actively and on-

line, it means, there is no previous separated time to

learn before the time of the life; the agent must

perform and improve its behavior at the same time,

without supervision, by “trial-and-error”. However,

this kind of experiment cannot be taken as a general

scheme for learning: on the one hand, the

simplifications adopted (in order to eliminate some

uncomfortable elements) cannot be ignored when

dealing with more complex or realistic problems; on

the other hand, there are important features lacking on

the classic RL maze, what makes difficult comparing

it to other natural learning situations. Some of these

simplifications and lacks are listed below:

Non-situativity: in the classic RL maze

configuration, the agent is not really situated in the

environment; in fact, the little object moving on the

screen (which is generally called agent) is dissociated

from the “agent as the learner”; the information

available to the algorithm comes from above, from an

external point of view, in which this moving agent

appears as a controllable object of the environment,

among the others. In contrast, realistic scenarios

impose the agent sensory function as an imprecise,

local, and incomplete window of the underlying

situation stated by the real situation.

Geographic Discrete Flat Representation: in

classic mazes, the corresponding MDP is created by

associating each grid cell to a process state; so, the

problem stays confined in the same two dimensions of

the grid space, and the system states represent nothing

more than the agent geographic positions. In contrast,

realistic problems introduce several new and different

dimensions to the problem. The basic MDP model

itself is conceived to represent a system by exhaustive

enumeration of states (a flat representation), and it is

not appropriated to represent multi-dimensional

structured problems; the size of the state space grows

exponentially up with the number of considered

attributes (curse of dimensionality), which makes the

use of this formalism only viable for simple or small

scenarios.

Disembodiment: in the classic configuration, the

agent does not present any internal property, it is like

ICAART 2012 - International Conference on Agents and Artificial Intelligence

434

a loose mind directly living in the environment; in

consequence, it can be only extrinsically motivated,

i.e. the agent acts in order to attain (or to avoid) some

determined positions into the space, given from the

exterior. In natural scenarios, the agent has a “body”

playing the role of an intermediary between mind and

external world; the body also represents an “internal

environment”, and the goals the agent needs to reach

are given from this embodied perspective (in relation

to the dynamics of some internal properties).

Complete Observation: the basic MDP design the

agent as an omniscient entity; the learning algorithm

observes the system in its totality, it knows all the

possible states, and it can precisely perceive in what

state the system is at every moment, it also knows the

effect of its actions on the system, because in general

it is the only source of perturbation in the world

dynamics. These conditions are far from common in

real-world problems.

Episodic Life and Behaviorist Solution: in the

classic enunciation, the system presents initial and

final states, and the agent lives by episodes; when it

reaches a final state, the system restarts. Generally

this is not the case in real-life problems, where agents

live a unique continuous uninterrupted experience.

Also, solving a MDP is often synonymous of finding

an optimal (or near-optimal) policy, and in this way

most of the algorithms proposed in the literature are

model-free. However, in complex environments, the

only way to define a good policy is “understanding”

what is going on, and creating an explicative or

predictive model of the world, which can then be used

to establish the policy.

2.1 The Basic MDP

Markov Decision Process (MDP) and its extensions

constitute a quite popular framework, largely used for

modeling decision-making and planning problems

(Feinberg, Shwartz, 2002). An MDP is typically

represented as a discrete stochastic state machine; at

each time cycle the machine is in some state s; the

agent interacts with the process by choosing some

action a to carry out; then, the machine changes into a

new state s', and gives the agent a corresponding

reward r; a given transition function δ defines the way

the machine changes according to s and a. The flow

of an MDP (the transition between states) depends

only on the system current state and on the action

taken by the agent at the time. After acting, the agent

receives a reward signal, which can be positive or

negative if certain particular transitions occur.

Solving an MDP is finding the optimal (or near-

optimal) policy of actions in order to maximize the

rewards received by the agent over time. When the

MDP parameters are completely known, including the

reward and the transition functions, it can be

mathematically solved by dynamic programming

(DP) methods. When these functions are unknown,

the MDP can be solved by reinforcement learning

(RL) methods, designed to learn a policy of actions

on-line, i.e. at the same time the agent interacts with

the system, by incrementally estimating the utility of

state-actions pairs and then by mapping situations to

actions (Sutton, Barto 1998).

However, for a wide range of complex (including

real world) problems, the complete information about

the exact state of the environment is not available.

This kind of problem is often represented as a

Partially Observable MDP (POMDP) (Kaelbling et

al., 1998). The POMDP provides an elegant

mathematical framework for modeling complex

decision and planning problems in stochastic domains

in which the system states are observable only

indirectly, via a set of imperfect, incomplete or noisy

perceptions. In a POMDP, the set of observations is

different from the set of states, but related to them by

an observation function, i.e. the underlying system

state s cannot be directly perceived by the agent,

which has access only to an observation o. We can

represent a larger set of problems using POMDPs

rather than MDPs, but the methods for solving them

are computationally even more expensive

(Hauskrecht, 2000).

The main bottleneck about the use of MDPs or

POMDPs is that representing complex universes

implies an exponential growing-up on the state space,

and the problem quickly becomes intractable.

Fortunately, most of real-world problems are quite

well-structured; many large MDPs have significant

internal structure, and can be modeled compactly; the

factorization of states is an approach to exploit this

characteristic (Boutilier et al., 2000). In the factored

representation, a state is implicitly described by an

assignment to some set of state variables. Thus, the

complete state space enumeration is avoided, and the

system can be described referring directly to its

properties. The factorization of states enables to

represent the system in a very compact way, even if

the corresponding MDP is exponentially large

(Guestrin et al. 2003). When the structure of the

Factored Markov Decision Process (FMDP) is

completely described, some known algorithms can be

applied to find good policies in a quite efficient way

(Guestrin et al., 2003). However, the research

concerning the discovery of the structure of an

underlying system from incomplete observation is

still incipient (Degris, Sigaud, 2010).

TOWARD SOPHISTICATED AGENT-BASED UNIVERSES - Statements to Introduce some Realistic Features into

Classic AI/RL Problems

435

2.2 FPOMDP

The classic MDP model can be extended to include

both factorization of states and partial observation,

then composing a Factored Partially Observable

Markov Decision Process (FPOMDP). In order to be

factored, the atomic elements of the non-factored

representation will be decomposed and replaced by a

combined set of elements. A FPOMDP (Guestrin et

al., 2001), (Hansen; Feng, 2000), (Poupart;

Boutilier, 2004), (Shani et al., 2005), (Sim et al.,

2008), can be formally defined as a 4-tuple {X, C, R,

T}. The state space is factored and represented by a

finite non-empty set of system properties or

variables X = {X

, X

, ... X

}, which is divided into

two subsets, X = P ∪ H, where the subset P contains

the observable properties (those that can be accessed

through the agent sensory perception), and the

subset H contains the hidden or non-observable

properties; each property X

is associated to a

specified domain, which defines the values the

property can assume; C = {C

, C

, ... C

} represents

the controllable variables, composing the agent

actions; R = {R

, R

, ... R

} is a set of (factored)

reward functions, in the form R

: P

→ IR, and T =

, T

, ... T

} is a set of transformation functions, as

: X × C → X

, defining the system dynamics. Each

transformation function can be represented by a

Dynamic Bayesien Network (DBN), which is an

acyclic, oriented, two-layers graph. The first layer

nodes represent the environment state in time t, and

the second layer nodes represent the next state, in

t+1 (Boutilier et al. 2000). A stationary policy π is a

mapping X → C where π(x) defines the action to be

taken in a given situation. The agent must learn a

policy that optimizes the cumulative rewards

received over a potentially infinite time horizon.

Typically, the solution π* is the policy that

maximizes the expected discounted reward sum.

In this paper, we consider the case where the agent

does not have an a priori model of the universe where

it is situated (i.e. it does not have any idea about the

transformation function), and this condition forces it

to be endowed with some capacity of learning, in

order to be able to adapt itself to the system. Although

it is possible directly learn a policy of actions, in this

work we are interested in model-based methods,

through which the agent must learn a descriptive and

predictive model of the world, and so define a behavior

strategy based on it. Learning a predictive model is

often referred as learning the structure of the problem.

In this way, when the agent is immersed in a

system represented as a FPOMDP, the complete task

for its anticipatory learning mechanism is both to

create a predictive model of the world dynamics (i.e.

inducing the underlying transformation function of

the system), and to define an optimal (or sufficiently

good) policy of actions, in order to establish a

behavioral strategy. Degris and Sigaud (2010) present

a good overview of the use of this representation in

artificial intelligence, referring algorithms designed to

learn and solve FMDPs and FPOMDPs.

3 ANTICIPATORY LEARNING

In the artificial intelligence domain, anticipatory

learning mechanisms refer to methods, algorithms,

processes, machines, or any particular system that

enables an autonomous agent to create an anticipatory

model of the world in which it is situated. An

anticipatory model of the world (also called predictive

environmental model, or forward model) is an

organized set of knowledge allowing inferring the

events that are likely to happen. For cognitive sciences

in general, the term anticipatory learning mechanism

can be applied to humans or animals to describe the

way these natural agents learn to anticipate the

phenomena experienced in the real world, and to adapt

their behavior to it (Perotto, 2012).

When immersed in a complex universe, an agent

(natural or artificial) needs to be able to compose its

actions with the other forces and movements of the

environment. In most cases, the only way to do so is by

understanding what is happening, and thus by

anticipating what will (most likely) happen next. A

predictive model can be very useful as a tool to guide

the behavior; the agent has a perception of the current

state of the world, and it decides what actions to

perform according to the expectations it has about the

way the situation will probably change. The necessity

of being endowed with an anticipatory learning

mechanism is more evident when the agent is fully

situated and completely autonomous; that means, when

the agent is by itself, interacting with an unknown,

dynamic, and complex world, through limited sensors

and effectors, which give it only a local point of view

of the state of the universe and only partial control over

it. Realistic scenarios can only be successfully faced by

an agent capable of discovering the regularities that

govern the universe, understanding the causes and the

consequences of the phenomena, identifying the forces

that influence the observed changes, and mastering the

impact of its own actions over the ongoing events.

3.1 CALM Mechanism

The constructivist anticipatory learning mechanism

ICAART 2012 - International Conference on Agents and Artificial Intelligence

436

(CALM), detailed in (Perotto, 2010), is a mechanism

developed to enable an agent to learn the structure of

an unknown environment where it is situated, trough

observation and experimentation, creating an

anticipatory model of the world. CALM operates the

learning process in an active and incremental way,

and learn the world model as well as the policy at the

same time it actuates. The agent has a single

uninterrupted interactive experience into the system,

over a theoretically infinite time horizon. It needs

performing and learning at the same time.

The environment is only partially observable from

the point of view of the agent. So, to be able to create

a coherent world model, the agent needs, beyond

discover the regularities of the phenomena, also

discover the existence of non-observable variables

that are important to understand the system evolution.

In other words, learning a model of the world is

beyond describing the environment dynamics, i.e. the

rules that can explain and anticipate the observed

transformations, it is also discovering the existence of

hidden properties (once they influence the evolution

of the observable ones), and also find a way to

deduces the dynamics of these hidden properties. In

short, the system as a whole is in fact a FPOMDP,

and CALM is designed to discover the existence of

non-observable properties, integrating them in its

anticipatory model. In this way CALM induces a

structure to represent the dynamics of the system in a

form of a FMDP (because the hidden variables

become known), and there are some algorithms able

to efficiently calculate the optimal (or near-optimal)

policy, when the FMDP is given (Guestrin et al., 2003).

CALM tries to reconstruct, by experience, each

transformation function T

, which will be represented

by an anticipation tree. Each anticipation tree is

composed by pieces of anticipatory knowledge called

schemas, which represent some perceived regularity

occurring in the environment, by associating context

(sensory and abstract), actions and expectations

(anticipations). Some elements in these vectors can

undertake an “undefined value”. For example, an

element linked with a binary sensor must have one of

three values: true, false or undefined (represented,

respectively, by ‘1’, ‘0’ and ‘#’). The learning process

happens through the refinement of the set of schemas.

After each experienced situation, CALM updates a

generalized episodic memory, and then it checks if the

result (context perceived at the instant following the

action) is in conformity to the expectation of the

activated schema. If the anticipation fails, the error

between the result and the expectation serves as

parameter to correct the model. The context and

action vectors are gradually specialized by

differentiation, adding each time a new relevant

feature to identify more precisely the situation class.

The expectation vector can be seen as a label in each

“leaf” schema, and it represents the predicted

anticipation when the schema is activated. Initially all

different expectations are considered as different

classes, and they are gradually generalized and

integrated with others. The agent has two alternatives

when the expectation fails. In a way to make the

knowledge compatible with the experience, the first

alternative is to try to divide the scope of the schema,

creating new schemas, with more specialized

contexts. Sometimes it is not possible and the only

way is to reduce the schema expectation.

CALM creates one anticipation tree for each

property it judges important to predict. Each tree is

supposed to represent the compete dynamics of the

property it represents. From this set of anticipation

trees, CALM can construct a deliberation tree, which

will define the policy of actions. In order to

incrementally construct all these trees, CALM

implements 5 methods: (a) sensory differentiation, to

make the tree grow (by creating new specialized

schemas); (b) adjustment, to abandon the prediction

of non-deterministic events (and reduce the schemas

expectations) (c) integration, to control the tree size,

pruning and joining redundant schemas: (d) abstract

differentiation, to induce the existence of non

observable properties; and (e) abstract anticipation, to

discover and integrate these non-observable properties

in the dynamics of the model.

Sometimes some disequilibrating event can be

explained by considering the existence of some

abstract or hidden property in the environment, which

could be able to differentiate the situation, but which

is not directly perceived by the agent sensors. So,

before adjusting, CALM supposes the existence of a

non-sensory property in the environment, which it

will represent as a abstract element. Abstract elements

suppose the existence of something beyond the

sensory perception, which can be useful to explain

non-equilibrated situations. They have the function of

amplifying the differentiation possibilities.

4 EXPERIMENTS

In (Perotto et al., 2007) the CALM mechanism is used

to solve the flip problem, which creates a scenario

where the discovery of underlying non-observable

states are the key to solve the problem, and CALM is

able to do it by creating a new abstract element to

represent these states. In (Perotto, 2010) and (Perotto;

Álvares, 2007) the CALM mechanism is used to solve

TOWARD SOPHISTICATED AGENT-BASED UNIVERSES - Statements to Introduce some Realistic Features into

Classic AI/RL Problems

437

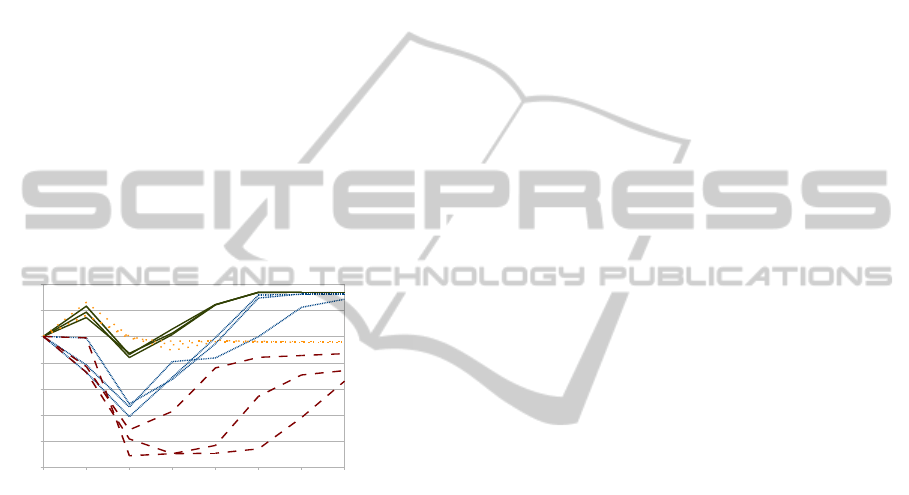
the wepp problem, which is an interesting RL situated

bi-dimensional grid problem, where it should learn

how to behavior considering the interference of

several dimensions of the environment, and of its

body. Initially the agent does not know anything

about the world or about its own sensations, and it

does not know what consequences its actions imply.

Figure 1 shows the evolution of the mean reward

comparing the CALM solution with a classic Q-

Learning implementation (where the agent have the

vision of the entire environment as flat state space),

and with a situated version of the Q-Learning agent.

We see exactly two levels of performance

improvement. First, the non-situated implementation

(Classic Q) takes much more time to start an

incomplete convergence, and it is vulnerable to the

growing of the board. Second, the CALM solution

converges much earlier than Q-Learning, taken in its

situated version, due to the fact that CALM quickly

constructs a model to predict the environment

dynamics, and it is able to define a good policy sooner.

0 10 100 1000 10 mil 100 mil 1 milhão 10 milhões

-1,00

-0,80

-0,60

-0,40

-0,20

0,00

0,20

0,40

wepp

time cycles (logarithmic scale)

mean reward

CALM

Situated Q

Classic Q

Randomic

Figure 1.

5 CONCLUSIONS

Over the last twenty years, several anticipatory

learning mechanisms have been proposed in the

artificial intelligence scientific literature. Even if

some of them are impressive in theoretical terms,

having achieved recognition from the academic

community, for real world problems (like robotics) no

general learning mechanism has prevailed. Until now,

the intelligent artifacts developed in universities and

research laboratories are far less wondrous than those

imagined by science fiction. However, the continuous

progress in the AI field, combined with the progress

of informatics itself, is leading us to a renewed

increase of interest in the search for more general

intelligent mechanism, able to face the challenge of

complex and realistic problems.

A necessary changing of directions in relation to

the traditional ways to state the problems in AI is

needed. The CALM mechanism, presented in

(Perotto, 2010) has been used as an exemple of it,

because it provides autonomous adaptive capability to

an agent, enabling it to incrementally construct

knowledge to represent the regularities observed

during its interaction with the system, even in non-

deterministic and partially observable environments.

REFERENCES

Boutilier, C.; Dearden, R.; Goldszmidt, M. (2000). Stochastic

dynamic programming with factored representations.

Artificial Intelligence, Elsevier, v.121.

Degris, T.; Sigaud, O. (2010). Factored Markov Decision

Processes. In: Buffet, O; Sigaud, O. (eds.). Markov

Decision Processes in Artificial Intelligence.

Vandoeuvre-lès-Nancy: Loria.

Feinberg, E. A.; Shwartz, A. (2002). Handbook of Markov

Decision Processes: methods and applications. Norwell:

Kluwer.

Guestrin, C.; Koller, D.; Parr, R.; Venkataraman, S. (2003).

Efficient Solution Algorithms for Factored MDPs. Journal

of Artificial Intelligence Research. AAAI Press, v.19.

Hauskrecht, M. (2000). Value-function approximations for

partially observable Markov decision processes. Journal

of Artificial Intelligence Research, AAAI Press, v.13.

Hansen, E. A.; Feng, Z. (2000). Dynamic programming for

POMDPs using a factored state representation. In:

Proceedings of 5

AIPS, AAAI Press.

Kaelbling, L. P.; Littman, M. L.; Cassandra, A. R. (1998).

Planning and acting in partially observable stochastic

domains. Artificial Intelligence, Elsevier, v.101.

Perotto, F. S.; Álvares, L. O. (2007). Incremental Inductive

Learning in a Constructivist Agent. In: Proceedings of

SGAI-2006. London: Springer-Verlag.

Perotto, F. S.; Álvares, L. O.; Buisson, J.-C. (2007).

Constructivist Anticipatory Learning Mechanism

(CALM): Dealing with Partially Deterministic and

Partially Observable Environments. In: Proceedings of 7

EPIROB, New Jersey: Lund.

Perotto, F. S. (2010). Un Mécanisme Constructiviste

d'Apprentissage Automatique d'Anticipations pour des

Agents Artificiels Situés. PhD Thesis. Toulouse, France:

INP. (in french)

Perotto, F. S. (2012). Anticipatory Learning Mechanisms. In:

Encyclopedia of the Sciences of Learning, Springer.

Poupart, P.; Boutilier, C. (2004). VDCBPI: an approximate

scalable algorithm for large scale POMDPs. In:

Proceedings of 17th NIPS. Cambridge: MIT Press.

Shani, G.; Brafman, R. I.; Shimony, S. E. (2005). Model-

Based Online Learning of POMDPs. In: Proceedings of

ECML. Berlin: Springer-Verlag. (LNCS 3720).

Sim, H. S.; Kim, K.-E.; Kim, J. H.; Chang, D.-S.; Koo, M.-W.

(2008). Symbolic Heuristic Search Value Iteration for

Factored POMDPs. In: Proc. of 23

AAAI, AAAI Press.

Sutton, R. S.; Barto, A. G. (1998). Reinforcement Learning:

an introduction. MIT Press.

ICAART 2012 - International Conference on Agents and Artificial Intelligence

438