HIGH RESOLUTION SURVEILLANCE VIDEO COMPRESSION

Using JPEG2000 Compression of Random Variables

Octavian Biris and Joseph L. Mundy

Laboratory for Engineering Man-Machine Systems, Brown University, Providence, RI, U.S.A.

Keywords:

JPEG2000, Compression, Background Modeling, Surveillance Video.

Abstract:

This paper proposes a scheme for efﬁcient compression of wide-area aerial video collectors (WAVC) data,

based on background modeling and foreground detection using a Gaussian mixture at each pixel. The method

implements the novel approach of treating the pixel intensities and wavelet coefﬁcients as random variables.

A modiﬁed JPEG 2000 algorithm based on the algebra of random variables is then used to perform the com-

pression on the model. This approach leads to a very compact model which is selectively decompressed only

in foreground regions. The resulting compression ratio is on the order of 16:1 with minimal loss of detail for

moving objects.

1 INTRODUCTION

Recent development of wide-area aerial video col-

lectors (WAVC) that acquire 1.5 Gpixel images at

ten frames per second (Leininger B., 2008) imposes

novel challenges for compression and transmission of

the video data. Acquisition and manipulation of wide

area aerial surveillance video is a challenging task due

to limited on-board storage and bandwidth available

for transferring video to the ground. A collection mis-

sion of two hours produces 350 TeraBytes of data and

a bandwidth of 50 Giga Bytes/sec to record a three-

channel video at 10 frames per second. These high

bandwidth processing and storage requirements war-

rant the need for an efﬁcient compression scheme.

The current approach to managing WAVC data is

to encode the video with JPEG2000 on a frame-by-

frame basis using multiple Analog Devices ADV212

chips, operating on sections of the video frame in par-

allel. However, with lossless compression this ap-

proach results in only a 3:1 compression ratio and

cannot achieve the required frame rate. Applying

higher compression ratios is not feasible since the loss

of ﬁdelity for small moving objects signiﬁcantly re-

duces the performance of automated algorithms, such

as video tracking.

The overall objective of this paper is to describe

an approach to the compression of high resolution

surveillance video using a background model that tol-

erates frequent variations in intensity and also appar-

ent intensity change due to frame mis-registration.

Since total pixel area of moving objects in a scene is

relatively small, an approach based on selectively en-

coding moving objects in each frame and only trans-

mitting a full frame occasionally is likely to produce

a high compression factor. The success of this strat-

egy depends on the ability to accurately detect fore-

ground. It is proposed to use a background model

based on a mixture of Gaussians (GMM), where the

model is compressed using JPEG2000. This approach

leads to an efﬁcient foreground detection algorithm

and a model that is relatively inexpensive to compute

and store.

Alternative strategies such as Motion JPEG and

MPEG-4 Part 10/AVC (also known as H264) video

compression standards are not practical in this appli-

cation. Both methods require the memory storage of

past frames, especially in the case of H-264 which

uses up to 16 bi-predictive frames in motion estima-

tion as well as multiple motion vectors for each block

which point to different reference frames. These ref-

erence frames would have to be stored in high-speed

memory, which is very limited and largely occupied

with the formation of video frames, e.g. Bayer color

restoration.

Several implementations of video compression

based on background-foreground segmentation ex-

ist (Babu and Makur, 2006) (Schwartz et al., 2009)

but none suggest a practical solution for the case of

ultra-high resolution aerial video. Moreover, pixel-

based background models which are less compu-

tationally demanding than block-based models re-

Biris O. and L. Mundy J..

HIGH RESOLUTION SURVEILLANCE VIDEO COMPRESSION - Using JPEG2000 Compression of Random Variables.

DOI: 10.5220/0003840800380045

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 38-45

ISBN: 978-989-8565-03-7

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

quire very large memory. For example, the robust

pixel-based background modeling scheme proposed

by C. Stauffer and W. Grimson (Stauffer and Grim-

son, 1999) uses a mixture of weighted normal distri-

butions at each pixel. Consequently, for a 3-channel

video a model with three mixture components at ev-

ery pixel requires 21 ﬂoating point numbers per pixel,

or a storage of over 130 GBytes per frame.

W.R. Schwartz and H. Pedrini (Schwartz et al.,

2009), extend the motion estimation approach of

Babu on foreground objects by projecting intra-frame

blocks on an eigenspace computed using PCA over a

set of consecutive frames, thus exploiting the spatial

redundancy of adjacent blocks. The cost of estimating

the PCA basis as well as the requirement of observing

foreground-free frames during the estimation process

renders this approach unsuitable.

2 SURVEILLANCE VIDEO

COMPRESSION

In the approach to be described, foreground pixels

are detected using a Gaussian mixture model (GMM),

which provides rapid adaptation to changing imaging

conditions as well as a probabilistic framework. Since

a GMM is stored at each pixel, the storage require-

ment would be prohibitive without some strategy for

model compression. In the following, a technique for

signiﬁcant model data reduction without loss in de-

tection accuracy is described. The description starts

with a review of the GMM background model.

2.1 Background Modeling

The extensive literature on background modeling

methods can be assigned to two major categories.

The ﬁrst one exploits temporal redundancy between

frames by applying a statistical model on each pixel.

Model parameters are estimated either on-line recur-

sively or off-line using maximum likelihood. Al-

though the normal distribution seems sound and in-

expensive at ﬁrst, it cannot cope with wide varia-

tions of intensity values such as reﬂective surfaces,

leaf motion, weather conditions or outdoor illumi-

nation changes. A natural improvement is to use a

mixture of weighted normal distributions(GMMs), a

widely used appearance model for background and

foreground modeling. However, the amount of stor-

age required to maintain a GMM at each pixel is im-

practically large for the WAVC application. In order

for the GMM representation to be effective, the stor-

age requirement must be reduced by at least an order

of magnitude. This paper presents an innovative ap-

proach to the compression of such models in order to

detect moving objects in very large video frames. Be-

fore presenting the new compression method, a sur-

vey of the GMM background modeling approach is

provided as background. Without compression, such

models would require an impractically large amount

of storage.

Friedman and Russell successfully implemented

a GMM background model over a trafﬁc video se-

quence, each parameter being estimated using the

general Expectation-Maximization algorithm (Fried-

man and Russell, 1997). However, the most popu-

lar pixel-based modeling scheme is that implemented

by Stauffer and Grimson (Stauffer and Grimson,

1999), which uses a fast on-line K-means approx-

imation of the mixture parameters. Several varia-

tions of this method were developed improving pa-

rameter convergence rate and overall robustness (Lee,

2005)(Zivkovic, 2004).

The second category of background models ana-

lyzes features from neighboring blocks thus exploit-

ing spatial redundancy within frames. Although

Heikkil

a,and Pietik

ainen (Heikkil

a and Pietik

ainen,

2006) implemented an operator that successfully de-

picts background statistics through a binary pat-

tern, the relatively high computational cost prevent

its use in this application. W.R. Schwartz and H.

Pedrini (Schwartz et al., 2009), propose a method

in which intra-frame blocks are projected on an

eigenspace computed using PCA over a set of consec-

utive frames, thus exploiting the spatial redundancy of

adjacent blocks. The cost of estimating the PCA basis

as well as the requirement of observing foreground-

free frames during the estimation process renders this

approach unsuitable. The same reason makes other

block-based methods that capture histogram,edge, in-

tensity (Jabri et al., 2000)(Javed et al., 2002) and

other feature informations unsuitable for high reso-

lution surveillance video.

In the proposed approach, the background model

is based on a fast-converging extension of the Stauf-

fer and Grimson approximation presented by Dar-

Shyang Lee (Lee, 2005) to model background. The

extension of Lee is explained by starting with a sum-

mary of the basic Stauffer and Grimson algorithm.

The value of each pixel is described by a mixture of

normal distributions. Thus, the probability of observ-

ing a particular color tuple X at time t is given by

Pr(X

) =

K−1

∑

i=0

i,t

· N



,µ

i,t

,Σ

i,t



(1)

K is the number of distributions in the mixture (typi-

cally 3 to 5) and ω

i,t

represents the weight of distribu-

HIGH RESOLUTION SURVEILLANCE VIDEO COMPRESSION - Using JPEG2000 Compression of Random Variables

tion i at time t. Each distribution in the mixture (also

referred to as mixture component) is normal with Pdf :

N (X

,µ,Σ) =

(2π)

|Σ|

exp



−

− µ

)

−1

− µ

)



(2)

The proposed method checks to see if a new incom-

ing pixel color tuple X

t+1

is within a factor f (typ-

ically 2.5) standard deviations from a normal distri-

bution in the mixture. If no match is found the least

weighted component is discarded in favor of a new

one with mean X

t+1

and a high variance. The weights

change according to:

i,t+1

= (1 − α)ω

i,t

+ α · M

i,t

(3)

The value of M

i,t

is 1 for the distribution with the clos-

est match ( if more than one distribution matches, the

one with the highest match ratio (i.e. ω

/|Σ

| ) is cho-

sen and 0 for the rest of the distributions. The learn-

ing rate α represents how fast should the new weight

change when a match is found. Each component i in

the mixture will be updated as follows:

t+1,i

= (1 − ρ

t,i

)µ

t,i

+ ρ

t,i

(4)

t+1

= (1 − ρ

t,i

)Σ

t,i

+ ρ

t,i

− µ

)

− µ

) (5)

Essentially, ρ is the probability of observing the tu-

ple X

given the mixture component i scaled by the

learning rate.

i,t

= αPr(X

|i,θ

i,t

) = αN



,µ

i,t

,Σ

i,t



(6)

The parameter α causes many inaccuracies in various

applications since a small value leads to slow conver-

gence and a large value will make the model sensi-

tive to rapid intensity variations. This problem is ad-

dressed by Lee’s implementation in which each mix-

ture component i has its own adaptive learning rate

which is a function of a global parameter α and a

match count c

i,t

(i.e. the number of times component

i was a match up until the current time t). Let q

i,t

1 if component i is the closest match at time t and 0

otherwise. The weight is updated as follows:

i,t+1

= (1 − α)ω

i,t

+ αq

i,t

(7)

The key difference from the Stauffer and Grimson al-

gorithm is the following update equation,

i,t

= q

i,t



1 − α

i,t

+ α



(8)

Since each component maintains a history of obser-

vations, the convergence rate of the true background

distribution can be achieved much faster while main-

taining robustness in the early stages of learning. The

background model for video frames of dimension

w × h at time t can be regarded as an image of ran-

dom variables

I =

P d f



i j



|i < w , j < h , X

i, j

∼ M (ω

,µ

,Σ

)

(9)

The sample space for each pixel, X

i j

is the set of

all possible color tuples (e.g. all 8-bit RGB value

combinations) and the probability function is the mix-

ture of normal distributions M (ω

,µ

,Σ

). Storing

I losslessly requires a large memory space is not a

practical solution. A highly compressed representa-

tion of I will make implementations tractable but with

the risk of inaccurate classiﬁcation of foreground ob-

jects. As will be seen, JPEG2000 provides an effec-

tive compression scheme, since regions that are de-

tected to contain foreground based on a highly com-

pressed model can be reﬁned locally without decom-

pressing the entire model, and thus obtain the accu-

racy of the original background model.

2.2 The JPEG2000 Standard

JPEG2000 applies a transform (DWT) to the image

and then truncates the bit resolution of the wavelet

coefﬁcients. The coefﬁcients are then encoded using

image neighborhood context analysis followed by

entropy coding. In the case of large single frames,

JPEG2000 has better compression quality, compared

to other coding schemes such as JPEG or H264. The

standard also supports the concept of levels, where

quality can be ﬂexibly balanced with compression

ratio. Additionally the hierarchical nature of the

DWT intrinsically provides an image pyramid, which

is useful for visualizing large images.

A discrete wavelet transform (DWT) decomposes

a signal into low and high frequency coefﬁcients. A

single level of the 2-d transform divides the image

in four high and low frequency subbands along

each direction (e.g. the HL subband emphasizes the

high frequencies in the horizontal direction and low

frequencies in the vertical direction). The subband

that contains low frequencies in both horizontal and

vertical directions (LL) represents a low-pass ﬁltered

and downsampled representation of the original

image. A recursive application of the transform

on the LL band yields a pyramid with multiple

levels of decomposition of the original image. The

subband size in each level is one fourth the size of

corresponding one from the level before.

The effective tiered decomposition of the original

image in JPEG2000 permits its decompression at

various intermediate resolutions before reaching

the original image resolution. Once the wavelet

domain is computed via the lifting scheme with the

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

Daubechies 9/7 or 5/3 wavelet ﬁlters, the coefﬁcients

are quantized and entropy coded. To further achieve

scalability, JPEG2000 introduces the concept of

coding passes when sending wavelet coefﬁcients’ bits

to the entropy encoder. Instead of using a raster-scan

order to code the n

bit of each sample, the coding

passes prioritize the coding of bits that will reduce

distortion the most from the overall image. In the

case of lossy encoding, instead of truncating the

same number of bits for every sample in a region,

JPEG2000 truncates a certain number of coding

passes, effectively performing a ”selective” bit

truncation per sample. Furthermore, JEPG2000 has

a highly hierarchic partitioning policy which permits

random access and decoding of spatial regions in the

codestream.

2.3 Compression of Background Models

Using JPEG 2000

In order to compress the background model, which

is an array of GMM distributions, it is necessary

to derive the associated GMM distribution for the

DWT coefﬁcients at each subband at each level of the

wavelet decomposition. Since the wavelet transform

involves basic arithmetic operations such as addition

and scalar multiplication, the required transform of

the GMM will be evaluated according to the presented

novel technique based on the algebra of random vari-

ables.

2.3.1 Algebra of Random Variables

To obtain the distribution of the sum of two indepen-

dent random variables knowing each of their distribu-

tion, one must convolve one pdf with the other. Math-

ematically,

X+Y

(z) = P

(x) ⊗ P

(y) (10)

The operator ⊗ stands for convolution. Similarly, one

can determine the distribution of an invertible func-

tion g of a random variable as such (Wackerly et al.,

2002):

g(X)

(y) = P

−1

(y)) ·

−1

(y)

(11)

for our purposes let g be a linear function of the form

Y = g(X) = s · X . Thus (11) becomes

Y /s

(12)

Extending these to normally distributed random vari-

ables we have for the sum operator (Weisstein, 2012):

N (X,µ

,Σ

) ⊗ N (Y,µ

,Σ

) = (13)

= N (X +Y,µ

+ µ

,Σ

+ Σ

) (14)

Similarly for scaling:



,µ,Σ



= N



Y,s · µ, s

· Σ



(15)

The order of summation and integration can trans-

posed thus obtaining,

M (θ

) ⊗ M (θ

) =

∑

i=0

(z)

∑

j=0

(x − z)dz

(16)

∑

j=0

∑

i=0

(z)P

(x − z)dz

(17)

∑

j=0

∑

i=0

N (X

,θ

) ⊗ N (X

,θ

)

(18)

Note that the convolution of two mixtures of size m

and n generally yields m · n modes. The scalar multi-

plication of mixtures simply scales each mode thus:

s · M (ω

,µ

,Σ

) = M



,sµ



(19)

2.3.2 The Wavelet Transform of Random

Variables

Based on these operations over random variables, the

distribution for each wavelet coefﬁcient can be ob-

tained. One issue is that convolution of distributions

produces a number of components equal to the prod-

uct of the number of components in each distribu-

tion. It is necessary to prune back the extra compo-

nents. One approach is to delete the lowest weight

components and then re-normalizing the weights of

the remaining components. Alternatively Z. Zhang et

al.(Zhang, 2003) propose an elegant way of merging

modes in a mixture. Essentially, two mixture modes

with weights ω

and ω

will yield a new mode with

weight ω

= ω

+ω

after the merger. The underlying

property of the newly obtained mode is:

Pr(X|k) = ω

Pr(X|i) + ω

Pr(X| j) (20)

Taking the expectation operator on each side will

give out the mean µ

of the new distribution. The

covariance is similarly obtained by solving Σ

E[XX

|k] − µ

Finally we end up with the follow-

ing merger relationships:

= ω

+ ω

(21)



+ µ



= ω



+ µ



+ ω



+ µ



(22)

After each addition operation, the extra modes are

merged until the desired mixture size obtained, e.g.

three or ﬁve components. Using the lifting scheme

HIGH RESOLUTION SURVEILLANCE VIDEO COMPRESSION - Using JPEG2000 Compression of Random Variables

Figure 1: Probability map evaluation using LL5.

the approximate distribution of wavelet coefﬁcients is

obtained. For each frame F in the video, the proba-

bility map P is obtained by evaluating at every pixel

(i, j) Pr(X

i, j

= F

i j

) , i.e. P = Pr(I = F). Threshold-

ing and binarizing P, a mask is obtained to select the

foreground pixels which will be encoded using stan-

dard JPEG2000. According to A. Perera et al.(Perera

et al., 2008) H.264 is reputed to have better perfor-

mance in encoding foreground blocks. However, as

mentioned earlier, its memory costs preclude its ap-

plication in wide area aerial video collection.

It is desirable to work with a JPEG2000 com-

pressed representation of I when obtaining P. A

sound implementation is to store in high speed mem-

ory the lowest resolution LL band (typically LL5 )

and and use its random variables to evaluate the prob-

ability map. Let the lowest LL band in the wavelet

transform decomposition of I be L. Because the size

of L is 2

= 32 times smaller than I, each distribution

in L will be used to measure the probability of the pix-

els in a 32x32 patch in the video frame F. A less accu-

rate probability map will result than the one obtained

using the full model I. However, by taking advantage

of/harnessing the scalability features of JPEG 2000,

the accuracy of this probability map can be increased

according to the method described below. Low prob-

ability pixels are assumed to be due to the result of

actual foreground or possibly due to the inaccuracy

of the distribution in L. Distributions from L are re-

ﬁned by local decompression from the codestream in

order to distinguish true foreground from model in-

accuracy. Pixels that are found to have low probabil-

ity in a frame will have their corresponding distribu-

tion from I determined via local JPEG2000 decom-

pression. The probability for those pixels is then re-

evaluated with the decompressed distributions which

are close to the distributions of the in original model

I, as shown in Figure 1. The model will not be exactly

recovered due to the fact that JPEG2000 irreversible

compression is employed on I.

It is safe to assume that foreground pixels exist

in coherent regions. Therefore it is efﬁcient that a

pixel needing local decompression causes the neigh-

boring distributions to also be decompressed due to

the pyramid structure of the DWT. Thus, the over-

head involved with performing the inverse DWT and

bitplane de-coding is minimized.

3 EXPERIMENTS

In the ﬁrst experiments, data that has been obtained

from a high-deﬁnition video camera is used to eval-

uate the proposed scheme. In a ﬁnal experiment,

the compression performance is evaluated on ARGUS

wide-area aerial video data taken from one of the fo-

cal planes. (Taubman and Marcellin, 2004) As men-

tioned above, if the probability of a certain pixel mea-

sured with L falls below a certain value, the pixel’s

corresponding distribution from the compressed I

is extracted from the codestream. Several experi-

ments have been run with different decision thresh-

olds, namely {0.01 , 0.1 , 0.3 , 0.5 , 0.7 , 0.9 , 0.99}.

Background models were encoded at various bitrates

also starting at 0.05 and ending at 32 bps(bits per

sample ). A 1280 x 720 background model hav-

ing a maximum of three components per mixture and

each component having an independent covariance

matrix takes up 5.5 KB of storage when JPEG2000

compressed at 0.05 bps. A higher rate like 32 bps

will increase the storage cost per frame to 3184 KB.

On the other hand, higher bitrate models require a

smaller number of local decompressions when evalu-

ating foreground probability. It can be noted that even

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

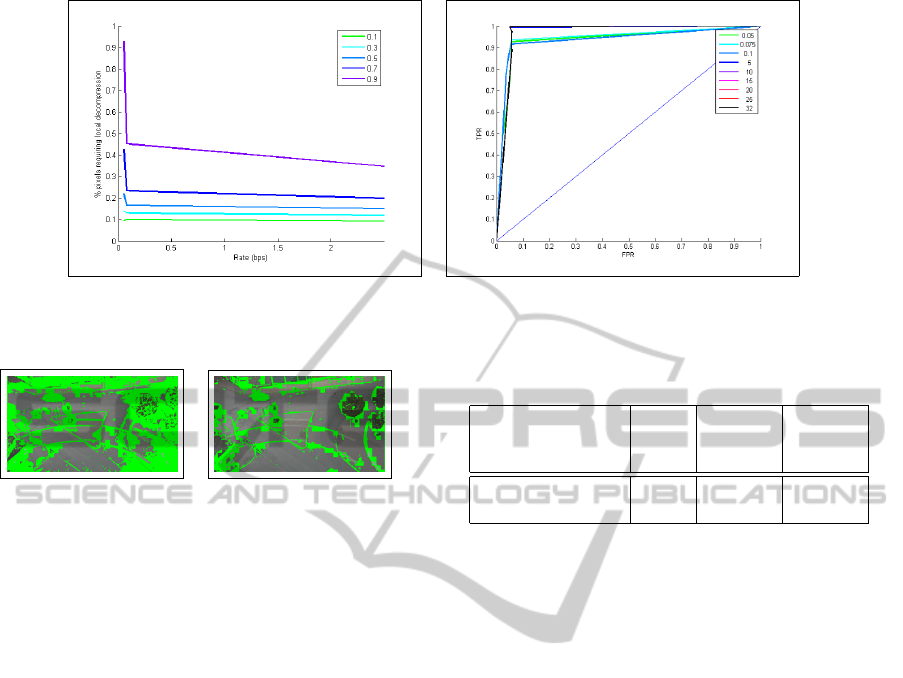
(a) (b)

Figure 2: (a) Percent of pixels requiring local reﬁnement vs. bit rate and (b) ROC characteristic curves for various bitrates.

(a) (b)

Figure 3: Number of local reﬁnements required with a de-

cision threshold of 0.7 and a model compressed at a rate of

(a) 0.05 bps and (b) 32 bps.

the higher rate produces a model that is approximately

100 times smaller than the original GMM and compa-

rable in storage to a single uncompressed color video

frame. The JPEG 2000 library used was D Taubman’s

”Kakadu” 2.2 library (Taubman and Marcellin, 2004)

Figure 3 shows the pixels which require local de-

compression when evaluating the probability map on

one of the frames with two differently encoded back-

ground models. Figure 2 (a) shows that the num-

ber of lookups drops dramatically as bitrate increases

from a fractional value to an integer one. Moreover,

the receiver operator characteristic (ROC) curves in

ﬁgure 2 (b) depict that the True Positive Rate (TPR)

vs. False Positive Rate ( FPR) pairs approach the top

left corner rapidly as a function of the bitrate of the

model used to measure foreground probability. From

both ﬁgures, it is clear that models encoded at bi-

trates ranging from 5bps and above exhibit very simi-

lar characteristics both in the ability to correctly iden-

tify background and the in number of local decom-

pressions required during probability evaluation.

3.1 Results

After each probability map is evaluated with the

method described above, a binary mask is derived

from it via probability thresholding and is applied

on the corresponding frame. The resulting fore-

Table 1: Compression Ratios for two Video Sequences.

Video id Model IVideo

(Lossless )

Video

(lossy @

0.05 bps)

Still 720p Camera 96 4 31

ARGUS City Scene 96 16 87

ground objects are encoded using JPEG2000. Once

every 50 frames the mean image M

t,k

of the highest

weighted component of the background model is en-

coded, where

t,k

= {µ

i j

|i < w , j < h , k = arg max

(ω

i, j

∼ M (ω

,µ

,Σ

)}

Figure 4 shows a video frame and associated proba-

bility map, foreground set and its reconstruction post

compression. A 600 frame 720p video , having each

foreground object losslessly compressed according to

the described method, will reduce its overall storage

reduced by a factor of 4. Each foreground frame

has an average of 0.02 bps. The lossy encoding of

foreground objects is possible, at the expense of re-

construction artifacts. These are due to the fact that

JPEG2000 smooths with each DWT level abrupt tran-

sitions from RGB values at foreground edges to the

0-value background label. This behavior has been re-

ported by Perera et al. (Perera et al., 2008). One solu-

tion is to losslessly encode a binary mask correspond-

ing to the foreground and apply it on the decoded fore-

ground to eliminate the smoothing artifacts. The re-

sults of this masking technique are shown in Figure 5.

A second aerial video sequence,acquired from one of

the ARGUS focal planes, has frame size 2740x2029

and the pixel resolution of moving objects is 25 times

lower than for the stationary camera.

As a consequence, a high compression ratio is

HIGH RESOLUTION SURVEILLANCE VIDEO COMPRESSION - Using JPEG2000 Compression of Random Variables

Figure 4: (a) Mean image M

k,50

. (b) Probability map evaluated with model encoded at 5 bps. (c) Segmented foreground. (d)

Reconstructed frame d = a + c.

(a) (b)

Figure 5: Encoded foreground (a) lossy 0.01 bps (no mask), (b) lossy at 0.01 bps , (c) lossy at 0.05 bps and (d) lossless

achieved since the relative area of moving objects is

much smaller. Scaling the results to the full 1.5 GByte

ARGUS sequence, the encoding of moving objects

requires only 90 MBytes. The results for video and

background model compression are summarized in

Table 1. In each case, moving objects are encoded

with no compression. It should be noted that in the

ARGUS sequence additional bits were spent on en-

coding pixel intensities near discontinuities (edges)

that are labeled as foreground due to frame misalign-

ment.

4 CONCLUSIONS

It has been demonstrated that efﬁcient foreground de-

tection and frame encoding can be achieved by ex-

ploiting the intrinsic mechanisms of the JPEG2000

coding scheme. By encoding the probability distribu-

tions it is possible to reduce the storage cost of GMM

per pixel to the same order as a single video frame.

The resulting accuracy in foreground detection, even

for video that is registered to a single ground plane,

enables a signiﬁcant advance in compression ratio

without sacriﬁcing the quality needed for computer

vision algorithms such as tracking.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

Future work will focus on a GPU implementation

of the proposed algorithm. Pixel-wise and frame-wise

parallelism is inherent will be exploited in the imple-

mentation. Another consideration is to develop algo-

rithms for the lossy encoding of foreground objects

to further improve the compression ratio. As noted

by Perera et al. (Perera et al., 2008), such compres-

sion is not a trivial task since JPEG2000 smooths with

each DWT level abrupt transitions from RGB val-

ues at foreground edges to the 0-value background

label . Moreover, such encoding will inevitably re-

quire closer integration with the computer vision al-

gorithms, such as encoding only the information that

is actually used in tracking.

REFERENCES

Babu, R. V. and Makur, A. (2006). Object-based Surveil-

lance Video Compression using Foreground Motion

Compensation. 2006 9th International Conference on

Control, Automation, Robotics and Vision, pages 1–6.

Friedman, N. and Russell, S. (1997). Image segmentation

in video sequences : A probabilistic approach 1 Intro-

duction. UAI, pages 175–181.

Heikkil

a, M. and Pietik

ainen, M. (2006). A texture-based

method for modeling the background and detecting

moving objects. IEEE transactions on pattern anal-

ysis and machine intelligence, 28(4):657–62.

Jabri, S., Duric, Z., Wechsler, H., and Rosenfeld, A. (2000).

Detection and location of people in video images us-

ing adaptive fusion of color and edge information. In

ICPR’00, pages 4627–4631.

Javed, O., Shaﬁque, K., and Shah, M. (2002). A hierarchi-

cal approach to robust background subtraction using

color and gradient information. In Motion and Video

Computing, 2002. Proceedings. Workshop on, pages

22 – 27.

Lee, D.-S. (2005). Effective gaussian mixture learning for

video background subtraction. IEEE transactions on

pattern analysis and machine intelligence, 27(5):827–

32.

Leininger B., Edwards, J. (2008). Autonomous real-

time ground ubiquitous surveillance-imaging system

(argus-is). In Defense Transformation and Net-

Centric Systems 2008, volume 6981.

Perera, A., Collins, R., and Hoogs, A. (2008). Evaluation of

compression schemes for wide area video. In Applied

Imagery Pattern Recognition Workshop, 2008. AIPR

’08. 37th IEEE, pages 1 –6.

Schwartz, W. R., Pedrini, H., and Davis, L. S. (2009). Video

Compression and Retrieval of Moving Object Loca-

tion Applied to Surveillance. In Proceedings of the 6th

International Conference on Image Analysis (ICIAR),

pages 906–916.

Stauffer, C. and Grimson, W. (1999). Adaptive back-

ground mixture models for real-time tracking. Pro-

ceedings. 1999 IEEE Computer Society Conference

on Computer Vision and Pattern Recognition (Cat. No

PR00149), pages 246–252.

Taubman, D. and Marcellin, M. (2004). JPEG 2000: Im-

age Compression Fundamentals, Standards and Prac-

tice. Kluwer Academic Publishers,Third Printing

2004 ISBN: 9780792375197.

Wackerly, D., Mendenhall, W., and Scheaffer, R.

(2002). Mathematical statistics with applications.

Duxbury -Thomson Learning, ISBN: 0534377416

9780534377410.

Weisstein, E. W. (2012). ”normal sum distribution.

http://mathworld.wolfram.com/NormalSumDistributi

on.html.

Zhang, Z. (2003). EM algorithms for Gaussian mixtures

with split-and-merge operation. Pattern Recognition,

36(9):1973–1983.

Zivkovic, Z. (2004). Improved adaptive Gaussian mixture

model for background subtraction. Proceedings of

the 17th International Conference on Pattern Recog-

nition, 2004. ICPR 2004., pages 28–31 Vol.2.

HIGH RESOLUTION SURVEILLANCE VIDEO COMPRESSION - Using JPEG2000 Compression of Random Variables