MARGINING COMPONENT OF THE STOCK MARKET CRASH

OF OCTOBER 2008

A Lesson of the Struggle with Combinatorial Complexity

Dmytro Matsypura and Vadim G. Timkovsky

The University of Sydney Business School, NSW, Sydney, Australia

Keywords:

Combinatorial, Crash, Margin, Optimization, Market, Mixed, Integer, Program, Risk, Stock, Strategy.

Abstract:

In July 2005 the US stock market started using the risk-based approach to margining customer accounts grad-

ually excluding from margining practice the strategy-based approach, which has been used for more than four

decades. In this paper we argue that this change has a direct link to the stock market crash of October 2008.

We also show that among the main reasons of this change are high strategy-based margin requirements in

comparison with much lower risk-based, the combinatorial complexity of the strategy-based approach, and

the failure of the brokerage industry to adopt the achievements of combinatorial optimization.

1 INTRODUCTION

“We still have a 1930s regulatory system in place.

We’ve got to update our institutions, our regulatory

frameworks, ... the banking system has been ‘dealt

a heavy blow,’ the result of lax regulation, mas-

sive overleverage, huge systematic risks taken by

unregulated institutions, as well as regulated insti-

tutions.” –

Barack Obama

In the margin accounts of investors, margin payments

are based on established minimum margin require-

ments according to the margin rules enforced by the

margin regulations.

Deducting the minimum margin requirement for

an account from its market value we obtain its loan

value, which is the maximum portion of the account’s

market value that the broker can lend. The amount

that is actually lent to a customer by the broker con-

stitute the margin credit. The total margin credit pro-

vided by all brokers in a market constitutes the mar-

ket’s margin debt.

High margin requirements can reduce investors’

activity, lead to underpricing of securities, and cause

economic slowdowns. Low margin requirements, in

turn, lead to overpricing of securities, high levels of

speculation, cash deﬁcits, market crashes, and, again,

economic slowdowns. The challenge for margin reg-

ulators is to ﬁnd a proper approach to margining, a

“golden mean” that keeps the growth of margin debt

within tolerable limits.

Current margining practice uses two approaches,

strategy-based and risk-based.

In comparison with

the strategy-based, the risk-based approach uses sub-

stantially lower margin rates, therefore the ﬁnal ap-

proval of the latter for margining customer accounts

by the SEC

in July 2008, at the time of the global

ﬁnancial crisis, appeared to be one of the most radical

steps in the history of margin regulations.

The goal of this paper is to brieﬂy discuss the dif-

ference between the strategy-based and risk-based ap-

proaches and to illustrate the inﬂuence of risk-based

margin calculations on the stock market crash of Oc-

tober 2008 by considering the margin debt levels in

the period 2005-2008.

2 STRATEGY-BASED APPROACH

The combinatorial essence of the strategy-based ap-

proach arises from the ability to partition a margin ac-

count in different ways in accordance with a large va-

riety of offsets in the margin rule book. The challenge

is to ﬁnd a partition with a minimum total margin of

the offsets and naked positions left uncovered by the

offsets. Each securities market followsits own margin

rule book, for example, NYSE Rule 431 in the U.S. or

Regulation 100 in Canada. The strategy-based offsets

are of ﬁxed size and imitate trading strategies. The ac-

count margin minimization (AMM) problem reduces

to a mixed integer program (MIP) as follows.

484

Matsypura D. and G. Timkovsky V..

MARGINING COMPONENT OF THE STOCK MARKET CRASH OF OCTOBER 2008 - A Lesson of the Struggle with Combinatorial Complexity.

DOI: 10.5220/0003841504840489

In Proceedings of the 1st International Conference on Operations Research and Enterprise Systems (ICORES-2012), pages 484-489

ISBN: 978-989-8425-97-3

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

Let an account have m positions i = 1, 2, . . . , m

in securities with quantities q

and n prime offsets

j = 1, 2, . . . , n. Prime offset j can be represented by

the column vector o

whose ith component o

is the

quantity of the ith component of prime offset j.

Note that o

= 0 if and only if position i is not

involved in prime offset j. We assume that m ≤ n

because we consider that the ﬁrst m prime offsets are

trivial, i.e., they represent positions in security units.

Thus, each of the ﬁrst m column vectors has only one

nonzero element o

j j

= 1.

Let m

be the margin rate for prime offset j. Then

is the margin rate for a security unit in position j

if 1 ≤ j ≤ m. Let x

denote the multiplicity of prime

offset j. If we introduce the vectors

⊤

= ( m

. . . m

)

⊤

= ( q

. . . q

)

⊤

= ( x

. . . x

)

which are the margin, quantity and variable vectors,

respectively, and the offset matrix O = [o

. . . o

]

of size m×n, then the AMM problem can be posed as

ﬁnding an x which solves

min

⊤

x : Ox = q, x ≥ 0

(1)

where 0 is a zero column vector.

Note that O = [I P], where I and P are the iden-

tity matrix, i.e., the matrix of trivial prime offsets, and

the matrix of proper prime offsets, i.e., the matrix of

prime offsets that involve at least two positions, re-

spectively.

In this MIP, components of the variable vector x

from m + 1 to n must be integers because they deﬁne

offset multiplicities, while some of the components

from 1 to m can be real. They are integers if they

are quantities of positions in stocks, options, warrants,

etc., but they can be real if they are, for example, bond

quantities. The quantity vector q is also integer but

the margin vector m is real.

It is important to mention that the components of

the vector m are calculated on the basis of the current

security market prices.

MIP (1) can be viewed as an extension of

the transportation model introduced in (Rudd and

Schroeder, 1982) for the calculation of the minimum

margin by pairing, i.e., in the case where the matrix

of proper prime offsets is a matrix of prime pairs.

Surprisingly, current strategy-based margin cal-

culation practice still uses heuristics designed in the

mid seventies based on brokers’ intuition and taste,

even for margining by pairing. In the general case,

the most advanced heuristics take advantage of the

result from (Rudd and Schroeder, 1982). There ex-

ist, however, examples showing that these heuris-

tics can raise minimum margin requirements to catas-

trophic margin calls. Therefore, margin accounts

maintained by prime brokers up to 2005 with the

use of the strategy-based approach were substantially

over-margined, just because there has been no serious

attempt to ﬁnd efﬁcient optimization algorithms.

Despite the fact that the AMM problem was posed

(originally as a problem of margining accounts with

options only) more than thirty ﬁve years ago, it has

not been well studied and remains one of the most in-

tractable problems in the brokerage industry. Neither

useful theoretical results nor solution techniques with

reasonable computing times are known.

The only exception is the already mentioned pa-

per (Rudd and Schroeder, 1982) devoted to a reduc-

tion of the AMM problem by pairing to the bipartite

minimum-cost network-ﬂow problem and the very re-

cent paper (Matsypura and Timkovsky, 2011) extend-

ing this result to the case with more complex offsets.

An analysis of the literature suggests that the

AMM problem has never been considered in the MIP

form. However, as was shown in (Coffman et al.,

2010b; Coffman et al., 2010a), the MIP for the AMM

problem can be efﬁciently used in practice.

3 RISK-BASED APPROACH

The risk-based approach uses variations of the cur-

rent underlying security prices in an attempt to catch

the worst-case price movements for the entire portfo-

lio. This technique is called portfolio shocking.

According to the portfolio shocking technique, the

margin requirement for each position is the largest

potential loss on this position among the losses cal-

culated for ten valuation points surrounding current

underlying security price. The lowest (highest) valu-

ation points must be

8%(6%), 10%(10%), 15%(15%)

lower (higher) than the current market price for high-

capitalization BBIs

and ETFs

based on it, low-

capitalization BBIs and ETFs based on it, and NBIs

and a margin eligible securities, respectively.

It is important to observe that, in accordance with

this rule, the risk-based margin rate for stocks and

margin eligible equities in customer margin accounts

is only 15%, the lowest margin rate since 1929.

Before the stock market crash of October 1929 it

was 10%. The current strategy-based margin rates

are 50% (initial) and 25% (maintenance).

In our opinion, this signiﬁcant margin reduction

for stock positions and the faulty hedging mechanism

of risk-based offsets for stocks were the main contrib-

utors to the stock market crash of October 2008.

MARGINING COMPONENT OF THE STOCK MARKET CRASH OF OCTOBER 2008 - A Lesson of the Struggle with

Combinatorial Complexity

485

Now let us explain how to calculate the loss on a

position s. Let c

, 1 ≤ v ≤ 11, be one of the eleven

valuation points including the current underlying se-

curity price c. If s is a position in the underlying se-

curity, then the difference o

= c

− c or c− c

shows

the outcome (gain if positive, and loss if negative) as-

sociated with point c

for long or short position s, re-

spectively, for each security unit.

If s is a position in a derivative, then the out-

come o

associated with the valuation point c

should

be calculated in accordance with the mechanism of

the derivative. In most cases, o

is a function of c

, e

(the exercise price of the derivative) and p

(the mar-

ket price of the position s estimated at the valuation

point c

The estimated price p

must be calculated

using a qualiﬁed theoretical pricing model.

Unlike the strategy-based approach, the risk-based

approach uses much looser offsets whose hedging

mechanism is based on the cash settlement only.

A risk-based offset involves all positions with the

same underlying instrument, and the margin require-

ment for this offset is simply the net loss on the in-

volved positions. Thus, for each underlying instru-

ment, a single risk-based offset is the union of all pos-

sible strategy-based offsets.

Without portfolio shocking, the risk-based ap-

proach represents just a relaxed case of the strategy-

based approach with substantially lower rates.

The risk-based approach squeezes the entire rule

book of the strategy-based approach into only one

rule, therefore it allows to substantially simplify cal-

culations of margin requirements for offsets.

With using strategy-based offsets, the risk-based

approach would turn into the extension of the

strategy-based approach adopting the portfolio shock-

ing technique. It would have been natural to use such

an extension in the pilot program for a “cushioned”

transition to the risk-based approach.

4 BRIEF HISTORY PRIOR TO

2005

The strategy-based approach to margining customer

accounts has been used in the brokerage industry for

more than four decades. By the end of the nineties, it

was commonly recognized that this approach yields

excessively high margin requirements. One of the

main reasons for this phenomenon is that the cal-

culation of the minimum regulatory margin by the

strategy-based approach is an intractable combinato-

rial optimization problem that is neither well studied

nor properly understood.

Despite the fact that margin regulations have a

75-year history dating from Regulation T in the Se-

curities Act of 1934, the literature on margin cal-

culations is surprisingly small.

We can point to

only two books (Geelan and Rittereiser, 1998; Curley,

2008) and two papers (Fortune, 2000; Fortune, 2003)

devoted to margining practice, two papers (Moore,

1966; Luckett, 1982) studying the inﬂuence of mar-

gin requirements on investor’s equity ratio, and two

papers (Rudd and Schroeder, 1982; Fiterman and

Timkovsky, 2001) devoted to margining algorithms.

The vast majority of publications on margining prior

to 2005 consisted primarily of regulatory circulares.

Consequently, margin calculation systems, de-

veloped and used in the brokerage industry up to

2005, ignored highly effective and broadly appli-

cable discrete optimization methods. In particular,

the reduction of the AMM problem by pairing to

the minimum-cost network-ﬂow problem (Rudd and

Schroeder, 1982) was seemingly forgotten for more

than 20 years.

As a result, existing margin calculation technol-

ogy, faced with the combinatorial complexity of the

strategy-based approach, failed to take advantage of

efﬁcient combinatorial optimization algorithms. The

vast majority of margin calculation systems used in

the brokerage industry prior to 2005, as our study

shows, used outdated heuristics proposed by brokers

in the mid seventies, cf. (Cox and Rubinsein, 1985;

Geelan and Rittereiser, 1998). But the failure to ﬁnd

an exact solution, as shown in (Coffmanet al., 2010a),

can increase the margin requirement from zero to sev-

eral thousands of dollars.

The risk-based approach was proposed in 1989 by

the OCC

to calculate the net capital requirements

for brokers’ proprietary portfolios of listed options.

It was implemented in 1996 in TIMS

and approved

by the SEC

to be effective as of September 1, 1997.

However, the approach was not used for margining

customer accounts prior to 2005.

Employing lower margin rates and avoiding any

combinatorics in contrast to the strategy-based ap-

proach, the risk-based approach produces substan-

tially lower margin requirements. In the examples

provided by the CBOE, the requirements for naked

options and basic option spreads are at least two or

three times lower.

(72 times lower for a long strad-

dle!) After two NYSE proposals,

the SEC approved

the risk-based approach to margining customer ac-

counts under a temporary pilot program.

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

486

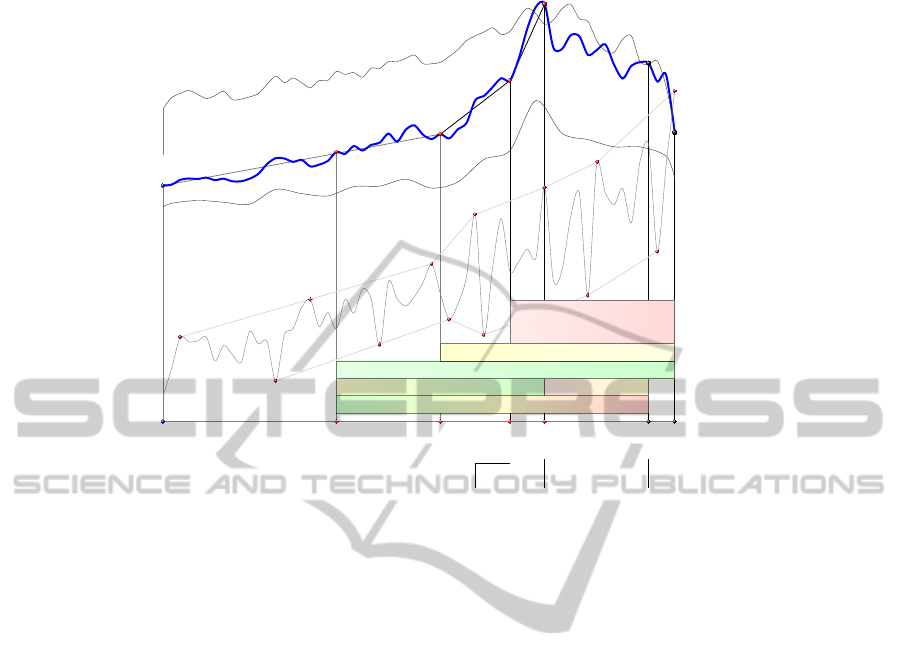
172.14

210.94

231.49

293.16

381.37

314.36

233.35

11-2003 07-2005 07-2006 03-2007

EXCESSIVE

CREDIT

MARKET FALL

07-2007 07-2008 10-2008

risk-based

approach

started

phase II

started

phase III

started

pilot program

extended

risk-based

approach

approved

October stock

market crash

PILOT PROGRAM

ORIGINAL PLAN EXTENSION

I: listed broad based index products, exchange traded funds

II: listed stock options and security futures

III: equities, equity options

unlisted derivatives

narrow based index futures

S&P 500

MARGIN DEBT

MARGIN DEBT / GDP

VOLUME

Figure 1: The margin debt in billions of dollars, the margin debt relative to GDP, and the level and trading volume of the S&P

500 index in the period from November 2003 through October 2008. The curves are scaled to ﬁt on one graph and drawn by

smoothing the end-of-the-month data from http://www.nyse.com/ and http://ﬁnance.yahoo.com/.

5 PILOT PROGRAM OF 2005–2008

The pilot program can be divided into the following

three phases; see Fig. 1:

Phase I started on July 14, 2005 and permitted

the use of the risk-based approach to margin accounts

with only listed BBI and ETF derivatives. Phase II

started on July 11, 2006 and included listed stock op-

tions and securities futures.

Phase III started on

April 2, 2007 and included equities, equity options,

unlisted derivatives and NBI futures.

In contrast with Phases I and II, Phase III was

widely advertised in the media after its approval on

December 12, 2006,

i.e., more than 3 months be-

fore it would become effective. Hence, the substan-

tial decrease of margin requirements for equities, eq-

uity options, all unlisted derivatives and NBI futures

was widely anticipated by numerous investors who

entered the market on April 2, 2007 stimulating de-

mand for stocks and driving the market up.

The pilot program was to expire on July 31, 2007.

However, on July 19, 2007 it was extended for one

more year, and the risk-based approach was ﬁnally

approved to be used permanently on July 30, 2008.

Monthly margin debt reports published by the

NYSE provide clear evidence of the inﬂuence of the

pilot program on the stock market; see Fig. 1. Dur-

ing the initial 20-month period of the pilot program

(July 2005 - April 2007), the margin debt had in-

creased by $82.22 billion compared to the $38.80

billion increase during the previous 20 months. Al-

though the beginning of this period, between the start-

ing points of Phases I and II, looks ordinary, the

ending of this period, between the starting points of

Phases II and III, is remarkable owing to the unusu-

ally high rate of increase in the margin debt and the

trading volume volatility of the S&P 500 index.

During the subsequent four months (April 2007 -

July 2007), the period when equities, equity options,

unlisted derivatives and NBI futures joined the pilot

program, the margin debt increased by another $88.21

billion, i.e., at a rate at least ﬁve times higher. Thus,

since April 2, 2007, the margin debt increased at a

rate of more than $22.05 billion per month.

Historical records show that a fast growth of mar-

gin debt can be a sign of an approaching market crash.

Such was the case in October 1929 and October 1987.

Examining the two most recent examples, consider

the assessments of the market crash of October 2000

in (Geelan and Rittereiser, 1998) (p.87):

“As of February 2000, total margin debt stood at

$265 billion. It had grown 45 percent since the pre-

vious October and had more than tripled since the

end of 1995. Relative to GDP,

margin debt was

MARGINING COMPONENT OF THE STOCK MARKET CRASH OF OCTOBER 2008 - A Lesson of the Struggle with

Combinatorial Complexity

487

the highest it had been since 1929, and over three

times as high as it was in October 1987. It was an

unmistakable sign of rampant speculation.”

Bringing these assertions more up-to-date, we ob-

serve that, as of July 2007, total margin debt stood

at $381 billion. It had grown 30 percent since the pre-

vious March and had almost tripled since the end of

2002. Relative to GDP, margin debt was the highest it

had been since February 2000.

Figure 1 clearly shows that the market credit in the

period from April through July 2007 was excessive in

the extreme: 27% increase in Margin Debt/GDP. Even

though the margin debt reached the level of $381.37

billion by the end of July 2007, the pilot program had,

nevertheless, been extended for an additional year.

In September 2007, it was clear that the growth

in margin debt had lessened because in August 2007

it fell to $331.37 billion as a result, in particular, of

numerous margin calls received by investors and as-

sociated forced sales from their undermargined ac-

counts.

By July 2008, the time of the ﬁnal approval of the

risk-based approach, the margin debt had plunged to

$314.36 billion, signalling an approaching stock mar-

ket downfall. In September 2008 the margin debt had

another plunge from $299.96 to $233.35 billion, and

the stock market downfall was evident as indicated by

the level of S&P 500.

“The task of the Board, as I see it, is to formu-

late regulations with two principal objectives. One

is to permit adequate access to credit facilities for

security markets to perform their basic economic

functions. The other is to prevent the use of stock

market credit from becoming excessive. The latter

helps to minimize the danger of pyramiding credit

in a rising market and also reduces the danger of

forced sales of securities from undermargined ac-

counts in a falling market.” –

W. McC. Martin, Jr.

In July 2007, it was clear that the market credit had

been excessive during the preceding three months: it

had been growing at an unprecedented pace and rel-

ative to GDP had reached its highest level since the

market crash of October 2000. In July 2008, it was

clear that the stock market had been falling for the

previous twelve months. Yet the practice of using the

risk-based approach, which evidently caused exces-

sive market credit, was continuing.

We argue in this paper that the stock market crash

of October 2008 has a direct link to the adoption of

the risk-based approach for margining customer ac-

counts in the US stock market. As shown in our com-

putational experiments with both approaches and ran-

domly generated portfolios (Coffman et al., 2010a),

this approach produces substantially lower margin re-

quirements, especially for investors playing bear.

6 CONCLUDING REMARKS

The results of our research show that the strategy-

based approach is, at this point, the most appropri-

ate one for margining security portfolios in customer

margin accounts because it provides exit strategies.

Over-marginingcan be eliminated by offsetsof higher

sizes and related strategy-based algorithms.

In contrast, the risk-based approach does not pro-

vide exit strategies for security portfolios. In addition,

it can be misleading with respect to the level of risk

exposure of security portfolios.

However, the risk-based approach can work ef-

ﬁciently for margining index portfolios in customer

margin accounts and inventory portfolios of brokers,

because the liquidations of such portfolios do not in-

volve broker-to-broker security movements. It is pos-

sible in the former case because an index itself does

not have trading units. The application of the risk-

based approach to security (including ETFs) portfo-

lios in customer margin accounts is in fact very risky.

We suggest that Phases II and III of the pilot pro-

gram of using the risk-based approach for margining

security portfolios in customer margin accounts were

major contributors to the growth of margin debt in the

period from December 2006 through July 2007 and

the subsequent stock market crash of October 2008.

Margin minimization problems with complex off-

sets can be efﬁciently solved by optimization pack-

ages such as CPLEX. In our opinion, the strategy-

based approach was unjustly discredited by the belief

that the combinatorial problem stemming from the

use of complex offsets could not be efﬁciently solved

with the help of standard optimization packages. Nat-

urally, the development of special optimization algo-

rithms can bring much better results.

The practice of margin calculations has a long his-

tory. However, the science and art of margin calcula-

tions has only just begun to evolve. We hope that this

paper will attract the attention of margin regulators

and academic researchers who are involved in study-

ing efﬁcient exits from the current economic crisis.

REFERENCES

Coffman, Jr., E. G., Matsypura, D., and Timkovsky, V. G.

(2010a). A computational study of margining portfo-

lio of options by two approaches. In Prasad, S. L., Vin,

H. M., Sahni, S., Jaiswal, M. P., and Thipakorn, B.,

editors, Information Systems, Technology and Man-

agement, volume 54 of Communications in Computer

and Information Science, pages 325–332. Springer-

Verlag, Berlin, Heidelberg, 1 edition.

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

488

Coffman, Jr., E. G., Matsypura, D., and Timkovsky, V. G.

(2010b). Strategy vs risk in margining portfolios of

options. 4OR: A Quarterly Journal of Operations Re-

search, 8(4):375–386.

Cox, J. and Rubinsein, M. (1985). Options Markets.

Prentice-Hall.

Curley, M. T. (2008). Margin trading from A to Z. John

Wiley & Sons, New Jersey.

Fiterman, A. E. and Timkovsky, V. G. (2001). Basket

problems in margin calculations: modelling and al-

gorithms. European J. Oper. Res., 129:209–223.

Fortune, P. (2000). Margin requirements, margin loans, and

margin rates: practice and principles. New England

Econ. Rev., pages 19–44.

Fortune, P. (2003). Margin requirements across equity-

related instruments: how level is the playing ﬁeld?

New England Econ. Rev., pages 29–50.

Geelan, J. P. and Rittereiser, R. P. (1998). Margin regula-

tions and practices. NYIF Corporation, Division of

Simon & Schuster, Inc., New York, 4 edition.

Kupiec, P. H. (1998). Margin requirements, volatility and

market integrity: what have we learned since the

crash? J. Financ. Serv. Res., 13(3):231–255.

Luckett, D. G. (1982). On the effectiveness of the federal

reserve’s margin requirements. J. Financ., 37(3):783–

795.

Matsypura, D. and Timkovsky, V. G. (2011). Margining

option portfolios by network ﬂows. Networks. DOI

10.1002/net.

Moore, T. G. (1966). Stock market margin requirements. J.

Polit. Economy, 74(2):158–167.

Rudd, A. and Schroeder, M. (1982). The calculation of min-

imum margin. Manage. Sci., 28(12):1368–1379.

APPENDIX

Notes

1. From “Obama, Brown call for global changes, say ﬁnan-

cial regulations need to be revamped” by Roger Run-

nigen and Robert Hutton, Bloomberg News, p. 4A ·

March 4, 2009 · USA TODAY.

2. The risk-based approach also appears in margin reg-

ulations and business-related literature under the

names “portfolio margining” and “risk-based portfo-

lio margining” approach or methodology. (We omit

the terms “portfolio margining” and “methodology”

for compactness.) The argument standing behind the

term “portfolio” is based on the misrepresentation of

the strategy-based approach as a treatment of a mar-

gin account by considering individual positions only,

while the “portfolio approach” treats a margin account

as a whole. The strategy-based approach also treats a

margin account as a whole; although it does so in a

different way, it is also a portfolio approach. So we

consider the term “risk-based approach” to be most

appropriate. For the same reason, we do not think

that the term “rule-based approach,” frequently used

in the Internet as synonymous with the strategy-based

approach, is suitable because the risk-based approach

is also based on certain rules, such as Rule 15c3-1a or

rules from Regulation T.

3. The U.S. Security and Exchange Commission.

4. Prime offsets have minimum position quantities.

5. Component quantities of prime offsets are integers, un-

like the quantities of convertible securities with non-

integer conversion ratios.

6. The upper index

⊤

denotes the transposition.

7. BBI: Broad Based Index.

8. ETF: Exchange Traded Fund.

9. NBI: Narrow Based Index.

10. These percentages follow Rule 15c3-1a(b)(1)(i)(B).

11. These gains and losses are called “theoretical gains and

losses” in SEC Release 34-53577.

12. For example, if s is a position in a call option, then, after

calculating i

= max{c

− e, 0}, i.e., its in-the-money

amount for valuation point c

, and its estimated market

price p

corresponding to c

, its outcome can be cal-

culated as max{i

, p

} − p, where p is the purchased

price of the call option, multiplied by the option con-

tract size.

13. The model must be approved by the DEA (Designated

Examining Authority). By February 2008, only the

OCC model implemented in STANS was approved,

see Federal Register, Vol 73. No. 29, February 12,

2008.

14. This remark does not refer to the literature devoted to

studying the relationship between margin requirements

and market volatility; see a survey in (Kupiec, 1998).

15. The Options Clearing Corporation.

16. SEC Release 34-27394, October 26, 1989.

17. Theoretical Intermarket Margining System.

18. SEC Releases 34-38248, February 6, 1997.

19. The SEC published the related NYSE proposal for public

comments in SEC Releases 34-46576, October 1, 2002

and 34-50885, December 20, 2004, before approving

the approach in July 2005.

20. www.cboe.com/margin, CBOE Rules 12.4, 9.15(c), 13.5

and 15.8A.

21. SEC Releases 34-46576, October 1, 2002, and 34-50885,

December 20, 2004.

22. SEC Release 34-52031, July 14, 2005.

23. SEC Release 34-54125, July 11, 2006.

24. SEC Release 34-54918.

25. Exchange Act Release No. 58251, July 30, 2008, 73 FR

45506, August 5, 2008.

26. Gross Domestic Product.

27. See, for example, The Wall Street Journal, July-August

2007, for numerous reports on margin calls and asso-

ciated forced sales.

28. From the speech of William McC. Martin, Jr., Chairman

of the Board of Governors of the Federal Reserve Sys-

tem from April 2, 1951, through January 31, 1970, at

the hearing on the study of the stock market before the

U.S. Senate Committee on Banking and Currency on

Monday, March 14, 1955.

MARGINING COMPONENT OF THE STOCK MARKET CRASH OF OCTOBER 2008 - A Lesson of the Struggle with

Combinatorial Complexity

489