RIGID TEMPLATE REGISTRATION IN MET IMAGES USING CUDA

Lennart Svensson, Johan Nysj¨o, Anders Brun, Ingela Nystr¨om and Ida-Maria Sintorn

Centre for Image Analysis, Swedish University of Agricultural Sciences and Uppsala University, Uppsala, Sweden

Keywords:

Three-dimensional Rigid Registration, Normalized Cross Correlation, Molecular Electron Tomography,

CUDA.

Abstract:

Rigid registration is a base tool in many applications, especially in Molecular Electron Tomography (MET),

and also in, e.g., registration of rigid implants in medical images and as initialization for deformable regis-

tration. As MET volumes have a low signal to noise ratio, a complete search of the six-dimensional (6D)

parameter space is often employed. In this paper, we describe how rigid registration with normalized cross-

correlation can be implemented on the GPU using NVIDIA’s parallel computing architecture CUDA. We

compare the performance to the Colores software and two Matlab implementations, one of which is using the

GPU accelerated JACKET library. With well-aligned padding and using CUDA, the performance increases

by an order of a magnitude, making it feasible to work with three-dimensional ﬁtness landscapes, here de-

noted scoring volumes, that are generated on the ﬂy. This will eventually enable the biologists to interactively

1 INTRODUCTION

The imaging modality Molecular Electron Tomogra-

phy (MET) is used for investigating biological struc-

tures, such as proteins or protein complexes, at the

subcellular level. Tomograms are created either from

in vitro buffer solutions of proteins or in situ tissue

samples. For both kinds of volumes, it is difﬁcult to

draw biological conclusions by just visually analysing

the images, as they are rather cluttered, see Figure 1

for an example. Template matching or registration is

often used for searching and identifying objects of in-

terest in the tomograms. The templates can either be

an extracted object from a segmented electron tomog-

raphy volume or be constructed from atomic maps de-

posited in the protein databank (RCSB PDB) (Berman

et al., 2000), which are most often derived from X-ray

crystallography. The atomic data represents the rigid

conformation of the protein as found in a crystal. In

many cases this is close to the natural conformations

molecules appear in, hence rigid template matching

may in many cases be sufﬁcient for the biologists to

understand the volume.

We believe that a semi-automatic or user guided

registration approach is desirable when working with

these volumes, due to the high complexity of both the

tomograms and the investigated biological processes.

The techniques presented in this paper is to be used in

conjunction with earlier presented visualization meth-

Figure 1: Example of an (in situ) MET volume of a desmo-

some holding two skin cells together. The desmosome is a

complex which contains various proteins extending through

the plasma membranes of the neighboring cells it holds to-

gether. In this image the plasma membranes are the two ver-

tical transparent areas, and the complex seen in the centre

of the image contains the extracellular part of the desmo-

some. Antibodies attached to gold particles have been used

to mark the presence of a certain type of protein in the

desmosome. Four gold particles are seen as bright and large

objects in the top middle of the volume.

ods (Svensson et al., 2011), using different projec-

tions of the complete ﬁtness landscape for the 6D pa-

rameter space of 3D rigid registration. These projec-

418

Svensson L., Nysjö J., Brun A., Nyström I. and Sintorn I..

RIGID TEMPLATE REGISTRATION INMET IMAGES USING CUDA.

DOI: 10.5220/0003844804180422

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 418-422

ISBN: 978-989-8565-03-7

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 2: Interactive exploration of an MET volume (left) of the antibody IgG in solution and a score volume showing the

ﬁtness value of the best registration at each position. The user clicks on a point in the right volume and sees the corresponding

registration in the left volume. Iso-surfaces are used to show particular intensity level in both volumes. The middle point in

the right image has the highest intensity. The IgG template is seen in the middle of the MET volume in dark grey.

tions are denoted score volumes. The idea is that the

user will mark a search area in the MET volume and

choose a template where after a complete search will

be performed in this area. The user can then explore

ﬁts by clicking in different score volumes and see the

corresponding registration. This is illustrated in Fig-

ure 2 with a score volume example where each score

represents the best rotational ﬁt of the template at that

position. When the user clicks in the score volume

the template is moved to the corresponding position

and rotated to the best rotation in the search volume.

When a speciﬁc position is selected, a new score vol-

ume for rotational registration can also be calculated

and displayed and help the user see if more than one

rotation of the template are possible (Svensson et al.,

2011). The aim of the interactive approach is to al-

low the user to start analysing the MET volume as

soon as it has been reconstructed, exploring different

templates, placements, and template combinations for

chosen interesting regions. This however creates the

need for close to real-time registration, which has lead

us to investigate GPGPU computation for the task.

CUDA and OpenCL have established themselves

as the two main alternatives for performing general-

purpose on the graphical processing unit (GPGPU)

computations. CUDA is developed by Nvidia for their

graphics cards, and OpenCL is an open standard de-

veloped by an industry consortium. The highest per-

formance is this far reported to have been achieved

using CUDA (Weber et al., 2011). Added the avail-

ability of the FFT library in the CUDA software de-

velopment kit (SDK) has led us to choosing CUDA

for the task.

We compare the speed of our CUDA imple-

mentation with that achieved using standard MAT-

LAB, GPU-accelerated MATLAB using the library

JACKET (JAC, ), as well as with the standard MET

registration software Colores

, (Chac´on and Wrig-

gers, 2002), and (Wriggers, 2010). All are based on

cross-correlation but differ slightly in methodology.

2 TEST DATA

As test data we have created volumes and templates

of sizes corresponding to typical MET experiments.

We have modelled the volumes after the scenario

in (Sandin et al., 2004) where antibodies (IgG) are

searched for in a MET volume image of a solution

containing antibodies. The volumes have a voxel size

of 5.24

A and a resolution of approximately 20A.

Since the computational time for our comparison

of rigid template registration implementations is in-

dependent of image content, we have generated cu-

bic noise images with sizes from 25

to 150

vox-

els. The independence of image content for computa-

tional time holds for the template as well. However,

since one of the comparisons is to the Colores soft-

ware which takes a PDB entry as well as resolution

and voxel size as input, a template created from the

very same PDB entry and with the same parameters

was used in all calculations.

situs.biomachina.org

RIGID TEMPLATE REGISTRATION INMET IMAGES USING CUDA

419

Rotations

Template

Volume

Rotated template

Padded volume Fourier volume

Fourier template Fourier result

Acc. result vol.Norm. vol.

Spatial result

Figure 3: CUDA calculation pipeline. Each box represent one or two buffers in CUDA. Results in boxes with the same color

share memory buffer.

3 CORRELATION METHOD

We have chosen normalized cross-correlation which

is a relatively simple measure that still handles lin-

ear differences between sources well. That is, over-

all differences in intensity mean level and spread be-

tween the template and the search image covered by

the template are compensated for. It is described by

the equation:

s(u) =

∑

(I(x) − I

)(T(x− u) − T)



∑

(I(x) − I

)

∑

(T(x− u) − T)



1/2

(1)

with template T being one rotated instance of the

molecule to register. T is the mean of the template and

is the mean of the region under the template. The

computation of normalized correlation is performed

in the Fourier domain for computational efﬁciency ac-

cording to Lewis (Lewis, 1995).

If the template mean is subtracted from the tem-

plate, then Equation 1 simpliﬁes to

s(u) =

∑

I(x)T(x− u)



∑

(I(x) − I

)

∑

T(x− u)



1/2

. (2)

The numerator corresponds to standard correlation

and is performed for each generated template, i.e.,

each investigated molecule rotation. The denomina-

tor contains the standard deviation for the template

and the volume patch under the template.

4 IMPLEMENTATION

4.1 CUDA

Looking closer at the method, we start with creat-

ing a template using a PDB entry of the speciﬁc

molecule to test. For the tests an IgG antibody tem-

plate was constructed from atom positions in PDB

(entry 1IGT (Harris et al., 1997)) following the proce-

dure by Pittet (Pittet et al., 1999). In brief, the inten-

sity value in each voxel is derived as the sum of con-

tributions from all atoms, each represented by a Gauss

kernel with size corresponding to the atom weight as

well as chosen resolution and voxel size. In this case,

a template of an IgG antibody was constructed in a

cubic image with size 24

voxels.

Figure 3 illustrates how the correlation is imple-

mented using CUDA. The results in boxes with the

same color are using the same memory buffer. All

data is stored in single precision ﬂoating point format.

The mean is ﬁrst subtracted from the template while

in main memory, then both the template and volume is

transferred to GPU memory, with the template being

loaded into a 3D array bound to a texture. In this way,

rotations of the template can be generated using built-

in 3D point lookup with interpolation in textures.

The ﬁrst step on the GPU is calculating the Fourier

transform of the zero-padded search volume using the

CUDA FFT library CUFFT from Nvidia. The base

padding is determined by the size of the template,

with the Fourier volume having size (

volume size

template size

)

. Additional padding is added to

make the Fourier transform fast to compute (well

aligned). The total size of one dimension should be

factorizable into powers of 2 with possible multiplica-

tions of other small prime numbers. The transformed

result is kept during the correlation calculations. The

method then tests one rotation at a time, by rotating

the template and transforming it to the Fourier do-

main. It is multiplied with the transformed search

volume, and the result is transformed back into the

spatial domain. Here, it would be possible to update

the accumulative result in different ways, but for now

we only save the best rotation found at each position.

The normalization is performed on the accumu-

lative result, when all template rotations have been

tested. As Lewis notes (Lewis, 1995), the standard

deviation can be calculated efﬁciently using running

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

420

sums, which can be calculated when rewriting Var(X)

as E[X

] − (E[X])

4.2 Matlab

The implementation we have used is based on an open

source implemention (Eaton, 2011) adapted from the

built-in ’

normxcorr2

’ in Matlab. The algorithm is the

same as for CUDA. Internally Matlab uses the FFTW

library for Fourier transformation. Single precision

ﬂoating point format is used, for fair comparison with

this CUDA implementation. However, the perfor-

mance difference between double and single ﬂoat pro-

cessing on 64-bit processors is quite small today, with

primarily a difference for division operations. Addi-

tionally, we have tested the implementation using the

GPU accelerator Jacket, version 1.8.0

4.3 Colores

Colores is a tool in the program suite Situs for molec-

ular ﬁtting into MET density maps. It uses a slightly

different approach than our Matlab and CUDA imple-

mentations, not aiming at generating score volumes

but a list of candidate positions, which are explored

further using a reﬁnement method. The method still

performs a complete search of the search volume,

so the methods are comparable in terms of perfor-

mance. The reﬁnement step is not included in the

time measurements. We have used Colores in Situs

version 2.6.3. Similarly to Matlab, Colores also uses

the FFTW library for Fourier transformation.

Instead of using the normalized cross-correlation,

Colores applies a Laplace ﬁlter to both volumes as

pre-processing and then performs a standard correla-

tion. This derivative ﬁlter removes low frequencies in

the signal, reducing intensity variation, and increases

the response at edges, which reportedly gives better

results than standard cross-correlation (Chac´on and

Wriggers, 2002) without this additional preprocess-

ing ﬁlter step. However, it can still be sensitive to dif-

ferences in linear scaling of high frequency content.

The padding is set up differently in Colores, yield-

ing a different relation between the size of the in-

put volume and the size of the volume being Fourier

transformed. For smaller input volumes, the Colores

padding is smaller and for larger input volumes, it is

larger. Since the Fourier transformations and the mul-

tiplication in Fourier domain accounts for the major

part of the calculation time, the processing time in

Colores varies accordingly.

www.accelereyes.com/products/jacket

5 COMPARISON

The performance of the different implementations

have been compared on a computer with compara-

ble CPU and GPU in terms of purchase cost. Specif-

ically, the computer had an Intel Xeon E5439 2.66

GHz CPU, 8 GB RAM and an Nvidia Quadro FX

3700 graphics card with 512 MB memory.

All search volumes were constituted of random

values, which is feasible since normalized cross-

correlation is not an adaptive method. As input to

Colores, the volumes have been set to have a voxel

size of 5

nm. The resolution input parameter to Col-

ores was set to 20nm. The Euler angle mode was acti-

vated, with angle distribution according to a spread of

25.8 degrees, giving 994 rotations for each position.

For the CUDA and Matlab versions, 1000 rotations

were used. The CUDA kernels were run using a block

size of 128.

Figure 4: Processing time for different implementations of

rigid registration in relation to size of input volume.

The performance results are shown in Figures 4

and 5, as well as in Table 1. Figure 4 shows a semi

log plot of the processing times for the different im-

plementations for cubic volumes with sizes from 25

to 150

voxels. For the CUDA implementation, we

show the results both for the well-aligned padding

and the base padding. The well-aligned CUDA im-

plementation is the fastest of all compared methods.

The parallel processing in CUDA results in a speed

increase between 6-50 times compared to multi-core

CPU processing in Colores.

The plot in Figure 4 is shown in log scale. There-

fore, the actual times (in seconds) for three volume

sizes, 50

, 100

, and 150

voxels are given in Table 1.

As can be seen in the ﬁgures and the table, the CUDA

implementation using well-aligned padding is faster

than the other methods in the comparison, by around

a factor 10 for larger volumes.

RIGID TEMPLATE REGISTRATION INMET IMAGES USING CUDA

421

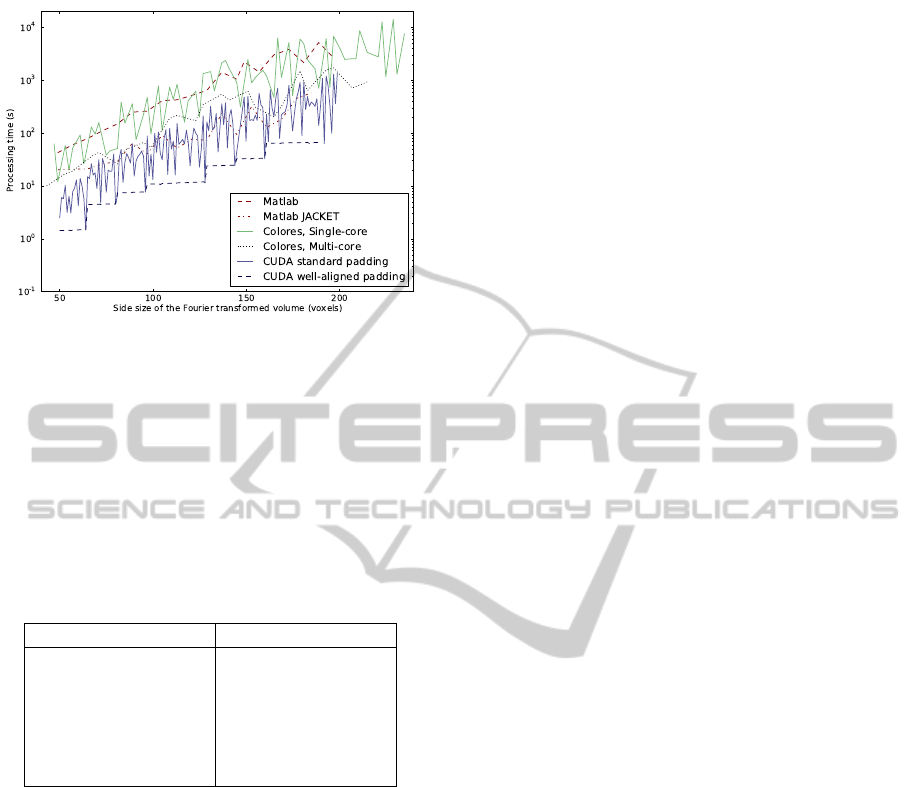
Figure 5: Processing time for different implementations of

rigid registration in relation to size of Fourier transformed

volume.

Additionally, Figure 5 shows the processing time

not for the input size, but for the volume size actually

being Fourier transformed, which differs between the

different methods due to different padding. The well-

aligned CUDA implementation is the fastest in this

comparison as well.

Table 1: Processing time in seconds for different sizes of

the search volume.

Volume size (voxels) 50

100

150

Matlab 273 1354 3577

Matlab JACKET 26 167 513

Colores 1 46 2451 2757

Colores 2 26 623 815

CUDA 1 13 47 156

CUDA 2 4.5 12 65

6 DISCUSSION

We describe an efﬁcient implementation of 3D rigid

template registration based on the normalized cross-

correlation measure using CUDA. This has not, to the

best of our knowledge, been implemented on GPU be-

fore. We compare our implementation with the Col-

ores software and two Matlab implementations, one

of which is using the GPU accelerated JACKET li-

brary. We show the processing times when the same

size of input volume is used as well as when the same

size of the volume actually being Fourier transformed

in the different methods is used. The CUDA im-

plementation with well-aligned padding is the fastest

method in the comparison, with a factor of 10 for

large volumes compared to the Matlab JACKET and

the Colores implementation.

Implementing rigid registration for MET images

on GPU gives a substantial performance increase,

providing a base for advanced interactive image ex-

ploration and analysis of this kind of data in real-time.

The actual registration method requires no input from

the user. In the planned scenarios the user interacts

with the volumes by choosing templates and marks

regions where the registration should be performed.

The rigid search is performed, and within seconds it

will be possible to explore the 3D visualization of the

registration parameter space, the so called score vol-

ume. This is an important step for the interactiveanal-

ysis we have in mind for these volumes. Although the

method and implementation will only be able to han-

dle marked subvolumes due to memory constraints, it

will be possible to subdivide larger volumes and pro-

cess them sequentially, or add another layer of paral-

lelisation using multiple GPU:s.

REFERENCES

Berman, H., Westbrook, J., Feng, Z., Gilliland, G., Bhat, T.,

Weissig, H., Shindyalov, I., and Bournen, P. (2000).

The protein data bank. Nucleic Acids Research,

28:235 – 242.

Chac´on, P. and Wriggers, W. (2002). Multi-resolution

contour-based ﬁtting of macromolecular structures.

Journal of molecular biology, 317(3):375–384.

Eaton, D. (2011). www.cs.ubc.ca/∼deaton/. Accessed on

Oct. 18, 2011.

Harris, L. J., Larson, S. B., Hasel, K. W., and McPherson,

A. (1997). Reﬁned structure of an intact IgG2a mon-

oclonal antibody. Biochemistry, 36(7):1581–1597.

Lewis, J. P. (1995). Fast normalized cross-correlation.

www.scribblethink.org/Work/nvisionInterface/nip.pdf.

Pittet, J.-J., Henn, C., Engel, A., and Heymann, J. B. (1999).

Visualizing 3D data obtained from microscopy on the

internet. Journal of Structural Biology, 125:123–132.

Sandin, S.,

Ofverstedt, L.-G., Wikstr¨om, A.-C., Wrange, O.,

and Skoglund, U. (2004). Structure and ﬂexibility of

individual immunoglobulin G molecules in solution.

Structure, 12:409–415.

Svensson, L., Brun, A., Nystr¨om, I., and Sintorn, I.-M.

(2011). Registration parameter spaces for molecu-

lar electron tomography images. In Image Analysis

and Processing – ICIAP 2011, volume 6978 of LNCS,

pages 403–412.

Weber, R., Gothandaraman, A., Hinde, R., and Peterson, G.

(2011). Comparing hardware accelerators in scientiﬁc

applications: A case study. Parallel and Distributed

Systems, IEEE Transactions on, 22(1):58 –68.

Wriggers, W. (2010). Using situs for the integration

of multi-resolution structures. Biophysical Reviews,

2:21–27.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

422