FUSION OF OPTICAL AND THERMAL IMAGERY AND LIDAR

DATA FOR APPLICATION TO 3-D URBAN ENVIRONMENT

Pattern Recognition Applications in Remotely

Sensed Hyperspectral Image Analysis

Anna Brook

, Marijke Vandewal

, Rudolf Richter

and Eyal Ben-Dor

Royal Military Academy, Department CISS, Brussels, Belgium

German Aerospace Center DLR, Remote Sensing Data Center, Wessling, Germany

Tel-Aviv University, Department of Geography and Human Environment,

Remote Sensing Laboratory, Ramat Aviv, Tel-Aviv, Israel

Keywords: LiDAR, Airborne and ground hyperspectral remote sensing, Airborne and ground thermal remote sensing,

Fuzzy logic, eCognition, Data fusion, 3-D urban environment, 5-D database.

Abstract: Investigation of urban environment includes a wide range of applications that require 3-D information. New

approaches are needed for near-real-time analysis of the urban environment with natural 3-D visualization

of extensive coverage. The remote sensing technology is a promising and powerful tool to assess

quantitative information of urban materials and structures. This technique provides ability for easy, rapid

and accurate in situ assessment of corrosion, deformations and ageing processes in the spatial (2-D) and the

spectral domain within near-real-time and with high temporal resolution. LiDAR technology offers precise

information about the geometrical properties of the surfaces and can reflect the different shapes and

formations in the complex urban environment. Generating a monitoring system that is based on integrative

fusion of hyperspectral, thermal and LiDAR data may enlarge the application envelope of each individual

technology and contribute valuable information on the built urban environment. A fusion process defined by

a data-registration algorithm and including spectral/thermal/spatial and 3-D information has been

developed. The proposed practical 3-D urban environment application may provide urban planners, civil

engineers and decision-makers with tools to consider temporal, quantitative and thermal spectral

information in the 3-D urban space.

1 INTRODUCTION

The most common approach to characterizing urban

environments from remote sensing imagery is land-

use classification. In contrast, mapping the urban

environment in terms of its physical components

preserves the heterogeneity of urban land cover

better than traditional land-use classification

methods (Jensen and Cowen, 1999), characterizes

urban land cover independent of analyst-imposed

definitions and captures more accurately changes

with time.

The spectral (reflective and thermal) properties

of the urban surfaces are known to be rather

complex as they are composed of many materials.

Thematic categories are determined by the principles

of urban mapping, which primarily distinguishes

main types of urban land uses (Roessner et al.,

2001).

The ultimate aim in photogrammetry in

generating an urban landscape model is to show the

objects in an urban area in 3-D (Juan et al., 2007).

As the most permanent features in the urban

environment, an accurate extraction of buildings and

roads is significant for urban planning and

cartographic mapping. Traditionally, the extraction

of buildings relies mainly on manual interpretation,

which remains an expensive and time-consuming

process (Ameri, 2000).

Given the high degree of spatial and spectral

heterogeneity within various artificial and natural

land cover categories, the application of remote

sensing technology to mapping built urban

environments requires specific attention to both 3-D

and spectral domains (Segl et al., 2003). Segl

confirms that profiling hyperspectral TIR can

394

Brook A., Vandewal M., Richter R. and Ben-Dor E..

FUSION OF OPTICAL AND THERMAL IMAGERY AND LIDAR DATA FOR APPLICATION TO 3-D URBAN ENVIRONMENT - Pattern Recognition

Applications in Remotely Sensed Hyperspectral Image Analysis.

DOI: 10.5220/0003845003940405

In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods (PRARSHIA-2012), pages 394-405

ISBN: 978-989-8425-98-0

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

successfully identify and discriminate a variety of

silicates and carbonates, as well as variations in the

chemistry of some silicates. The integration of

VNIR-SWIR and TIR results can provide useful

information to remove possible ambiguous

interpretations in unmixed sub-pixel surfaces and

materials.

Hyperspectral thermal infrared (TIR) remote

sensing has rapidly advanced with the development

of airborne systems and follows years of laboratory

studies (Hunt and Vincent, 1968; Conel, 1969,

Salisbury et al., 1987). The radiance emitted from a

surface in thermal infrared (4-13μm) is a function of

its temperature and emissivity. Emittance and

reflectance are complex processes that depend not

only on the absorption coefficient of materials but

also on their reflective index, physical state and

temperature. Most urban built environment studies

are taking into account both temperature and

emissivity variations, since these relate to the targets

identification, mapping and monitoring and provide

a mean for practical applications.

The hyperspectral thermal imagery provides the

ability for mapping and monitoring temperatures

related to the man-made materials. The urban heat

island (UHI) has been one of the most studied and

best-known phenomena of urban climate

investigated by thermal imagery (Carlson et al.,

1981; Vukovich, 1983; Kidder and Wu, 1987; Roth

et al., 1989; Nichol, 1996). The preliminary studies

have reported similarities between spatial patterns of

air temperature and remotely sensed surface

temperature (Nichol, 1994), whereas progress

studies suggest significant differences, including the

time of day and season of maximum UHI

development and the relationship between land use

and UHI intensity (Roth et al., 1989). The recent

high-resolution airborne systems determine the

thermal performance of the building that can be used

to identify heating and cooling loss due to poor

construction, missing or inadequate insulation and

moisture intrusion.

Over the last few years, LiDAR (LIght Detection

And Ranging) has been widely applied in the field of

photogrammetry and urban 3-D analysis (Tao, 2001,

Zhou, 2004). Airborne LiDAR techniques provide

geo-referenced 3-D dense points (“cloud”) measured

roughly perpendicular to the direction of flight over

a reflective surface on the ground. This system

integrates three basic data-collection tools: a laser

scanner, a global positioning system (GPS) and an

inertial measuring unit (IMU). The position and

altitude of the system being determined by

GPS/INS, the raw data are collected in the GPS

reference system WGS 84.

The main objectives of many studies are linked

to, and rely on a historical set of remotely sensed

imagery for quantitative assessment and spatial

evolution of an urban environment (Jensen and

Cowen, 1999, Donnay et al., 2001, Herold et al.,

2003, 2005).

This paper presents a 3-D urban environment

application. The ability to include an accurate and

realistic 3-D position, quantitative spectral

information, thermal properties and temporal

changes is provided by a near-real-time monitoring

system for photogrammetric and urban planning

purposes. The task for a fully controlled and realistic

monitoring system led us first to combine the image-

processing and map-matching procedures, and then

to incorporate remote sensing and GIS tools into an

integrative method for data fusion.

2 MATERIALS AND METHODS

2.1 Study Area

Two separate datasets were utilized in this study.

The first dataset was acquired over the suburban

area of Ma'alot Tarshiha (33°00'52''N/35°17'E), an

urban settlement in the north of Israel, on 10 Oct

2006 at 03h37 UTC and at 11h20 UTC. This area

combines natural and engineered terrains (average

elevation of 560m above sea level), a hill in the

north of the studied polygon area and a valley in the

center. The entire scene consists of rows of terraced

houses located at the center of the image. The

neighborhood consists of cottage houses (two and

three floors) with tile roofs, flat white-colored

concrete roofs and balconies, asphalt roads and

parking lots, planted and natural vegetation, gravel

paths and bare brown forest soil. The height of large

buildings ranges from 8 to 16 m. A group of tall pine

trees with various heights and shapes are located on

the streets and the Mediterranean forest can be found

in the corner of the scene.

The second dataset was acquired over the area of

Qalansawe (32°01'40''N/35°30'E), an urban

settlement in the center of Israel, on 15 Aug 2007 at

02h54 UTC and at 12h30 UTC. This area combines

natural, agriculture and engineered terrains (average

elevation of 30m above sea level). The urban

settlement consists of houses (two and three floors)

and public buildings (schools and municipalities

buildings) with flat concrete, asphalt or whitewash

roofing, asphalt roads and parking lots, planted and

natural vegetation, gravel paths, bare brown reddish

FUSION OF OPTICAL AND THERMAL IMAGERY AND LIDAR DATA FOR APPLICATION TO 3-D URBAN

ENVIRONMENT - Pattern Recognition Applications in Remotely Sensed Hyperspectral Image Analysis

395

Mediterranean and agriculture soils, greenhouses

and whitewash henhouse roofing. The height of

large buildings ranges from 3 to 21 m.

2.2 Data-acquisition Systems

The research combines airborne and ground data

collected from different platforms and different

operated systems. The collected imagery data were

validated and compared to the ground truth in situ

measurements collected during the campaigns.

The first airborne platform combines two

hyperspectral systems: AISA-Dual and TIR system.

The airborne imaging spectrometer AISA-Dual

(Specim Ltd.) is a dual hyperspectral pushbroom

system, which combines the Aisa EAGLE (VNIR -

Visible and Near Infrared region) and Aisa HAWK

(SWIR - Short Wave Infrared region) sensors. For

the selected campaigns, the sensor simultaneously

acquired images in 198 contiguous spectral bands,

covering the 0.4 to 2.5 µm spectral region with

bandwidths of ~10 nm for Aisa EAGLE and ~5 nm

for Aisa HAWK. The sensor altitude was 10,000 ft,

providing a 1.6 m spatial resolution for 286 pixels in

the cross-track direction. A standard AISA-Dual

dataset is a 3-D data cube in a non-earth coordinate

system (raw matrix geometry).

The airborne hyperspectral TIR system, installed

next to the AISA-Dual sensor on the same platform,

is a line-scanner with 28 spectral bands in the

thermal ranges 3-5 μm and 8-13 μm. It has 328

pixels in the cross-track direction and hundreds of

pixels in the along-track direction with a spatial

resolution of 1.4m.

The second airborne platform carries the LiDAR

system. This system operates at 1500 nm

wavelength with a 165 kHz laser repetition rate and

100 Hz scanning rate and provides a spatial/footprint

resolution of 0.5 m and an accuracy of 0.1 m. The

scanner has a multi-pulse system that could record

up to five different returns, but in this study, only the

first return was recorded and analyzed.

The ground spectral camera HS (Specim Ltd.) is

a pushbroom scan camera that integrates ImSpector

imaging spectrograph and an area monochrome

camera. The camera's sensitive high speed interlaced

CCD (Charge-Coupled Device) detector

simultaneously acquires images in 850 contiguous

spectral bands and covers the 0.4 to 1 µm spectral

region with bandwidths of 2.8 nm. The spatial

resolution is 1600 pixels in the cross-track direction,

and the frame rate is 33 fps with adjustable spectral

sampling.

The ground truth reflectance data were measured

for the calibration/validation targets by the ASD

"FieldSpec Pro" (ASD.Inc, Boulder, CO) VNIR-

SWIR spectrometer. Internally averaged scans were

100 ms each. The wavelength-dependent signal-to-

noise ratio (S/N) is estimated by taking repeat

measurements of a Spectralon white-reference panel

over a 10-min interval and analyzing the spectral

variation across this period. For each sample, three

spectral replicates were acquired and the average

was used as the representative spectrum. The ground

truth thermal data were collected by a thermometer

and thermocouples installed within

calibration/validation targets (water bodies) and a

FLIR thermal infrared camera (FLIR Systems, Inc.).

2.3 Data Processing

This research integrates multi-sensor (airborne

sensor, ground camera and field devices) and multi-

temporal information into a fully operational

monitoring application. The aim of this sub-

paragraph is to present several techniques for

imagery and LiDAR data processing.

2.3.1 Hyperspectral Imagery

Accurate spectral reflectance information is a key

factor in retrieving correct thematic results. The

AISA-Dual images were subjected to the full-chain

SVC (Supervised Vicarious Calibration) calibration

method (Brook and Ben-Dor, 2011a) via

deshadowing algorithm using the shadow map

provided by the boresight ratio band (Brook and

Ben-Dor, 2011b). Operation of the full procedural

sequence extracts recalibration factors from the

master SVC site image and then later applied to the

study areas (imagery acquired during the same

airborne campaign). As for the HS ground camera

the nets were stretched on transportable

Figure 1: Flow chart scheme of the classification approach

for the hyperspectral airborne and ground data.

AISA-Dual Images

Initial Classification

Pure Pixels Map

Unclassified Pixels Map

Sequential Forward Selection

Spectral Unmixing

SVM Probabilistic Map

Spectral Reduction

HS ImagesInput:

Preprocessing:

Boresight shadow map

Radiometric correction, de-striping, saturation masking

Processing: Stage 1

Atmospheric correction SVC method SVC site Image AOI site Image

F1 F2

F3 F4

Stage 2

Stage 3

Nonnegative Matrix Factorization

Spectral Classification Product

Image segmentation combined with a Markov

random field model under a Bayesian framework

Stage 4

Thematic Map

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

396

whitewashed wood board, which has been scanned

simultaneously with the study area (building facade).

The proposed classification method (Brook et al.,

2011) is in four steps (Figure 1): SVM's (Support

Vector Machine) probabilistic map; data reduction;

unmixing; classification.

In a first step a general (coarse) classification is

performed. Each “pure” pixel is assigned to a class

according to a predefined threshold of a probabilistic

output of a support vector machine (SVM)

algorithm, or is labeled as unclassified (Villa et al.,

2011). The unclassified pixels might be associated

with mixed spectra pixels, thus their classification is

addressed to unmixing methods in order to obtain

the abundance fraction of each endmember class.

Prior to this step, a second step is applied, where the

spectral data is reduced by several selected

algorithms. This step is proven to enhance overall

performance of the forthcoming spectral models.

Finally, in the fourth stage the spectral model for

quantitative mapping is applied on the unclassified

pixels of airborne hyperspectral imagery by

considering the preliminary results.

In the first stage, a simple scheme one-class

SVM “weighted centroid” (Schölkopf, 2001) was

applied. For a supervised learning system, each data

instance in the training set consists of a class and

several features. The goal of SVM is to produce a

model that can predict the target value. The

classification procedure is carried out by SVM’s

supervised learning algorithms (Vapnik, 1998).

Given a set of training vectors SVM learns a linear

decision boundary to discriminate between classes.

The results are using SVM’s probability values as a

classification procedure (Villa et al., 2011).

According to this method pixels with a probability

higher than a predefined threshold are related to a

single class. However, pixels with lower probability

are considered to represent mixed pixels, which are

temporary unclassified. We suggest using a kernel in

conjunction with an SVM, as well. The input spectra

are mapped into a high-dimensional vector space

where the coordinates are given by spectral features.

The SVM produces a linear decision boundary in

this high-dimensional feature space, and test

sequences are classified based on whether they map

to the positive or negative side of the boundary.

This approach combines SVM with spectral

Kernel supported and supervised by general prior

knowledge of the endmembers and the ground site.

The method enables direct computation of Kernel

values without calculating feature vectors, which

saves and minimizes computation time. The features

used by Kernel are assumed to be the set of all

possible pure endmembers of a fixed k-length. In the

linearly separable case, the hard margin SVM

determines the hyper-plane that separates the data

and maximizes the distance to the nearest training

points. In the real-world case, training sets are

usually not linearly separable, and we must modify

the SVM optimization process. We suppose that the

training set could be formulated as a sequential

vector space called feature space. The output of the

SVM is a set of weights that solve the dual

optimization problem. It is not a trivial task to

determine the threshold for classification decision of

pure or mixed pixels. The test set classification is

done by moving a k-length sliding window across

input vectors, searching for the current k-length in

the look-up table, and increasing the classifier

threshold by the associated coefficient.

The input variables in terms of absorption

features were reduced through a sequential forward

selection (SFS) algorithm (Whitney, 1971) in the

second stage of the suggested classification method.

This SFS starts with the inclusion of feature sets one

by one to minimize the prediction error of a linear

regression model. This stage focuses on conditional

exclusion based on feature significance (Pudil et al.,

1994). The tuning of decision thresholds is very

difficult during the processing and verification

stages. This type of uncertainty is a well-known fact

in the domain. Therefore, an additional orthogonal

forward selection algorithm incorporates the Gram–

Schmidt transform (Chen et al., 1989) is proposed.

The orthogonal Gram–Schmidt transform space

can be associated with the same number of input

variables of the measurement space (Chen et al.,

1989). The first step of this algorithm considers all

wavelengths as variables and calculates the

Mahalanobis distance. The variable that yields

maximum class separation is added to the feature

subset. The next step is to continue classifying all

remaining variables by calculating the Mahalanobis

distance and adding the maximum separated classes

to the feature subset. Thus, the algorithm reduces

redundancy. The main drawback of SFS is that

feature selection is permanent and it might lead to

redundant features. The main disadvantage of

Gram–Schmidt transform is the demand for more

computations due to the orthogonal decomposition.

Nevertheless, in the present study, the joined subset

selection algorithm reduced the original data from

198 to 7-24 significant features (wavelength).

The nonnegative matrix factorization (NMF) was

applied on the data provided by the SFS feature-

selection model as an unmixing method suggested in

the third stage (Lee and Seung, 2001). This

FUSION OF OPTICAL AND THERMAL IMAGERY AND LIDAR DATA FOR APPLICATION TO 3-D URBAN

ENVIRONMENT - Pattern Recognition Applications in Remotely Sensed Hyperspectral Image Analysis

397

algorithm search for the pure endmembers and the

unmixing by factorizing a matrix subject to positive

constraints based on gradient optimization and

Euclidean norm designation (Robila and Maciak,

2006).

In the present study, the algorithm was generated

to start with a random linear transform on the

nonnegative data. The algorithm is continuously

computing scalar factors that are chosen to produce

the “best” intermediate pure endmembers and the

unmixing. At each step of the algorithm the pure

endmembers and the unmixing remains positive. In

the proposed scheme the scalar factors were

computed by the derivative of the objective function

on the nonnegative source. The main drawbacks of

this method are computational complexity and

significant computation times; it is because each

iteration needs a new nonnegative source and a new

linear transform. Overall, to compute the new

updated nonnegative source, the algorithm requires a

number of scalar factors that are inspected for the

current iteration. The computation of linear

transform considered in the same manner. The

complexity factors are averaged by numbers of

internal iterations. Lin (Lin, 2007) suggests

computing scalar factors independent of each other

at each iteration, which should be based on the

values obtained in the previous iteration. Rabila and

Lukasz (Rabila and Maciak, 2009) show that the

initial choices of factors (0.0001, 0.001, 0.01, 0.1, 1)

and average number of iterations does not have a

significant impact on the running times and does not

affect the convergence.

The final stage is a method for image

segmentation/classification combined with a Markov

random field (MRF) model under Bayesian

framework. The most common way of incorporating

spatial correlations into a classification process is to

use MRF (Yang & Jiang, 2003) as a priori models.

The MRF is a conditional probability model, where

the probability of a voxel depends on its

neighbourhood. Generally, MRF is a stochastic

process that specifies the local characteristics of an

image and is combined with the given data to

reconstruct the true image. Moreover, MRF is

usually used to obtain the prior distribution for the

Bayesian estimation and formulate the labelling

problem. The prior contextual information of MRF

is a powerful method for classifying spatial

continuity as well as specific patterns and features

providing useful and unique information for the final

thematic map.

The here presented MRF is based on 8-

neighbourhood isotropic model, which does not

favour a particular orientation with equal potential

function for cliques 1-4 and 5-8. The final solution is

obtained by minimizing an energy function, where

deterministic relaxation (Chou and Brown, 1990) is

used.

The potential function for a clique is the

weighted sum of the candidate functions: Gaussian

model and Huber model (Bouman and Sauer, 1993).

This function stabilizes the solution of the problem

by suggesting an efficient optimization method. The

functions are compared by training the parameters of

each model separately on the data.

Since different simultaneously propagating

regions are considered, an extension of the level-set

global to local approach is suggested, while allowing

the propagation speed to depend on the respective

region label. Thus, the performance strongly

depends on the description of the label content. For

that purpose, a statistical approach, where the

number of labels is assumed to be known, is

adopted. Pattern analysis techniques for the

identification of the corresponding models are

further used.

The global map of labels is obtained using

statistical tests. These tests classify points with high

confidence. The probability of classification error is

set to a small value. At first, all pixels are classified

according to their distance from the different labels.

The distribution of the data in a window centered at

each site is approximated. Then the Euclidian

distances from this distribution to the features of

each label are computed and assigned to the local

region.

The validation of the thematic maps is performed

by comparing ground truth and image reflectance

data of the selected targets. The ten well-known

targets (areas of approximately 30-40 pixels) were

spectrally measured (using ASD SpecPro) and

documented. The overall accuracy for the Ma'alot

Tarshiha images (Figure 2) is 96.8 and for the

Qalansawe images (Figure 3) is 97.4.

The suggested pattern analysis is based on the

Graph-theoretic algorithm, which integrates the

thematic information to the reconstructed patterns of

buildings and roads. At first, the constrained

Delaunay triangulation (CDT) is performed. The

CDT is refined by two objects, which are connected

by edges of the triangles; the proximity relationship

between buildings and between buildings and roads

are explicitly modelled by this structure. Based on

the proximity relationship between buildings, an

initial graph is generated from which the pattern

recognition based on Minimum Spanning Tree

(MST) is automatically derived (Steele, 2002). Here

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

398

Figure 2: (a) Thematic map (b) Spectral library of Ma’alot Tarshiha endmembers.

Figure 3: (a) Thematic map (b) Spectral library of Qalansawe endmembers.

all the edges are actually weighted based on the

proximity between building outlines. This means

that the weights stored in the edges are calculated by

the nearest distances between building outlines.

Next, the wall statistical weighting method

(Duchesne and Bernatchez, 2002) to compute

building orientation is implemented. Second, the

normal direction of a portion of a road is computed

based on the average of all the segments weighted

by lengths. The last calculation is for the shape

index (Duchesne and Bernatchez, 2002).

In the Graph-theoretic algorithm, a spanning tree

of an undirected graph is a tree that contains all

vertices. The weight of a tree is defined as the sum

of the weights of all its constituent shapes (building

features). A MST tree is then a spanning tree whose

weight is the minimum among all spanning trees.

Since a graph may not be connected it has a union of

minimum spanning trees for its connected

components. In this work, Prim’s algorithm is

implemented to derive MST from initial graph.

The basic idea of the detection is align-along-

road patterns that are traced on a path from the

pruned MST and the buildings, yet the path should

be close enough to a nearby road. Aligned road is

firstly checked using the information stored as a

result of constructing refined CDT. If buildings are

connected by the same road, then the tracing

proceeds. The characterization of align-along-road

building patterns is executed by applying MST to

spectral class, spacing, size, shape, and distance to

the aligned road.

2.3.2 Thermal Imagery

Atmospheric correction is a key processing step for

extracting information from thermal infrared

imagery. The ground-leaving radiance combined

with the temperature emissivity separation (TES)

algorithm are generated and supplied to in-scene

atmospheric compensation ISAC (Young et al.,

2002). The temperature of three prior selected

ground truth targets (water, sand and soil) was

continuously measured by installed thermocouples.

The generated atmospheric data cube is used as an

input to a temperature emissivity separation

algorithm (normalized emissivity method). The pre-

processing methodology is presented in Figure 4.

The proposed thermal classification method

follows the same four stages of data processing

(SVM's probabilistic map; data reduction; umnixing;

classification). The validation of the thematic maps

(Figure 5A and 6A) is performed by comparing

Figure 4: Flow chart scheme of the thermal data pre-

processing.

0.2

0.4

0.6

0.8

0.45 0.95 1.45 1.95

Reflectance

Wavel en gth (µm)

Ma'alot Tarshiha Endmembers

Red Tile Roof Asphalt

Vegetation Conc rete Floo ring

Whitewashed Co c nrete Roof Bare Soil

Metal

0.2

0.4

0.6

0.8

0.45 0.95 1.45 1.95

Reflectance

Wav elength (µ m)

Qalansawe Endmembers

Asphalt Concrete Bare Soil Vegetation

Airborne Thermal Ground ThermalInput Images:

Preprocessing:

Radiometric correction by system operator

Atmospheric correction

Temperature Image

Emissivity Image

Data Processing

in four stages

FUSION OF OPTICAL AND THERMAL IMAGERY AND LIDAR DATA FOR APPLICATION TO 3-D URBAN

ENVIRONMENT - Pattern Recognition Applications in Remotely Sensed Hyperspectral Image Analysis

399

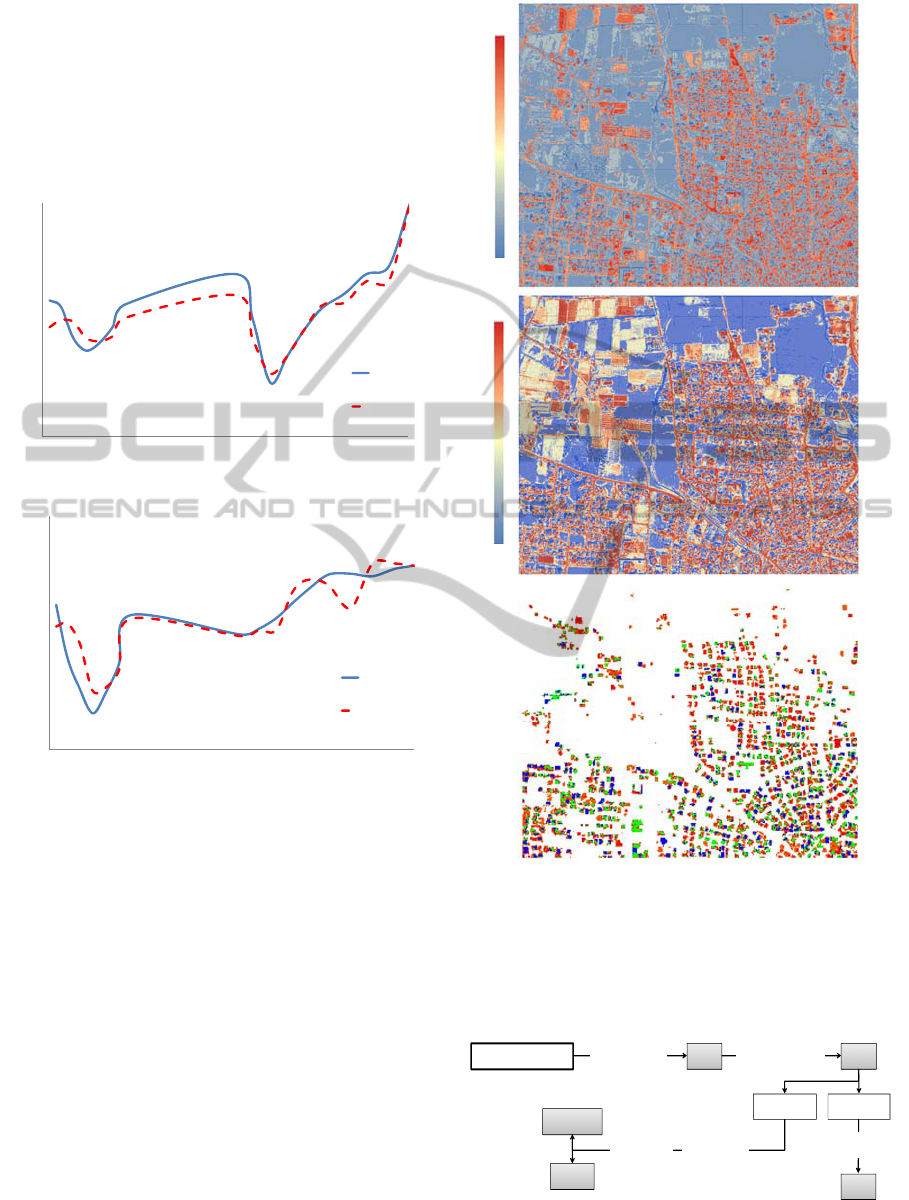
ground truth and image emissivity data. The four

targets (concrete, bare soil, bitumen and tile roof)

were measured and documented. The resulting

emissivity signatures are in good agreement with

ground-truth data (two examples in Figure 5). The

results presented here confirm the robustness and

stability of the suggested method.

Figure 5: Emissivity calculated from the thermal radiance.

A is a tile roof signature in Ma'alot Tarshicha campaign

and B is a bitumen (asphalt road) in Qalansawe campaign.

Figure 6 shows three images for Qalansawe

campaign: a. is the airborne radiance image (3.8µm),

b. is the emissivity image and c. is the thematic map

of concrete.

2.3.3 LiDAR Data

LiDAR data provide precise information about the

geometrical properties of the surfaces and can reflect

the different shapes and formations in the complex

urban environment. The point cloud (irregularly

spaced points) was interpolated into the digital

surface model (DSM) by applying the Kriging

technique (Sacks et al., 1989).

The surface analysis (Figure 7) is first

represented as a DEM (digital elevation model) of

Figure 6: Qalansawe campaign: A. is the airborne radiance

image, B. is the emissivity image and C. is the thematic

map of concrete (4 detected classes).

the scanned scene, where data are separated into on-

terrain and off-terrain points (Masaharu and

Ohtsubo, 2002).

Figure 7: Flow chart scheme of the LiDAR data

processing.

0.9

0.92

0.94

0.96

0.98

35791113

Emissivity

Wavelength (µm)

Tile Roof

הרדיס1

הרדיס2

Image

Ground

Truth

0.84

0.86

0.88

0.9

0.92

0.94

0.96

0.98

3579111

Emissivity

Wavelen

(µ

)

Bitumen

הרדיס

Image

Ground

Truth

Low

High

Low

High

LiDAR point cloud DSM DEM

on-terrainoff-terrain

DTM

Buildings

Roads

interpolation spatial analysis

filters

feature

extraction

geometric

algorithms

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

400

The DTM (digital terrain model) was created by

a morphological scale-opening filter; using square

structural elements (Rottensteiner et al., 2003) for

the on-terrain data. At this stage the roads and

buildings were extracted from the off-terrain data

(Brook et al., 2011).

In relatively flat urban areas, the roads, which

have the same elevation (height) as a bare surface,

can be extracted by arrangement examination. The

simple geometric and topological relations between

streets might be used to improve the consistency of

road extraction. First, the DEM data are used to

obtain candidate roads, sidewalks and parking lots.

Then the road model is established, based on the

continuous network of points which are used to

extract information such as centerline, edge and

width of the road.

The accuracy and correctness of the road

extraction can be evaluated by the completeness of

the detected road network (Cloude et al., 2004). The

comparison between ground truth and detected road

network models is categorized as follows: true

positive (TP), false negative (FN) and false positive

(FP). The accuracy of the extracted road network in

Ma’alot Tarshiha (Figure 8) is 96.2, when TP is 100

(320 m), FN is 0(0 m), and FP is 4 (12.8 m).

Figure 8: The extracted road network in Ma’alot Tarshiha:

A is the LiDAR segmentation, B is the LiDAR

classification, C is the ground truth map.

The building boundary is determined by a

modified convex hull algorithm (Jarvis, 1973) which

classifies the cluster data into boundary

(contour/edge) and non-boundary (inter-shape)

points (Jarvis, 1977). This algorithm can quickly

provide a rough idea of the shape or extent of a point

data set with relatively low computing cost (Wang

and Shan, 2009). Separating points located on

buildings from those on trees and bushes, is a

difficult task (Wang and Shan, 2009). The common

assumption is that the building outlines are separated

from the trees in terms of size and shape. Since laser

beams penetrate the canopy, the data include mixed

information of the surface and under the trees. The

dimensionality learning method, proposed by Wang

and Shan (2009), is estimated by measuring the

slope of the extracted planar surfaces (Figure 9).

Figure 9: The DEM examples: A is a building, B is a tree.

The extracted features are simplified and formed

as a basic framework of the polygon. Yet, the

determined framework is not regular. For that

purpose, the regularization clustering and adjustment

algorithm is executed. This algorithm produces

optimized outlines of convex polygons. At the end

of this procedure two datasets are extracted and

stored: the original feature shapes and the simplified

and regulated feature shapes.

2.3.4 Data Registration - Automatic

Approach

A fully controlled, near-real-time, natural and

realistic monitoring system for an urban

environment is the main objective of this research.

The suggested registration algorithm to achieve this,

is an adapted version of the AIRTop (Figure 10)

algorithm (Brook and Ben-Dor, 2011c).

First, the significant regulated features are

extracted from all input data sets and converted to a

vector format. Since the studied scene has a large

area, regions of interest (ROI) with relatively large

variations are selected. The idea of addressing the

registration problem by applying a global-to-local

level strategy (the whole image is now divided into

regions of interest which are treated as an image)

proves to be an elegant way of speeding up the

whole process, while enhancing the accuracy of the

registration procedure (Chantous et al., 2009). Thus,

we expect this method to greatly reduce false alarms

in the subsequent feature extraction and CP

identification steps (Brook et al., 2011). To select

the distinct areas in the vector data sets, a map of

extracted features is divided into adjacent small

blocks (10% × 10% of original image pixels with no

overlap between blocks). Then, the significant CPs

extraction has been performed by applying the

SURF algorithm (Brown & Lowe, 2002).

First the fast-Hessian corners Detector

(Lindeberg, 2004), which is based on an integral

image, was performed. The Hessian matrix is

responsible for primary image rotation using

principal points, whichare identified as

FUSION OF OPTICAL AND THERMAL IMAGERY AND LIDAR DATA FOR APPLICATION TO 3-D URBAN

ENVIRONMENT - Pattern Recognition Applications in Remotely Sensed Hyperspectral Image Analysis

401

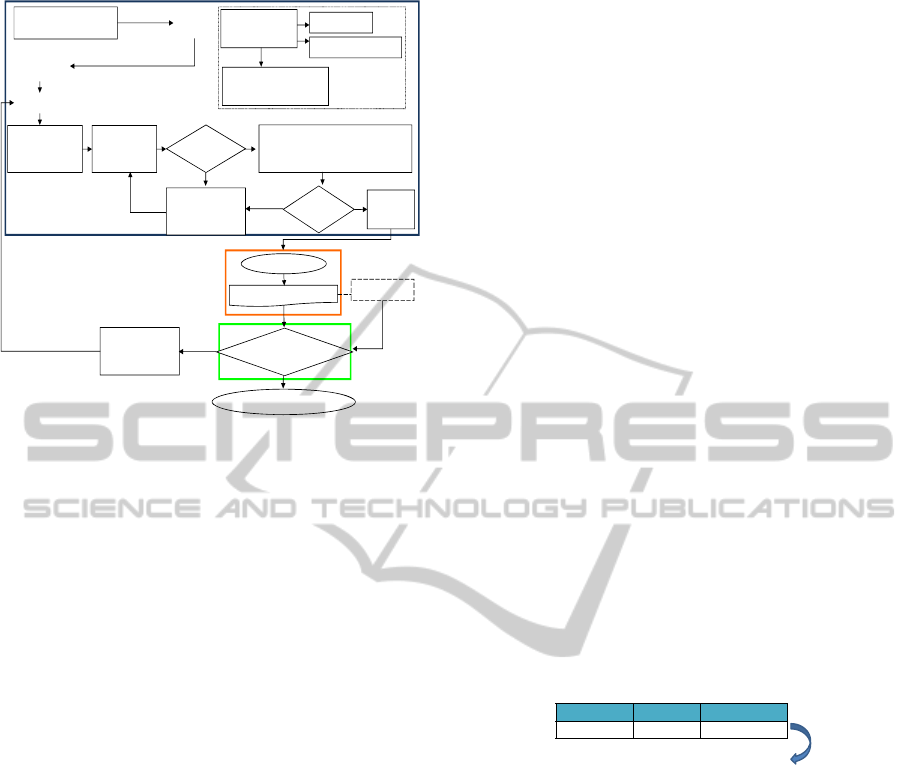
Figure 10: Flow chart of the AIRTop registration

algorithm.

"interesting" potential CPs in the block. The local

feature representing vector is made by a combination

of Haar wavelet coefficients. The values of

dominant directions are defined in relation to the

principal point. As the number of interesting points

tracked within the block is more than the predefined

threshold, the block is selected and considered a

suitable candidate for CPs detection.

The significant features are extracted from all

input data sets. The spatial distribution and

relationship of these features are expressed by

topology rules (one-to-one) and they are converted

to potential CPs by determining a transformation

model between sensed and reference data sets. The

defined rules for a weight-based topological map-

matching (tMM) algorithm manage (Velaga et al.,

2009), transform and resample features of the sensed

georeferenced LiDAR data according to a non-

georeferenced imagery in order to reserve original

raw geometry, dimensionality and imagery matrices

(imagery pixels size and location).

3 URBAN ENVIRONMENT

MODEL

The data fusion application must provide fully

integrated information, both of the classification

products and the context within the scene. In the

proposed model, a complete classification and

identification task consists of subtasks, which have

to operate on material and object characteristic shape

levels provided by an accurately registered database.

Moreover, the final fused and integrated application

should be operated on objects of different sizes and

scales, such as a single building detected within an

urban area or a selected region on a building facade.

The multi-scale and multi-sensor data fusion is

possible with the eCognition procedure (user guide

eCognition, 2003), when the substructures are

archived by a hierarchical network. Thus, each

object is not only identified by its spectral, thermal,

textural, morphological, topological and shape

properties, but also by its unique information linkage

with its actual neighbours (Graph-theoretic

algorithm and topology).

The data are fused by mutual dependencies

within and between objects that create a semantic

network of the scene. To assure high level accuracy

and operational efficiency the input products are

inspected by the basic topological rule, which

obligates that object borders overlay borders of

objects on the next layer. Therefore, the multi-scale

information, which is represented concurrently, can

be related to each other.

One of the most important aspects of

understanding fused data is information about

context, which describes the relationships between

multi-source layers. In human perception, processing

of context information is consciously or sub-

consciously executed. The conceptual information is

integrated into the suggested expert system.

Figure 11: Hierarchical rule-based structure in eCognition.

The expert system is applied on the semantic

network of fuzzy logic (Benz et al., 2004) to

quantify uncertainties and variations of the input

data. This logic establishes the membership function

that defines the relationship between object and its

characteristics (Figure11).

In order to receive meaningful information, the

semantic context has to be determined. For example,

the classification task to identify a roof can be

Fast-Harris

Corner detection

Integral Image

Hassian Approximation

Haar Wavelet Response

Region orientation

SURF

Algorithm

Collect CPs

Initialization:

-Insert features

-Topology building

Matching:

-Linear network

-Transfer match

Unpacking (Topology match checking):

-Feature composition relationship

-Matching pairs

Loop:

Calculation of each

element in pairs

Weigh ts

Hierarchy

RMS

Threshold

Yes

Determine

CP Pair

Test Point Error

(TPE) Threshold

Complete Algorithm

Execute Map-Matching

Trans form

Loop:

Calculation of

lower weight pair

Yes

Preliminary

Detection

Automatic Registration -

Control Point Detection

Primary

Detection

Weight-based Topological Map-matching

ObjectLevelOperation

RoofLevel 1Segmentation

Hierarchical rule-base structure in eCognition:

Roof

• Shape 3-D

• Shape

• Proportions

• Volume 3-D

• Area 2-D

• Diameter 2-D

• Delta H (ground surface - top)

• Material

• VNIR-SWIR thematic class

• Tile

• Bitumen

• Concrete

• Thermal micro – silicates class

• Tile

• Bitumen

• Concrete

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

402

solved by the following approach: A roof is always a

shaped polygon, above the ground level, and with

certain properties (volume, area and diameter). The

different materials and scales distinguish cadastral

categories of a building.

4 3-D URBAN APPLICATION

The interface of the 3-D urban application is based

on a realistic illustration that can be regularly

updated with attribute details and sensor-based

information. The spatial data model is a hierarchical

structure, consisting of elements, which make up

geometries, which in turn compose layers. A

fundamental demand in non-traditional, multi-

sensors and multi-type applications is spatial

indexing. A spatial index, which is a logical index,

provides a mechanism to limit searches based on

spatial criteria (R-tree index).

CityGML is an application based on OGC’s

(open geospatial consortium) GML 3.1. This

application not only represents the graphical

appearance but in particular, it takes care of the

semantic properties (Kolbe et al., 2005), such as the

spectral/thematic properties, and model evaluations.

The 3-D urban application is based on an

integrated data set: spectral models, ground camera

and airborne images, and LiDAR data. This

application offers an advanced methodology by

integrating information into a 5-D data set. The

ability to include an accurate and realistic 3-D

position, quantitative information, thermal properties

and temporal changes is provided by a near-real-

time monitoring system for photogrammetric and

urban planning purposes.

The system requirements are defined to include

geo-spatial planning information and one-to-one

topology. As the requirements consist of

visualization and interactivity with maps and 3-D

scenes, the interface includes 3-D interaction, 2-D

vertical and horizontal interactions and browsers that

contain spectral-temporal information.

The application provides services such as

thematic mapping, and a complete quantitative

review of the building and it's surrounding with

respect to temporal monitoring. The design of the

application shows the possibilities of delivering

integrated information and thus holistic views of

complete urban environments in freeze-frame view

of the spatio-temporal domain.

The self-sufficient levels contribute information

to this integrated application. The first level mainly

supplies integrated airborne data, termed “City 3-D”.

This level introduces the ability for 3-D and 2-D

thematic mapping and spatial quantitative analysis

of urban surface materials. Users are able to analyze

temporal changes in the selected freeze-frame views,

which are equivalent to number of airborne

campaigns and number of available images uploaded

to the database. To reach the next level, the user

must zoom in and focus on the building level.

The second level adjusts on a single building and

is termed “Building Model”. This level contributes

integrated ground and airborne data. The selected

building is isolated from the global building model

replicated by LiDAR and displayed in relative 3-D

scale (matching this particular building). The level

provides two main products: thematic maps and

quantitative evaluation implemented by spectral

models. Both of these products are 3-D freeze-frame

views, which supply an extensive database for

temporal analysis.

The most specific and localized level is the third

level termed “Spectral Model”. To reach this level,

the user is required to select the area of interest

which is a particular position (a patch) such as an

area on a wall. The spatial investigation at this level

is a continuation of the previous level; however, the

data source is a set of spectral models that are

evaluated for spectral in-situ measurements. This

level does not provide any integrated information,

but georeferences the results of spectral models on a

realistic 3-D scale.

5 DISCUSSION

The 3-D urban application satisfies a fundamental

demand for non-traditional, multi-sensor and multi-

type data. The frequent updating and extension

requirement is replaced by integrating the variation

in data formats and types for developing an urban

environment. The main benefit of 3-D modeling and

simulation over traditional 2-D mapping and

analysis is a realistic illustration that can be

regularly updated with attribute details and sensor-

based quantitative information and models.

The proposed application offers a novel

advanced methodology by integrating both imagery

and LiDAR information into a 5-D data set. The

ability to include an accurate and realistic 3-D

position, quantitative spectral information and

temporal changes provides a near-real-time

monitoring system for photogrammetric and urban

planning purposes.

The proposed algorithm for data fusion proved to

be able to integrate several different types of multi-

sensor data, which are additionally dissimilar in

FUSION OF OPTICAL AND THERMAL IMAGERY AND LIDAR DATA FOR APPLICATION TO 3-D URBAN

ENVIRONMENT - Pattern Recognition Applications in Remotely Sensed Hyperspectral Image Analysis

403

rotation, translation, and possible scaling.

The multi-dimensionality (5-D) of the developed

urban environment application provides services

such as thematic mapping, and a complete

quantitative review of the building and its

surroundings. These services are completed by

providing the ability for accurate temporal

monitoring and dynamic changes (changed

detection) observations.

6 CONCLUSIONS

In conclusion, the suggested application may

provide the urban planners, civil engineers and

decision makers with tools to consider quantitative

spectral information and temporal investigation in

the 3-D urban space. It is seamlessly integrating the

multi-sensor, multi-dimensional, multi-scaling and

multi-temporal data into a 5-D operated system. The

application provides a general overview of thematic

maps, and the complete quantitative assessment for

any building and its surroundings in the 3-D natural

environment, as well as, the holistic view of the

urban environment.

REFERENCES

Ameri, B., 2000. Automatic recognition and 3-D

reconstruction of buildings from digital imagery.

Thesis (PhD), University of Stuttgart.

Benz, U. C., Hofmann, P., Willhauck, G., Lingenfelder, I.,

Heynen, M., 2004. Multi-resolution, object-oriented

fuzzy analysis of remote sensing data for GIS-ready

information. ISPRS Journal of Photogrammetry &

Remote Sensing, 58, 239– 258

Bouman, C. and Sauer K., 1993. A generalized Gaussian

image model for edge-preserving map estimation.

IEEE Trans. Image Processing, 2(3), 296-310.

Brown, H., and Lowe, D., 2002. Invariant features from

interest point groups, in BMVC.

Brook, A. and Ben-Dor, E., 2011

. Advantages of

boresight effect in the hyperspectral data analysis.

Remote Sensing, 3 (3), 484-502.

Brook, A. and Ben-Dor, E., 2011

. Supervised vicarious

calibration of hyperspectral remote sensing data.

Remote Sensing of Environment, 115, 1543-1555.

Brook, A. and Ben-Dor, E., 2011

. Automatic registration

of airborne and space-borne images by topology map-

matching with SURF. Remote Sensing, 3, 65-82.

Brook, A., Ben-Dor, E., Richter, R., 2011. Modeling and

monitoring urban built environment via multi-source

integrated and fused remote sensing data. Internatio-

nal Journal of Image and Data Fusion, in press, 1-31.

Carlson, T. N., Dodd, J. K., Benjamin, S. G., and Cooper,

J. N., 1981. Satellite estimation of the surface energy

balance, moisture availability and thermal inertia.

Journal of Applied Meteorology, 20, 67–87.

Chantous, M., Ghosh, S., and Bayoumi, M. A., 2009.

Multi-modal automatic image registration technique

based on complex wavelets. In: Proceedings of the

16th IEEE International Conference on Image Pro-

cessing, Cairo, Egypt, 173-176.

Chen, S., and Billings, S. A., 1989. Recursive prediction

error estimator for nonlinear models. International

Journal of Control, 49, 569-594.

Chou, P., and Brown, C., 1990. The theory and practice of

Bayesian image labeling, Internat. J. Comput., 4, 185–

210.

Cloude, S. P., Kootsookos, P. J., and Rottensteiner, F.,

2004. The automatic extraction of roads from LIDAR

data. In: ISPRS 2004, Istanbul, Turkey.

Conel, J. E., 1969. Infrared Emissivities of Silicates:

Experimental Results and a Cloudy Atmosphere Mo-

del of Spectral Emission from Condensed Particulate

Mediums. Journal of Geophysical Research, 74 (6),

1614-1634.

Donnay, J. P., Barnsley, M. J., and Longley, P. A., 2001.

Remote sensing and urban analysis. In: J. P. Donnay,

M. J. Barnsley and P. A. Longley, eds. Remote

sensing and urban analysis. London and New York:

Taylor and Francis, 3-18.

Duchesne, P., and Bernatchez, L., 2002. AFLPOP: a

computer program for simulated and real population

allocation, based on AFLP data, Mol Ecol Notes, 2,

380–383.

Herold, M., Goldstein, N. C., and Clarke, K. C., 2003. The

spatiotemporal form of urban growth: measurement,

analysis and modeling. Remote Sensing of Envi-

ronment, 86, 286-302.

Herold, M., Couclelis, H., and Clarke, K. C., 2005. The

role of spatial metrics in the analysis and modeling of

land use change. Computers, Environment and Urban

Systems, 29(4), 369-399.

Hunt, G. R. and Vincent, R. K., 1968. The Behaviour of

Spectral Features in the Infrared Emission from

Particulate Surfaces of Various Grain Sizes. Journal of

Geophysical Research, 73(18), 6039-6046.

Jarvis, R. A., 1973. On the identification of the convex

hull of a finite set of points in the plane. Information

Processing Letters, 2, 18-21.

Jarvis, R.

A., 1977. Computing the shape hull of points in

the plane. In: Proceedings of the IEEE Computer

Society Conference Pattern

Recognition and

Image

Processing, 231-241.

Jensen, J. R. and Cowen, D. C., 1999. Remote sensing of

urban/suburban infrastructure and socio-economic

attributes. Photogrammetric Engineering and Remote

Sensing, 65, 611-622.

Juan, G., Martinez, M. and Velasco, R., 2007.

Hyperspectral remote sensing application for semi-

urban areas monitorring. Urban Remote Sensing Joint

Event, 11 (13), 1-5.

Kidder, S. Q. and Wu, H-T., 1987. A multispectral study

of the St. Louis area under snow-covered conditions

using NOAA-7 AVHRR data. Remote Sensing of

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

404

Environment, 22, 159–172.

Kolbe, T. H., Gerhard, G. and Plümer, L., 2005.

CityGML—Interoperable access to 3D city models.

In: International Symposium on Geoinformation for

Disaster Management GI4DM 2005, Delft,

Netherlands, Lecture Notes in Computer Science,

March, 2005.

Lee, D. D., and Seung. H. S., 2001. Algorithms for

nonnegative matrix factorization. In T. G. Dietterich

and V. Tresp, editors, Advances in Neural Information

Processing Systems, volume 13. Proceedings of the

2000 Conference: 556562, The MIT Press.

Lin, C. J., 2007. Projected gradient methods for non-

negative matrix factorization. Neural Computation,

19, 2756-2779.

Lindeberg, T., 2004. Feature detection with automatic

scale selection. International Journal of Computer

Vision, 30, 79-116.

Masaharu, H. and Ohtsubo, K., 2002. A filtering method

of airborne laser scanner data for complex terrain. The

International Archives of Photogrammetry, Remote

Sensing, and Spatial Information Sciences, 15 (3B),

165-169.

Nichol, J. E., 1994. A GIS-based approach to

microclimate monitoring in Singapore’s high-rise

housing estates. Photogrammetric Engineering and

Remote Sensing, 60, 1225–1232.

Nichol, J. E., 1996. High-resolution surface temperature

patterns related to urban morphology in a tropical city:

a satellite-based study. Journal of Applied

Meteorology, 35, 135–146.

Pudil P., Novovicova J., Kittler J., 1994. Floating search

methods in feature selection. Pattern Recognition

Letters, 15, 1119-1125.

Robila, S. A., and Maciak, L. G., 2006. A parallel

unmixing algorithm for hyperspectral images.

Technical report, Center for Imaging and Optics,

Montclair State University.

Roessner, S., Segl, K., Heiden, U. and Kaufmann, H.,

2001. Automated differentiation of urban surfaces

based on airborne hyperspectral imagery. IEEE

Transactions on Geoscience and Remote Sensing, 39

(7), 1525-1532.

Roth, M., Oke, T. R., and Emery, W. J., 1989. Satellite-

derived urban heat islands from three coastal cities and

the utilization of such data in urban climatology. Inter-

national Journal of Remote Sensing, 10, 1699–1720.

Rottensteiner, F., Trinder, J., Clode, S., Kubic, K., 2003.

Building detection using LIDAR data and

multispectral images. In: Proceedings of DICTA,

Sydney, Australia, 673-682.

Rubila S. A., and Maciak L. G., 2009. Considerations on

Parallelizing Nonnegative Matrix Factorization for

Hyperspectral Data Unmiging. Geoscience and

Remote Sensing Letters, IEEE, 6(1), 57-61.

Sacks, J., Welch, W. J., Mitchell, T. J., and Wynn, H. P.,

1989. Design and analysis of computer experiments.

Statistical Science, 4(4), 409–435.

Salisbury, J. W., Hapke B., and Eastes, J. W., 1987.

Usefulness of Weak Bands in Midinfrared Remote

Sensing of Particulate Planetary Surfaces. Journal of

Geophysical Research, 92, pp. 702-710.

Segl, K., Roessner, S., Heiden, U., Kaufman. H., 2003.

Fusion of spectral and shape features for identification

of urban surface cover types using reflective and

thermal hyperspectral data. ISPRS Journal of

Photogrammetry and Remote Sensing, 58, 99-112.

Scholkopf, B., Platt, J. C., Shawe-Taylor, J., Smola, A. J.,

and Williamson, R. C., 2001. Estimating the support

of a high-dimensional distribution. Technical report,

Microsoft Research, MSR-TR, 87-99.

Steele, J. M., 2002. Minimum spanning trees for graphs

with random edge lengths, Mathematics and Computer

Science, 2, 223-245.

Tao, V., 2001. Database-guided automatic inspection of

vertically structured transportation objects from mo-

bile mapping image sequences. In: ISPRS Press, 1401-

1409.UserGuide eCognition, 2003. Website: www.

Definiens_imaging.com.

Vapnik, V., 1998. Statistical learning theory. New York:

Wiley.

Velaga, N. R., Quddus, M. A. and Bristow, A. L., 2009.

Developing an enhanced weight-based topological

map-matching algorithm for intelligent transport sys-

tems. Transportation Research Part C: Emerging Tech-

nologies, 17, 672-683.

Villa, A., Chanussot, J., Benediktsson, J. A., and Jutten,

C., 2011. Spectral Unmixing for the Classification of

Hyperspectral Images at a Finer Spatial Resolution.

IEEE Selected Topics in Signal Processing, 5(3), 521

– 533.

Vukovich, F. M., 1983. An analysis of the ground tem-

perature and reflectivity pattern about St. Louis,

Missouri, using HCMM satellite data. Journal of

Climate and Applied Meteorology, 22, 560–571.

Wang, J., and Shan, J., 2009. Segmentation of LiDAR

point clouds for building extraction. In: ASPRS 2009

Annual Conference, Baltimore, MD.

Whitney A. W., 1971. A direct method of nonparametric

measurement selection. IEEE Transactions on

Computers, 20, 1100-1103.

Yang, F., and Jiang, T., 2003. Pixon-based image

segmentation with Markov random fields, IEEE Trans

Image Process. 12(12):1552-9.

Young, S. J., Johnson, R. B., and Hackwell, J. A., 2002.

An in-scene method for atmospheric compensation of

thermal hyperspectral data. Journal of Geophysical

Research, 107, 20-28.

Zhou, G., 2004. Urban 3D GIS from LiDAR and digital

aerial images. Computers and Geosciences, 30,

345-

353.

FUSION OF OPTICAL AND THERMAL IMAGERY AND LIDAR DATA FOR APPLICATION TO 3-D URBAN

ENVIRONMENT - Pattern Recognition Applications in Remotely Sensed Hyperspectral Image Analysis

405