
CURVATURE-APPROXIMATED ESTIMATION OF REAL-TIME
AMBIENT OCCLUSION
Tomohito Hattori, Hiroyuki Kubo and Shigeo Morishima
Waseda University, Tokyo, Japan
Keywords:
Real-time, Ambient Occlusion, For Game, Curvature.
Abstract:
We present a novel technique for computing ambient occlusion (Akenine-M¨oller et al., 2008) on real-time
graphics hardware. Our method approximates the occlusion for a local illumination model by introducing
curvature-dependent function. Using our method, we are able to acquire occlusion at lower computational cost
than conventional methods such as SSAO (Bavoil et al., 2008). Our method requires a multi-pass algorithm
with the graphics processing unit (GPU). In the first pass curvature is acquired, and in the second pass the
occlusion is computed from the curvature. In the calculating occlusion from the curvature, we approximate
the geometric shape by a quadric surface function, and then obtain a curvature dependent function which is an
approximation of geometric surface. This function depends only on local variables and we are able to calculate
the ambient occlusion for the local illumination model. According to our results, both the computational
and storage costs are sufficiently low for the technique to be applied to current graphics hardware supported
computer games.
1 INTRODUCTION
Currently, a large number of methods such as soft
shadows, subsurface scattering, high-dynamic range
effects, are being applied in real-time graphics appli-
cations.
Ambient occlusion (Akenine-M¨oller et al., 2008)
is one such method which is as a special case of the
obscurances technique. This method was first pre-
sented by Zhukov et al. and popularized by Landis
and Christensen in the movie industry. Ambient oc-
clusion provides a distinctive edge or soft shadow, by
taking account of the attenuation of ambient light due
to the presence of nearby geometrical features. The
method has been used in films as an alternative to
large computational global illumination methods, be-
cause, it can imitate indirect lighting effects such as
global illumination at minimum computational cost.
The ambient occlusion A at a point
~
P with surface
normal~n is given by
A(
~
P,~n) =
1
π
Z
Ω
+
(V(
~
ω,
~
P)⌊
~
ω·~n⌋)dω (1)
Where
~
ω represents random directions from
~
P on the
surface of the unit hemisphere Ω
+
. V(
~
ω,
~
P) is the vis-
ibility function which has the value 0 when no geo-
metrical feature is visible in the direction
~
ω from
~
P,
and the value 1 otherwise.
In the past the ambient light was given by a con-
stant value in many cases. Multiplying the general
ambient term (Phong, 1975) with (1-A(
~
P,~n)) gener-
ates a much better looking result than the constant am-
bient term only. The ambient occlusion solution bears
comparison with the full global illumination solution,
because ambient occlusion is able to approximate the
ambient term attained by analyzing the global behav-
ior of light.
For this reason, ambient occlusion is also now
gaining interest in the game industry. Several ap-
proaches have been applied in 3D games, baking am-
bient occlusion to create texture, ambient occlusion
fields (Kontkanen and Laine, 2005), screen space am-
bient occlusion (Bavoil et al., 2008) and the like.
However, those approaches are based on various
direction sampling and the computational cost to im-
plement them on computer video games is high. We
are able to reduce the computational cost more than
with current ambient occlusion techniques, by intro-
ducing an algorithm which computes the occlusion
from a curvature dependent function.
The basic idea is as follows. We approximate a
geometrical shape at a point
~
P by a curvature depen-
dent function f(
~
P) and we employ the maximum and
minimum principal curvatures as this function’s vari-
268
Hattori T., Kubo H. and Morishima S..
CURVATURE-APPROXIMATED ESTIMATION OF REAL-TIME AMBIENT OCCLUSION.
DOI: 10.5220/0003848402680273
In Proceedings of the International Conference on Computer Graphics Theory and Applications (GRAPP-2012), pages 268-273
ISBN: 978-989-8565-02-0
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Our ambient occlusion sample applied to the Stan-
ford dragon model.
ables. Then comparing f(
~
P) with Ω
+
, we detect an
occluded direction from f(
~
P) at
~
P. In the next sec-
tion we discuss the previous work. The concept of the
curvature dependent ambient occlusion is explained
in Section 3, the curvature estimation in Section 4 and
the implementation in Section 5.
2 PREVIOUS WORK
Ambient occlusion was originally regarded as a sim-
plified case of the obscurances illumination model
(Zhukov et al., 1998), in which the visibility function
contains distance information of the occlusive. In this
method, the obscurance W is given as follows.
W(
~
P,~n) :=
1
π
Z
Ω
+
ρ(d(
~
ω,
~
P)⌊
~
ω·~n⌋)dω (2)
where d(
~
ω,
~
P) refers to the distance of the first inter-
ception along a ray direction
~
ω from
~
P. The function
ρ ?maps the appropriate distance. Especially in the
game industry, there is a great demand for a real-time
ambient occlusion computing technique, and there are
various attractive methods.
Mendez et al. (M´endez et al., 2003) introduced a
real-time computingambient occlusion method which
dynamically updates the obscurance information in
the presence of deforming objects. In a moving scene,
obscurances are re-sampled only in a selected region
of the scene by utilizing temporal coherence. How-
ever, the method requires a huge number of patches
to give high quality contact shadows.
Ambient occlusion has been popularized in pro-
duction rendering (Landis, 2002) and has been
adopted in the movie, television and game industries.
When ambient occlusion is implemented to create
content, it is typically computed on the surface of
each object in a scene and baked on a texture map to
reduce the computational cost in the run-time. How-
ever, a huge number of occlusion maps have to be
prepared for a movie creation, because one occlusion
map of all the objects in each frame is needed. If the
computing time per map is long, huge timing com-
plexity arises. Therefore many derivative methods
of ambient occlusion have been suggested and devel-
oped. In this case, the goal is to evaluate equation(1)
on the surface of an object and to implement the am-
bient occlusion speedily.
Bavoil et al. (Bavoil et al., 2008) introduced
screen space ambient occlusion (SSAO) which is a
multi-pass rendering technique using a z-buffer. A z-
buffer is one of the back-buffers that contains normal
vectors and the depth of pixels in the screen space.
In SSAO, the occlusion at a point is computed by the
GPU from this z-buffer. The basic idea is as follows.
The simplified shape of the nearby geometry is de-
tected by the depth and normal vector direction of
one (or two) pixels neighboring the depth buffer. The
Monte-Carlo collision detection of the ambient occlu-
sion is calculated from this shape information. Thus,
Bavoil et al. (Bavoil and Sainz, 2009) introduced a
developed version of SSAO for improving the quality
of the ambient occlusion effect.
SSAO is employed in the computer game industry
more than any other ambient occlusion technique, be-
cause it is easy to implement on graphics hardware,
and requires no precomputing for rendering. De-
spite the merits and superiority of SSAO, it has not
been adopted for real computer games, because the
ray sampling method inevitable with SSAO requires
a large computational cost for current graphics pro-
cessors. Therefore, in the next section, we introduce
a novel method for computing high quality ambient
occlusion at a lower cost than SSAO.
3 CURVATURE DEPENDED
AMBIENT OCCLUSION
Previous real-time ambient occlusion techniques need
a great number of functions due to the Monte-Carlo
collision detection algorithms. Our goal is to com-
pute ambient occlusion by the GPU in real-time and
implement our method at a lower computational cost
than previous works.
For this purpose, we approximate the occlusion at
a point
~
P into a function model which depends on
variables given by local features. A technique fea-
turing local variables only is usually called a local
illumination model as opposed to a global illumina-
tion model. The advantages of the local illumination
CURVATURE-APPROXIMATED ESTIMATION OF REAL-TIME AMBIENT OCCLUSION
269

Table 1: List of used symbols.
Variable meaning
~
P
3D position
~
ω
direction vector
~n normal vector on surface
V(
~
P,
~
ω) visibility function
A(
~
P,~n) ambient occlusion
A(κ
max
,κ
min
) our ambient occlusion
Ω
+
hemisphere area
r radius of hemisphere
κ
1
,κ
2
curvatures
κ
max
,κ
min
maximum, minimum principal
curvatures
model are lower computational cost and the ease with
which it can be implemented on the GPU. In this sec-
tion, we introduce our curvature dependent function
which computes the occlusion at
~
P.
The main features described in this section are as
follows.
• Approximating the shape of a geometrical surface
at point
~
P by a function f(
~
P).
• Obtaining the occlusion at point
~
P by comparing
f(
~
P) with the unit hemisphere Ω
+
.
3.1 Approximation of Geometry
Current ambient occlusion techniques employ ray
tracing algorithms to compute the occlusion at a point
~
P, because the geometric shape is undetectable by
variables at this point. We may regard the geometric
surface at
~
P as a function f(
~
P) and we detect the oc-
clusion by analyzing this function over the unit hemi-
sphere Ω
+
. However it is difficult to identify f(
~
P) by
the variables at
~
P, because the geometric shape can, in
many cases, be very complex and unpredictable. To
analyze this geometrical function easily, we converted
the function f(
~
P) into a Taylor series and considered
only the lower terms in the series to simplify it. Fur-
thermore, we put f(
~
P) in the tangential vector space,
by a coordinate transformation. Then the Taylor ex-
pansion becomes a Maclaurin series.In the tangential
vector space the z axis of the Cartesian coordinates is
normal to the surface.
f(x, y) = f(0) + f
x
(0)x+ f
y
(0)y
+
f
xx
(0)x
2
2!
+ 2
f
xy
(0)xy
2!
+
f
yy
(0)y
2
2!
...(3)
f
x
(x,y) is the first order differentiation of f(x, y) with
respect to x. The x and y axes are in the tangential and
bi-normal vector directions, respectively. The f(0)
is equal to 0 because it is the origin of the coordi-
nates. Both f
x
(0) and f
y
(0) are also equal to 0, be-
cause f(x, y) is tangential plane at (x,y) = (0, 0).
Furthermore f
xx
(0) and f
yy
(0) are the curvatures of
the lines of intersection between the x −z(or y −z)
plane and f (x,y) at (x,y) = (0,0). We define the di-
rection of each curvature as κ
1
and κ
2
. The κ
1
and κ
2
intersect each other. We can transform equation(3) as
follows.
f(x, y) =
κ
1
2
x
2
+ 2
f
xy
(0)xy
2!
+
κ
2
2
y
2
... (4)
Then f
xy
(0) is equal to 0, provided that x and y belong
to the axes in which κ
1
and κ
2
are the maximum and
minimum principal curvatures(κ
max
, κ
min
). Addition-
ally, by removing the higher than second order terms,
we obtain the simplified f(x, y) as follows.
f(x, y) =
1
2
(κ
max
x
2
+ κ
min
y
2
) (5)
This function is a quadric surface function and it de-
pends only on the points x and y and the maximum
and minimum principal curvatures. Therefore, it is
very easy to analyze this function. We regard this
simplified f(x,y) as the geometric shape at point
~
P,
and we analyze this function to obtain the occlusion
at this point. In the next subsection, we analyze this
function on the surface of the unit hemisphere Ω
+
and
acquire a curvature dependent occlusion estimation.
3.2 Approximation of Occlusion
In the previous subsection, we introduced a curvature
dependent function which estimates the geometrical
shape at the point
~
P. We analyze this function along
the surface of the unit hemisphere Ω
+
to estimate the
occlusion at
~
P. Before the estimation, we have to
transform f(x, y) into polar coordinates, as follows.
f(r, θ,φ) :rcosθ =
r
2
2
sin
2
θ(κ
max
cos
2
φ+κ
min
cos
2
φ)
(6)
For the unit hemisphere the radius r is constant, and
the range of θ and φ are (−
π
2
≤ θ ≤
π
2
) and (0 ≤ φ ≤
2π) respectively.
Previous ambient occlusion techniques require
great computational cost because they adopt ray trac-
ing algorithms for collision detection. The Monte-
Carlo ray sampling algorithm needs to sample more
than 16 rays per pixel, to acquire a practical quality.
The reason why ray tracing algorithms are employed
is that it is difficult to detect occlusions from the ge-
ometry shape surrounding
~
P. However, now we have
the shape of the surrounding geometry and the sur-
face of the hemisphere as functions, we are able to use
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
270

Hemisphere area ¼
2
2
2
1
2
1
yxz NN
Surface
0),( PV
&
&
Z
1),( PV
&
&
Z
1),( PV
&
&
Z
Figure 2: The surface of the hemisphere Ω
+
(blue line) and the quadric surface function f(r, θ,φ) (red line). In the occluded
area, the visibility function V(
~
ω,
~
P) is equal to 0, and is 1 otherwise. We will obtain the occluded area by analyzing this figure
estimation.
these analytically to acquire the occlusion. We define
the hemisphere Ω
+
to be centered at the origin of the
tangential space, and the function f(x,y) to be an oc-
clusive geometry. We estimate the visible parts on Ω
+
from origin as in fig(). Then, we obtain the curvature
dependent visibility function V
′
(
~
ω,
~
P) as follows.
V
′
(
~
ω,
~
P) =
(
1 (
1
2
(κ
max
x
′2
+ κ
min
y
′2
) > z
′
)
0(
1
2
(κ
max
x
′2
+ κ
min
y
′2
) ≤ z
′
)
x
′
,y
′
andz
′
refer to the points of intersection between
Ω
+
and f(x, y) =
1
2
(κ
max
x
2
+ κ
min
y
2
). As a result, we
obtain the following occlusion estimation function.
A(κ
max
,κ
min
) =
Z
2π
0
Z
θ
0
r
2
φsinθ
′
dθ
′
dφ (7)
this θ = arccos(
−1±
√
1+ A
2
A
)
(A = R(κ
max
cos
2
φ+ κ
min
sin
2
φ)
This function, depending on curvature alone, is a lo-
cal illumination approximation of occlusion. Adopt-
ing this approximation, we can obtain an ambient oc-
clusion effect at low cost, thus the implementation is
very easy. When we obtain the occlusion from a static
object, we do not need any other process. In this pa-
per, we more simplify equation(8) as follows by using
a symmetry between x and y, because it is difficult to
implement equation(8) for current computer.
A(κ
max
,κ
min
) =
2arccos(
−1±
√
1+(κ
max
+κ
min
)
2
r
2
(κ
max
+κ
min
)
2
)
π
(8)
This is an important update from ”Curvature de-
pended local illumination approximation of ambi-
ent occlusion” (Hattori et al., 2010). In the paper,
we have to adopt some look-up table(LUT) or quite
rough approximated function which ignore physical
property to implement equation(8). Now, using this
equation(8), we are able to implement our ambient oc-
clusion correctly and in real-time. However, our goal
is to compute the ambient occlusion for a deformable
object, so we introduce a real-time curvature comput-
ing technique in the next section.
4 IMPLEMENTATION
In the previous section, we obtained the curvature de-
pendent function for estimating an occlusion at
~
P. By
converting this function using the current rendering
process, we can acquire an ambient occlusion effect
as a local illumination model. However, it is rare for
the curvature to be given by current polygon model
formats, so we have to calculate the curvature in real-
time. In previous works, many real-time estimations
of curvature have been suggested and the methods can
be simply divided into two categories as follows.
• Estimations in the screen space with no pre-
computing.
• Estimations in world space with some pre-
computing.
In our method, we employ the screen space algorithm,
because the purpose of our work is to obtain an am-
bient occlusion effect, at lower cost than in previous
works and by a method that is easy to implement.
It has already been shown that screen space estima-
tion is easy to implement in computer games on cur-
rent graphics hardware. Wesley et al. (Griffin et al.,
2011) introduced real time curvature estimation in the
world space. They employed a programmable geom-
etry shader to detect the normal curvature by analyz-
ing the normal and position vectors of neighboring
polygons. Yu et al. (Yu et al., 2007) applied their
screen space caustics estimation to compute curvature
in real time. They used pre-computed shape infor-
CURVATURE-APPROXIMATED ESTIMATION OF REAL-TIME AMBIENT OCCLUSION
271
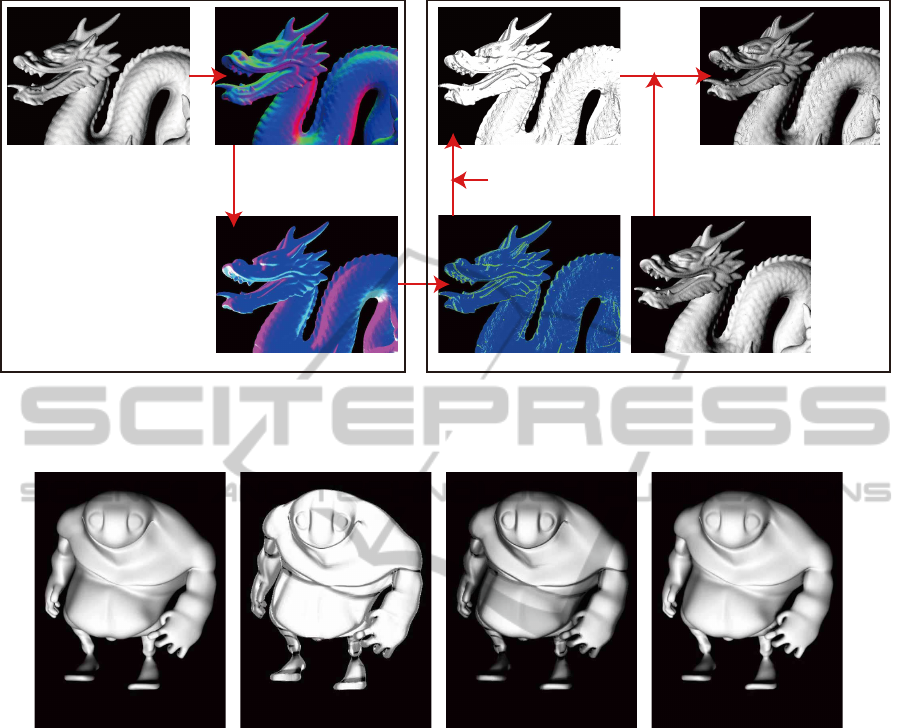
(SBEJFOUBOBMZ[JOH $VSWBUVSFBOBMZ[JOH
0DDMVTJPOFTUJNBUJPO
"U5IF'JSTU3FOEFSJOH1BTT
5IFOPSNBMWFDUPSBOEEFQUI
"U5IF4FDPOE3FOEFSJOH1BTT
0VSPDDMVTJPOGVODUJPO
0UIFS4IBEJOH.FUIPET5IJTJT-BNCFSU
$POWFSUJPO
'JOBMJNBHF
Figure 3: The flow of our implementation.
(a) Lambert. (b) Our method. (c) Our method + Lambert. (d) Lambert + SSAO.
Figure 4: Curvature dependent ambient occlusion images(b)(c) and SSAO(d).
mation to compute curvature with low computational
running cost. Employing these methods we can ac-
quire a greater variety of ambient occlusion effects.
When we adopt Wesleyfs technique, we can obtain
the characteristics of a three-dimensional geometric
shape. In some cases, this is a great advantage, so we
shall be implementing this method in our future work.
5 RESULT AND DISCUSSION
We show a result obtained by employing our method
in Figure(4). (a) shows a Lambert-rendered image,
(b) shows our method, and (c) shows an image com-
posed of (a) and (b). (d) shows the image ren-
dered by SSAO. The speed of rendering a 1280×960
pixel image by applying our method is 60fps and
applying SSAO(16 rays sampling with no blur) is
26fps using an Intel 1.6GHz dual core cpu and a
nVIDIA GeForce 320M machine. The result shows
our method runs 130 percent faster than SSAO. Fur-
thermore, Our method is a local illumination method
to realize a fast run time and easy implementation. It
is extremely easy to implement, and, in addition, by
adopting the curvature dependent method, we can ob-
tain a more detailed occlusion estimate than with the
conventional method using collision detection. The
following figure, Figure (5) shows close up images, in
which we can see the effect of having more detailed
occlusion information.
We can see that even for a fairly small shape
changes in geometry are detected. From these results,
we find that our method is effective for determining
small changes in geometry.
Thus, by adjusting the scale of the curvature, cre-
ators are able to change the strength of the ambient
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
272

(a) Our method. (b) SSAO.
(c) Our method. (d) SSAO.
Figure 5: More closed consideration between our method
and SSAO.
occlusion. The results demonstrate that our method
is easy to implement and runs fast on current graph-
ics hard ware, thus making it effective for rendering
small changes in geometry and adjusting the ambient
occlusion intensity.
6 CONCLUSIONS
In this paper, we introduced a curvature dependent
ambient occlusion estimation algorithm. Our method
approximates the ambient occlusion in a local illumi-
nation model by introducing a curvature-dependent
occlusion estimation function. Since the function is
a local illumination model, we are able to render am-
bient occlusion in real-time, and the proposed method
can be easily implemented. Furthermore, the render-
ing speed is twice as fast as SSAO. Using this method,
smoother, more detailed and equal or better quality
occlusion can be achieved than by using the conven-
tional method (Figure 5), because the curvature is
continuous on the surface. These results demonstrate
that our method is effective for implementing in com-
puter games. Adopting our method, we can reduce
the personnel and computational cost, which would
be beneficial for the game industry.
REFERENCES
Akenine-M¨oller, T., Haines, E., and Hoffman, N. (2008).
Real-Time Rendering 3rd Edition. A. K. Peters, Ltd.,
Natick, MA, USA.
Bavoil, L. and Sainz, M. (2009). Multi-layer dual-
resolution screen-space ambient occlusion. In SIG-
GRAPH 2009: Talks, SIGGRAPH ’09, pages 45:1–
45:1, New York, NY, USA. ACM.
Bavoil, L., Sainz, M., and Dimitrov, R. (2008). Image-
space horizon-based ambient occlusion. In ACM SIG-
GRAPH 2008 talks, SIGGRAPH ’08, pages 22:1–
22:1, New York, NY, USA. ACM.
Griffin, W., Wang, Y., Berrios, D., and Olano, M. (2011).
Gpu curvature estimation on deformable meshes. In
Symposium on Interactive 3D Graphics and Games,
I3D ’11, pages 159–166, New York, NY, USA. ACM.
Hattori, T., Kubo, H., and Morishima, S. (2010). Cur-
vature depended local illumination approximation of
ambient occlusion. In ACM SIGGRAPH 2010 Posters,
SIGGRAPH ’10, pages 122:1–122:1, New York, NY,
USA. ACM.
Kontkanen, J. and Laine, S. (2005). Ambient occlusion
fields. In Proceedings of ACM SIGGRAPH 2005 Sym-
posium on Interactive 3D Graphics and Games, pages
41–48. ACM Press.
Landis, H. (2002). Production-Ready Global Illumination.
In Siggraph Course Notes, volume 16.
M´endez, A., Sbert, M., and Cat´a, J. (2003). Real-time ob-
scurances with color bleeding. In Proceedings of the
19th spring conference on Computer graphics, SCCG
’03, pages 171–176, New York, NY, USA. ACM.
Phong, B.-T. (1975). Illumination for Computer Generated
Pictures. 18(6):311–317.
Yu, X., Li, F., and Yu, J. (2007). Image-space caustics and
curvatures. Computer Graphics and Applications, Pa-
cific Conference on, 0:181–188.
Zhukov, S., Iones, A., and Kronin, G. (1998). An ambient
light illumination model. In Rendering Techniques,
pages 45–56.
CURVATURE-APPROXIMATED ESTIMATION OF REAL-TIME AMBIENT OCCLUSION
273
