PATCHWORK TERRAINS

Luigi Rocca, Daniele Panozzo and Enrico Puppo

DISI, University of Genoa, Via Dodecaneso 35, Genoa, Italy

Keywords:

Terrain Modeling, Multiresolution Modeling, Terrain Rendering.

Abstract:

We present a radically new method for the management, multi-resolution representation and rendering of

large terrain databases. Our method has two main beneﬁts: it provides a C

representation of terrain, with k

depending on the type of base patches; and it supports efﬁcient updates of the database as new data come in.

We assume terrain data to come as a collection of regularly sampled overlapping grids, with arbitrary spacing

and orientation. A multi-resolution model is built and updated dynamically off-line from such grids, which

can be queried on-line to obtain a suitable collection of patches to cover a given domain with a given, possibly

view-dependent, level of detail. Patches are combined to obtain a C

surface. The whole framework can is

designed to take advantage of the parallel computing power of modern GPUs.

1 INTRODUCTION

Real time rendering of huge terrain datasets is a chal-

lenging task, especially for virtual globes like Google

Earth and Microsoft Virtual Earth, which may need to

manage terabytes of data. Terrains are usually repre-

sented as Digital Elevation Maps (DEMs) consisting

of collections of grids, which may have different res-

olutions and different orientations.

Figure 1: A view-dependent query executed on the Puget

Sound Dataset with an on-screen error of one pixel. The

different colors represent patches of different sizes.

In order to support interactive rendering, manip-

ulation and computation, it is necessary to adopt ap-

proaches that can rapidly fetch a suitable subset of

relevant data for the problem at hand. Such a releva-

nt subset is usually deﬁned in terms of both spatial

domain and resolution. Besides view-dependent ter-

rain rendering, speciﬁc GIS applications such as anal-

yses in hydrography, land use, road planning, etc.,

require to handle data at different resolutions.To ef-

ﬁciently support such tasks, a model featuring Con-

tinuous Level Of Detail (CLOD) is thus necessary.

At the best of our knowledge, all CLOD models in

the literature not only require to pre-process the input

datasets, but also the data structures they use cannot

be updated dynamically with new data (Pajarola and

Gobbetti, 2007).

In this paper, we present an approach to CLOD

terrain modeling that is radically different from previ-

ous literature. Its salient features can be summarized

as follows:

1. Our method produces on-line a compact C

rep-

resentation of terrain at the desired accuracy over

a given domain. This representation consists of

a collection of rectangular patches, of different

sizes and orientations, which locally approximate

different zones of terrain at different accuracies.

Patches can freely overlap and they are blended

to obtain a single C

function. See Figure 1. The

degree of smoothness k can be selected depending

on application requirements.

2. Starting from the input DEMs, we produce a large

collection of patches of different sizes and accura-

cies, and we store them in a spatial data structure

indexing a three-dimensional space, having two

dimensions for the spatial domain, and a third di-

Rocca L., Panozzo D. and Puppo E..

PATCHWORK TERRAINS.

DOI: 10.5220/0003848500670076

In Proceedings of the International Conference on Computer Graphics Theory and Applications (GRAPP-2012), pages 67-76

ISBN: 978-989-8565-02-0

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

mension for the approximation error. Every patch

is represented as an upright box: its basis corre-

sponds to the domain covered by the patch; its

height corresponds to the range of accuracies for

which the patch is relevant. We optimize the range

of accuracies spanned by each patch, so that the

number of patches used to represent a given LOD

is minimized. Independent insertion of patches

in the spatial index can be performed easily and

efﬁciently, and the result is order independent,

thus dynamic maintenance of the database is sup-

ported.

3. Spatial queries are executed by ﬁnding the set

of boxes that intersect a user-deﬁned surface in

the space deﬁned above, depending on the de-

sired LOD. Such a surface may be freely de-

ﬁned according to user’s needs, thus supporting

space culling and CLOD altogether. Incremental

queries are possible, so that efﬁcient transfer of

patches to the GPU is supported: if the result of

a query differs only slightly from the result of the

previous one, it is sufﬁcient to transfer to the GPU

just the new patches that come in, together with

the identiﬁers of patches to be discarded.

4. The GPU can directly sample this representation

to produce an adaptive (possibly view-dependent)

tessellation with arbitrary connectivity.

This paper describes the general framework,

alongside with two proof-of-concept implementations

of our method. The ﬁrst implementation is tailored for

real time rendering: it provides a C

representation

that can be efﬁciently sampled in real-time. This rep-

resentation can be evaluated efﬁciently in parallel and

it is suitable for a GPU implementation. We present

results obtained with our CPU implementation, which

is already able to support real time rendering (25 fps)

on a moderately large dataset (about 256M points)

with an error of one pixel in screen space. The sec-

ond implementation is focused on quality and can be

used for common GIS tasks, such as analyses in hy-

drography, land use, road planning, etc.: it provides a

smooth C

representation that can support computa-

tions on terrain using continuous calculus. Both im-

plementations support CLOD queries.

2 RELATED WORK

Overall, known approaches to terrain modeling and

rendering can be subdivided in the four categories re-

viewed in the following. The ﬁrst category is bet-

ter suited for modeling purposes, while the other

three categories are speciﬁcally designed for render-

ing. Our proposal belongs to none of them, and it can

be tailored for both rendering, and other GIS tasks,

with small modiﬁcations to a common framework.

CLOD Reﬁnement in CPU. CLOD reﬁnement

methods produce triangle meshes that approximate

the terrain according to LOD parameters that can vary

over the domain (possibly depending on screen or

world space error). They are mostly used for mod-

eling and processing purposes, since they provide an

explicit representation, with the desired trade-off be-

tween accuracy and complexity. Recent surveys on

CLOD reﬁnement methods can be found in (Pajarola

and Gobbetti, 2007; Weiss and De Floriani, 2010).

Cluster Triangulations. Recent GPUs are able to

render many millions of triangles per second, so the

CPU may spend only a few instructions per triangle

in order to prepare data to be rendered in real-time.

This fact has led to the development of methods that

cluster triangles in a preprocessing steps, possibly at

different resolutions, which are then passed to the

GPU and rendered in batches. The rendering prim-

itive is not anymore a single triangle, but rather a tri-

angle strip encoding a large zone of terrain. The chal-

lenge in these approaches is to stitch different clusters

properly. This is usually achieved in a preprocessing

step that guarantees conformality of extracted meshes

(Cignoni et al., 2003). A survey of these approaches

can also be found in (Pajarola and Gobbetti, 2007).

They are usually meant exclusively for rendering pur-

poses.

Geometry Clipmaps. A different approach has

been presented in (Losasso and Hoppe, 2004), where

Geometry Clipmaps are stored in the GPU mem-

ory, and used to render the part of terrain visible

by the user. As the viewpoint moves, the Geometry

Clipmaps are updated in video memory. Tessellation

is performed directly in the GPU. This method takes

advantage of the intrinsic coherence of height maps

to compress the input, thus reducing the amount of

data that are passed to the GPU. With this method,

very high frame rates can be obtained even for huge

datasets.

GPU Ray-casting. The use of ray-casting for ren-

dering height maps is well studied in the literature,

and different GPU techniques that achieve real-time

frame rates have been developed in recent years. In

(Carr et al., 2006), a method to render meshes rep-

resented as Geometry Images is proposed. Follow-

ing a similar approach, speciﬁc methods for real-time

GRAPP 2012 - International Conference on Computer Graphics Theory and Applications

Figure 2: The terrain is covered by a set of regularly sam-

pled grids. Every grid has its own anchor point p, orienta-

tion angle θ and different sample steps for the two axes sX

and sY .

rendering of height maps have been proposed in (Oh

et al., 2006; Tevs et al., 2008). However, all these

methods were not designed to work with large terrain

datasets. In (Dick et al., 2009), a tiling mechanism

is used to support real-time rendering on arbitrarily

large terrains. Ray-casting methods can be used only

for the purpose of rendering, since they do not pro-

duce an explicit multi-resolution representation.

3 PATCHWORK TERRAINS

In this Section, we describe our technique: in Subsec-

tion 3.1, we deﬁne the type of patches we use; then, in

Subsection 3.2, we describe how patches are blended

to form a C

representation of terrain; ﬁnally, in Sub-

section 3.3, we describe the multi-resolution model,

the order-independent algorithm for the dynamic in-

sertion of patches and the spatial queries.

3.1 From Grids to Patches

We assume a two-dimensional global reference sys-

tem Π on which we deﬁne the domain D of the terrain,

where all input grids are placed. A grid is a collection

of regularly sampled height values of terrain. In addi-

tion to the matrix of samples, every grid is deﬁned by

an anchor point, an angle that deﬁnes its orientation,

and grid steps in both directions (see Figure 2). In

the following, we will use the term vertex to denote a

sample point on the grid, and the term cell to denote a

rectangle in D spanned by a 2×2 grid of adjacent ver-

tices. The accuracy of a grid also comes as a datum,

and it is the maximum error made by using the grid to

evaluate the height of any arbitrary point on terrain.

We aim at deﬁning parametric functions that rep-

resent small subsets of vertices of the grid, called

patches. A single patch is deﬁned by an anchor point,

its height, its width, and the coefﬁcients that describe

the parametric function. For the sake of simplicity,

we will consider the height and width of every patch

to be equal, hence the domain of every patch will be

a square. Extension to rectangular patches is trivial.

We consider two types of patches: perfect patches

interpolate the samples of the original terrain; while

approximating patches only provide an approxima-

tion of the original data. We assign an error to each

patch, namely the accuracy ε of the input grid for a

perfect patch; and ε + δ for an approximating patch,

where δ denotes the maximum distance between a

sample in the input grid and its vertical projection to

the patch. We will denote as kernel a rectangular re-

gion inside every patch, while the rest of the patch

will be denoted as its extension zone.

The type of function deﬁning a patch, as well as

the relation between kernel and extension zones, will

vary depending on the application. In Section 4.1 we

provide speciﬁc examples. Our technique, however,

can be used with any kind of parametric function: de-

pending on the application, it may be convenient to

use either a larger collection of simpler patches, or a

smaller collection of more complex patches. The rest

of this section is generic in this respect.

Note that, unlike splines, our patches may freely

overlap, without any ﬁxed regular structure.

3.2 Merging Patches

Given a collection of freely overlapping patches, we

blend them to produce a smooth function that repre-

sents the whole terrain spanned by this collection. In

order to obtain a C

surface that is efﬁcient to eval-

uate, we use a tensor product construction, starting

from the one dimensional, compactly supported ra-

dial basis function deﬁned in (Wendland, 1995). Our

weight function is deﬁned as:

W (x, y,d) =

w(x/d)w(y/d))

−1

w(x/d)w(y/d) dxdy

for x,y ∈ [−d,d] and 0 elsewhere. The 1-dimensional

weight w(t) is a C

function with compact support,

as deﬁned in (Wendland, 1995): see Figure 3 for the

case and Section 4.1 for further details. It is easy

to see that the weight function W has the following

properties:

1. It has compact support in [−1,1] × [−1, 1];

2. Its derivatives up to order k vanish on the bound-

ary of its support;

3. It is C

in [−1,1] × [−1, 1];

4. It has unit volume.

The ﬁrst three conditions guarantee that the

weight function has limited support, while being C

PATCHWORK TERRAINS

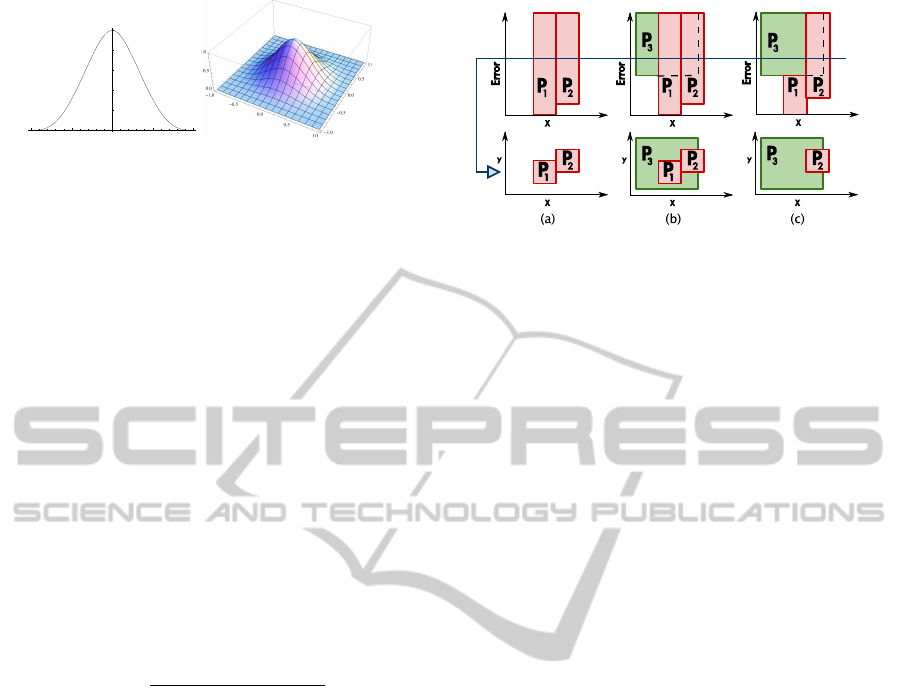
-1.0

-0.5

0.5

1.0

0.2

0.4

0.6

0.8

1.0

(a) (b)

Figure 3: C

weight functions: (a) 1D function w, plot-

ted between -1 and 1. (b) 2D function W , plotted with x,y

between -1 and 1, with the parameter d set to 1.

everywhere. This is extremely important for efﬁ-

ciency reasons, as we will see in the following. Prop-

erty 4 is useful, since it naturally allows smaller (and

more accurate) patches to give a stronger contribution

to the blended surface.

For every patch P, we deﬁne its weight function

(x,y) as a translated and scaled version of W , such

that its support corresponds with the domain of P:

(x,y) = W (|x − P

|,|y − P

|,P

)

with P

and P

the coordinates of the center of P and

the size of P.

A collection of C

patches P

,...,P

placed on

a domain D, such that every point of D is contained in

the kernel of at least one patch, deﬁnes a C

surface

that can be computed using the following formula:

f (x, y) =

∑

i=0

(x,y)W

(x,y)

∑

i=0

(x,y)

(1)

with P

the function associated with patch P

Note that the surface is C

inside D since it is de-

ﬁned at every point as the product of C

functions and

the denominator can never vanish since every point in

D belongs to the interior of the domain of at least one

patch. The summation actually runs only over patches

whose support contains point (x,y), since the weight

function will be zero for all other patches.

At this point, terrain can be described with an un-

structured collection of patches. To use this method

on large datasets, we still miss a technique to efﬁ-

ciently compute this representation at a user-deﬁned

LOD.

3.3 The Multi-resolution Model

We build a multi-resolution model containing many

patches at different LODs, and we provide a simple

and efﬁcient algorithm to extract a minimal set of

patches covering a given region of interest at a given

LOD, possibly variable over the domain.

We deﬁne a 3D space, called the LOD space, in

which two axes coincide with those of the global ref-

Figure 4: Boxes of patches in LOD space, with a cut shown

by the blue line: (a) Two independent patches P

and P

; (b)

A third patch P

is added: patch P

becomes redundant for

the given cut; (c) P

is shortened to obtain a minimal set of

patches for every cut of the spatial index.

erence system Π, while the third axis is related to ap-

proximation error. For simplicity, we will set a maxi-

mum allowed error, so that LOD space is bounded in

the error dimension. In this space, every patch will be

represented as an upright box (i.e., a parallelepiped),

having its basis corresponding to the spatial domain

of the patch, and its height corresponding to the range

of approximation errors, for which the patch is rel-

evant. The bottom of the box will be placed at the

approximation error of the patch, while its top will be

set to a larger error, depending on its interaction with

overlapping boxes, as explained in the following.

In this section, patches will be always treated as

boxes, disregarding their associated functions. We

will consider open boxes, so that two boxes sharing

a face are not intersecting. For a box B, we will de-

note as B.min and B.max its corners with minimal and

maximal coordinates, respectively. Furthermore for a

point p in LOD space, we will denote its three coor-

dinates as p.x, p.y and p.z.

Given a collection of patches embedded in LOD

space, a view of terrain at a constant error e can be

extracted by gathering all boxes that intersect the hor-

izontal plane z = e. More complex queries, which

may concern a region of interest as well as variable

LOD, can be obtained by cutting the LOD space with

trimmed surfaces instead of planes.

To informally describe our approach, let us con-

sider the examples depicted in Figure 4. Figure

4(a) shows two non-overlapping patches embedded

in LOD space: P

is a perfect patch with zero er-

ror, and its box extends from zero to maximum error

in the LOD space. This means that P

will be used

to approximate its corresponding part of terrain at all

LODs. On the contrary, patch P

is an approximating

patch: it has its bottom set at its approximation error,

while its top is again set at maximum error. Patch P

will be used to represent its part of terrain at any er-

ror larger or equal than its bottom, while it will not be

GRAPP 2012 - International Conference on Computer Graphics Theory and Applications

used at ﬁner LODs.

In Figure 4(b), a larger patch P

is added to our

collection, which has a larger error than P

and P

and

also it completely covers P

. A cut at an error larger

than the error of P

would extract all three patches,

but P

is in fact redundant, since its portion of terrain

is already represented with sufﬁcient accuracy from

, which also covers a larger domain. In order to

obtain a minimal set of patches, in Figure 4(c) patch

is shortened in LOD space, so that its top touches

the bottom of P

. Note that we cannot shorten P

in a

similar way, because a portion of its spatial domain is

not covered by any other patch.

This simple example leads to a more complete

invariant that patches in LOD space must satisfy to

guarantee that minimal sets are extracted by cuts. We

ﬁrst formally describe this invariant, then we provide

an algorithm that allows us to ﬁll the LOD space in-

crementally, while satisfying it. This algorithm builds

the multi-resolution model and the result is indepen-

dent of the order of insertion of patches. Implementa-

tion will be described later in Section 4.2.

We deﬁne a global order < on patches as follows:

P < P

if the area of P is smaller than the area of P

;

if the two areas are equal, then P < P

if P.min.z >

.min.z, i.e., P is less accurate than P

Since both the spatial extension and the approxi-

mation error of a patch P are ﬁxed, the spatial invari-

ant is only concerned with the top of P, i.e., with its

maximal extension in the error dimension.

Patch Invariant. A patch P must not intersect any

set of patches, such that the union of their kernels

completely covers the kernel of P, and each patch is

greater than P in the global order <. Also, the patch

P cannot be extended further from above without vi-

olating the previous condition.

In other words, this invariant states that a patch is

always necessary to represent terrain at any LOD, in

its whole extension in the error domain, because that

portion of terrain cannot be covered by larger patches.

If all the patches in the model satisfy this property, we

are sure that we will obtain a minimal set of patches

whenever we cut the model with horizontal planes of

the form z = c. The second part of the invariant forces

patches to span all levels of error where their contribu-

tion is useful for terrain representation, thus maximiz-

ing the expressive power of the model. More general

cuts will also extract correct representations in terms

of LOD, but minimality is not guaranteed.

Let us consider inserting a new patch P into a col-

lection of patches that satisfy the invariant. If the new

patch does not satisfy the invariant, we shorten it at its

top. This is done through Algorithm 1 described be-

low. Note that a patch may be completely wiped out

by the shortening process: this just means that it was

redundant. After the insertion of P, only patches that

intersect P may have their invariance property invali-

dated, so we fetch each of them and we either shorten

or remove it, again by Algorithm 1. All this process

is done through Algorithm 2. Shortening patches that

were already in the model does not invalidate invari-

ance of other patches, so no recursion is necessary.

Algorithm 1: cutter(Patch P, SetOfPatches ps).

1: sort ps in ascending order wrt min.z

2: current = {}

3: last = {}

4: for P

∈ ps do

5: if P ¡ P’ then

6: current = current ∪ {P

}

7: if the patches in current cover P then

8: last = P

9: break

10: end if

11: end if

12: end for

13: if not (last == {}) then

14: if last.min.z ¡ P.min.z then

15: Remove P

16: else

17: P.max.z = P

.min.z

18: end if

19: end if

Algorithm 2: add-patch (Patch P).

1: ps = patches that intersect P

2: cutter(P, ps)

3: for P

∈ ps do

4: if P

still intersects P then

5: ps

= patches that intersect P

6: cutter(P

, ps

)

7: end if

8: end for

It is easy to see that all patches in a model built

by inserting one patch at a time through Algorithm 2

satisfy the invariant. We also show that the result is

independent on the order patches were added.

Order Independence. The structure of a model built

by repeated application of Algorithm 2 is independent

of the insertion order of patches.

Proof. The height of the box associated to a patch de-

pends only on the spatial position and minimal error

of the other patches inserted in the spatial index. The

invariant guarantees that all boxes have their maxi-

mum allowed size in the error dimension, with respect

PATCHWORK TERRAINS

to all other patches in the model. Therefore, the ﬁ-

nal result only depends on what patches belong to the

model. 

To summarize, the algorithm shown allows us to

build a spatial data structure that automatically detects

redundant data. Queries are executed by cutting such

structure with planes or surfaces. Extracted patches

are merged, as explained in Section 3.2, to produce

the ﬁnal terrain representation.

This completes the theoretical foundations of our

technique. We discuss the implementation details in

Section 4, while we provide benchmarks and results

in Section 6.

4 IMPLEMENTATION

This section describes a possible implementation of

the general framework presented in Section 3, which

has been kept as simple as possible for the sake of

presentation. In Section 4.1 we describe the construc-

tion of patches, while in Section 4.2 we describe the

implementation of the spatial index.

4.1 Generation of Patches

We describe two types of patches: bilinear patches

provides a C

representation of the terrain that can

be used for rendering purposes; while bicubic patches

provide a C

representation, trading speed for in-

creased terrain quality.

We use patches at different scales, which are

generated from sub-grids of the various levels of a

mipmap of terrain data. Each patch is a rectangle that

covers a set of samples of the terrains. The patch must

represent the terrain it covers, and its size depends on

the density of grid samples. Patches may also cover

mipmaps, thus allowing to represent larger zones of

the terrain with less samples.

For every level of the mipmap, we build a grid of

patches such that the union of their kernels form a

grid on the domain, and the intersection of their ker-

nel is empty. The size of the kernel with respect to the

size of the patch is a parameter controlled by the user,

that we denote σ. Any value 0 < σ < 1 produces a

terrain representation; different values can be used

to trade-off between quality and performance: small

values of σ improve the quality of blending between

patches; conversely, large values reduce the overlap-

ping between different patches, thus improving efﬁ-

ciency, but transition between different patches may

become more abrupt, thus producing artifacts. In our

experiments, we use σ = 0.9.

Bilinear Patches. are formed by a grid of samples

and they are simply produced by bilinear interpola-

tion of values inside every 2x2 sub-grid of samples.

These patches are C

in their domain, and the blend-

ing function we use is obtained by w(t) = (1 − |t|).

Bicubic Patches. are formed by a grid of samples,

as in the case of bilinear patches. To deﬁne a piece-

wise bicubic interpolating function we compute an in-

terpolant bicubic spline with the algorithm described

in (Press et al., 2007). These patches are C

in their

domain, and the blending function we use is w(t) =

(1 − |t|)

(3|t| + 1).

4.2 Spatial Index

The spatial index must support the efﬁcient insertion

and deletion of boxes, as well as spatial queries, as ex-

plained in Section 5.1. An octree would be an obvious

choice, but it turns out to be inefﬁcient, because large

patches are duplicated in many leaves. We propose

here a different data structure that is more efﬁcient

for our particular application.

We build a quadtree over the ﬁrst two dimensions,

storing in every node n (either internal or leaf) the set

of patches that intersect the domain of n. Not all inter-

secting patches are stored, but just the ﬁrst t patches

that have their highest value on the z-axis, and that are

not stored in any ancestor node of n. We use a thresh-

old t of 64 in our experiments. There is no guarantee

that a patch is stored in exactly one node, but in our

experiments a patch is always stored in less than two

nodes on average.

This data structure can be seen as a set of lists of

patches, ordered depending on their highest value on

the z-axis. Such a set is subsequently split into sub-

lists depending on the spatial domain of patches, in

a way similar to Multiple Storage Quadtrees (Samet,

2005). A visit of the tree produces an ordered list of

the patches that depends only on the spatial domain of

the query surface. This list can then be efﬁciently an-

alyzed to retrieve the patches that intersect the query

surface, since it is ordered on a key deﬁned on the

third dimension.

Inserting a new box in the tree is simple. Starting

at the root, a box B is inserted in the node(s) that inter-

sects its spatial domain, if and only if either the num-

ber of patches in such node does not exceed its capac-

ity, or the highest z-value of the new box is larger than

the highest z-value of at least another box in the list at

that node; in the latter case, the box in the list with the

minimum highest z-value is moved downwards in the

tree. Otherwise, the new patch is moved downwards

in the tree.

GRAPP 2012 - International Conference on Computer Graphics Theory and Applications

As explained in Section 3.3, queries are speciﬁed

by a surface in LOD space. The projection of such a

surface in the spatial domain is the region of interest

(ROI) of the query. The z-values of the surface deﬁne

the error tolerance at each point in the ROI. At query

time, the quadtree is traversed top-down, and quad-

rants that intersect the ROI are visited. For each such

quadrant, only boxes that intersect the query surface

are extracted. When a node n is visited, the query is

propagated to lower levels only if the lowest z-value

of the query surfaces inside the domain covered by n

is less than the highest z-value of all boxes in n.

5 EXTENSIONS FOR REAL TIME

TERRAIN RENDERING

In this Section, we discuss in detail how view-

dependent queries can be executed in our framework

(Section 5.1) and how our terrain representation is

sampled to produce the triangle strip representation

used for rendering (Section 5.2).

5.1 View-dependent Queries

A view-dependent query is needed to minimize the

computational effort required to correctly represent

the terrain region of interest. For example, during ren-

dering it is possible to represent with lower resolution

areas that are far from viewer, without introducing vi-

sual artifacts.

In Section 3.3, a uniform query is executed by cut-

ting the LOD space with a plane parallel to the spatial

domain. A view-dependent query is more complex

since it involves cutting the spatial index with a more

complex surface.

In (Lindstrom et al., 1996) a method was proposed

that computes the maximum error in world coordi-

nates that we can tolerate, in order to obtain an error

in screen coordinates smaller than one pixel. Such a

method deﬁnes a surface in LOD space that we could

use to make view-dependent queries in our spatial in-

dex. However, the resulting surface is complex and

the related intersection tests would be expensive. We

use an approximation of such a method that allows us

to cut the spatial index with a plane, which provides

a conservative estimate of the correct cutting surface:

we obtain a surface that is correct in terms of screen

error, while it could be sub-optimal in terms of con-

ciseness).To compute the cutting plane, we ignore the

elevation of the viewer with respect to the position of

the point, obtaining the the following formula:

screen

dλδ

− v

)

+ (e

− v

)

with e being the viewpoint, v the point of the terrain

where we want to compute the error, d the distance

from e to the projection plane, λ the number of pixels

per world coordinate units in the screen xy coordinate

system, δ the error on world coordinate and δ

screen

the

error in pixel.

This plane is reduced to a triangle by clipping

the zones outside the view frustum. The spatial in-

dex is then cut with this triangle, and the intersection

between boxes in the index and the triangle are ef-

ﬁciently computed with the algorithm of (Voorhies,

1992), after an appropriate change of reference sys-

tem has been performed on the box.

5.2 Terrain Tessellation

So far, we have shown how to extract a parametric C

representation of terrain at the desired LOD. To ren-

der the terrain, we rasterize it by imposing a position-

dependent grid on the domain and by evaluating the

parametric surface only at the vertices of such grid.

We produce a grid that has approximately the same

number of samples as the number of pixels on the

screen, and we deﬁne the grid in polar coordinates,

thus obtaining a mesh with a high density of vertices

in the neighborhood of the viewer and with progres-

sively lower densities as we move farther. For the sake

of brevity, we skip the details on the construction of

this grid and we focus on the efﬁcient evaluation of

the view-dependent terrain representation at its ver-

tices.

Let G be a grid on the domain of terrain and let

S be a set of patches extracted from the spatial in-

dex with a view-dependent query. Equation (1) can

be evaluated efﬁciently by observing that the weight

function associated with a patch P is zero for all the

vertices of the grid that lies outside the domain of P.

Thus, for every patch P

, we need to evaluate P

and

just for the vertices of G that lie in the domain of

We have built a two-dimensional spatial index on

the domain on the terrain that contains the position of

all vertices of G and that allows us to rapidly fetch all

vertices contained in the domain of a patch. We use

a uniformly spaced grid in our prototype. Note that

this spatial index has to be built just once, since the

grid depends only on the position of the viewer. At

each frame, we do not move the grid, but we rather

translate and rotate the patches returned by the query

to place the grid in the desired position. By using

this spatial index, we can efﬁciently extract the ver-

tices that lie in every patch and incrementally com-

pute Equation (1).

Since the terrain is represented by a parametric

PATCHWORK TERRAINS

function, it may be also possible to render it efﬁciently

with ray-tracing. We plan to investigate this opportu-

nity as well as other ways to triangulate the parametric

representation of the terrain in our future work.

6 RESULTS

In this Section we present the results obtained with

our prototype implementation on a dataset over the

Puget Sound area in Washington. Experiments were

run on a PC with a 2.67Ghz Core i5 processor

equipped with 4Gb of memory, using a single core.

The dataset is made up of 16,385 × 16,385 vertices at

10 meter horizontal and 0.1 meter vertical resolution

(USGS and The University of Washington, 2011).

Our prototype performs all computation on a single

CPU core and achieves interactive rendering frame

rates. In a ﬂight over the Puget Sound datasets, our

framework obtains an average of 25 fps, producing

320k triangles per frame with an on-screen error of 1

pixel.

As we will show, the majority of time is spent

in the rasterization of terrain, which could be paral-

lelized easily on the GPU. If we disable the rasteri-

zation, our system is able to respond to hundreds of

queries per second. We expect that a GPU implemen-

tation, which will be the focus of our future work, will

be able to obtain interactive frame rates on large ter-

rains with HD quality, while using only a subset of

the cores available on modern GPUs.

Sections 6.1, 6.2, 6.3 and 6.4 present results pro-

duced using bilinear patches. Section 6.5 discusses

the performance when bicubic patches are used.

6.1 Pre-processing time

The preprocessing computations executed by our sys-

tem can be divided in three phases: mipmap genera-

tion, error evaluation and construction of the spatial

index. Table 1 reports our preprocessing times for the

full dataset, and for two scaled versions. Note that

pre-processing is performed online, i.e. it is possible

to add new data to a precomputed dataset without the

need to rebuild it from scratch. This feature is unique

of our method since, at the best of our knowledge, it

is not available in any other work in the literature (Pa-

jarola and Gobbetti, 2007).

In our experiments, each patch covers a grid of

32x32 samples, while its kernel is made of the central

28x28 pixels.

The majority of time is spent on the ﬁrst two

phases, which would be simple to execute in parallel

on multiple cores, unlike the last phase that involves

complex data structures.

6.2 Space Overhead

On average, our multi-resolution model requires

approximately 35% space more than the original

dataset. A breakdown of the space occupied by the

various components of our model is shown in Table

1. The majority of space is taken by the mipmap.

There is a tradeoff between the space occupied by

the multi-resolution model and the size of patches.

Smaller patches increase adaptivity but take more

space since they must be inserted and stored in the

spatial index.

6.3 Uniform Queries

Our system is able to execute 800 uniform queries

per second with a 50m error. Queries with no error

slow down the system to 55 queries per second. Note

that the latter queries return the maximum number of

patches at the highest level of detail possible.

, yielding the highest number of patches an the

most detailed representation possibile, can be exe-

cuted 55 times in a second. Figure 5 shows the re-

sults of three different queries performed with an er-

ror threshold of 5, 20 and 50 meters. Smaller patches

are used to correctly represent ﬁne details, while large

patches are used in ﬂat zones, even with a very low er-

ror threshold. High frequency detail is obviously lost

as error increases.

6.4 View-dependent Queries

A single view-dependent query representing a portion

of terrain 15km long with an on-screen error of one

pixel extracts approximately 250 patches and requires

only 2.5ms. Thus, our system is able to query the

spatial index at very high frame rates, meaning that

the CPU time required for every frame is negligible.

In our prototype, about 95% of the time is spent in

evaluating terrain elevations using Equation 1. This

task is intrinsically parallel, since it can be performed

separately for every vertex of the grid, so we expect

to easily obtain impressive frame rates by demand-

ing to the GPU the evaluation procedure. Figure 6

also shows the number of view-dependent queries per

second executed by our prototype and the number of

extracted patches at different screen error thresholds.

The use of progressive spatial queries could further

increase performance.

In a GPU implementation of our technique, the

query will be executed by the CPU, while the GPU

GRAPP 2012 - International Conference on Computer Graphics Theory and Applications

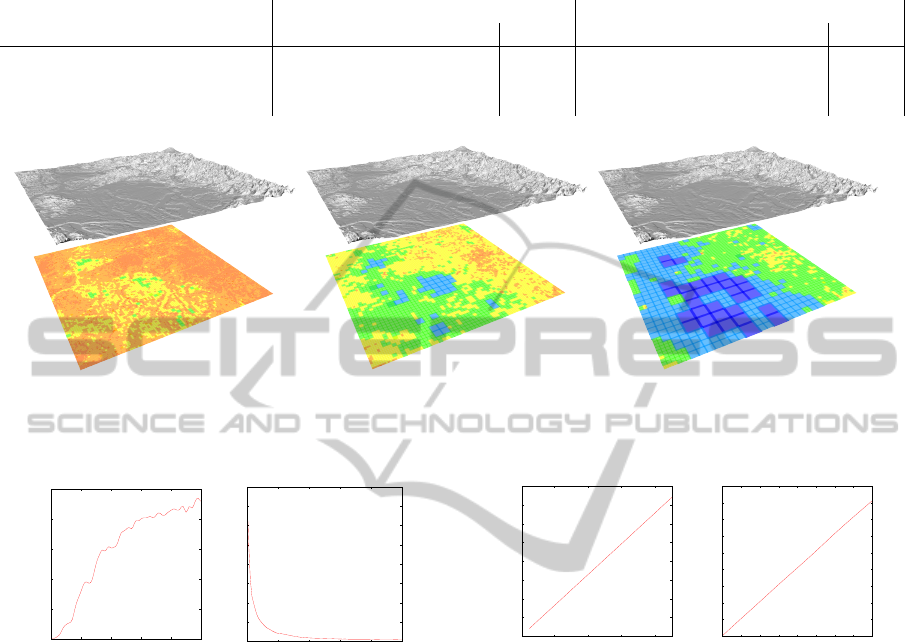
Table 1: Time and space required to preprocess and store the multi-resolution model. From left to right: the time required

to compute the mipmap, to evaluate the error associated with each patch and to build the spatial index; the space required to

store the mipmaps, the patches and the spatial index.

Preprocessing Time Space overhead

Dataset samples Dataset size Mipmap Error Index Total Mipmaps Patches Index Total

1k × 1k 2M 0.1s 0.6s 0.05s 0.75s 702k 18k 12k 732k

4k × 4k 32M 0.9s 10s 0.83s 11.73s 11.2M 301k 202k 11.7M

16k × 16k 512M 12.6s 169s 14.6s 196.2s 179M 4.8M 3.2M 187M

Figure 5: Puget Sound Dataset (16k x 16k samples) rendered with error thresholds of 5, 20 and 50 meters. The colors on the

bottom represent the size of the patch used to approximate the terrain. Blue and cyan corresponds to large patches, used to

approximate ﬂat zones, while red and orange indicates small patches required to represent ﬁne details.

500

1000

1500

2000

2500

3000

0 1 2 3 4 5

Queries per Second

Error (pixels)

(a)

500

1000

1500

2000

2500

3000

3500

4000

0 1 2 3 4 5

Extracted Patches

Error (pixels)

(b)

Figure 6: Number of queries per second (a) and number

of extracted patches (b) while performing view-dependent

queries at different screen error thresholds.

evaluates Equation 1 and rasterizes the resulting ter-

rain. Between different frames, only the difference

between the two queries must be sent to the GPU.

We have simulated the trafﬁc between CPU and GPU,

during a ﬂy over the dataset at different speeds: only a

few kb per frame were required to send the difference

between two queries to the GPU (see Figure 7). Every

patch that has to be sent to the GPU uses 4106 bytes,

while the removal of a patch requires only to transfer

its unique identiﬁer (4 bytes).

6.5 Differences with Bicubic Patches

Changing type of patches inﬂuences differently the

various steps of our framework. The preprocessing

step is slowed down thirty times: this is due to the

200

400

600

800

1000

1200

1400

1600

40 80 120 160

Bandwidth Usage (bytes/frame)

Speed (m/s)

(a)

2000

4000

6000

8000

10000

12000

14000

16000

18000

20000

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

Bandwidth Usage (bytes/frame)

Speed (rad/s)

(b)

Figure 7: During a straight ﬂy over terrain at different

speeds, only a few bytes per frame must be sent to the

GPU (a). A rotation of the viewpoint requires slightly more

bandwidth (b). Both tests were performed with an allowed

screen error of three pixels and every query extracted 70

patches on average, representing a portion of terrain 15km

long.

huge increase of the computational cost required for

the evaluation of the bicubic patches. The construc-

tion of the spatial index is almost unaffected by the

modiﬁcation, since the only information that it needs

is the maximal error associated with every patch. The

space used is similar. The evaluation of the terrain is

greatly slowed down and we could obtain just one fps

with the CPU implementation. While our current im-

plementation can be used just for modeling purposes,

a GPU implementation is required to achieve interac-

tive rendering frame rates with bicubic patches.

PATCHWORK TERRAINS

7 CONCLUDING REMARKS

We have presented a novel technique for represent-

ing and manipulating large terrain datasets. Its main

advantage is the possibility to efﬁciently update the

system with new heterogeneous grids, a character-

istic that is not found in any existing method. The

system automatically detects and removes redundant

data. Furthermore, our technique produces a multi-

resolution C

surface instead of a discrete model. The

actual evaluation of the surface, which is the only

computationally intensive task, can be demanded to

the GPU, while keeping the communication between

CPU and GPU limited. Texture and normal map can

be easily integrated, since they can be associated to

every patch and interpolated, with the same method

used for the height values.

The space overhead required by the multi-

resolution model is approximately the same as the

space used for a mipmap pyramid, thus it is suitable

to be used even with huge terrains. A limitation of

this technique is the lack of a theoretical bound on the

maximum number of patches that may overlap at a

single point of terrain. This can probably be avoided

if we insert additional criteria to the patch invariant

we use for building the spatial index, and it will be

one of the main points of our future work. However,

in our experiments the number of overlapping patches

never exceeded six, and it was four on average.

We have presented results obtained with our CPU

implementation, which is already able to obtain in-

teractive rendering frame rates using a single core on

moderately large terrains. The algorithm for the con-

struction and update of the multi-resolution model, as

well as the query algorithms are efﬁcient and capable

to manage huge datasets.

We are currently working on a GPU implemen-

tation and the most relevant aspects to achieve efﬁ-

ciency are: incremental queries, providing a stream

of differences between patches deﬁning terrain in the

previous and current frame, which can be directly

transferred to the GPU; efﬁcient update of the list of

patches maintained in the GPU; and the strategy for

parallel evaluation and meshing of terrain.

REFERENCES

Carr, N. A., Hoberock, J., Crane, K., and Hart, J. C. (2006).

Fast gpu ray tracing of dynamic meshes using ge-

ometry images. In Gutwin, C. and Mann, S., ed-

itors, Graphics Interface, pages 203–209. Canadian

Human-Computer Communications Society.

Cignoni, P., Ganovelli, F., Gobbetti, E., Marton, F., Pon-

chio, F., and Scopigno, R. (2003). Bdam - batched dy-

namic adaptive meshes for high performance terrain

visualization. Comput. Graph. Forum, 22(3):505–

514.

Dick, C., Kr

uger, J., and Westermann, R. (2009). GPU ray-

casting for scalable terrain rendering. In Proceedings

of Eurographics 2009 - Areas Papers, pages 43–50.

Lindstrom, P., Koller, D., Ribarsky, W., Hodges, L. F.,

Faust, N., and Turner, G. A. (1996). Real-time, con-

tinuous level of detail rendering of height ﬁelds. In

SIGGRAPH ’96: Proceedings of the 23rd annual con-

ference on Computer graphics and interactive tech-

niques, pages 109–118, New York, NY, USA. ACM.

Losasso, F. and Hoppe, H. (2004). Geometry clipmaps:

terrain rendering using nested regular grids. In SIG-

GRAPH ’04: ACM SIGGRAPH 2004 Papers, pages

769–776, New York, NY, USA. ACM.

Oh, K., Ki, H., and Lee, C.-H. (2006). Pyramidal displace-

ment mapping: a gpu based artifacts-free ray tracing

through an image pyramid. In Slater, M., Kitamura,

Y., Tal, A., Amditis, A., and Chrysanthou, Y., editors,

VRST, pages 75–82. ACM.

Pajarola, R. and Gobbetti, E. (2007). Survey of semi-regular

multiresolution models for interactive terrain render-

ing. Vis. Comput., 23(8):583–605.

Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flan-

nery, B. P. (2007). Numerical Recipes 3rd Edition:

The Art of Scientiﬁc Computing. Cambridge Univer-

sity Press, 3 edition.

Samet, H. (2005). Foundations of Multidimensional and

Metric Data Structures (The Morgan Kaufmann Se-

ries in Computer Graphics and Geometric Model-

ing). Morgan Kaufmann Publishers Inc., San Fran-

cisco, CA, USA.

Tevs, A., Ihrke, I., and Seidel, H.-P. (2008). Maximum

mipmaps for fast, accurate, and scalable dynamic

height ﬁeld rendering. In Haines, E. and McGuire,

M., editors, SI3D, pages 183–190. ACM.

USGS and The University of Washing-

ton (2011). Puget sound terrain.

http://www.cc.gatech.edu/projects/large

models/ps.html.

Voorhies, D. (1992). Triangle-cube intersection. Graphics

Gems III, pages 236–239.

Weiss, K. and De Floriani, L. (2010). Simplex and diamond

hierarchies: Models and applications. In Hauser, H.

and Reinhard, E., editors, Eurographics 2010 - State

of the Art Reports, Norrk

oping, Sweden. Eurographics

Association.

Wendland, H. (1995). Piecewise polynomial, positive deﬁ-

nite and compactly supported radial functions of mini-

mal degree. Advances in Computational Mathematics,

4(1):389–396.

GRAPP 2012 - International Conference on Computer Graphics Theory and Applications