
HUMAN AGE ESTIMATION VIA GEOMETRIC
AND TEXTURAL FEATURES
Merve Kilinc
1
and Yusuf Sinan Akgul
2
1
TUBITAK BILGEM UEKAE, Anibal Street, 41470, Gebze, Kocaeli, Turkey
2
GIT Vision Lab
∗
, Department of Computer Engineering, Gebze Institute of Technology, 41400, Kocaeli, Turkey
Keywords:
Age Estimation, Age Classification, Geometric Features, LBP, Gabor, LGBP, Cross Ratio, FGNET, MORPH.
Abstract:
Aging progress of a person is influenced by many factors such as genetics, health, lifestyle, and even weather
conditions. Therefore human age estimation from a face image is a challenging problem. Aging causes
significant variations in facial shape and texture across years. In order to construct a general age classifier,
shape and texture information of human face should be used together. In this paper, we propose a new age
estimation system that uses a number of overlapping age groups and a classifier that combine geometric and
textural facial features. The classifier scoring results are interpolated to produce the estimated age. We tested
many geometric and textural facial features with age group classifiers. Comparative experiments show that the
best performance is obtained using the fusion of Local Gabor Binary Patterns and Geometric features.
1 INTRODUCTION
Human age estimation is one of the most challenging
problems in computer vision and pattern recognition.
Estimating human age from his or her face is a hard
problem not only for the existing computer vision sys-
tems but also for humans in some circumstances.
Aging is not a general progress, different individ-
uals age in different ways. Aging pattern of each
person is determined by many internal and external
factors such as genetics, health, lifestyle, and even
weather conditions (Geng et al., 2007)(Gao and Ai,
2009). In order to achieve successful results in appli-
cations like age estimation or age classification, the
data set that will be used to train the algorithm must
contain all these factors. Therefore, the collection of
training data is another difficulty of research on age
progression and estimation. It is really hard to collect
face images of the same person at different ages and it
is highly important to assign each instance to the right
age class. In order to have a general and qualified ag-
ing pattern that overcomes the negative influences of
individual differences, a complete and accurately la-
beled face aging database is needed.
In spite of these present difficulties, age estimation
can be used in a wide range of smart human-machine
applications, e.g. limiting access to age-appropriate
∗
http://vision.gyte.edu.tr/
Internet or television contents or creating a general
characteristics of a typical customer in a required age
range to be used to develop a marketing strategy. Be-
sides, facial aging is a subproblem in face recogni-
tion, because simulating the appearance of a person
across years may help recognizing his or her face
(Ramanathan and Chellappa, 2006)(Ramanathan and
Chellappa, 2008).
Some earlier work has been reported on different
aspects of age progression and estimation. Kwon and
Lobo (Kwon and Lobo, 1999) proposed an age clas-
sification method that focuses on both the shape and
the wrinkles of human face to classify input images
into only one of the three age groups: babies, young
adults and senior adults. Lanitis (Lanitis et al., 2004)
presented comparative results of different classifiers;
shortest distance classifier, neural network based clas-
sifier and a quadratic function classifier. The face
images are represented by the AAM method and the
best results were obtained when classifiers based on
quadratic function and neural network based classi-
fiers are used. Guo and Fu (Guo et al., 2008) pre-
sented a locally adjusted regressor which uses age
manifold learning to map pixel intensity of the origi-
nal face images into a low dimensional subspace for
the learning and the prediction of the aging patterns.
Yang (Yang and Ai, 2007) used Real AdaBoost algo-
rithm to train a classifier by composing a sequence of
Local Binary Pattern (LBP) features as a representa-
531
Kilinc M. and Sinan Akgul Y..
HUMAN AGE ESTIMATION VIA GEOMETRIC AND TEXTURAL FEATURES.
DOI: 10.5220/0003849005310538
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 531-538
ISBN: 978-989-8565-03-7
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

tion of face texture. Age is classified into only three
periods: child, adult and oldness. Gao (Gao and Ai,
2009) used Gabor features as face representation and
the Linear Discriminant Analysis (LDA) to construct
the age classifier that classifies human faces as baby,
child, adult, or elder people. Images in the training
set are labeled without the age information.
There exists some other work concerning face
recognition with aging variations on human faces. For
example, Burt and Perrett (Burt and Perrett, 1995) de-
scribed a method for the simulation of aging effects
on male faces only by using facial composites which
blend shape and color information. Ramanathan and
Chellappa (Ramanathan and Chellappa, 2006) pro-
posed a craniofacial growth model that characterizes
growth related shape variations observed in human
faces. They used age-based facial measurements and
proportion indices.
Age estimation can be considered either a clas-
sification or a regression problem (Fu et al., 2010).
We can see that for different experiment cases, the
classification based age estimation can be much bet-
ter or much worse than the regression based tech-
niques. Therefore a hybrid approach which combines
the classification and regression methods is the most
effective solution for the age estimation problem.
Although the aging pattern is dissimilar for each
person, individuals belonging to the same age group
share some facial shape and texture similarities. In
this paper, we propose to use overlapping age groups
(Figure 1 and Figure 8) and a classifier that measures
the probability of a given image belonging to each
group. Since our task is to estimate the human age,
we use the interpolated probabilities to reach the final
estimated age.
Figure 1: The overlapping age groups for FG-NET
Database (FGNET, 2010).
We formed our age groups non-uniformly to take
advantage of facial feature developments of different
age phases. During the formative years, facial aging
effects are more pronounced, therefore we partition
the formative years to smaller ranges. For the older
age groups, the ranges get larger because the changes
are smaller compared to the formative age groups.
The age groups are chosen to overlap so that it is pos-
sible to employ an interpolation based technique to
estimate the final age.
For the feature extraction process, first we calcu-
late various ratios of the euclidean distances between
facial points to be used as geometric features. Some
of these distances are calculated in a way that they
are not affected by head poses and perspective dis-
tortion effects of cameras. Second, to extract textural
features, we use face representation techniques such
as LBP, Gabor, Local Gabor Binary Pattern (LGBP)
which are commonly used by the face recognition
community. Then we combine geometric and textu-
ral features and use AdaBoost algorithm to construct
the final classifier. While textural features play an im-
portant role to distinguish age classes between mid-
dle age and older people, geometric features become
more important to classify younger subjects.
The rest of this paper is organized as follows: Sec-
tion 2 describes the proposed overall age estimation
method. Section 3 introduces the geometric features
which are used for the description of the growth re-
lated shape variations for the classification. In Section
4, textural feature extraction methods are presented.
Section 5 shows comparative experimental results in
age estimation and Section 6 provides some conclud-
ing remarks.
2 THE FUSION OF GEOMETRIC
AND TEXTURAL FEATURES
Facial aging effects can be perceived in two main
forms; the first one is the growth related transforma-
tions in facial shape during formative years. The other
is, the textural variations such as wrinkles, creases,
and other related skin artifacts that occur during adult-
hood. Therefore, while some earlier work deal with
only facial texture to construct an age classifier (Gao
and Ai, 2009), some use shape and texture informa-
tion separately to distinguish one age class from the
others (Kwon and Lobo, 1999)(Yang and Ai, 2007).
We tested 8 different classifiers that use different
facial feature vectors. Some of these classifiers use
textural features, some of them use geometric fea-
tures and others use fusion of textural and geometric
features. The overall feature sets of each classifier is
shown in Figure 2.
Before the feature extraction phase of the training,
samples in the training data set are assigned group
labels. Most of the samples are assigned two group
labels because our age groups overlap (Figure 1 and
Figure 8). For the training, first, face boundaries are
automatically detected, and face image patches are
cropped from images in the training dataset. Prior to
feature extraction, all images undergo geometric and
illumination normalization. After the preprocessing
phase, several feature extraction methods are applied
to the normalized face images. 1) Ratios of the dis-
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
532

Figure 2: The overall diagram of the proposed age classification system.
tances between facial landmarks are extracted to be
used as geometric features. 2) The LBP operator is
applied to every pixel of the face image and then re-
sulting values are used as the feature vectors. 3) After
convolving the face image with a range of Gabor fil-
ters, the magnitude responses are used to represent the
Gabor features. 4) The LGBP representations of the
face images are used as LGBP features. In addition
to these extracted features, we combine each textural
feature with geometric features at the feature level to
enhance the representation power of the face image.
After the feature extraction phase, the AdaBoost
learning algorithm (Freund and Schapire, 1996) is
used to model the age classifiers. AdaBoost algorithm
combines the weak classifiers to construct a strong
classifier. In every iteration, it reweighs each instance
according to the output of the classifier. Finally we
obtain 8 distinct classifiers; Classifier 1 uses Geomet-
ric features without cross ratio features, Classifier 2
uses Geometric features, Classifier 3 uses Gabor fea-
tures, Classifier 4 uses the fusion of Geometric and
Gabor features, Classifier 5 uses LBP features, Classi-
fier 6 uses the fusion of Geometric and LBP features,
Classifier 7 uses LGBP features and Classifier 8 uses
the fusion of Geometric and LGBP features.
For testing, an input face image goes through the
same face detection, normalization and feature extrac-
tion phases. Then, the probabilities of each age group
assignment is obtained from the age group classifier.
The probabilities of the highest scoring group and its
two neighbors are used to calculate an interpolated
age value using a weighted average of the three group
centers. Age calculation function is defined as:
age = X
median
+ ((Y
median
− X
median
)/2)P
y
+ ((Z
median
− X
median
)/2)P
z
(1)
where X
median
, Y
median
and Z
median
are the median age
values of the age classes with the highest probabil-
ities respectively. In the equation P
y
and P
z
are the
second and the third highest probability values of the
age classes. We found that overlapping age groups
performs better with our implementation method than
the non-overlapping age groups.
3 GEOMETRIC FEATURES
Aging causes significant variations in the anatomy
of human face especially during the transition period
from childhood to adulthood. Changes in the shape
of the face across ages can play a critical role in age
estimation. In order to describe the human face ge-
ometrically, ratios of distance values between facial
landmark points according to face anthropometry can
be used (Kwon and Lobo, 1999). Face anthropome-
try is the science of measuring size and proportions
on human faces (Ramanathan and Chellappa, 2006).
Anthropometric data have been widely used in gen-
erating geometric models of human face (DeCarlo
et al., 1998), in characterizing growth related shape
variations (Ramanathan and Chellappa, 2006) for the
face recognition applications and in constructing face
models for computer graphics.
In our age estimation as illustrated in Figure 3(a)
we obtain 38 facial landmarks from 68 points which
are read from point files that are provided for ev-
ery face images in Face and Gesture Recognition
Research Network (FG-NET) (FGNET, 2010)Aging
Database. In order to further test the method on the
MORPH database (Ricanek Jr. and Tesafaye, 2006),
same facial landmarks are extracted automatically for
each face image in the database. Then, to model the
geometric shapes of human faces at different ages, we
extract 34 facial proportions, ratios of distances be-
tween above mentioned facial landmarks as shown in
Figure 3(b). Some of the facial proportions which
are used as geometric features of the classifier are;
r
1
: (
p8−p16
p33−p17
), r
2
: (
p8−p38
p11−p5
), . . . , r
34
: (
p36−p34
p8−p27
) .
HUMAN AGE ESTIMATION VIA GEOMETRIC AND TEXTURAL FEATURES
533

(a)
(b)
Figure 3: (a) 38 facial landmarks which are read from point
files that are provided for face images in FG-NET aging
database, (b) Geometric features extraction process.
Although the geometric features of a face image are
insensitive to the changes in illumination, they might
be affected by head pose variations and camera dis-
tortions. In order to addres this problem, the two of
the geometric features that we use in age classifica-
tion are based on cross ratio of the face image. If p
1
,
p
2
, p
3
and p
4
are four distinct points on the same line,
then the cross ratio is computed as:
(p
1
, p
2
; p
3
, p
4
) =
(p
1
− p
3
)(p
2
− p
4
)
(p
2
− p
3
)(p
1
− p
4
)
(2)
The cross ratio is invariant to the projective trans-
formations. As illustrated in Figure 4, l
1
, l
2
, l
3
and l
4
are four coplanar lines passing through the
same point O. The cross ratio of these lines is de-
fined as the cross ratio of the intersections of these
lines with any other line that does not pass through
O. Therefore, the cross ratios (p
17
, p
19
; p
29
, p
33
) and
(p
17
0
, p
19
0
; p
29
0
, p
33
0
) are equal.
In our work, we model these lines as the lines
passing through the central projection of the camera
and the facial points. For the first cross ratio, we
use the eye corner points; (p17, p19; p29, p33) (Fig-
ure 4). For the second cross ratio, we use the head
point, center point of eye brows, mouth mid point and
chin point; (p16, p28; p38, p8). These two geometric
Figure 4: Cross ratio for the eye corner points.
features make our classification system robust against
the perspective distortions, because the cross ratio be-
tween four colinear points stays constant under per-
spective transformations.
4 TEXTURAL FEATURES
Facial aging effects, especially in older age groups,
are mostly perceived in the form of textural varia-
tions such as wrinkles, creases, and changes in skin
tone. Textural changes in human face provide fun-
damental information for the estimation of human
age. Thus, the effectiveness of the textural face repre-
sentation method is highly important for age estima-
tion. In face recognition applications, the LBP opera-
tor and Gabor filters are the most popular techniques
for face representation (Ahonen et al., 2004)(Ekenel
et al., 2008)(Marcel et al., 2007)(Bhuiyan and Liu,
2007)(Shan et al., 2004). We use LBP, Gabor and
LGBP features as textural features in age estimation
as explained below.
4.1 LBP Features
Local Binary Pattern is a non-parametric kernel which
summarizes the local spatial structure of an image
(Marcel et al., 2007). The original LBP operator la-
bels the pixel of the image by comparing it with the
surrounding pixels in its 3×3-neighbourhood as illus-
trated in Figure 5.
Figure 5: The original LBP operator.
The decimal form of the resulting 8-bit word (LBP
code) can be expressed as follows (Marcel et al.,
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
534

2007):
LBP(x
c
,y
c
) =
7
∑
n=0
s(i
n
− i
c
)2
n
(3)
where i
c
corresponds to the gray value of the center
pixel (x
c
,y
c
), i
n
to the gray value of the 8 surrounding
pixels, and function s(x) is defined as:
s(x) =
1 if x ≥ 0
0 if x < 0
(4)
Local binary pattern based face recognition has
been proposed as a robust face recognition algorithm
(Ahonen et al., 2004)(Ekenel et al., 2008). Therefore,
we use the LBP values of the pixels rather than the
raw intensities as the feature vector for the classifier.
4.2 Gabor Features
Gabor filters are one of the most effective texture rep-
resentation techniques for analyzing an image into a
detailed local description. Gabor features are com-
monly used in face representation for the face recog-
nition applications due to their robustness to image
variations (Bhuiyan and Liu, 2007)(Shan et al., 2004).
The Gabor representation of a face image is gener-
ated by convolving it with the Gabor filters (Bhuiyan
and Liu, 2007). Applying a Gabor filter Ψ
f ,Θ
(x,y) to
the pixel at the (x, y) pixel position in the image can
be defined as:
g
f ,Θ
(x,y) = f (x,y)∗Ψ
f ,Θ
(x,y) (5)
where f (x, y) corresponds to the intensity value
of the pixel, f and Θ are used for controlling the scale
and the oriantation of the Gabor filters respectively,
and
*
is referred as the convolution operator.
Figure 6: Convolution of the face image with the Gabor
filters.
When convolving a face image with a range of
Gabor filters at different orientations and scales, we
can get a set of filter responses that characterize the
local texture of the face image. In our method, we
use 12 Gabor filters with the following parameters:
f ∈ {1,1.5,2} and Θ ∈ {
π
8
,
2π
8
,
4π
8
,
6π
8
}. After con-
volving the face image with the Gabor filters, we ob-
tain 12 Gabor magnitude images with 3 distinct scales
and 4 distinct orientations as shown in Figure 6.
Table 1: The age range distribution of the images in the FG-
NET database.
Age Classes Number of Samples
(0-3) 141
(3-5) 120
(4-7) 156
(6-11) 201
(8-17) 321
(12-25) 361
(18-29) 210
(26-35) 100
(30-40) 88
(36-45) 55
(41-55) 49
(46-60) 27
(56-75) 9
Table 2: MAE of age estimation on FG-NET database.
Age Estimation Method MAE
Classifier1 (Geometric-no cross ratio) 7.86
Classifier2 (Geometric) 6.68
Classifier3 (Gabor) 10.24
Classifier4 (Geometric+Gabor) 9.35
Classifier5 (LBP) 8.94
Classifier6 (Geometric+LBP) 8.18
Classifier7 (LGBP) 9.55
Classifier8 (Geometric+LGBP) 5.05
4.3 LGBP Features
Local Gabor Binary Pattern which is the combination
of Gabor filters and the LBP operator, is used to en-
hance the information in the Gabor magnitude image.
LGBP representation combines the local intensity dis-
tribution with the spatial information (Zhang et al.,
2005). In order to generate the LGBP representation
of a face image; the face image is convolved with
multi-scale and multi-orientation Gabor filters first.
Then, the LBP operator is applied to each pixel of the
Gabor magnitude images as illustrated in Figure 7.
In order to obtain the LGBP representation of face
images, the LBP operator is applied to each pixel of
each 12 Gabor magnitude images. Then, we use the
pixel values of 12 LGBP representations as LGBP
features of the face image.
5 EXPERIMENTAL RESULTS
We performed age classification experiments on
the FG-NET Aging Database (FGNET, 2010) and
HUMAN AGE ESTIMATION VIA GEOMETRIC AND TEXTURAL FEATURES
535
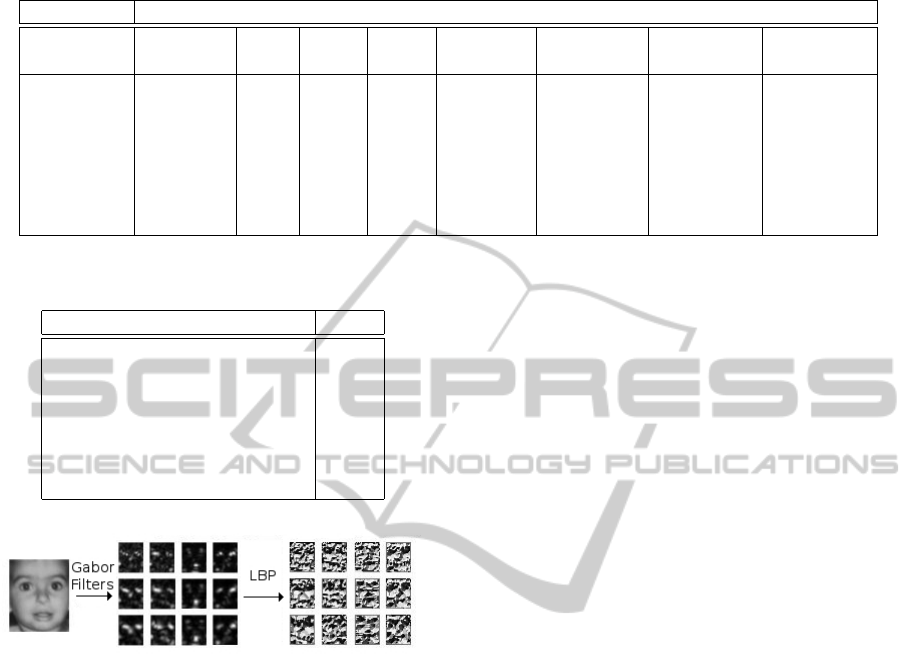
Table 3: MAE/D of age estimation on FG-NET database.
Age Ranges Feature Set
Geometric LBP Gabor LGBP Geo+LBP Geo+Gabor Geo+LGBP Geo+LGBP
(no overlap)
(0-10) 4.35 6.8 8.62 8.24 5.46 6.17 3.34 5.16
(11-20) 4.72 5.32 7.53 7.4 6.13 7.95 3.28 6.1
(21-30) 8.87 9.71 9.31 6.13 11.87 13.37 7.17 7.67
(31-40) 13.18 18.48 20.21 19.45 12.71 13.46 10.25 16.75
(41-50) 16.08 25.38 22.76 22.51 18.91 20.97 13.4 16.3
(51-60) 24.83 38.7 30.45 27.82 28.58 26.13 14.57 30.99
(61-70) 31.85 37.6 36.9 45.23 38.52 34.9 24.81 34.1
Table 4: MAE of age estimation on MORPH database.
Age Estimation Method MAE
Classifier2 (Geometric) 15.15
Classifier3 (Gabor) 9.73
Classifier4 (Geometric+Gabor) 8.11
Classifier5 (LBP) 12.33
Classifier6 (Geometric+LBP) 10.93
Classifier7 (LGBP) 8.58
Classifier8 (Geometric+LGBP) 6.28
Figure 7: LGBP face representation process.
MORPH Database (Ricanek Jr. and Tesafaye, 2006)
which are the most popular databases among the face
age estimation research community. The FG-NET
Aging database contains 1002 high-resolution color
or grayscale face images from 82 subjects ranging
from age 0 to 69. Images in the database display
facial appearance changes in pose, illumination, ex-
pression, etc. Also there are only few images of per-
sons older than 40 in the database. Table 1 shows
the age range distribution of the images that areused
in the FG-NET experiment. The MORPH Database
contains more than 55000 images of more than 13000
individuals ranging from age 16 to 77. The average
number of images per individuals is 4. For MORPH
experiment, we use 20 randomly selected samples for
each age value which range from age 16 to 65.
In FG-NET experiment, for each sample in
dataset, the age class values are labeled according
to the exact age information. We used the age class
scheme which is illustrated in Figure 1. Then for each
classifier, Leave-One-Person-Out (LOPO) evaluation
scheme is used. In each fold, all samples of a sin-
gle person are used as the testing set and the remain-
ing samples are used as the training set. For com-
parison purposes, we used the Mean Absolute Error
(MAE) (Lanitis et al., 2004) which is the most com-
monly used metric for age estimation. Table 2 shows
the MAE of age estimation for different kinds of fea-
tures which are used as face image feature vectors for
the age classifiers.
It can be observed in Table 2 that, using all textural
features in combination with the geometric features,
contributes positively to the performance of age es-
timation. The combination of LGBP and Geometric
features achieves 5.05 MAE on the FG-NET Aging
Database. Note also that, cross ratio is a very impor-
tant feature, because it improves the overall geometric
estimation results.
As previously mentioned, the images in the FG-
NET Database, are not equally distributed over age
ranges. For a detailed analysis of the age estima-
tion method, we calculated the MAE for each decade
seperately. The comparative results of the MAEs per
decade (MAE/D) for different kinds of features are
shown in Table 3.
As we previously mentioned, overlapping age
groups performs better with our interpolation method
than the non-overlapping age groups. In order to
verify this, we also tested our method with non-
overlapping age class scheme. The age is partitioned
into seven different classes such that ClassA (0-3),
ClassB (4-7), ClassC (8-17), ClassD (18-29), ClassE
(30-40), ClassF (41-55), ClassG (56-70), ClassH
(70+). The samples are assigned one group label. Our
best MAE for non-overlapping age groups was ob-
tained using the fusion of LGBP and Geometric fea-
tures as expected. The experimental results are shown
in the last column of Table 3. The comparative results
reveals that overlapping age groups performs remark-
ably better than the non-overlapping age groups.
The age class scheme which is used in FG-NET
experiment is not adequate for MORPH experiment,
because the face image dataset that used in MORPH
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
536

Table 5: MAE/D of age estimation on MORPH database.
Age Ranges Feature Set
Geometric LBP Gabor LGBP Geo+LBP Geo+Gabor Geo+LGBP
(10-20) 21.37 16.66 13.96 9.29 13.8 11.62 9.13
(21-30) 14.65 13.76 9.19 8.33 11.69 8.04 6.5
(31-40) 11.42 8.2 9.27 7.36 8.02 7.57 5.34
(41-50) 12.49 12.03 10.7 7.97 11.11 8.38 7.06
(51-60) 16.26 12.31 7.15 9.62 10.77 6.44 5.23
(61-70) 20.5 14.13 10.78 10.03 12.32 8.57 5.43
Figure 8: The overlapping age groups for MORPH
database.
experiment does not contain samples for age values
which range from 0 to 15. Therefore in MORPH ex-
periment, for age class labeling process, we used an-
other age class scheme which is illustrated in Figure
8. Then for each classifier, Leave-One-Out evaluation
scheme is used. In each fold, one sample is used as the
testing set and the remaining samples are used as the
training set. Table 4 shows the MAE of age estimation
on MORPH Database. As can be observed from Table
4, the combination of LGBP and Geometric features
achieves 6.28 MAE on MORPH Database.
For a detailed analysis of the age estimation
method, we calculated the MAE for each decade
seperately for MORPH Database. The comparative
results of the MAEs per decade (MAE/D) for differ-
ent kinds of features are shown in Table 5.
Table 6: MAE of different methods on FG-NET database.
Method MAE
(Geng et al., 2007) 6.77
(Geng et al., 2007) 8.06
(Guo et al., 2008) 5.07
(Yan et al., 2008) 4.95
(Guo et al., 2009) 4.77
Our Method 5.05
We can say that, the effectiveness of the fusion
of LGBP and Geometric features result from many
aspects. These include the LBP descriptor that cap-
tures small texture details, multi-scale and multi-
orientation Gabor features that encode facial texture
over a range of coarser scales. Finally, geometric pro-
portions that are used for the characterization of the
variations in facial shape contribute positively to the
age estimation.
Facial aging causes the most noticable variations
in one’s appearance during the formative years. As a
result, the estimated age of a young person is more
accurate than the older persons. As can be observed
from Table 3, the MAE of age estimation at young
ages is lower than the MAE of age estimation at
old ages. Besides, in FG-NET experiment, there are
only few old person images are used which are not
enough for creating a general age estimation model.
In MORPH experiment, we used same number of im-
ages for each age value and we get similar MAE val-
ues for each decade.
We also compared our results with the state of the
art methods that follow the same popular Leave-One-
Person-Out (LOPO) test strategy. As shown in Table
6, our method performs comparably with the state of
the art approaches on age estimation.
6 CONCLUSIONS
We presented an age estimation method that combines
the geometric and textural features of human face. We
propose to use overlapping age groups and a classifier
to assign probabilities of a face image belonging to
each group. The interpolation of the classifier proba-
bilities produces the final estimated age. This method
has the advantage of using robust classifiers in the
process of numerical age estimation.
Our age group classifiers employ textural fea-
tures, geometric features, and fusion of these features.
Comparative experiments for different features show
that for each textural feature, the fusion with the geo-
metric features provides significant improvements. In
this paper, we used the fusion of geometric features
and one textual feature set (LBP, Gabor, LGBP). The
fusion of more than two feature sets might achieve
better results. Employment of the cross ratio tech-
nique in geometric features improved the classifica-
tion rates considerably. When we use the combination
of LGBP and Geometric features in the AdaBoost al-
gorithm, we obtain 5.05 and 6.28 MAE of age esti-
mation for FG-NET and MORPH Databases respec-
HUMAN AGE ESTIMATION VIA GEOMETRIC AND TEXTURAL FEATURES
537

tively. We formed different age class schemes for
different datasets by using a heuristic approach. Our
future work will concentrate on generating age class
scheme automatically according to the characteristics
of the dataset that used in the age estimation experi-
ments.
ACKNOWLEDGEMENTS
The authors would like to thank Dr. K. Ricanek
of UNCW for providing the MORPH Face Aging
Database (Ricanek Jr. and Tesafaye, 2006) and they
would also like to thank the FG-NET consortium
for providing the FG-NET Aging Database (FGNET,
2010).
REFERENCES
Ahonen, T., Hadid, A., and Pietikainen, M. (2004). Face
Recognition with Local Binary Patterns. In Computer
Vision - ECCV 2004, pages 469–481.
Bhuiyan, A. and Liu, C. H. (2007). On face recognition
using gabor filters.
Burt, D. M. and Perrett, D. I. (1995). Perception of age in
adult caucasian male faces: Computer graphic manip-
ulation of shape and colour information. Proceedings
of the Royal Society of London. Series B: Biological
Sciences, 259(1355):137–143.
DeCarlo, D., Metaxas, D., and Stone, M. (1998). An an-
thropometric face model using variational techniques.
In Proceedings of the 25th annual conference on
Computer graphics and interactive techniques, SIG-
GRAPH ’98, pages 67–74, New York, NY, USA.
ACM.
Ekenel, H., Fischer, M., Tekeli, E., Stiefelhagen, R., and
Ercil, A. (2008). Local binary pattern domain local
appearance face recognition. In Signal Processing,
Communication and Applications Conference, 2008.
SIU 2008. IEEE 16th, pages 1–4.
FGNET (2010). The FG-NET Aging Database [On-
line]. Available: http://www.fgnet.rsunit.com/, 2010.
http://www.fgnet.rsunit.com.
Freund, Y. and Schapire, R. E. (1996). Experiments with
a New Boosting Algorithm. In In Proceedings of
the Thirteenth International Conference on Machine
Learning, pages 148–156.
Fu, Y., Guo, G., and Huang, T. (2010). Age synthesis and
estimation via faces: A survey. IEEE Transactions on
Pattern Analysis and Machine Intelligence, 32.
Gao, F. and Ai, H. (2009). Face age classification on
consumer images with gabor feature and fuzzy lda
method. In Proceedings of the Third International
Conference on Advances in Biometrics, ICB ’09,
pages 132–141, Berlin, Heidelberg. Springer-Verlag.
Geng, X., hua Zhou, Z., and Smith-Miles, K. (2007). Au-
tomatic age estimation based on facial aging patterns.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 29:2234–2240.
Guo, G., Fu, Y., Dyer, C., and Huang, T. (2008). Image-
based human age estimation by manifold learning and
locally adjusted robust regression. Image Processing,
IEEE Transactions on, 17(7):1178–1188.
Guo, G., Mu, G., Fu, Y., and Huang, T. (2009). Human age
estimation using bio-inspired features. In Computer
Vision and Pattern Recognition, 2009. CVPR 2009.
IEEE Conference on, pages 112–119.
Kwon, Y. H. and Lobo, N. D. V. (1999). Age classification
from facial images. In In Proc. IEEE Conf. Computer
Vision and Pattern Recognition, pages 762–767.
Lanitis, A., Draganova, C., and Christodoulou, C. (2004).
Comparing different classifiers for automatic age es-
timation. IEEE Trans Syst Man Cybern B Cybern,
34(1):621–8.
Marcel, S., Rodriguez, Y., and Heusch, G. (2007). On the
recent use of local binary patterns for face authen-
tication. International Journal on Image and Video
Processing Special Issue on Facial Image Processing.
IDIAP-RR 06-34, accepted for publication but with-
drawn because of author charges.
Ramanathan, N. and Chellappa, R. (2006). Modeling age
progression in young faces. In Computer Vision and
Pattern Recognition, 2006 IEEE Computer Society
Conference on, volume 1, pages 387–394.
Ramanathan, N. and Chellappa, R. (2008). Modeling shape
and textural variations in aging faces. In Automatic
Face Gesture Recognition, 2008. FG ’08. 8th IEEE
International Conference on, pages 1–8.
Ricanek Jr., K. and Tesafaye, T. (2006). Morph: A longitu-
dinal image database of normal adult age-progression.
In Proceedings of the 7th International Conference on
Automatic Face and Gesture Recognition, FGR ’06,
pages 341–345, Washington, DC, USA. IEEE Com-
puter Society.
Shan, S., Gao, W., Chang, Y., Cao, B., and Yang, P.
(2004). Review the Strength of Gabor Features for
Face Recognition from the Angle of Its Robustness
to Mis-Alignment. Pattern Recognition, International
Conference on, 1:338–341.
Yan, S., Zhou, X., Liu, M., Hasegawa-Johnson, M., and
Huang, T. (2008). Regression from patch-kernel.
In Computer Vision and Pattern Recognition, 2008.
CVPR 2008. IEEE Conference on, pages 1–8.
Yang, Z. G. and Ai, H. Z. (2007). Demographic Classifica-
tion with Local Binary Patterns. Biometric Authenti-
cation, pages 464–473.
Zhang, W., Shan, S., Gao, W., Chen, X., and Zhang, H.
(2005). Local gabor binary pattern histogram se-
quence (lgbphs): a novel non-statistical model for face
representation and recognition. In Computer Vision,
2005. ICCV 2005. Tenth IEEE International Confer-
ence on, volume 1, pages 786–791 Vol. 1.
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
538
