RENDERING VIRTUAL OBJECTS INTO REAL SCENE

BY USING A DIFFUSE SPHERE

Yuji Kanda

, Fumihiko Sakaue

, Jun Sato

, Kazuhisa Ishimaru

and Masayuki Imanashi

Nagoya Institute of Technology, 466-8555 Nagoya, Japan

NIPPON SOKEN Inc., 445-0012 Nishio, Japan

DENSO Corporation, 448-8661 Kariya, Japan

Keywords:

Augmented Reality, Diffuse Sphere, Light Source Distribution, Shading, Shadows.

Abstract:

In this paper, we propose an efﬁcient method for rendering virtual objects into real scene images. We put a

diffuse sphere into the scene as a reference object, and use the direct relationship between the intensity of the

diffuse sphere and the intensity of virtual objects for rendering the virtual objects in images. We also generate

shadows of the virtual objects by using shadows of the reference sphere. As a result, arbitrary virtual objects

and their shadows can be rendered quite efﬁciently from a single diffuse sphere put in the scene. The proposed

method is tested in real image experiments, and evaluated quantitatively comparing with the existing method.

1 INTRODUCTION

Rendering virtual objects into real scenes is very use-

ful for making movies and for designing augmented

reality systems. For generating realistic augmented

reality images, it is very important to generate accu-

rate shade and shadow of virtual objects in images.

The existing methods generate shade and shadow

of objects by estimating light source distributions of

the scene (Marschner and Greenberg, 1997). The

spherical mirror is often used for measuring light

source distributions (Debevec, 1998; Kanbara and

Yokoya, 2004). In these methods, a camera observes

the spherical mirror put in the scene, and the light

source distributions are measured from the camera

image directly. Although these methods are simple

and efﬁcient, cameras in general do not have enough

dynamic range to measure the light source distribu-

tions directly. Thus, these methods require to take

multiple images changing the shutter speed of the

camera. For solving the problem, known diffuse ob-

jects such as diffuse spheres were also used for esti-

mating the light sources (Zhang and Yang, 2001; Wei,

2003; Takai et al., 2004; Weber and Cipolla, 2001).

These methods use the boundary lines on diffuse ob-

jects, which separate illuminated and un-illuminated

areas for estimating light source orientations. How-

ever, extracting these boundary lines on diffuse ob-

jects is not easy in practice. Furthermore, it is difﬁc-

Figure 1: The reference sphere and a plane put in the scene.

We use a diffuse sphere and a plane for generating shading

information and shadows of virtual objects.

ult for these methods to estimate light source distribu-

tions which consist of many light sources. As shown

in these research, accurate estimation of light source

distributions is not easy in practice.

Thus, we in this paper propose an efﬁcient

method for rendering virtual objects into real scenes

without estimating light source distributions as far as

possible. In our method, we use a diffuse sphere put

in the scene as a reference object as shown in Fig. 1.

Our method separates the task of shading and the task

of shadowing. We separate these two tasks, since we

generate shading information without estimating light

source distributions of the scene, while we generate

shadows by estimating the light source distributions.

For generating shading information of virtual ob-

279

Kanda Y., Sakaue F., Sato J., Ishimaru K. and Imanishi M..

RENDERING VIRTUAL OBJECTS INTO REAL SCENE BY USING A DIFFUSE SPHERE.

DOI: 10.5220/0003850202790285

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 279-285

ISBN: 978-989-8565-03-7

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

jects, we use the direct relationship on intensity be-

tween the virtual object and the diffuse sphere. The

proposed method is very efﬁcient and reasonably ac-

curate, since this method does not need to estimate

light source distributions, and does not suffer from the

estimation error of light source distributions.

For generating the shadow of virtual objects, we

use the shadow of reference diffuse sphere. If we

have a known object on a ground plane, the shadow

of the object on the plane is a very useful cue to esti-

mate light source distributions. Sato et al. (Sato et al.,

2003) proposed a method for estimating light source

distributions from shadows on a plane, which are gen-

erated by known objects. However, their method as-

sumes that there is no inter reﬂection between the ob-

ject and the plane. Hence, their method suffers from

the inter reﬂections, if the reﬂectance of the object is

large. Thus, we in this paper estimate light source

distributions from shadows of a diffuse sphere taking

account of the effect of inter reﬂections between the

sphere and the plane. As a result, virtual objects and

their shadows can be rendered quite efﬁciently and ac-

curately from a single diffuse sphere put in the scene.

In the following sections, we ﬁrst propose an ef-

ﬁcient method for generating shading information of

virtual objects from a reference diffuse sphere with-

out using light source information. We next propose

a method for generating shadows by estimating light

source distributions from the shadow of the reference

sphere. We in this paper assume all the light sources

are at inﬁnity, and virtual objects put into the scene do

not emit any light and are Lambertian.

2 SYNTHESIZING VIRTUAL

OBJECTS INTO THE SCENE

The standard method for synthesizing virtual objects

into real scene is based on the estimation of light

sources of the scene. Suppose we have M light

sources at inﬁnity, whose directions are represented

by unit vectors s

(k = 1, ··· , M), and magnitudes are

= [E

, E

]

⊤

(k = 1, ··· , M) in red, green and

blue color channels. If the object surface is Lamber-

tian, the image intensity I

= [I

, I

]

⊤

of ith point

on the surface illuminated by E

(k = 1, ··· , M) can

be described as follows:

∑

k=1

⊤

(1)

where n

denotes the surface normal at the ith point,

and v

denotes a visibility function, which takes 1 if

the ith point is illuminated from the kth light source,

and takes 0 in the other case. R

is a 3 × 3 diag-

onal matrix whose diagonal components are the re-

ﬂectance of the surface point ρ

, ρ

in R, G and

B components as follows:





0 0

0 ρ

0 0 ρ





(2)

C denotes the characteristic function of the camera,

which represents the response of the camera in R, G

and B channels, i.e. the gain of output signals with re-

spect to input signals. In general the crosstalk among

R, G and B channels is very small and negligible, and

thus we assume the matrix C is also diagonal as fol-

lows:

C =





0 0

0 C

0 0 C





(3)

where, C

, C

and C

denote gains in each channel.

We in this paper assume that the gamma correction

does not exist in the camera, and its characteristic

function is linear.

From (1), we ﬁnd that we need light source in-

formation E

in each orientation s

and camera char-

acteristics C for synthesizing the image intensity of

virtual objects. Thus, the existing methods estimate

light source information of the scene by using various

cues, such as shadows and shading, and measure the

characteristic function of the camera by using color

chart etc. However, the results suffer from the mea-

surement errors of these components.

Thus, we in this paper propose a method which

enables us to compute the image intensity of virtual

objects without estimating light sources and camera

characteristic functions. In our method, we put a dif-

fuse sphere in the scene as a reference object as shown

in Fig. 1, and use its image information for synthesiz-

ing virtual objects into the scene. Since the sphere has

surface normals in all the directions, the surface nor-

mal of any point on a virtual object in the scene has

its reference surface normal on the sphere. Although

not all the surface normals are visible in a single cam-

era image, all the visible surface normals of virtual

objects have their references in the visible part of the

sphere, if we assume afﬁne projection.

Now, let us consider an image intensity I

′

of a jth

point on the reference sphere, whose surface normal

′

is identical with the surface normal n

of ith point

on the virtual object, i.e. n

′

= n

. Then, I

′

can be

described as follows:

′

∑

k=1

′

⊤

(4)

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

280

where, R

′

is the reﬂectance matrix of the jth point on

the reference sphere, and v

′

is a visibility function of

the point with respect to the kth light source. If the

object is convex, v

is identical with v

′

. If the object

is not convex, v

is not completely identical with v

′

However, in most of the case, v

is close to v

′

. Thus,

we in this paper assume v

and v

′

are identical.

Since both C and R are diagonal, (1) and (4) can

be described as follows:

= R

L (5)

′

= R

′

L (6)

where,

L =

∑

k=1

⊤

(7)

From (5) and (6), we ﬁnd that the image intensity I

of the virtual object can be computed from the image

intensity I

′

of the reference sphere as follows:

= R

′

−1

′

(8)

As a result, we do not need to estimate light source

distributions nor characteristic function of cameras

for synthesizing virtual objects into the real scene im-

ages. Thus, the proposed method is very simple and

efﬁcient.

Since the image of the reference sphere is digital

and the surface normals of the reference sphere are

discrete in practice, we compute the image intensity

′

of a point on the reference sphere, whose surface

normal is identical with that of the virtual object, by

using the linear interpolation. To ensure a reasonable

accuracy of synthetic image generation, the reference

sphere in the image should not be too small.

3 SYNTHESIZING SHADOW OF

VIRTUAL OBJECTS

We next consider a method for generating shadow of

objects. For realistic virtual images, it is very impor-

tant to generate realistic shadows on the ﬂoor. We

generate shadow of virtual objects by using the same

reference sphere used for shading virtual objects.

Suppose the reference sphere is put on a planar

Lambertian surface. Then, the shadows of the sphere

appears on the planar surface, and they are visible

from the scene camera. These image shadows pro-

vide us useful information for generating the shadows

of virtual objects put in the scene. Sato et al. (Sato

et al., 2003) proposed an efﬁcient method for estimat-

ing light source distributions from shadows of scene

Figure 2: Sampling of light source distributions on a

geodesic dome. Each patch on the dome represents the di-

rection of each light source.

objects. We extend their method for estimating light

source distributions and generating shadows from the

reference sphere. Sato et al. assumed that there is

no inter reﬂection between the scene objects and the

planar surface, and estimated the light source distri-

bution from the shadows of the scene objects on the

planar surface. This assumption is reasonable if the

reﬂectance of objects is small, and the form factors

between the object and the plane are also small. The

form factor is the visibility between two patches on

surfaces, and it becomes large if the relative orienta-

tion between normals of these two patches is close to

π radian and these patches are close to each other. In

our method, we use a reference sphere put on a plane.

The reference sphere and the plane are very close to

each other at around the contact point of these two ob-

jects. Furthermore, the relative orientation of two sur-

faces is close to π radian at around the contact point.

Thus, inter reﬂections are not negligible in the esti-

mation of light source distributions. Therefore, we

propose a method for estimating light source distribu-

tions and generating shadows taking account of inter

reﬂections.

3.1 Sampling of Light Source

Distribution

In order to estimate light source distributions under

multiple lights, we represent the light source distribu-

tions by using a geodesic dome as shown in Fig.2. In

this model, a light source distribution is represented

by the magnitude of light source E

= [E

, E

]

⊤

(k = 1, ··· , M) in M light source directions s

(k =

1, ··· , M), which are represented by M patches on

the geodesic dome. Since s

(k = 1, · ·· , M) is prede-

ﬁned on the geodesic dome, the estimation of a light

source distribution is same as the estimation of E

(k = 1, ··· , M).

RENDERING VIRTUAL OBJECTS INTO REAL SCENE BY USING A DIFFUSE SPHERE

281

3.2 Light Source Distributions from

Shadows of Reference Objects

Let us consider a reference object, which consists of a

sphere and a plane with known reﬂectance, as shown

in Fig. 1. Although many other objects exist in the 3D

space, we consider these other objects as light sources

at inﬁnity, and these light sources illuminate the ref-

erence object. Hence, the inter reﬂection occurs be-

tween the reference sphere and the reference plane,

but it does not occur between the reference object and

other objects in the 3D space. This assumption is

valid in most of the case, since the distance between

the reference object and other objects are much larger

than the distance between the reference sphere and

the reference plane in general. Thus, we model the

3D world by the reference object and light sources at

inﬁnity, which are represented by a geodesic dome.

Suppose we have N patches on the reference ob-

ject, and M patches on the geodesic dome. Then, M

patches on the geodesic dome emit light, and the inter

reﬂection occurs among N patches on the reference

object. Then, the following radiosity equation holds:

∑

j=1

∑

k=1

(9)

where, the ﬁrst term in the right side of (9) represents

the inter reﬂection and the second term represents the

direct illumination by light sources on the geodesic

dome.

denotes the form factor between ith and jth

patches on the reference object, and G

denotes the

form factor between ith patch on the reference object

and kth patch on the geodesic dome. These are de-

scribed as follows:

cosθ

πr

(10)

cosθ

(11)

where, A

denotes the area of ith patch, and θ

denotes

the angle between the surface normal of ith patch and

a ray between two patches. r is the distance between

two patches. Note, r

term does not exist in G

, since

each patch on the geodesic dome represents a light

source at inﬁnity, and its energy does not decrease

with respect to the distance r. Also, each patch on the

geodesic dome is front-parallel, and thus cosθ

= 1.

This is why cosθ

does not exist in (11).

Since we have N patches on the reference object

and M patches on the geodesic dome, we can derive

the following system of linear equations from (9).







··· G













′













−

∑

−

∑

N j







(12)

where, E

′

is a light source distribution multiplied by

the camera characteristic function C as follows:

′

= CE

(k = 1, ··· , M) (13)

We in this paper estimate E

′

instead of E

, which en-

ables us to generate virtual shadows without knowing

camera parameters C. If N ≥ M, we can estimate the

light source distribution E

′

(k = 1, · ·· , M) by solving

(12) taking account of the inter reﬂection between the

reference sphere and the reference plane.

3.3 Synthesizing Shadows

Once the light source distribution is estimated, the

shadow of virtual objects can be generated from the

distribution.

Let us consider an image point P in the ith patch

on the ground plane, whose image intensity is I

and

reﬂectance is R

. Let G

be the form factor between

the ith patch on the ground plane and kth patch on the

geodesic dome before putting virtual objects, and let

′

be that after putting the virtual objects. Both G

and G

′

can be computed easily from the geometric

relationship between the virtual objects and the light

source directions. Then, if we neglect inter reﬂec-

tions, the image intensities of point P before and after

putting the virtual objects are described as follows:

∑

k=1

′

(14)

= Dr

(15)

′

∑

k=1

′

(16)

= D

′

(17)

where, D and D

′

are diagonal matrices, whose diag-

onal components are

∑

k=1

′

and

∑

k=1

′

re-

spectively, and r

is a three vector which consists of

the three diagonal components of R

Then from (15) and (17), we ﬁnd that the image

intensity I

′

of point P after putting the virtual objects

can be computed from the image intensity I

of the

point before putting the virtual objects as follows:

′

= D

′

−1

(18)

As shown in (18), the image intensity of shadows can

be computed without knowing reﬂectance R

of the

ground plane and camera parameters C.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

282

Figure 3: The image of the reference sphere and synthesized

virtual objects (person, pod).

Figure 4: The light source distribution estimated from Fig. 3

by using the proposed method.

4 EXPERIMENTS

4.1 Real Image Experiments

We next show the results of some real image exper-

iments. In these experiments, we synthesize virtual

objects into real scene images. The virtual objects

are rendered by using the method shown in section 2,

and their shadows are rendered by using the method

shown in section 3.

Fig. 3 shows the image of a reference sphere and a

reference plane. The intensity of the sphere was used

for rendering virtual objects into the image, and the

shadow of the sphere was used for estimating the light

source distributions and rendering shadows of the vir-

tual objects into the image. Fig. 4 shows the light

source distribution estimated from Fig. 3 by using the

proposed method. The light source distribution was

measured at 225 points on the geodesic dome. Fig. 3

shows virtual objects (i.e. person, pod) and their shad-

ows rendered by using the proposed method. Fig. 5

and Fig. 6 show another example of image synthesis

under a different light source distribution. As shown

in these ﬁgures the shade and shadow of the virtual

Figure 5: The image of the reference sphere and synthesized

virtual objects (person, pod).

Figure 6: The light source distribution estimated from Fig. 5

by using the proposed method.

objects were generated properly, although the light

source distributions of the scene are very complex.

4.2 Accuracy Evaluation

We next evaluatethe accuracy of the proposed method

comparing with other methods. In this evaluation, we

use synthetic images for quantitative evaluation.

Fig. 7 shows the synthetic 3D scene of the ref-

erence object used in our experiments. The refer-

ence sphere and the plane are Lambertian and their

reﬂectance is 0.6 in R, G and B. The light source dis-

tribution used for generating the scene is shown in

Fig. 8. There are 75 light sources on the geodesic

dome. Fig. 9 shows an image of the scene observed by

a virtual camera. The number of the observed patches

of the reference object was 83, and that of the ground

plane was 374. The Gaussian image noises with the

standard deviation of 1.0 were added to the image in-

tensity of each point, while the range of image inten-

sity is from 0 to 255. We estimated the light source

distribution of this scene from the image shown in

Fig. 9 by using the proposed method. We also esti-

mated the light source distribution by using the exist-

ing method proposed by Sato et al. (Sato et al., 2003)

for comparison.

RENDERING VIRTUAL OBJECTS INTO REAL SCENE BY USING A DIFFUSE SPHERE

283

-2

0.0

0.5

1.0

1.5

2.0

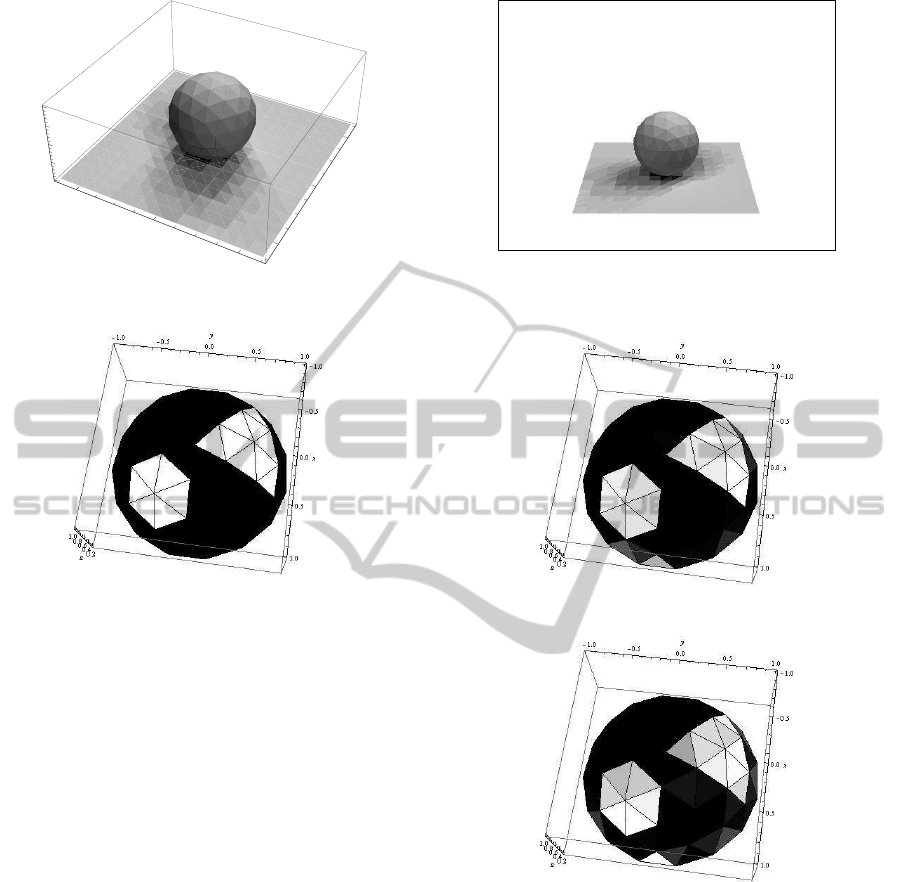
Figure 7: 3D scene used in our simulation experiments.

Figure 8: The light source distribution used in the simula-

tion experiments.

Fig. 10 (a) shows the light source distribution es-

timated by using the proposed method, and Fig. 10

(b) shows that of the existing method. From Fig. 10

and Fig. 8, we ﬁnd that the proposed method provides

us better estimation of light source distribution com-

paring with the existing method. The RMS error of

the estimated light source distribution divided by the

maximum ground truth light source magnitude was

0.14 in the proposed method and was 0.40 in the ex-

isting method.

We next evaluated the accuracy of estimated light

source distribution changing the reﬂectance of the

reference object. Fig. 11 shows the RMS error of

light source distributions estimated from the proposed

method and the existing method. The horizontal axis

shows the reﬂectance of the reference object, and the

vertical axis shows RMS error divided by the maxi-

mum light source magnitude. As shown in this ﬁgure,

if the reﬂectance of the reference object is small, the

error of estimation is small in both methods. How-

ever, if the reﬂectance of the reference object is large,

the accuracy of the existing method (Sato et al., 2003)

degrades drastically, while the proposed method still

provides us good accuracy. This is because the ex-

isting method suffers from inter reﬂections, when the

reﬂectance of the reference object is large.

Figure 9: The synthetic image generated by projecting the

3D scene shown in Fig. 7.

(a) Proposed method.

(b) Existing method.

Figure 10: The light source distribution estimated by using

the proposed method (a) and the existing method (b). The

ground truth is shown in Fig. 8.

5 CONCLUSIONS

In this paper, we proposed an efﬁcient method for

synthesizing virtual objects into real scene images

by using a diffuse reference sphere. The proposed

method uses the direct relationship between the inten-

sity of the reference sphere and the intensity of virtual

objects for generating the shading information of ob-

jects. Also, the proposed method generate shadows of

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

284

0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

reectanc

0.0

0.2

0.4

0.6

0.8

1.0

error

Figure 11: The accuracy of estimated light source distribu-

tions. If the reﬂectance of the reference object is large, the

accuracy of the existing method (Sato et al., 2003) degrades

drastically, while that of the proposed method does not.

the virtual objects by using the shadows of the refer-

ence sphere. As a result, the virtual objects and their

shadows can be rendered quite efﬁciently from a sin-

gle diffuse sphere put in the scene.

We tested the proposed method by using real

scene images. We also evaluated the accuracy of

the proposed method by using a synthetic 3D scene

comparing with the existing method. The proposed

method can synthesize virtual objects quite efﬁciently

with reasonable accuracy, and thus it is very useful.

The future work includes the extension of the pro-

posed method to the video streams, so that moving

virtual objects and their shadows are rendered prop-

erly into real scene videos.

REFERENCES

Debevec, P. (1998). Rendering synthetic objects into real

scenes: Bridging traditional and image-based graphics

with global illumination and high dynamic range pho-

tography. In Proc. SIGGRAPH 98, pages 189–198.

Kanbara, M. and Yokoya, N. (2004). Shadow representation

for augmented reality by estimating light environment

and shape of real scene. In Proc. MIRU, volume 2,

pages 247–252.

Marschner, S. and Greenberg, D. (1997). Inverse lighting

for photography. In Proc. Color Imaging Conference,

pages 262–265.

Sato, I., Sato, Y., and Ikeuchi, K. (2003). Illumination from

shadows. IEEE Transaction on Pattern Analysis and

Machine Intelligence, 25(3):290–300.

Takai, T., Nishimura, K., Maki, A., and Matsuyama, T.

(2004). Difference sphere: an approach to near light

source estimation. In Proc. IEEE Conference on Com-

puter Vision and Pattern Recognition, pages 98–105.

Weber, M. and Cipolla, R. (2001). A practical method for

estimation of point light sources. In Proc. British Ma-

chine Vision Conference, pages 471–480.

Wei, J. (2003). Robust recovery of multiple light source

based on local light source constant constraint. Pattern

Recognition Letters, 24(1–3):159–172.

Zhang, Y. and Yang, Y. (2001). Multiple illuminant di-

rection detection with application to image synthesis.

IEEE Transaction on Pattern Analysis and Machine

Intelligence, 23(8):915–920.

RENDERING VIRTUAL OBJECTS INTO REAL SCENE BY USING A DIFFUSE SPHERE

285