HUMAN RE-IDENTIFICATION THROUGH DISTANCE METRIC

LEARNING BASED ON JENSEN-SHANNON KERNEL

Yoshihisa Ijiri

, Shihong Lao

, Tony X. Han

and Hiroshi Murase

Corporate R&D, OMRON Corp., Kizugawa, Kyoto, Japan

OMRON Social Solutions Co. Ltd., Kizugawa, Kyoto, Japan

Electrical & Computer Engineering Dept., Univ. of Missouri, Columbia, MO, U.S.A.

Graduate School of Information Science, Nagoya Univ., Chigusaku, Nagoya, Japan

Keywords:

Human Re-identiﬁcation, Distance Metric Learning, Jensen-Shannon Kernel.

Abstract:

Human re-identiﬁcation, i. e., human identiﬁcation across cameras without an overlapping view, has important

applications in video surveillance. The problem is very challenging due to color and illumination variations

among cameras as well as the pose variations of people. Assuming that the color of human clothing does

not change quickly, previous work relied on color histogram matching of clothing. However, naive color

histogram matching across camera network is not robust enough for human re-identiﬁcation. Therefore, we

learned an optimal distance metric between color histograms using a training dataset. The Jensen-Shannon

kernel is proposed to learn nonlinear distance metrics. The effectiveness of the proposed method is validated

by experimental results.

1 INTRODUCTION

With the continuous drop of hardware costs, the num-

ber of surveillance cameras deployed havebeen grow-

ing drastically, leaving the available human analysts

far behind. To ﬁll this gap, many automatic video

surveillance techniques and systems have been pro-

posed. Among them, human identiﬁcation, which is

one major problem in video surveillance, enables us

to match human tracks in surveillance areas such as

stores and shopping malls for the purposes of secu-

rity or marketing. For law enforcement, with one or

more images of suspects, automatic human identiﬁ-

cation speeds up the process of ﬁnding them from a

large amount of surveillance camera records. Con-

sidering the cost effectiveness and the psychological

effects on the citizenry, it is impractical to fully cover

the entire surveillance area without any blind spot us-

ing the camera network. Therefore, in general, human

identiﬁcation needs to be done across cameras with

non-overlapping views. In this paper, this human re-

identiﬁcation problem is studied.

It is natural to tackle the human re-identiﬁcation

through the face recognition approach, which has

been studied extensively in the computer vision com-

munity. However, as shown in Fig. 1, people tend

to vary their poses a lot unless they are asked not

to do so. Surveillance cameras are also intended to

watch a large area. Hence it is unrealistic to assume

that clear human faces can always be viewed. There-

fore, for practical surveillance, face recognition alone

is insufﬁcient to guarantee the human identiﬁcation

accuracy. As a approach complementary to the face

recognition approach, human identiﬁcation based on

clothing colors is studied in this paper. Taking most

of the surveillance scenarios into consideration, we

assume that people do not change their clothing in a

short time duration, Noticing the symmetry character-

istic of human clothing, we conclude that the colors of

most clothing are view-angle insensitive.

Human re-identiﬁcation is a very challenging

problem for the following reasons. Among surveil-

lance cameras, color calibrations are not always the

(a) (b) (c) (d) (e) (f)

Figure 1: Sample images from VIPeR dataset: (a)(b) are

from ID 302, (c)(d) from ID 188, and (e)(f) from ID 358.

603

Ijiri Y., Lao S., X. Han T. and Murase H..

HUMAN RE-IDENTIFICATION THROUGH DISTANCE METRIC LEARNING BASED ON JENSEN-SHANNON KERNEL.

DOI: 10.5220/0003850506030612

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 603-612

ISBN: 978-989-8565-03-7

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

same. Also, the illuminations of different camera

views usually varies a lot. In addition, the pose

variations of people make it infeasible to expect

identical appearances among cameras. Many works

have addressed these difﬁculties and can be summa-

rized into the following three groups: (i) appearance-

based methods, (ii) color calibration or color transfer

function estimation between cameras, and (iii) inter-

camera relationship modeling.

For appearance-based methods, various features

have been proposed to represent clothing colors and

textures (Bird et al., 2005; Gheissari et al., 2006;

Wang et al., 2007; Gray and Tao, 2008; Lin and

Davis, 2008; Hamdoun et al., 2008; Schwartz and

Davis, 2009; Kuo et al., 2010; Bak et al., 2010; Alahi

et al., 2010; Berdugo et al., 2010; Bazzani et al.,

2010; Farenzena et al., 2010; Hirzer et al., 2011).

Among them, Farenzena et al. (Farenzena et al.,

2010) combined weighted HSV histograms, Maxi-

mally Stable Color Regions (MSER), and Recurrent

High-Structured Patches. The former two features are

used to represent clothing colors, and the last one

is for texture description. In the feature extraction

process, according to the symmetric and asymmetric

axes, the human body is divided into sub-regions to

deal with pose variations using an algorithm called the

Symmetric Driven Accumulation of Local Features

(SDALF). More recently, Bak et al. (Slawormir et al.,

2011) proposed to use mean Riemannian covariance,

which consists of covariance matrices of RGB colors,

corresponding gradient magnitudes, and orientations

from multiple shots.

These state-of-the-art appearance-based algo-

rithms achieve high accuracy through extraction of

multiple features. More speciﬁcally, color histograms

in various color spaces and local descriptors are com-

bined. These redundant feature extractions contribute

higher accuracy at the expense of computational efﬁ-

ciency. Among these features, clothing color-based

features are exploited extensively, because they are

robust to pose variation. For the color histogram

matching, traditional distances are used in various

color spaces. However, since the color calibrations

from different cameras are different, matching di-

rectly with traditional distances may lead to bias. So

the estimation of color relationships between cam-

eras, i.e. the algorithm group (ii) mentioned above,

has been studied in (Javed et al., 2008; Prosser et al.,

2008b; Prosser et al., 2008a; Gilbert and Bowden,

2006). Among these algorithms, the brightness trans-

fer function (BTF) method achieves quite good per-

formance. One disadvantage of BTF is that the BTF

between each pair of cameras has to be estimated. If

we have N cameras, then N(N −1)/2 BTFs must be

estimated. The computational complexity of the al-

gorithm w.r.t number of cameras is O (N

), which is

not practical for surveillance systems with many cam-

eras.

For camera networks, if people walk away from

one camera to another, and the entrance/exit times

of each camera can be modeled statistically. For in-

stance, a person exiting from a camera usually ap-

pears in another camera within a certain elapsed time.

Based on this concept, inter-camera relationship mod-

eling methods, categorized as algorithm group (iii),

have been proposed in (Javed et al., 2008; Huang and

Russell, 1997; Pasula et al., 1999; Song and Roy-

Chowdhury, 2007). The disadvantage of this scheme

is that such methods assume correct correspondence

between people and people walking in almost the

same elapsed time between cameras. Such assump-

tions may not be true in many practical situations. It

also requires people correspondences for all possible

pairs of cameras. Thus these algorithms also have the

computational complexity of O (N

), where N is the

camera number.

Considering the facts listed above, we believe that

the clothing color-based human re-identiﬁcation is

one of the most promising approaches. Thus im-

proving the color matching for this approach is very

important. For color matching problems, however,

the importance of distance metrics has not been em-

phasized enough: only simple distance metrics have

been exploited. Therefore in this paper, we propose

a method for learning optimal distance metrics be-

tween color histograms from different cameras. The

proposed method reduce the complexity of the BTF

from O (N

) to O (1), since it does not assume that

the camera conﬁguration is known. It is robust to

differences of color calibration between cameras as

well. To obtain better accuracy, we apply nonlinear

kernel functions to learn a nonlinear distance metric.

We experimentally validated the approach based on

the combination of large margin component analysis

(LMCA) and the Jensen-Shannon kernel. The pro-

posed method improves the identiﬁcation accuracy

for clothing color matching approach. Therefore, the

proposed method and many previous works are com-

plementary.

In summary the contribution of this paper is two-

fold: (a) the use of nonlinear distance metric learn-

ing is proposed to achieve better accuracy compared

with conventional simple distance metrics, and (b) the

combination of LMCA and the Jensen-Shannon ker-

nel function is proposed. The basic idea of the pro-

posed method is illustrated in Fig. 2(b) and compared

with the conventional methods shown in Fig. 2(a).

In contrast to the conventional methods that match

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

604

!"#$%&'

()*%!+,-"*

!"#$%&'

()*%!+,-"*

!"#$%&'

.)*%-/0&*

!$%#$%'1/-2'

*0!,&

(a)

!"#$%&'

()*%!+,-"*

!"#$%&'

()*%!+,-"*

!"#$%$&$'($!"#%)(*+"$,!%-!+#(,%($%&.($!

/&-01+!%

)(*+"$,!*%2(+3%

)(*+"$,!%-!+#(,%

4&$'($!"#%

5(*+"$,!%

-!+#(,%

.$%#$%'

*/!,&

(b)

Figure 2: (a) conventional and (b) proposed color matching

schemes.

clothing color histograms in a simple distance metric,

the proposed framework computes the distance with a

learned optimal distance metric.

The remainder of this paper is organized as fol-

lows. In Section 2, the proposed method is described

in depth with a review of some basic algorithms. In

Section 3 the experimental results are presented to

validate the proposed approach. Finally in Section 4,

concluding remarks are given.

2 PROPOSED METHOD

In this paper, we assume that the human region in a

camera view is given by a human detector or back-

ground subtraction algorithm. The training datasets

from many surveillance cameras under different con-

ditions and corresponding subject labels are assumed

available for metric learning. As mentioned above,

different cameras under different conditions cause

different color calibration. Hence the direct use of his-

tograms affects the identiﬁcation accuracy adversely.

In contrast, the optimal distance metric is learned with

a training dataset in the proposed work.

To learn the optimal metric, color histograms X =

;i = 1,...,n} are ﬁrstly computed for the train-

ing dataset, where n is the total number of training

samples in the dataset. Then using histograms X and

corresponding labels Y, the optimal distance metric

is learned. By including most of the possible vari-

ations in practical situations in the training dataset,

we expect this approach to work in real applications.

During the registration process, every time people en-

ter the ﬁelds of views of cameras, they are registered.

For each person, color histograms m

are extracted

as models. Denoting the number of people registered

as C, M = {m

;c = 1,...,C} are obtained. In the

re-identiﬁcation process, color histograms of test im-

ages, T = {t

;k = 1,... ,K} are obtained, where K is

the number of images to be matched. Histograms M

and T are matched using the learned distance metric.

In the proposed method, the large margin criterion

is used to learn the optimal distance metric. Nonlin-

ear projection φ(x

) is used to project the input his-

tograms onto a higher dimensional space. For non-

linear projection, several types of kernel functions are

investigated; the ﬁnal results are shown in experimen-

tal results section.

2.1 Clothing Color Histograms

Traditionally, color histograms are extracted in the

color spaces including RGB HSV, Lab, and YCbCr.

We use the HSV joint histograms in the HSV color

space because they showed better accuracy than other

color spaces according to our experiments. Since

clothing colors generally do not vary drastically

among front, back, right, and left views, for view-

point invariantmatching, vertical combination of such

clothing colors as the upper and lower body colors are

robust in many cases. Based on this observation, Bird

et al. (Bird et al., 2005) divided the entire human re-

gion into several vertically segmented regions to ob-

tain regional histograms. Following this scheme, in

this paper, the human region is segmented vertically

into P pieces, and for each sub-region p(p= 1,...,P),

HSV joint histograms x

∈ R

×b

are computed,

where b

are the number of bins in the H, S

and V color channels and x

is vectorized from the

2D joint histogram. Then to describe all the human

region features, these histograms in each region are

concatenated as x

= {x

,...,x

} ∈R

and normal-

ized so that

∑

| = 1, where D = b

×b

×P.

We apply this procedure for training, model, and test

images to obtain color histograms X, M, and T, re-

spectively.

HUMAN RE-IDENTIFICATION THROUGH DISTANCE METRIC LEARNING BASED ON JENSEN-SHANNON

KERNEL

605

2.2 Distance Metric Learning

Many supervised/unsupervised distance metric learn-

ing algorithms have been proposed (Yang, 2006). We

adopt a supervised learning algorithm in this work.

Among supervised algorithms, linear discriminant

analysis (LDA) is a major algorithm. However, LDA

has some limitations. For example, it cannot be ap-

plied when there are not enough data to estimate intra-

class scatter or insufﬁcient classes to make the be-

tween class scatter matrix be non-singular. On the

other hand, not only the linear distance metric but also

the nonlinear distance metric using kernel functions

have been proposed to improve accuracy. Among

them, the support vector machine (SVM) has gained

much popularity due to its good performance. How-

ever, since it was originally formulated as a binary

classiﬁcation problem, it cannot be applied directly

to multi-class problems. To extend the binary clas-

siﬁcation to the multi-class case, we can discrimi-

nate matching scores that share the same labels and

those between different labeled data. In the prac-

tice of this scheme, the number of differently la-

beled pairs often becomes extremely larger than that

of the pairs sharing the same labels, causing the un-

balanced training problem. To avoid this, sampling

is often adopted from a large number of differently

labeled pairs. However, there is no guarantee that

appropriate data can always be sampled, which may

cause over-ﬁtting. For these problems, Prosser et

al.(Prosser et al., 2010) proposed ensemble rankSVM

to solve this problem as ranking problem. Although

it shows good performance, it is noted that the tuning

of this algorithm is computationally expensive(Zheng

et al., 2011). To improve the ensemble RankSVM

further, recently Zheng et al.(Zheng et al., 2011) pro-

posed ”Probabilistic Relative Distance Comparison”

(PRDC), which is one of variants of distance metric

learning. This algorithm is promising, however, train-

ing process is still computationally expensive. On

the other hand, while a number of distance metric

learning have been proposed, the large margin near-

est neighbor (LMNN) (Weinberger and Saul, 2009) is

viewed as one of the best methods (Kulis, 2010) in

terms of accuracy. To further improve LMNN and al-

leviate the difﬁculties in processing high dimensional

data, Torresani et al. proposed large margin com-

ponent analysis (LMCA) (Torresani and Lee, 2007).

Furthermore, the algorithm was kernelized to learn

the distance metric in higher dimensional and non-

linear space for better performance. In this paper we

use it to learn the large margin distance metric. In the

following description, we brieﬂy review the algorithm

and describe how to apply it to the re-identiﬁcation

problem.

Linear LMCA:

Given color histogram features X = {x

;i =

1,...,n} ∈ R

D×n

and corresponding labels

Y = {y

;i = 1, ...,n} ∈ {0,1}

, LMCA minimizes

the following loss function ε(L):

ε(L) =

∑

||L(x

−x

)||

+ c

∑

ijl

(1−y

)

·h(||L(x

−x

)||

−||L(x

−x

)||

+ 1), (1)

where L ∈ R

d×D

is a linear projection for X, η

∈

{0,1} takes 1 iff x

and x

shares the same label

= y

) and x

is the k-nearest neighbor of x

, c > 0

is an appropriate balancing parameter, y

∈ {0,1} is

a variable that takes 1 iff y

= y

, and h(s) is a hinge

function that is deﬁned as h(s) = max(s,0). The ﬁrst

term minimizes projected distances between the data

pairs that share the same labels to encourage the in-

variance property, and the other term is for discrimi-

nation, which makes projected distances between the

data pairs with the same labels and those with dif-

ferent labels distant with unit distance 1. The hinge

function gives a loss for the invasive data and does

not affect those data that have enough margins. Opti-

mizing L by gradient descent based on this objective

function, optimal linear discriminative projection can

be obtained. Here the distance metric can be given by

Kernel LMCA:

For nonlinear projection φ(x

), the inner product is ex-

pressed as k(x

) = φ

. In subsequent descrip-

tion, the following notation is used: φ

= φ(x

)CΦ =

[φ

,...,φ

]

= Φφ

= [k(x

),...,k(x

)]. Us-

ing nonlinear projection, the loss function in the pro-

jected space is expressed as:

ε(L) =

∑

||L(φ

−φ

)||

+ c

∑

ijl

(1−y

)

·h(||L(φ

−φ

)||

−||L(φ

−φ

)||

+ 1). (2)

The gradient of the loss function becomes

∂ε(L)

∂L

∑

L(φ

−φ

)(φ

−φ

)

+ c

∑

ijl

(1−y

)

·h

′

ijl

)L[(φ

−φ

)(φ

−φ

)

−(φ

−φ

)(φ

−φ

)

], (3)

where

ijl

= ||L(φ

−φ

)||

−||L(φ

−φ

)||

+ 1. (4)

Considering the parameterizations of L as L = ΩΦ,

Eq. (3) yields

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

606

∂ε(L)

∂L

= 2Ω

∑

−k

)

−E

−k

)

]Φ

+ 2cΩ

∑

ijl

(1−y

′

ijl

)

·[E

−k

)

−E

−k

)

−E

−k

)

+ E

−k

)

]Φ, (5)

where

ijl

= {||Ω(k

−k

)||

−||Ω(k

−k

)||

+ 1}, (6)

= [0, . . . , 0,v,0,...,0] is a n ×n matrix that only

takes value v at the i-th column, and h

′

(s) is a dif-

ferential of h(s). To avoid the discontinuity of h

′

(s)

around 0, approximation by a smooth hinge function

was proposed(Rennie and Srebro, 2005). Using Eq.

(5), the steepest descent update rule is given by

L ← L−λ

∂ε(L)

∂L

. (7)

However in Eq. (5), all the terms in

∂ε(L)

∂L

have Φ and

L = ΦΩ by assumption, and Φ in Eq. (7) can be re-

moved. Hence the update rule is reduced to the fol-

lowing simple gradient descent update of Ω:

Ω ←Ω −λΓ, (8)

Γ = 2Ω

∑

−k

)

−E

−k

)

]

+ 2cΩ

∑

ijl

(1−y

′

ijl

)

·[E

−k

)

−E

−k

)

−E

−k

)

+ E

−k

)

]. (9)

By assumption, projection onto higher dimen-

sional space can be obtained easily:

Lφ

= ΩΦφ

= Ωk

. (10)

Here the distance metric can be represented as

Ω

Ωk

Since this algorithm automatically selects data

that fall within the margin through the learning pro-

cess, we expect better generalization compared to the

methods that sample ﬁxed pairs in advance, which is a

simple extension of the binary classiﬁcation problem

to the multi-class problem.

2.3 Kernel Functions

In this section, kernel functions that are suitable for

matching two distributions a,b ∈ R [0,1]

are inves-

tigated, such as normalized histograms or probability

distributions.

Histogram intersection kernel:

One popular distance between histograms is the his-

togram intersection. The histogram intersection ker-

nel, which satisﬁes Mercer’s condition, was proposed

in (Odone et al., 2005; Grauman and Darrell, 2005):

k(a, b) =

∑

min(a

). (11)

kernel:

Another popular distance between histograms is the

distance. Here, the χ

kernel function, satis-

ﬁes Mercer’s condition as well (Zhang et al., 2006;

Fowlkes et al., 2004). It is deﬁned as:

k(a, b) = exp











−



1−

∑

−b

)













. (12)

Bhattacharyya kernel:

Hellinger distance

∑



√

−

√



is effective be-

tween two probability distributions. Here a and b are

normalized histograms such that

∑

= 1,

∑

= 1,

and thus the distance yields 1 −

∑

√

, which is

called the Bhattacharyya distance. Based on the Bhat-

tacharyya distance, the following Bhattachayya ker-

nel is derived that satisﬁes Mercer’s theorem (Jebara

and Kondor, 2003):

k(a, b) =

∑

. (13)

Jeffrey divergence kernel:

In human re-identiﬁcation based on clothing color

histogram matching, one key point is that the ro-

bust matching between histograms is affected heav-

ily by noises. Due to the big appearance changes,

the shape of the color histograms are often altered,

which complicates robust matching. Thus we can-

not rely on histogram shape matching, while Gauss

kernel or other correlation-based kernels strongly rely

on histogram shape. For comparing and matching

such uncertain information, one popular way is an

information-based measure. For this problem, the

Kullback-Leibler divergence (KLD) H(a||b) is an ef-

fective measure of the differences between two prob-

abilistic pieces of information. However, due to its

asymmetry(H(a||b) 6= H(b||a)) the KLD cannot be

used directly as a kernel function. Symmetric Jeffrey

divergence (JD) H(a||b) + H(b||a)(Jeffreys, 1946) is

used to deﬁne the Jeffrey divergence kernel function

as exp(−JD/σ

). The deﬁnition is given by

k(a, b) = exp







−

∑



log

+ b

log









∏





















, (14)

HUMAN RE-IDENTIFICATION THROUGH DISTANCE METRIC LEARNING BASED ON JENSEN-SHANNON

KERNEL

607

where σ is another parameter that provides tuning

ﬂexibility. We don’t have proof for the positive def-

initeness of this kernel function yet, even though ex-

periments show that it is always positive deﬁnite.

Jensen-Shannon kernel:

Another way to circumvent KLD’s asymmetry is the

Jensen-Shannon divergence (JSD)(Lin, 1991). Not

only it is symmetric but it also has other numerous de-

sirable properties. As shown in (Huang et al., 2005),

it is numerically more stable than KLD or JD and pro-

vides a theoretical upper bound in terms of the vari-

ational distance; no general upper bound exists for

KLD or JD. Therefore the JSD-based kernel func-

tion, which satisﬁes Mercer’s theorem, is proposed

(Chan et al., 2004). To give one more parameter

σ for ﬂexibility, an exponential function is used as

exp(−JSD/σ

). The resulting kernel function is

k(a, b) = exp







−

∑



log









∏









+ b



2σ



+ b



2σ







. (15)

This kernel is positive deﬁnite (Chan et al., 2004).

Even though a variety of kernel functions exists, this

kernel has not received enough attention yet.

To investigate the effectiveness of this kernel for

our problem, a preliminary experiment using syn-

thetic data generated using Gaussian mixture model

is conducted. As shown in experimental section, we

use HSV joint histograms in the HSV color space. In

HSV joint histograms, hue, saturation and value com-

ponents can be easily shifted circularly by illumina-

tion changes or color calibration differences. To sim-

ulate data pairs from the same person, a pair of circu-

larly shifted and original distributions are used. For

data pairs from different persons, mutually different

distributions are used. An example of data pair is il-

lustrated in Fig.3. 500 samples of data pair is used to

draw a distribution of distances by each kernel. The

result can be shown in Fig.4. The distances between

data pairs with circular shift should be small, while

those between data pair with different distributions

should be large. To quantify the effectiveness, the ra-

tio of mean distance for simulated intra-person pairs

against that for simulated different individualpairs are

computed. The results can be seen in Table.1, where

the mean distance for simulated intra-person pairs is

denoted by m

shift

and that for simulated different in-

dividual pairs m

dif f

. The larger the ratio is, the better.

Viewing these results, we can see that the proposed

Jensen-Shannon kernel function is the most appropri-

ate for our HSV color space based matching problem.

2 4 6 8 10 12 14 16

0.05

0.1

0.15

0.2

0.25

0.3

0.35

distribution 1

dist.1 shifted circularly

distribution 2

Figure 3: Synthetic test distributions; the bold line and the

regular dotted line indicate a pair of color histograms of a

person from different cameras, which simulates circularly

shifted hue histogram in HSV color space, and the bold line

and the bold dotted line indicate a pair of color histograms

from different person.

0 0.5 1

100

120

140

Bhattacharyya kernel

0 0.5 1

100

hist. intersec. kernel

0 0.5 1

100

120

140

kernel

0 0.5 1

100

120

140

160

180

Jensen−Shannon kernel

Figure 4: Distance distribution in each kernel function; dot-

ted line indicates a distribution of distances between data

pairs with different color distributions, the other one indi-

cates a distribution of those between shifted and original

color distributions.

Table 1: Ratios of mean distance between shifted and orig-

inal data pairs against that between different data pairs.

Bhat. HI χ

shift

dif f.

1.8059 1.9113 2.0271 2.3351

2.4 Matching

Normalized color histograms are projected onto opti-

mized nonlinear space, as shown by Eq. (10), which

yields Ωk(X,M), Ωk(X, T), where Ω is learned by

Eq. (8), and X, M, and T are color histograms com-

puted from training dataset, model images, and test

images, respectively. Here matching can be done as:

= f(Ωk(X,m

),Ωk(X,t

)), (16)

where f(·, ·) is an arbitrary similarity function. Esti-

mated identity

for input data t

is given by taking

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

608

100

120

Figure 5: Subregion

division.

(a) Correct match: ID 126 (b) Correct match: ID 351 (c) False match: ID 006 & 135 (d) False match: ID 078 & 107

Figure 6: Successful and failure cases by the proposed method.

the maximum for similarity scores s with respect to

registered models M = {m

;c = 1,. . . ,C}:

= max

). (17)

Although any similarity function can be used as f in

Eq. (16), in the following experiments, we used cor-

relation.

3 EXPERIMENTS

We conducted experiments using the Viewpoint In-

variant PEdestrian Recognition (VIPeR) dataset by

Gray et al. (Gray and Tao, 2008) to show the ef-

fectiveness of the proposed method. This dataset

is constructed to evaluate viewpoint invariant human

re-identiﬁcation algorithms. Several examples from

VIPeR can be seen in Fig. 1. Due to the pose and

illumination variations, the clothing colors are signif-

icantly different between the two images of the same

person. Furthermore, in the dataset, the camera labels

are not available to indicate from which camera the

images were taken. Since estimating such color cali-

bration functions as BTF is impossible, this dataset is

quite difﬁcult for human re-identiﬁcation.

In this dataset, two images for each of 632 sub-

jects are included: one for the model and one for

matching. The training dataset is constructed by ran-

domly selecting 200 individuals from the 632 people.

Since there are two images for each subject, the train-

ing dataset has 400 images. The remaining 432 in-

dividuals are used for evaluation. In all experiments,

through ten cross validations, we estimated the mean

accuracy and the corresponding standard deviations.

In the human body extraction, if an automatic seg-

mentation algorithm was employed, the result would

be affected by its accuracy. To avoid this and evaluate

only the effect by difference of distance metrics, the

human body region is segmented manually. In prac-

tical situations, this can be done relatively easily by

background subtraction, for example.

Table 2: CMC in comparison.

CMC (1) CMC (10)

Baseline (Euclidean dist.) 8.7±0.8 24.2±1.0

Baseline (NCC) 10.8±1.0 28.6±0.8

Baseline (hist. intersec.) 13.2±1.1 35.3±1.0

Baseline (Bhat. dist.) 17.2±0.8 39.2±1.0

LMCA with lin. 13.0±1.0 37.3±2.4

LMCA with Gauss(5.0) 15.0±1.2 43.8±1.9

LMCA with hist. intersec. 17.1±2.4 51.1±2.3

LMCA with χ

19.6±1.5 53.6±1.5

LMCA with Bhat. 18.8±1.3 50.9±1.5

LMCA with JD 16.6±0.1 53.2±1.3

LMCA with JS 20.5±1.5 55.7±1.5

For feature extraction, we used HSV joint his-

togram in the HSV color space. We used ﬁve bins for

HS channels and three bins for V channel for quan-

tization. For division into sub-regions, the best ac-

curacy was given by segmentation into eight regions,

as illustrated in Fig. 5. The blue lines represent the

boundaries of each region and color histograms are

computed from the red areas in each sub-region. Con-

catenating these histograms in each image, we ob-

tained 5×5×3×8= 600 dimensional features.

We used a cumulative match characteristic (CMC)

curve to evaluate the matching performance. CMC (n)

represents the probability that correct matches appear

in the top n-th. CMC (1) and CMC (10), which rep-

resent the probability that correct matches are always

placed ﬁrst and within top 10 respectively, are shown

in Table 2. In the table, each cell includes estimated

mean value ± corresponding standard deviation. For

comparisons, such basic techniques as simple Eu-

clidean distance, normalized correlation, histogram

intersection, and Bhattacharyya distance are listed as

baselines. In the LMCA evaluation, in addition to lin-

ear LMCA, we tested various kernel LMCAs, includ-

ing Gauss, histogram intersection, χ

, Bhattacharyya,

Jeffrey divergence, and Jensen-Shannon kernels. The

combination of LMCA and the Jensen-Shannon ker-

nel gave the best result. On the other hand, for the

HUMAN RE-IDENTIFICATION THROUGH DISTANCE METRIC LEARNING BASED ON JENSEN-SHANNON

KERNEL

609

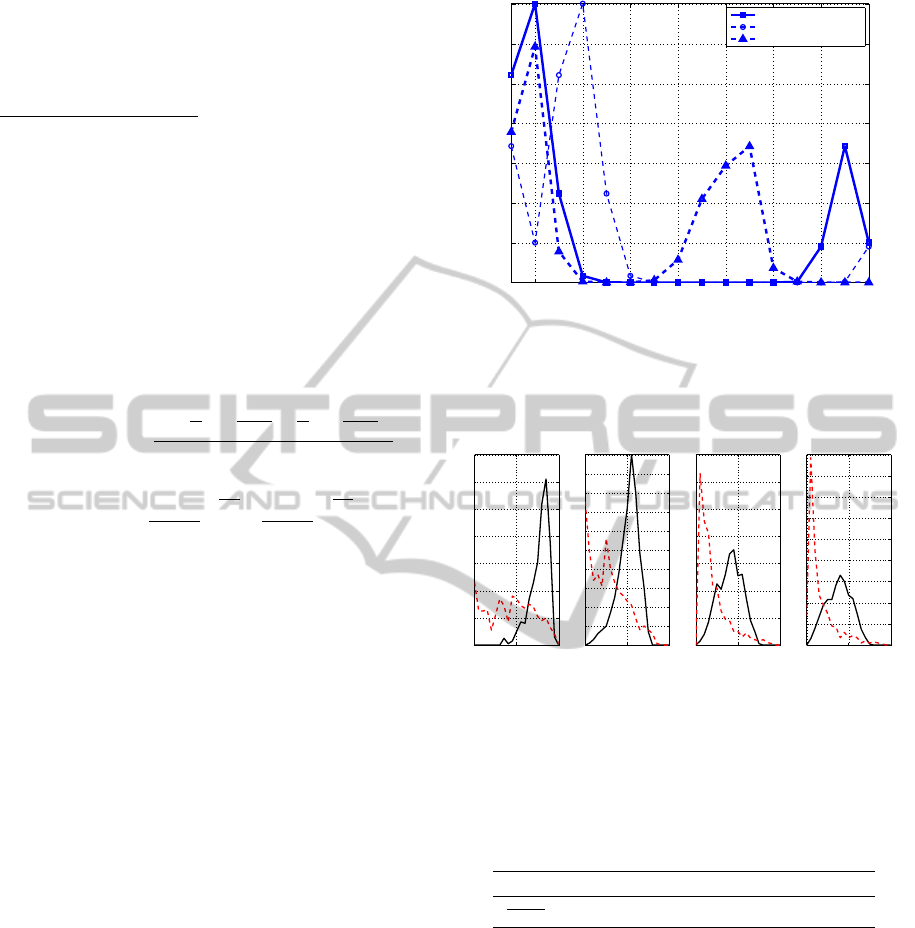
0 50 100 150 200 250 300 350 400 450

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Cumulative Match Characteristics

Rank

Recognition rate

LMCA(JS)

LMCA(χ

)

LMCA(Bhat.)

LMCA(Gauss)

Bhat.

NCC

Figure 7: CMC curve.

Gauss kernel, the accuracy was degraded compared

to the simple distances, which means it is unsuitable

for matching normalized histograms. Moreover, the

result from LMCA plus the Jensen-Shannon kernel is

better than that from the PRDC(Zheng et al., 2011),

which can achieve 12.64% for CMC(1) and 44.28%

in CMC(10) in equivalentdata setup described in their

paper. Considering in (Zheng et al., 2011) 29 dif-

ferent feature channels such as Schmid and Gabor

ﬁlter for RGB, YCbCr, HSV color spaces are used,

the proposed method which uses only HSV joint his-

tograms is much more efﬁcient and probably faster in

re-identiﬁcation process.

The summarizing CMC curve is shown in Fig.

7. The proposed method (LMCA with the Jensen-

Shannon kernel) is the best for all ranks. Some suc-

cessful and failure examples by the proposed method

are shown in Figs. 6(a)-(d). Although the appearances

are quite different, for pairs in (a) and (b) from the

same ID, the proposed method effectively absorbed

the differences. However, pairs in (c) and (d) from

different IDs are falsely ranked ﬁrst by the proposed

method. For the images in the pair (c), roughly speak-

ing, the only difference is the facial skin color, and

most of body region is the same color. This kind of

cases is still critical in the proposed method. The

other failure case in the pair (d), the only difference

is the upper body color. In addition, the upper body

region is including the same color. Presumably it is

due to the limitation of using histogram without spa-

tial information. Some extent of spatial ambiguity

is required for viewpoint invariance, so it is a trade-

off problem. Although seeking better features is out-

side the scope of this paper, more representative fea-

tures would give better accuracy using the proposed

method for these cases.

Finally we experimented with SDALF(Farenzena

et al., 2010), which is one of the current state-of-the-

Table 3: Combination with state-of-the-art algorithm.

CMC (1) CMC (10)

(a) SDALF (wHSVhist) 9.8±0.5 28.2±1.7

(b) SDALF (MSCR) 7.8±0.7 23.2±0.8

(a) + (b) 14.7±1.1 41.1±1.6

LMCA(JS) + (b) 21.3±1.2 57.7±2.6

art algorithm. The results are shown in Table 3. All

the experimental setups are the same as mentioned

above. The ﬁrst three lines show the accuracy when

only the color features (MSCR, weighted HSV his-

tograms, and their combination) are exploited. Since

the proposed algorithm can be seen as an alternative

to weighted histogram matching, we used our pro-

posed method with MSCR. The results are in the last

line. The SDALF performance drastically improved

by only replacing the histogram matching part from

the original weighted histogram matching to the pro-

posed nonlinear distance metric learning-based his-

togram matching.

The result shows the top level accuracy on VIPeR

with the advantage of only using color features and so

fast processing. This suggests the effectiveness of the

proposed method.

The kernel LMCA learning took about 80 [sec]

with 400 training datasets

. Thus given a sufﬁcient

number of training datasets, the algorithm can learn

optimal distance metrics relatively quickly. Com-

pared to the color calibration between cameras (such

as BTF) or inter-camera relationship modeling that re-

quires optimization for each pair of cameras, in the

proposed method, optimization can be done just once

at setup. Thus while BTF has computational com-

plexity of O (N

) w.r.t number of cameras N, that of

the proposed method is just O (1). Therefore the pro-

posed method is especially easy to implement when a

large number of cameras are employed.

4 CONCLUSIONS

In this paper, we study the human re-identiﬁcation

problem based on clothing colors. The re-

identiﬁcation approach based on distance metric

learning is validated experimentally. The combina-

tion of LMCA and the Jensen-Shannon kernel pro-

vided the best accuracy in our experiments.

The proposed method does not assume that the

camera conﬁguration is known. Our approach is dif-

ferent from the brightness transfer function estimation

The other experimental environments included Matlab

unoptimized code on Mac OS X, Core2Duo 2.2 GHz with

2GB memory.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

610

or inter-camera relationship modeling, where some

amount of the exact human correspondences in each

pair of cameras are needed. Therefore the advantage

of the proposed approach lies in the computational ef-

ﬁciency, which becomes obvious when a large num-

ber of cameras are deployed.

REFERENCES

Alahi, A., Vandergheynst, P., Bierlaire, M., and Kunt,

M. (2010). Cascade of descriptors to detect and

track objects across any network of cameras. CVIU,

114(6):624–640.

Bak, S., Corvee, E., Br´emond, F., and Thonnat, M. (2010).

Person Re-identiﬁcation Using Spatial Covariance

Regions of Human Body Parts. In Proc. of AVSS.

Bazzani, L., Cristani, M., Perina, A., Farezena, M.,

and Murino, V. (2010). Multiple-shot Person Re-

identiﬁcation by HPE signature. In Proc. of ICPR.

Berdugo, G., Soceanu, O., Moshe, Y., Rudoy, D., and Dvir,

I. (2010). Object Reidentiﬁcation in Real World Sce-

narios Across Multiple Non-overlapping Cameras. In

Proc. of Euro. Sig. Proc. Conf.

Bird, N. D., Masoud, O., Papanikolopoulos, N. P., and

Isaacs, A. (2005). Detection of Loitering Individuals

in Public Transportation Areas. IEEE Trans. on ITS,

6(2):167–177.

Chan, A., Vasconcelos, N., and Moreno, P. (2004). A fam-

ily of probabilistic kernels based on information di-

vergence. Univ. of California, San Diego, Tech. Rep.

Farenzena, M., Bazzani, L., Perina, A., Murino, V., and

Cristani, M. (2010). Person Re-Identiﬁcation by

Symmetry-Driven Accumulation of Local Features. In

Proc. of CVPR.

Fowlkes, C., Belongie, S., Chung, F., and Malik, J. (2004).

Spectral grouping using the Nystr¨om method. IEEE

Trans. on PAMI, 26(2):214–225.

Gheissari, N., Sebastian, T. B., and Hartley, R. (2006). Per-

son Reidentiﬁcation Using Spatiotemporal Appear-

ance. In Proc. of CVPR.

Gilbert, A. and Bowden, R. (2006). Tracking Objects

Across Cameras by Incrementally Learning Inter-

camera Colour Calibration and Patterns of Activity. In

Proc. of ECCV.

Grauman, K. and Darrell, T. (2005). The Pyramid Match

Kernel: Discriminative Classiﬁcation with Sets of Im-

age Features. In Proc. of ICCV.

Gray, D. and Tao, H. (2008). Viewpoint Invariant Pedestrian

Recognition with an Ensemble of Localized Features.

In Proc. of ECCV.

Hamdoun, O., Moutarde, F., Stanciulescu, B., and Steux,

B. (2008). Person re-identiﬁcation in multi-camera

system by signature based on interest point descrip-

tors collected on short video sequences. In Proc. of

ICDSC.

Hirzer, M., Beleznai, C., Roth, P. M., and Bischof, H.

(2011). Person Re-identiﬁcation by Descriptive and

Discriminative Classiﬁcation. In Scandinavian Con-

ference on Image Analysis, pages 91–102.

Huang, T. and Russell, S. (1997). Object identiﬁcation in

a Bayesian context. In Proc. of Joint Conf on AI &

IJCAI.

Huang, X., Li, S. Z., and Wang, Y. (2005). Jensen-shannon

boosting learning for object recognition. In Proc. of

CVPR.

Javed, O., Shaﬁque, K., Rasheed, Z., and Shah, M. (2008).

Modeling inter-camera space-time and appearance re-

lationships for tracking across non-overlapping views.

CVIU, 109(2):146–162.

Jebara, T. and Kondor, R. (2003). Bhattacharyya and Ex-

pected Likelihood Kernels. In Proc. of Comp. Learn.

Theory.

Jeffreys, H. (1946). An invariant form for the prior proba-

bility in estimation problems. A Math. and Physical

Sciences, 186(1007):453–461.

Kulis, B. (2010). ICML 2010 Tutorial on Metric Learning.

Kuo, C.-H., Huang, C., and Nevatia, R. (2010). Inter-

camera Association of Multi-target Tracks by On-Line

Learned Appearance Afﬁnity Models. In Proc. of

ECCV.

Lin, J. (1991). Divergence measures based on the Shannon

entropy. IEEE Trans. on Info. Theory, 37(1):145–151.

Lin, Z. and Davis, L. S. (2008). Learning Pairwise Dissim-

ilarity Proﬁles for Appearance Recognition in Visual

Surveillance. In Proc. of ISVC.

Odone, F., Barla, A., and Verri, A. (2005). Building kernels

from binary strings for image matching. IEEE Trans.

on Image Proc., 14(2):169–180.

Pasula, H., Russel, S. J., Ostland, M., and Ritov, Y. (1999).

Tracking many objects with many sensors. In Proc. of

IJCAI.

Prosser, B., Gong, S., and Xiang, T. (2008a). Multi-camera

Matching under Illumination Change Over Time. In

Proc. of Workshop on Multi-camera and Multi-modal

Sensor Fusion Algorithms and Applications.

Prosser, B., Gong, S., and Xiang, T. (2008b). Multi-camera

Matching using Bi-DirectionalCumulative Brightness

Transfer Functions. In Proc. of BMVC.

Prosser, B., Zheng, S., Gond, S., and Xiang, T. (2010). Per-

son Re-Identiﬁcation by Support Vector Ranking. In

Proc. of BMVC.

Rennie, J. D. M. and Srebro, N. (2005). Fast maximum

margin matrix factorization for collaborative predic-

tion. In In proc. of ICML.

Schwartz, W. R. and Davis, L. S. (2009). Learning Discrim-

inative Appearance-Based Models Using Partial Least

Squares. In Proc. of Brazil. Symp. on Comp. Graph.

and Image Proc.

Slawormir, B., Corvee, E., Br´emond, F., and Thonnat, M.

(2011). Multiple-shot Human Re-Identiﬁcation by

Mean Riemannian Covariance Grid. In Proc. of AVSS,

pages 179–184.

Song, B. and Roy-Chowdhury, A. K. (2007). Stochastic

Adaptive Tracking In A Camera Network. In Proc. of

ICCV.

Torresani, L. and Lee, K.-c. (2007). Large margin compo-

nent analysis. NIPS.

Wang, X., Doretto, G., Sebastian, T., Rittscher, J., and Tu,

P. (2007). Shape and Appearance Context Modeling.

In Proc. of ICCV.

HUMAN RE-IDENTIFICATION THROUGH DISTANCE METRIC LEARNING BASED ON JENSEN-SHANNON

KERNEL

611

Weinberger, K. Q. and Saul, L. K. (2009). Distance Metric

Learning for Large Margin Nearest Neighbor Classi-

ﬁcation. JMLR, 10:207–244.

Yang, L. (2006). Distance metric learning: A comprehen-

sive survey. Michigan State Univ. Tech. Report.

Zhang, J., Marszalek, M., Lazebnik, S., and Schmid, C.

(2006). Local Features and Kernels for Classiﬁcation

of Texture and Object Categories: A Comprehensive

Study. IJCV, 73(2):213–238.

Zheng, W.-S., Gong, S., and Xiang, T. (2011). Person Re-

identiﬁcation by Probabilistic Relative Distance Com-

parison. In Proc. of CVPR.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

612