TEXTURE IMAGE ANALYSIS USING LBP AND DATA

COMPRESSION

Nuo Zhang and Toshinori Watanabe

Graduate School of Information Systems, the University of Electro-Communications,

1-5-1, Chofugaoka, Chofu-shi, Tokyo, Japan

Keywords:

Data Representation, Texture Image, Data Compression, Local Binary Patterns.

Abstract:

Texture classiﬁcation is an important technology widely applied in many application ﬁelds in image process-

ing. In this study, a novel representation method for texture image is proposed. The proposed approach is

based on the consideration of using data compression to search the essential feature of frequent pattern in

texture images. Furthermore, to deal with the difﬁcult situation caused by different situations of photography,

local binary pattern (LBP) is introduced to the proposed approach to reduce the numbers of varieties of pat-

terns in texture image. Compresibility vector space is adopted in this study instead of learning phase. Based

on the patterns extracted by LBP operator which are invariant to monotonic gray-level transformations, data

compression helps extract the longest and frequent features. These features provide high analytical ability for

texture image. The simulation results will show good performance of our approach.

1 INTRODUCTION

Textures, such as the surface of wood and rock gener-

ally appear in most images in real world. The related

algorithms for texture analysis have been broadly

studied so far. Exact feature expression of texture im-

age will help to improve the performance in image

processing.

A lot of methods for the analysis of texture im-

age have been proposed. Hu Chun-hai et al. fo-

cused on the analysis of wood surface inspection to

wood machining industries (Hu and Liang, 2008).

They presented an efﬁcient image restoration scheme

in wavelet domain and defect detection approach for

texture image. Retrieval of texture image attracts

researchers and a lot of results have been emitted.

Ying Liu et al. proposed a image retrieval method

based on texture segmentation in wavelet domain (Liu

et al., 2003). And this method showed promising re-

trieval performance based on texture features. Fauzi,

M.F.A. et al. presented a robust technique for texture-

based image retrieval in multimedia museum collec-

tions (Lewis, 2003). And the results showed that the

multiscale sub-image matching method is an efﬁcient

way to achieve effective texture retrieval without any

segmentation. Smith, J.R. et al. proposed a new al-

gorithm for the automated extraction and indexing

of salient image features based on texture features

(Smith and Chang, 1996). Suzuki, M.T. et al. used

Laws’ texture energy measure technique to analyze

texture image (Suzuki et al., 2009). They used multi-

ple resolutions of ﬁlters to make it possible to extract

various image features from 2D texture images of a

database. In texture analysis, a difﬁcult problem is

that textures are often not uniform, due to changes in

monotonic gray-level, orientation, scale or other vi-

sual appearance.

In this study, a new representation method for tex-

ture image based on the combination of local binary

patterns (LBP) (Ojala et al., 2002) and data com-

pression is introduced. The proposed approach can

ﬁnd long and frequent patterns, which are invariant

to monotonic gray-leveltransformations, from texture

images and use shorter symbols to replace them. This

manner suggests that the proposed approach is able to

be used as a effective method for texture image repre-

sentation. The performance of the proposed approach

will be shown in experiments.

2 IMAGE REPRESENTATION

USING LBP OPERATOR AND

DATA COMPRESSION

In this study, we attempt to build a feature space

(compressibility space) to represent texture images

appreciatively. We ﬁrst convert the input texture im-

437

Zhang N. and Watanabe T..

TEXTURE IMAGE ANALYSIS USING LBP AND DATA COMPRESSION.

DOI: 10.5220/0003850904370440

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 437-440

ISBN: 978-989-8565-03-7

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

ages to ones which are robust to monotonic gray-level

transformations. Then, some images are randomly

selected to build a feature space. The ﬂow chart is

shown in Fig. 1.

In general, a model of input information source

is used for encoding the input stream in data com-

pression. And a compression dictionary is used as the

model. The compression dictionary is automatically

produced when compressing input data, eg. Lempel-

Ziv (LZ) compression (Ziv and Lempel, 1978). In the

same way, the proposed approach constructs a com-

pression dictionary by encoding input data forms. It

makes a compressibility vector space from the com-

pression dictionary to project new input data into it.

Therefore, we can get the feature of data represented

by a compressibility vector. Finally, input data are

classiﬁed by analyzing these compressibility vectors.

Figure 1: Representation of image based on LBP and data

compression.

To avoid the effect of monotonic gray-level trans-

formations in real world texture images, local binary

pattern (LBP) (Ojala et al., 2002) is employed in

the proposed approach before the construction of the

compressibility space. It is considered to be invari-

ance against monotonicgray-leveltransformations af-

ter an image is processed by LBP.

2.1 Local Binary Pattern

The LBP operator was originally developed for tex-

ture description (Ojala et al., 2002). It assigns each

pixel a binary value in comparison with the center

pixel intensity in a local neighborhood. If the gray-

level of a neighboring pixel is equal to or larger than

that of the central pixel, the value of that pixel is set

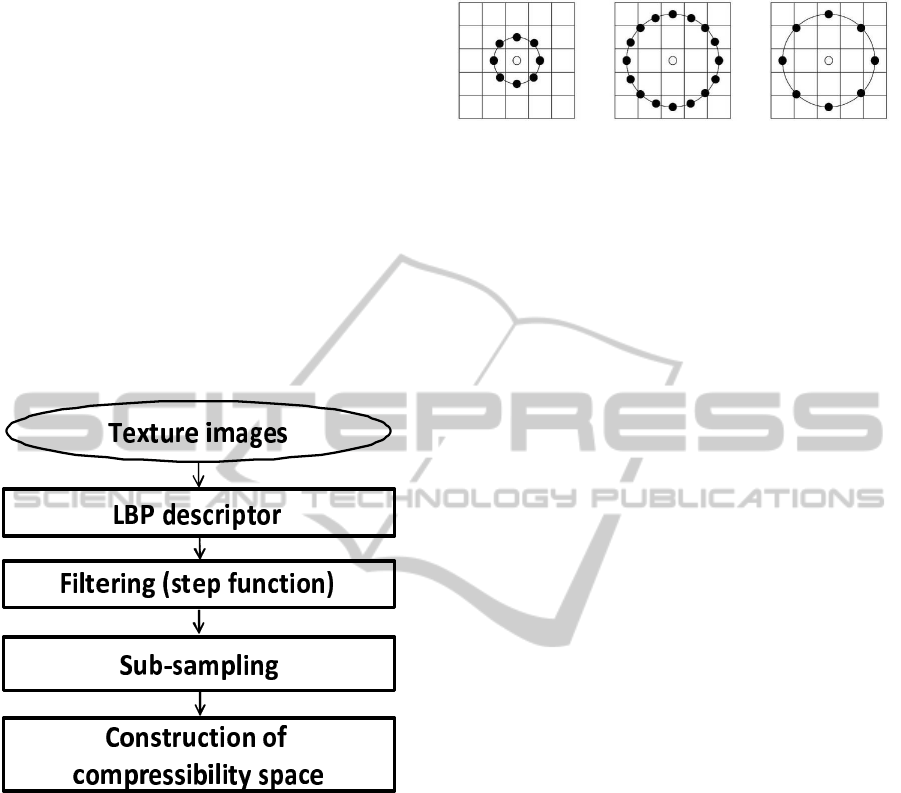
Figure 2: The circular (8,1), (16,2), and (8,2) neighbor-

hoods. The pixel values are bilinearly interpolated when-

ever the sampling point is not in the center of a pixel.

to one, otherwise zero. Then, LBP operator sums up

the value of neighborhood:

LBP

(x, y) =

P−1

∑

i=0

s(p

− p

, s(x) =



0,x<0

1,x≥ 0

(1)

where p

corresponds to the gray-level of the center

pixel of a local neighborhood, and p

corresponds to

the gray-levels of P sampled pixels on a circle of ra-

dius R. The notation (P, R) stands for pixel neighbor-

hood which means P sampling points on a circle of

radius R. Since correlation between pixels decreases

when distance increases, most texture informationcan

be obtained from local neighborhood. Thus, the ra-

dius R is usually kept small.

Then, the histogram of the processed image is

investigated instead of original texture image (Fig.

2). During which, bilinear interpolation is used when

sampling points do not fall in the middle of a pixel.

See Fig. 2 for examples of circular neighborhoods.

According to the robustness to monotonic gray-

level transformations of LBP descriptor, we employ

LBP descriptor before the construction of compress-

ibility vector space. For effectively representing fea-

tures in a texture image, the image result processed

by LBP descriptor instead of LBP histogram, is used

in this study. In comparison with the original image,

there are fewer but normalized patterns in the image

result processed by LBP descriptor. These patterns

helped to ﬁnd the same features between two pho-

tos of one person’s face took in different time periods

and showed high representing performance. Instead

of histograms used in original LBP method, the im-

age results processed from LBP descriptor are then

used to construct a feature space.

2.2 PRDC-based Image Representation

The proposed approach for image representation is

described as follows. The ﬂow chart is shown in Fig.

Each image is processed by LBP operator. The

image consists of local binary patterns is ﬁltered by a

step functionand pixel sub-sampling, in consideration

of the computation cost for the following processing.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

438

In this study, grayscale images are used in the exper-

iments. All the images are changed to 256 grayscale

in a pre-process step. Then a step function is used on

these grayscale images to reduce the 256 gradation

into 16. And the m× n image is converted to a 1× mn

vector. Text compression is used by PRDC (Pattern

Representation Scheme using Data Compression) to

ﬁnd most frequently repeated and longest feature in

text data. In order to adopt this advantage of PRDC,

images converted to text data. But the size of image

data is too big to directly convert each pixel to a char-

acter. Besides that the extracted features will become

too much and some of which are redundancy. Hence,

we consider dividing a 1 × mn vector segments and

cluster them. After which, each cluster is replaced

by a character and the converted image is called text-

transformed image. To obtain the text-transformed

images, data compression is then used for representa-

tion of the converted texture image in this study. Each

1× mn vector (of a grayscale image) is made into seg-

ments with length L. The PRDC is used to compress

the segments into compressibility vectors. The dictio-

naries used for compression are constructed by com-

pressing the pre-processed images with LZW method,

from a small number of randomly chosen images.

On these compressibility vectors, clustering with

k-means is performed to get clusters of segments. It

is considered that the segments belong to the same

cluster have similar properties. Therefore we can re-

place them by one character, from which we get the

text-transformed image.

Now we classify the text-transformed images

based on the PRDC. The PRDC is used again to com-

press the text-transformed image to obtain compress-

ibility vectors. And the dictionary is constructed by

compressing the text-transformed image with LZW

method. In the same way, clustering is performed on

the compressibility vectors. The compressibility vec-

tors are used as follows for classiﬁcation of similar

texture image. The compression dictionaries consti-

tute a compressibility vector space. The compressibil-

ity vector space can be represented by a compressibil-

ity table, which is made by projecting the input data

into the compressibility vector space. Let N

be the

input data. By compressing the input data, a com-

pression dictionary is obtained, which is expressed as

. Compressing data N

by D

, we get compres-

sion ratio C

. Where, L

is the size of the

input stream N

, K

is the size of the output stream.

Compressing with all of the dictionaries, we obtain a

compressibility vector for each input and for all input

data we get a compressibility table. In this table, the

columns show the data N

, the rows show the com-

pression dictionary D

formed by the same data, and

the elements show the compressibilityC

[%]. We

utilize this table to characterize data. Finally, images

are classiﬁed by the proposed approach.

3 EXPERIMENTS AND RESULTS

In this section, we show how to evaluate the perfor-

mance of the proposed approach. Experiments with

using real-world images were carried out. When eval-

uating a texture image analysis method, a number of

aspects such as change in rotation and scale should

be considered. The performance evaluation of our

approach is implemented in the following different

cases. Based on the experiences of the authors, R = 3

is used for the radius and P = 8 pixels are used for

the sampling points in LBP operator, in which it rep-

resents the texture images well.

3.1 Rotation Invariance

For the case of rotation invariance, we test if our ap-

proach can cope with the rotation of the image change

with respect to the viewpoint.

Figure 3: Examples of texture images in (Lazebnik et al.,

2005).

We randomly select 5 unrotated and 5 rotated im-

ages from all 25 texture classes (Fig. 3) in textured

surfaces to obtain 250 images. Then the proposed

approach is applied to express these images, and the

value of recall of clustering is computed. Because the

initialization value of k-means gives inﬂuence on the

experiments, this experiment runs 5 times to obtain

the average recall. As the result, the average recall

reached to 89 percent, which is close to the results

(88.1 to 92.6 percent) obtained in (Lazebnik et al.,

2005). The average recall got by only using data

compression representation is 72 percent. This result

showed that our approach is able to deal with the case

when images changed in rotation.

Though images changed in rotation, the combi-

nation of LBP operator and data compression rep-

resentation was able to ﬁnd out frequent patterns

when textures appear in images repeatedly. Hence

TEXTURE IMAGE ANALYSIS USING LBP AND DATA COMPRESSION

439

our approach may extract frequent pattern for images

changed in rotation.

3.2 Texture Image Clustering

For testing the representation performance, we also

evaluated if our approach can separate textures

from many different groups extracted from Brodatz

database (Fig. 4).

Figure 4: Examples from Brodatz database.

The Brodatz database consists of 111 images.

They are formed into classes by partitioning each im-

age into nine nonoverlapping fragments, for a total of

999 images. Fragment resolution is 213 × 213 pixels.

We randomly select 10 different textures in Bro-

datz database to get 90 images. The proposed ap-

proach is applied to separate these images. For the

same reason described previously, this experiment

runs 10 times to compute average recall. And the av-

erage recall reached to 92.6 percent. It was 83 per-

cent when only using data compression representa-

tion. Compared to the results (49.3 to 87.2 percent)

in (Ojala et al., 2002), this result showed that our

approach was applicable to represent images in Bro-

datz database. Although larger number of images in

more complicated situation were used in (Ojala et al.,

2002), the learning (or training) step is not necessary

in our proposed approach.

4 CONCLUSIONS

In this study we introduced a texture image represen-

tation method based on the combination of LBP oper-

ator and data compression, in which the training step

is not necessary. We evaluated the representation per-

formance of our approach under the consideration of

texture image changes in rotation. The experiments

were implemented with both Brodatz database and

textured surfaces. Our approach showed good perfor-

mance in the experiments. Its effectiveness shows its

potential applicability to other application of texture

image analysis. The future work includes the com-

parison with other methods using large-scale dataset.

REFERENCES

Hu, C. and Liang, H. (2008). Wood surface texture in-

spection using automatic selection band for wavelet

reconstruction. Proceedings of the SPIE - The Interna-

tional Society for Optical Engineering, 7130:713038–

713038–7.

Lazebnik, S., Schmid, C., and Ponce, J. (2005). A sparse

texture representation using local afﬁne regions. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, 27(8):1265–1278.

Lewis, M. F. P. (2003). Texture-based image retrieval us-

ing multiscale sub-image matching. Proceedings of

the SPIE - The International Society for Optical Engi-

neering, 5022:407–416.

Liu, Y., Wu, S., and Zhou, X. (2003). Texture segmenta-

tion based on features in wavelet domain for image

retrieval. Proceedings of the SPIE - The International

Society for Optical Engineering, 5150(1):2026–2034.

Ojala, T., Pietikainen, M., and Maenpaa, T. (2002). Mul-

tiresolution gray-scale and rotation invariant texture

classiﬁcation with local binary patterns. Pattern Anal-

ysis and Machine Intelligence, IEEE Transactions on,

24(7):971–987.

Smith, J. and Chang, S.-F. (1996). Automated binary tex-

ture feature sets for image retrieval. IEEE Interna-

tional Conference on Acoustics, Speech, and Signal

Processing Conference Proceedings, 4:2239–2242.

Suzuki, M., Yaginuma, Y., and Kodama, H. (2009). A 2d

texture image retrieval technique based on texture en-

ergy ﬁlters. IMAGAPP 2009. First International Con-

ference on Imaging Theory and Applications, pages

145–151.

Ziv, J. and Lempel, A. (1978). Compression of in-

dividual sequence via variable-rate coding. IEEE

Trans.Inf.Theory, IT-24, (5):530–536.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

440