REVERSE SUBDIVISION FOR OPTIMIZING VISIBILITY TESTS
Troy F. Alderson and Faramarz F. Samavati
Department of Computer Science, University of Calgary, 2500 University Drive, Calgary, Canada
Keywords:
Terrain Simplification, Line of Sight, Reverse Subdivision.
Abstract:
Certain applications require knowledge of whether two entities are visible to each other over a terrain, deter-
mined using a line-of-sight computation. Several fast algorithms exist for terrain line-of-sight computations.
However, performing numerous line-of-sight computations, particularly over a large terrain data set, can be
highly resource-intensive (in run time and/or memory). Methods from the field of terrain simplification can be
used to reduce the resource impact of the visibility algorithms. To take advantage of the especially fast algo-
rithms that exist for regular terrain models, we introduce regularity-preserving terrain simplification methods
based on reverse subdivision, including a novel reverse subdivision algorithm designed to maximize visibility
test accuracy, and compared the resulting visibility test output to several terrain simplification methods. Ad-
ditionally, the positions of the entities after simplification can have a significant impact on the visibility test
results. Hence, we have experimented with different functions that change the positions of the test points in
an attempt to maximize visibility test accuracy after simplification.
1 INTRODUCTION
In many computer graphics applications, such as
flight simulations and geographic information sys-
tems (GIS), a digital representation of a terrain is re-
quired. In general, digital terrain models are divided
into two types: digital elevations models (DEMs),
which are regular grids of elevations values; and tri-
angulated irregular networks (TINs), which are irreg-
ular polygonal meshes composed of triangles (Duven-
hage, 2009). These terrain models can become very
large and detailed, especially for large areas.
However, due to their regular structure, DEMs
benefit from lower memory usage than TINs (since
connectivity is implicit) and faster/easier data access.
These features of DEMs make for very fast line-
of-sight computations (or visibility test algorithms)
when compared against TINs (Seixas et al., 1999).
In several applications (such as military battle-
field simulations and radio transmission tower place-
ment), line-of-sight computation is an important oper-
ation. Terrain line-of-sight computation involves test-
ing whether the sight line between a pair of objects
(or points) intersects, and is thus obstructed by, a ter-
rain. Computing the visibility information between a
set of n points requires O(n
2
) visibility tests. If the in-
dividual visibility tests are resource-intensive, which
can happen when the terrain is large, then the cost of
this computation can drop below real time levels.
In the interest of optimizing the resource usage of
visibilty test algorithms, we have considered reducing
the size of the terrain using methods from the widely
studied field of terrain simplification. As regular ter-
rains feature both low memory usage and fast visibil-
ity algorithms, it is particularly desirable to preserve
regularity in the simplification process.
An easy way to achieve regularity preservation
in a terrain simplification scheme is to begin with a
curve simplifying scheme and apply it to the rows and
columns of the regular terrain. A suitable curve sim-
plification scheme would need to ensure that curves
with equal numbers of points before simplification
will still have equal numbers of points after simplifi-
cation, otherwise it will be impossible to connect the
curve points in a regular manner. Additionally, DEM
data points are often equally spaced along two di-
mensions, allowing the terrain to be specified almost
entirely using only the data for the third dimension
(i.e. the elevation values). Though not required, the
curve simplification scheme should maintain or ap-
proximate this equal spacing between the data points.
A regular surface simplification scheme satisfy-
ing these requirements is reverse subdivision. For-
ward subdivision introduces new points into a surface
in some predictable manner. Reverse subdivision,
an approximate inverse of this process, simplifies a
143
F. Alderson T. and F. Samavati F..
REVERSE SUBDIVISION FOR OPTIMIZING VISIBILITY TESTS.
DOI: 10.5220/0003851501430150
In Proceedings of the International Conference on Computer Graphics Theory and Applications (GRAPP-2012), pages 143-150
ISBN: 978-989-8565-02-0
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

surface in some predictable manner. We have stud-
ied several reverse subdivision schemes to achieve
regularity-preserving terrain simplification, including
a novel algorithm that uses least squares error mini-
mization to preserve the spatial relationships between
feature-critical points.
In general, a simplified terrain cannot perfectly
approximate the original, hence changes in the ter-
rain’s shape are inevitable. Therefore, it is also im-
portant to preserve the results of the visibility test.
We have compared our reverse subdivision meth-
ods against several irregular simplification methods to
guage their effectiveness at preserving test accuracy.
Aside from the terrain shape, the positions of the
test points also have an effect on the visibility test re-
sults. After the terrain model is simplified, the test
points are usually projected onto the simplified ter-
rain. However, while mathematically sound, trans-
forming the point positions in this way may not be
the best choice for maximizing visibility test accu-
racy. Hence, this work also compares transformations
of the test points, or “point relocation functions”, in
their ability to preserve the visibility test results.
Related work is given in Section 2. In Section 3
we describe the problem examined in this work. Sec-
tions 4 and 5 describe the simplification algorithms
and point relocation functions, respectively, that we
have tested. Finally, our comparisons between the
reverse subdivision schemes and several non-regular
simplification methods may be found in Section 6.
2 RELATED WORK
There are several versions of the visibility problem:
point visibility, line visibility, and region visibility.
(De Floriani and Magillo, 1993) describes these visi-
bility problems and some solutions to them. Our work
focuses on point-to-point visibility, although we sus-
pect it would prove useful in the other cases.
Several fast algorithms have been developed for
point-to-point line-of-sight computations over DEMs
and TINs. Bresenham’s line algorithm (Bresenham,
1965), used to plot a line on a raster grid, can be
adapted for DEMs to traverse the path of a sight line
and compare elevation values along that path. The
algorithm is linear in the number of elevation values
that lie along the sight line’s path.
Spatial subdivision can be used to produce an
asymptotically faster algorithm. (Duvenhage, 2009)
uses an implicit min/max k-d tree to quickly cull re-
gions of the terrain that lie completely under or over
the sight line to obtain an algorithm that is logarith-
mic in the number of elevation values that lie along
the sight line’s path, on average.
The implicit connectivity of regular models allows
for efficient storage, addressing, and access of data
values. This would suggest that visibility algorithms
over DEMs should be computationally more efficient
than visibility algorithms over TINs. Evidence sug-
gests that this is so. (Seixas et al., 1999) compared the
run time of the Bresenham line algorithm for DEMs
against an R3-tree algorithm for TINs, and found the
Bresenham algorithm to be substantially faster with a
smaller memory footprint.
However, these visibility algorithms do not ad-
dress the issue of the terrain size, which is a key factor
in their performance and/or memory usage. In (An-
drade et al., 2011), the authors work around the issue
by presenting an algorithm that can efficiently per-
form region visibility computations on a large terrain
in external memory. Terrains that can fit in internal
memory remain desirable, however, as I/O operations
on external memory are algorithm bottlenecks.
Terrain simplification can be used to reduce the
terrain size and allow it to fit in internal memory.
See (Heckbert and Garland, 1997) for a survey of
simplification algorithms. For our irregular compar-
ison methods, we have used the quadric error-metric
based edge collapse scheme described in (Garland
and Heckbert, 1997) and (Garland, 1999), the greedy
cuts algorithm from (Silva et al., 1995) and (Silva and
Mitchell, 1998), and the greedy insertion algorithm
of (Garland and Heckbert, 1995). These methods are
described in greater detail Section 4.
Forward subdivision, which iteratively generates
fine resolution data from coarse resolution data, has
gained popularity as a geometric modeling technique.
Some well-known forward subdivision schemes in-
clude the corner-cutting algorithm from (Chaikin,
1974) and the interpolatory scheme of (Dyn et al.,
1987). In (Prusinkiewicz et al., 2003), the authors
describe two seperate but easily understood formal-
izations for forward subdivision: the standard matrix
notation and Lindenmayer system notation.
(Samavati and Bartels, 1999) use global least
squares data fitting to reverse forward subdivision
rules and obtain a curve that, after an application of
forward subdivision, yields an approximation of the
original curve. In (Bartels and Samavati, 2000), the
authors applied local least squares data fitting to gen-
erate local subdivision filters that can be used to ap-
ply reverse subdivision in linear time. Forward and
reverse subdivision form the core components of mul-
tiresolution decomposition and reconstruction, which
can be used to obtain a multiscale representation of
the terrain. See (Samavati et al., 2007) for further de-
tails on multiresolution and some of its applications.
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
144

Reverse subdivision has been used as a regularity-
preserving simplification scheme in (Losasso and
Hoppe, 2004). The authors make use of forward and
reverse Dyn-Levin subdivision to generate a viewer-
centered hierarchy of nested regular grids, called a
geometry clipmap, designed for use in terrain ren-
dering with level-of-detail control. The effect of re-
verse Dyn-Levin-Gregory subdivision and geometry
clipmaps on visibility test accuracy is presently un-
known. In this work, we examine the effect of reverse
subdivision upon visibility test accuracy.
The problem of applying terrain simplification to
optimize visibility computations has been studied pre-
viously in (Ben-Moshe et al., 2002). In their paper,
Ben-Moshe et al. present a measure of visibility sim-
ilarity between a terrain and its simplifications and
describe a novel method designed to maximize the
visibility similarity. Their algorithm first identifies a
network of features important to visibility (the “ridge
network”) and uses the points that constitute this net-
work to create an initial approximation of the terrain,
which is then refined by a greedy insertion algorithm.
However, their algorithm does not preserve regularity.
3 PROBLEM STATEMENT
Consider a terrain model T and a set of points P =
{p
1
, p
2
,..., p
n
} on T . For every T and P define a
visibility relation V
T,P
on P such that (p
i
, p
j
) ∈ V
T,P
if
the line segment (or visibility ray) between p
i
and p
j
does not intersect T . If (p
i
, p
j
) ∈ V
T,P
, we say that p
i
and p
j
are visible over T , otherwise we say they are
not visible over T . Assume there exists an algorithm
A that computes V
T,P
for any T and P.
We wish to find a terrain simplification function S
and a point relocation function R such that the compu-
tation of V
S(T ),R(P)
using algorithm A is faster and/or
requires less memory than the computation of V
T,P
using A, and such that |agree
+
| + |agree
−
| is maxi-
mized, where:
agree
+
= {(p
i
, p
j
) ∈ P × P|(p
i
, p
j
) ∈ V
T,P
and (R(p
i
),R(p
j
)) ∈ V
S(T ),R(P)
}
agree
−
= {(p
i
, p
j
) ∈ P × P|(p
i
, p
j
) 6∈ V
T,P
and (R(p
i
),R(p
j
)) 6∈ V
S(T ),R(P)
}
The visibility similarity between T and S(T ), or
percent accuracy of the visibility test after application
of the terrain simplification and point relocation, can
be calculated as:
|agree
+
| +|agree
−
|
|P ×P|
4 TERRAIN SIMPLIFICATION
Height maps are used extensively throughout the field
of GIS. The implicit connectivity of regular structures
allows the storage of terrain data in array-like data
structures, which are easily accessed and have low
memory usage beyond that needed for the raw data.
As technology advances and terrains can be
mapped at higher and higher resolutions, the memory
savings of height maps are particularly attractive. It is
often necessary to simplify such large data sets for
application use (Ben-Moshe et al., 2002), although
not all simplification algorithms preserve the desir-
able quality of regularity.
In this section we briefly describe the irregular
simplification methods we have used for comparison,
followed by a description of reverse subdivision and
the variants we have used for optimizing visibility
tests.
4.1 Quadric Error-based Collapse
(QEC)
Iterative vertex contraction, or edge collapsing, is a
mesh simplification paradigm in which edges deemed
to be unimportant via some importance metric have
their endpoints merged into a single point (Garland,
1999).
Edge collapse schemes differ from each other pri-
marily in the metrics used to select edges for contrac-
tion. For our comparisons we have used a shape pre-
serving edge collapse scheme based on Garland and
Heckbert’s quadric error metric (Garland and Heck-
bert, 1997) (Garland, 1999).
A set of planes is associated with each vertex of
the terrain model, obtained by extending the faces in-
cident to the vertex. For a given edge, the error result-
ing from collapsing the edge into a given point is com-
puted as the sum of the squared distances from the
collapse point to the planes associated with the edge’s
endpoints. The squared distance sum can be effi-
ciently computed using a structure called a “quadric”
(Garland, 1999).
4.2 Greedy Cuts Algorithm
The greedy cuts algorithm of Silva et al. (Silva
et al., 1995) (Silva and Mitchell, 1998) incremen-
tally removes regions (or, in Silva et al.’s terminology,
takes “bites”) of the yet-to-be-triangulated terrain us-
ing three basic operations: ear cutting, greedy biting,
and edge splitting. Each bite region is approximated
with a triangle, with some user-specified error toler-
ance ε.
REVERSE SUBDIVISION FOR OPTIMIZING VISIBILITY TESTS
145

4.3 Greedy Insertion Algorithm
Garland and Heckbert’s greedy insertion algorithm
(Garland and Heckbert, 1995) is a generalization
to 3D polygonal surfaces of the Douglas-Peucker
algorithm for approximating curves (Douglas and
Peucker, 1973). The algorithm starts with a coarse ap-
proximation of the terrain model. Iteratively, the mesh
vertex that is furthest from the approximation mesh is
added to the approximation. To ensure mesh quality,
a Delaunay triangulation on the mesh’s 2D projection
is maintained (Garland and Heckbert, 1995).
Of note is that the greedy insertion algorithm will
prioritize approximating high energy areas of the ter-
rain, as vertices in these areas will generally be fur-
thest from the approximation. Thus, low energy areas
of high energy terrains are approximated relatively
poorly.
4.4 Reverse Subdivision Methods
Subdivision is a family of methods for introducing
additional points into a curve or surface, with some
smoothness constraint. Reverse subdivision approx-
imates the inverse of this process; details necessary
for reconstruction are usually lost in a typical reverse
subdivision process. Both forward and reverse subdi-
vision can be applied iteratively to obtain the desired
number of curve/surface points.
In the case of curves, one starts with a vector of
points, c, that describe the curve. The goal of forward
subdivision is to use c (the “coarse points”) to gen-
erate a larger vector of points, f (the “fine points”),
that describes a curve with some known continuity.
These fine points are expressed as affine combinations
of the coarse points. Arranging the coefficients of the
affine combinations in a matrix, S, the application of
forward subdivision to c can be represented in matrix
notation as f = Sc. It is typical for such subdivision
matrices to be sparse and banded, with a repeating lo-
cal structure. This local pattern can be exploited to
apply subdivision in linear time (Prusinkiewicz et al.,
2003).
Curve-based subdivision schemes (both forward
and reverse) can be easily generalized to regular sur-
faces via the application of the curve scheme to the
surface’s rows and columns. Hence, we limit our
discussion of subdivision to curve schemes. Regular
surfaces after application of either forward or reverse
subdivision are guaranteed to remain regular.
Several subdivision schemes are derived from
knot insertion into a B-Spline curve (Samavati and
Bartels, 1999). Faber subdivision, for instance, is de-
rived from knot insertion into a second order B-Spline
curve. Given a curve defined by a discrete set of
points, the Faber scheme increases the resolution of
the curve by inserting midpoints (Samavati and Bar-
tels, 1999). Its subdivision matrix S has the form
S =











1 0 0 ··· 0
1
2
1
2
0 ··· 0
0 1 0 ··· 0
0
1
2
1
2
··· 0
0 0 1 ··· 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 0 ··· 1











Faber subdivision has the effect of introducing
more points into the curve/surface whilst not having
an effect on the shape. Intuitively we expect the re-
versal of this process to have a minimal effect on the
shape of the curve/surface and therefore the visibility
test results over the terrain.
There are several ways to reverse a subdivision
scheme. For our tests, we have used four variants of
reverse Faber subdivision.
4.4.1 Simple Reverse Faber
The first reverse Faber subdivision scheme we’ve ex-
amined is the simplest, and therefore we refer to it as
the “simple” reverse Faber scheme. Since Faber sub-
division introduces midpoints between vertices, the
simple scheme assumes every other curve point is a
midpoint and discards it. In other words, the sim-
ple reverse Faber scheme performs a downsampling
of the curve points by a factor of 2.
4.4.2 Global Least Squares (GLS) Reverse
Faber
To better approximate the original curve, the global
least squares (GLS) scheme adjusts the positions of
the vertices to minimize the least squares error, ||Sc −
f ||
2
, between the simplified and original curves. This
entails solving the overdetermined linear system Sc =
f for c.
Sc = f
S
T
Sc = S
T
f
c = (S
T
S)
−1
S
T
f
However, while the reverse subdivision matrix
(S
T
S)
−1
S
T
gives a valid result, since S is banded it
is often faster to solve for c directly from the linear
system Sc = f .
4.4.3 Local Least Squares (LLS) Reverse Faber
The third Faber scheme used for this work minimizes
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
146

the local least squares (LLS) error between the simpli-
fied and original curves (Bartels and Samavati, 2000).
The subdivision matrix S is different for different
lengths of the vectors c and f , despite the uniform
structure of the underlying subdivision scheme. Anal-
ysis of subdivision schemes independent of the size of
c and f is facilitated by the use of a local subdivision
matrix, L, which has the same structure as S but op-
erates on fixed-size c and f . R = (L
T
L)
−1
L
T
is the
local reverse subdivision matrix that minimizes the
l
2
-norm ||Lc − f ||
2
, where c = R f . Using the (pre-
computed) coefficients of R, the reverse subdivision
operation can be done efficiently in linear time.
Consider a vector, f , of 2n fine points (where n is
a positive integer). Let c
i
and f
j
(for i between 0 and
n−1, j between 0 and 2n −1) be the indexed points of
c and f , respectively. The vector c of n coarse points
resulting from local least squares on neighbourhoods
of five fine points is given by
c
0
= f
0
c
i
= −
1
6
f
2i−2
+
1
3
f
2i−1
+
2
3
f
2i
+
1
3
f
2i+1
−
1
6
f
2i+2
c
n−1
= f
2n−1
4.4.4 Feature Aware Reverse Faber
Our novel reverse subdivision algorithm attempts to
preserve terrain features using global least squares
error minimization. Based on the observation that
peaks and valleys in a terrain are important features
that affect visibility, our algorithm identifies the crit-
ical points that define these features and uses least
squares error minimization to preserve the spatial re-
lationships between them.
Identification of the “critical points” is closely re-
lated to the ridge network computation that lies at the
heart of the novel simplification algorithm in (Ben-
Moshe et al., 2002). For a curve, the critical points
are the endpoints and local maxima and minima. Let
p
i
∈ f denote the critical points. Then, the vectors
between the critical points (say v
i
= p
i
− p
i−1
), which
define the spatial relationships between them, are cal-
culated.
Figure 1: Identification of critical points and the vectors
between them.
To preserve these spatial relationships, we aug-
ment the linear system Sc = f with additional con-
straints. The vectors v
i
are appended to the end of
f and additional rows (one for each of the v
i
) are
appended to the matrix S. These rows have exactly
two non-zero entries, −1 and +1, for the points in
coarse space that correspond to the critical points used
to calculate the v
i
. That is, for v
i
= f
j
− f
k
, the
coarse point c
b j/2c
receives entry +1 in the matrix
row and coarse point c
bk/2c
receives entry −1, so that
v
i
≈ c
b j/2c
− c
bk/2c
.
For example, the linear system for the curve
shown in Figure 1 would be



















1 0 0 0 0
1
2
1
2
0 0 0
0 1 0 0 0
0
1
2
1
2
0 0
0 0 1 0 0
0 0
1
2
1
2
0
0 0 0 1 0
0 0 0
1
2
1
2
0 0 0 0 1
−1 1 0 0 0
0 −1 0 1 0
0 0 0 −1 1
























c
0
c
1
c
2
c
3
c
4





=



















f
0
f
1
f
2
f
3
f
4
f
5
f
6
f
7
f
8
v
0
v
1
v
2



















By solving the augmented linear system, a coarse
point vector c can be obtained that minimizes the er-
ror between the original and simplified curves and
preserves the spatial relationships between the criti-
cal points.
5 POINT RELOCATION
FUNCTIONS
When the terrain is simplified, the space the points
occupy is transformed. Hence, it is important to
consider how the points should be relocated into the
transformed space to best preserve the visibility re-
sults.
We have considered three point relocation func-
tions to transform the points from the original space
to the simplified space. These are described in the
following subsections.
5.1 Identity
The simplest relocation function is the identity func-
tion, which does not move the points. Supposing that
the simplified terrain is a good approximation of the
original (i.e. is shape-preserving) then it should be
unnecessary to move the points at all.
REVERSE SUBDIVISION FOR OPTIMIZING VISIBILITY TESTS
147

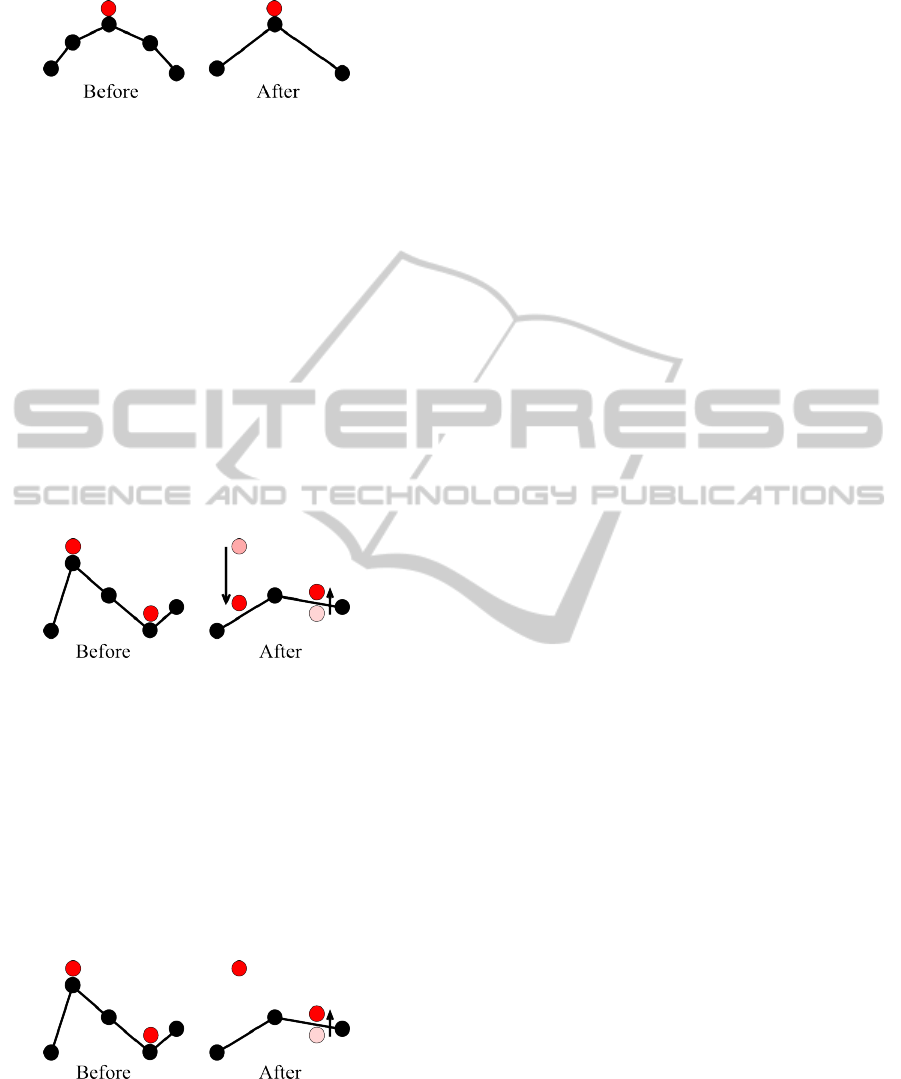
Figure 2: Illustration of the identity function.
5.2 Full Projection
Our second relocation function is the full projection
function. Given that the test points are situated atop
the original terrain, we suspect that reprojecting all
sample points vertically onto the simplified terrain
should produce similar visibility test results.
However, the full projection function suffers from
an important flaw. Consider a sharp terrain feature
simplified to a flat terrain feature, as in Figure 3. A
point situated atop the sharp feature would be able to
view terrain in lower regions. Once the point is pro-
jected onto the flat feature after simplification, how-
ever, its view of the lower regions will be occluded.
Hence, the visibility test accuracy may be diminished.
Figure 3: Illustration of the full projection function.
5.3 Half Projection
The half projection function is a hybrid between full
projection and identity that attempts to solve the prob-
lem of sharp features simplified to flat features oc-
cluding a point’s view. The function projects onto
the simplified terrain only those sample points that
lie within the half-space underneath the simplified ter-
rain, and leaves points above the terrain untouched.
Figure 4: Illustration of the half projection function.
6 COMPARISONS
In this section we describe and discuss our results
from comparing the visibility test accuracy of the var-
ious simplification schemes described throughout the
paper.
Visibility tests were conducted using a ray casting
approach on five different terrain models with varying
levels of sharp features, each tested using six random
distributions of fifty test points. The terrain models
(120×120 height maps) were each tested at three lev-
els of simplification: 25% of the original terrain size,
6% of the original terrain size, and 1.5% of the ter-
rain size (which correspond to the terrain size after 1,
2, and 3 iterative applications of reverse subdivision,
respectively).
6.1 Numerical Results
See Table 1 for the accuracy results after simplifica-
tion to 25% of the original terrain size, Table 2 for
the results after simplification to 6%, and Table 3 for
the results after simplification to 1.5%. For each sim-
plification method-relocation function pair, the aver-
age accuracy rate, µ, and its standard deviation, σ, are
given.
6.2 Discussion
Our results indicate that, while the reverse subdivision
methods have a more restrictive nature than the irreg-
ular simplification methods, the restriction to regular
surfaces does not significantly diminish the visibility
test accuracy. The reverse subdivision methods ap-
pear to be only marginally poorer at preserving visi-
bility test accuracy than the other methods, with fairly
similar standard deviations.
Of these, the simple reverse Faber scheme is un-
doubtedly the weakest. The other three variants (GLS,
LLS, Feature Aware) have approximately equal rates
of total accuracy, however, due to its superior run
time the LLS reverse Faber scheme emerges as the
preferred reverse subdivision scheme. Although our
novel algorithm did not show any improvement in av-
erage accuracy over the other subdivision methods, of
these three variants it tends to have the lowest devia-
tion.
While the half projection function shows promise
at low levels of simplification, as the degree of simpli-
fication increases its performance at preserving accu-
racy deteriotes quite substantially. The results for half
projection at 1.5% of the original terrain size were the
worst of the relocation functions.
Interestingly, the identity relocation function ap-
pears to have the most positive effect on visibility
test accuracy, having the highest average accuracies
and lowest deviations. We suspect this is because test
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
148

Table 1: Comparison results for 25% of original terrain size.
Simplification Accuracy Rates
Method Identity Full Projection Half Projection
QEC µ = 98.2%, σ = 1.2% µ = 97.2%, σ = 1.6% µ = 98.3%, σ = 0.9%
Greedy Cuts µ = 97.5%, σ = 1.5% µ = 96.7%, σ = 1.6% µ = 97.6%, σ = 1.2%
Greedy Insertion µ = 97.6%, σ = 1.6% µ = 97.0%, σ = 1.5% µ = 97.9%, σ = 1.2%
Simple Reverse Faber µ = 95.7%, σ = 1.7% µ = 94.4%, σ = 2.7% µ = 95.7%, σ = 2.2%
GLS Reverse Faber µ = 95.8%, σ = 2.2% µ = 94.5%, σ = 2.6% µ = 96.1%, σ = 2.0%
LLS Reverse Faber µ = 95.8%, σ = 2.2% µ = 94.5%, σ = 2.5% µ = 96.1%, σ = 2.0%
Feature Aware Reverse Faber µ = 95.7%, σ = 2.1% µ = 94.4%, σ = 2.4% µ = 95.9%, σ = 1.8%
Table 2: Comparison results for 6% of original terrain size.
Simplification Accuracy Rates
Method Identity Full Projection Half Projection
QEC µ = 94.1%, σ = 2.7% µ = 93.1%, σ = 3.0% µ = 94.0%, σ = 3.0%
Greedy Cuts µ = 87.4%, σ = 7.9% µ = 89.8%, σ = 4.7% µ = 89.9%, σ = 5.2%
Greedy Insertion µ = 91.2%, σ = 6.5% µ = 92.2%, σ = 2.9% µ = 93.6%, σ = 2.6%
Simple Reverse Faber µ = 91.1%, σ = 3.0% µ = 89.5%, σ = 4.7% µ = 89.7%, σ = 5.0%
GLS Reverse Faber µ = 92.7%, σ = 2.5% µ = 90.3%, σ = 4.4% µ = 91.5%, σ = 3.9%
LLS Reverse Faber µ = 92.7%, σ = 2.4% µ = 90.2%, σ = 4.5% µ = 91.5%, σ = 3.9%
Feature Aware Reverse Faber µ = 92.2%, σ = 2.6% µ = 90.1%, σ = 4.1% µ = 91.5%, σ = 3.5%
Table 3: Comparison results for 1.5% of original terrain size.
Simplification Accuracy Rates
Method Identity Full Projection Half Projection
QEC µ = 86.6%, σ = 4.8% µ = 86.5%, σ = 5.3% µ = 86.0%, σ = 6.3%
Greedy Cuts µ = 79.4%, σ = 8.7% µ = 79.0%, σ = 10.0% µ = 78.0%, σ = 12.1%
Greedy Insertion µ = 82.7%, σ = 7.9% µ = 81.6%, σ = 10.2% µ = 82.7%, σ = 13.1%
Simple Reverse Faber µ = 83.2%, σ = 4.7% µ = 82.2%, σ = 7.0% µ = 80.5%, σ = 8.1%
GLS Reverse Faber µ = 85.8%, σ = 3.9% µ = 83.7%, σ = 5.9% µ = 83.0%, σ = 7.0%
LLS Reverse Faber µ = 86.4%, σ = 3.5% µ = 84.0%, σ = 5.7% µ = 83.1%, σ = 7.0%
Feature Aware Reverse Faber µ = 86.6%, σ = 3.3% µ = 83.8%, σ = 5.5% µ = 83.5%, σ = 6.0%
Table 4: Comparison results for true positives/negatives at 1.5% of original terrain size.
Simplification Identity Accuracy Half Projection Accuracy
Method Visible Rays Not Visible Rays Visible Rays Not Visible Rays
QEC
µ = 90.0% µ = 79.8% µ = 96.8% µ = 77.1%
σ = 7.5% σ = 7.6% σ = 3.6% σ = 7.4%
Greedy Cuts
µ = 57.4% µ = 82.5% µ = 92.9% µ = 68.0%
σ = 22.4% σ = 7.9% σ = 6.0% σ = 11.5%
Greedy Insertion
µ = 58.6% µ = 89.8% µ = 85.1% µ = 80.9%
σ = 23.6% σ = 7.4% σ = 13.4% σ = 15.0%
Simple Reverse Faber
µ = 80.0% µ = 72.8% µ = 95.2% µ = 63.1%
σ = 13.2% σ = 22.0% σ = 4.6% σ = 23.3%
GLS Reverse Faber
µ = 80.8% µ = 78.4% µ = 93.9% µ = 70.0%
σ = 13.7% σ = 16.6% σ = 4.1% σ = 16.8%
LLS Reverse Faber
µ = 76.7% µ = 81.1% µ = 94.0% µ = 70.3%
σ = 16.6% σ = 15.3% σ = 4.6% σ = 16.3%
Feature Aware Reverse Faber
µ = 76.8% µ = 80.9% µ = 91.6% µ = 71.8%
σ = 16.6% σ = 16.4% σ = 5.9% σ = 16.0%
points which fall under the terrain after simplification
are not visible to most entities, and that projecting
these points onto the terrain where they may be visible
is detrimental to the overall accuracy. A comparison
of the rates of true positives and negatives between the
identity and half projection functions appears to sup-
port this assertion (see Table 4). We suspect that the
results would look different were the visibility tests
more localized.
REVERSE SUBDIVISION FOR OPTIMIZING VISIBILITY TESTS
149

7 CONCLUSIONS
After comparing several terrain simplification meth-
ods, we have identified local least squares Faber re-
verse subdivision as a fast regularity-preserving sim-
plification scheme that preserves visibility test accu-
racy well. Additionally, having tested various point
relocation functions, we have identified the identity
and full projection functions as good relocation func-
tion for preserving overall test accuracy. However,
more analysis is needed for the identity function us-
ing localized visibility tests.
ACKNOWLEDGEMENTS
The C implementation of Cl
´
audio Silva’s greedy cuts
algorithm, GcTin, was downloaded from his user page
at www.vistrails.org. The terrain models used for our
comparisons were obtained from the GcTin package.
Thanks go to C4i Consultants Inc. for motivating
the problem and assisting in research, and to Mitacs
Accelerate for sponsoring our collaboration.
Lastly, thanks go to NSERC for funds used to-
wards travel expenses.
REFERENCES
Andrade, M. V. A., Magalh
˜
aes, S. V. G., Magalh
˜
aes, M. A.,
Franklin, W. R., and Cutler, B. M. (2011). Efficient
viewshed computation on terrain in external memory.
Geoinformatica, 15(2):381–397.
Bartels, R. H. and Samavati, F. F. (2000). Reversing subdi-
vision rules: Local linear conditions and observations
on inner products. Journal of Computational and Ap-
plied Mathematics, 119(1-2):29–67.
Ben-Moshe, B., Mitchell, J. S. B., Katz, M. J., and Nir,
Y. (2002). Visibility preserving terrain simplification:
An experimental study. In Proceedings of SCG 2002.
Bresenham, J. E. (1965). Algorithm for computer control
of a digital plotter. IBM Systems Journal, 4(1):25–30.
Chaikin, G. M. (1974). An algorithm for high-speed curve
generation. Computer Graphics and Image Process-
ing, 3(4):346–349.
De Floriani, L. and Magillo, P. (1993). Algorithms for
visibility computation on digital terrain models. In
Proceedings of the 1993 ACM/SIGAPP Symposium on
Applied Computing: States of the Art and Practice,
SAC ’93. ACM, New York, NY, USA.
Douglas, D. H. and Peucker, T. K. (1973). Algorithms for
the reduction of the number of points required to rep-
resent a digitized line or its caricature. The Canadian
Cartographer, 10(2):112–122.
Duvenhage, B. (2009). Using an implicit min/max kd-tree
for doing efficient terrain line of sight calculations. In
Proceedings of AFRIGRAPH 2009.
Dyn, N., Levin, D., and Gregory, J. A. (1987). A 4-
point interpolatory subdivision scheme for curve de-
sign. Computer Aided Geometric Design, 4(4):257–
268.
Garland, M. (1999). Quadric-Based Polygonal Surface Ap-
proximation. PhD thesis, Carnegie Mellon University.
Garland, M. and Heckbert, P. S. (1995). Fast polygonal
approximation of terrains and height fields. Techni-
cal Report CMU-CS-95-181, Carnegie Mellon Uni-
versity.
Garland, M. and Heckbert, P. S. (1997). Surface simplifi-
cation using quadric error metrics. In Proceedings of
SIGGRAPH 1997.
Heckbert, P. S. and Garland, M. (1997). Survey of polygo-
nal surface simplification algorithms.
Losasso, F. and Hoppe, H. (2004). Geometry clipmaps:
Terrain rendering using nested regular grids. In ACM
SIGGRAPH 2004 Papers.
Prusinkiewicz, P., Samavati, F. F., Smith, C., and Kar-
wowski, R. (2003). L-system description of subdivi-
sion curves. International Journal of Shape Modeling,
9(1):41–59.
Samavati, F. F. and Bartels, R. H. (1999). Multiresolu-
tion curve and surface representation: Reversing sub-
division rules by least-squares data fitting. Computer
Graphics Forum, 18:97–120.
Samavati, F. F., Bartels, R. H., and Olsen, L. (2007). Lo-
cal b-spline multiresolution with examples in iris syn-
thesis and volumetric rendering. In Image Pattern
Recognition: Synthesis and Analysis in Biometrics,
volume 67 of Series in Machine Perception and Artifi-
cial Intelligence, pages 65–102. World Scientific Pub-
lishing.
Seixas, R. d. B., Mediano, M. R., and Gattass, M. (1999).
Efficient line-of-sight algorithms for real terrain data.
In Proceedings of SPOLM ’99.
Silva, C. T. and Mitchell, J. S. B. (1998). Greedy cuts:
An advancing front terrain triangulation algorithm. In
Proceedings of GIS 1998.
Silva, C. T., Mitchell, J. S. B., and Kaufman, A. E. (1995).
Automatic generation of triangular irregular networks
using greedy cuts. In Proceedings of the IEEE Con-
ference on Visualization 1995, pages 201–208, 453.
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
150