APPLICATION OF THE MP THEORY TO SYSTEMS BIOLOGY
Vincenzo Manca and Luca Marchetti
University of Verona, Department of Computer Science, Strada Le Grazie 15, 37134 Verona, Italy
Keywords:
Biomathematical discrete modelling, Systems biology, Metabolic P Systems.
Abstract:
The main framework analysis for the most part of biological dynamics remains the theory of ordinary differ-
ential equations (ODEs). However, ODEs present some intrinsic limitations in the evaluation of the kinetic
reaction rates. In contrast to ODEs, Metabolic P systems (MP systems), based on P˘aun’s P systems, were
introduced for modelling metabolic systems by means of suitable multiset rewriting grammars. In this work
three applications of MP systems are presented, for discovering the internal regulation logic of three phenom-
ena relevant in systems biology: i) the Goldbeter’s mitotic oscillator; ii) the glucose/insulin dynamics in the
Intravenous Glucose Tolerance Test; iii) the HER-2 oncogene-regulated transcriptome in human SUM-225
cells. Despite the differences between the considered phenomena, in all the cases a model was found that
exhibits good approximation of the observed time series and highlights results which are new or that have
been only theorized before.
1 INTRODUCTION
Systems biology (Ideker et al., 2001; Kitano, 2002)
has been brought to the forefront of life-science re-
search. Its goal is to understand biology at the sys-
tem level by examining the whole structure and the
dynamics of cellular and organismal function. How-
ever, the huge amount of experimental data which
very often can be measured by means of high through-
put technologies makes this job very difficult. For
overcoming the problem, mathematical modelling is
emerging as a suitable way for analysing data and de-
veloping new knowledge (Bailey, 1998). In partic-
ular, an important problem of systems biology is the
mathematical definition of dynamical systems that ex-
plain observed dynamics of phenomena under investi-
gation, by taking into account what is already known
about each phenomenon.
The main framework analysis for the most part
of biological dynamics remains the theory of ordi-
nary differential equations (ODEs). However, ODEs
present some intrinsic limitations in the evaluation
of the kinetic reaction rates. In fact, very often,
the evaluation of the kinetic reaction rates in dif-
ferential models is problematic because it may re-
quire measurements hardly accessible in living or-
ganisms. Moreover, these measurements dramati-
cally alter the context of the investigated processes.
In contrast to ODEs, Metabolic P systems (MP sys-
tems) (Manca et al., 2005; Manca, 2010), based
on P˘aun’s P systems (P˘aun, 2002), were introduced
for modelling metabolic systems by means of suit-
able multiset rewriting grammars (see (Decraene and
Hinze, 2010; Hinze et al., 2007) for other discrete ap-
proaches compared to ODE systems).
A Metabolic P system is essentially a multiset
grammar where multiset transformations are regu-
lated by functions (MP grammar). Namely, a rule
like a + b → c means that a number u of molecules
of kind a and u of kind b are replaced by u molecules
of type c. The value of u is the flux of the rule ap-
plication. Assume to consider a system at some time
steps i = 0, 1, 2, . . . , t, and consider a substance x that
is produced by rules r
1
, r
3
and is consumed by rule r
2
.
If u
1
[i], u
2
[i], u
3
[i] are the fluxes of the rules r
1
, r
2
, r
3
respectively, in the passage from step i to step i + 1,
i ∈ N, the set of natural numbers, then the variation of
substance x is given by:
x[i+ 1] − x[i] = u
1
[i] − u
2
[i] + u
3
[i].
In an MP system it is assumed that in any state
the flux u
j
of rule r
j
is provided by a state function
ϕ
j
, called regulator of the rule. A state is essen-
tially determined by the values of the system vari-
ables, that is, substances and parameters (quantities
which are not transformed by the rules). However,
usually only some variables enter as arguments of reg-
ulators, therefore if u
j
= ϕ
j
(x, y, . . .), the arguments
x, y, . . . of ϕ
j
will be called tuners of the regulator.
Substances, reactions, and regulators specify the fol-
303
Manca V. and Marchetti L..
APPLICATION OF THE MP THEORY TO SYSTEMS BIOLOGY.
DOI: 10.5220/0003852003030308
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2012), pages 303-308
ISBN: 978-989-8425-89-8
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

Table 1: Goldbeter’s oscillator, which has a cycle of about 25 min (Goldbeter, 1991).
dC
dt
= v
i
− v
d
X
C
K
d
+C
− k
d
C
dM
dt
= V
1
(1−M)
K
1
+(1−M)
−V
2
M
K
2
+M
dX
dt
= V
3
(1−X)
K
3
+(1−X)
−V
4
X
K
4
+X
V
1
=
C
K
c
+C
V
M1
, V
3
= MV
M3
lowing discrete dynamics (x[i]|i ∈ N) for any sub-
stance x, starting from the given value x[0], called
Equational Metabolic Algorithm (EMA):
x[i+ 1] = x[i] +
m
∑
j=1
α
j
u
j
[i] (1)
where m is the number of rules and α
j
are integer sto-
ichiometric coefficients determined by the reactions
acting on substance x. Moreover, a temporal interval
τ, a conventional mole size ν, and substances masses
are considered, which specify the time and population
(discrete) granularities respectively. In the following
the MP dynamics we will present are computed in
MATLAB by applying the EMA formula given in (1).
MP systems are equipped with a powerful re-
gression algorithm, called Log-Gain Stoichiomet-
ric Stepwise Regression (LGSS), which derives MP
models from the time series of observed dynam-
ics and that can be applied independently from any
knowledge about reaction rate kinetics (Manca and
Marchetti, 2011). LGSS represents the most recent
solution, in terms of MP systems, of the dynamical
inverse problem, that is, of the identification of (dis-
crete) mathematical models exhibiting an observed
dynamics and satisfying all the constraints required
by the specific knowledge about the modelled phe-
nomenon. The LGSS algorithm combines and ex-
tends the log-gain principles developed in the MP
system theory (Manca, 2008; Manca, 2009) with
the classical method of Stepwise Regression (Hock-
ing, 1976), which is a statistical regression technique
based on Least Squares Approximation and statistical
F-tests (Draper and Smith, 1981).
LGSS has been implemented by Luca Marchetti in
2010 as a set of MATLAB functions
1
. All the func-
tions have been ad hoc implemented (including the
stepwise regression function), and do not require ad-
ditional MATLAB toolboxes. The code which needs
harder computation (regression, simulation and tun-
ing of regression parameters) has been implemented
by taking advantage of the parallel processing fa-
1
See http://www.mathworks.it/index.html for details on
the MATLAB software.
cilities offered by the MATLAB Parallel Comput-
ing Toolbox (the software, however, runs also when
this toolbox is not installed). When the Optimiza-
tion Toolbox is installed in the system, LGSS supports
also the usage of the lsqlin function which computes
constrained linear least squares problems. This last
feature is very important when we need to force com-
plex constraints on the least squares estimation of the
computed regressor coefficients.
The size of the systems of equations solved by
LGSS depends on the number of substances and re-
actions of the MP system under examination and on
its temporal interval τ (a smaller temporal interval re-
quire longer time series and so larger system of equa-
tions). However, the regression usually ends in few
minutes (less than one minute in many cases, using a
common laptop with a dual core CPU and 4 Gbyte of
RAM memory), but it can increase to hours when the
system is very big (i.e. a system with many hundreds
of thousands of equations, and a regression dictionary
of hundreds of regressors).
Even if computational tools are available for eval-
uating unknown parameters of ODE models (Mai-
wald and Timmer, 2008; Hoops et al., 2006), LGSS
seems to point out a general methodology for solving
dynamical inverse problems. In fact, LGSS not only
discovers unknowns parameters, but suggests also the
form of regulators as a combination of basic func-
tions. This possibility could be very important in the
case where the knowledge about the phenomenon un-
der investigation is so poor that no clear idea is avail-
able about the kind of model underlying the observed
behaviour.
In the following, three applications of MP systems
will be presented for discovering, by means of LGSS,
the internal regulation logic of three phenomena rele-
vant in systems biology:
1. the Goldbeter’s mitotic oscillator (Goldbeter,
1991);
2. the glucose/insulin dynamics in the Intravenous
Glucose Tolerance Test (IVGTT);
3. the HER-2 oncogene-regulated transcriptome in
human SUM-225 cells (working in progress with
BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing
304

the Karmanos Cancer Institute, Wayne State Uni-
versity, Detroit).
Despite the differences between the considered phe-
nomena, in all the cases a model was found that ex-
hibits good approximation of the observed time series
and highlights results which are new or that have been
only theorized before (Manca and Marchetti, 2010a;
Manca et al., 2011; Marchetti and Manca, 2011).
2 MP GOLDBETER’S MITOTIC
OSCILLATOR
Rhythmic phenomena represent one of the most strik-
ing manifestations of dynamic behaviour in biological
systems. Understanding the molecular and cellular
mechanisms responsible for oscillations is crucial for
unravelling the dynamics of life (Goldbeter, 2002).
The Goldbeter’s mitotic oscillator represents the
simplest form of mitotic trigger mechanism found in
early amphibian embryos (Goldbeter,1991). The fun-
damental mechanism of mitotic oscillations concerns
the periodic change in the activation state of a pro-
tein produced by the cdc2 gene in fission yeast or by
homologous genes in other eukaryotes. The simplest
form of this mechanism is found in early amphibian
embryos. Here (see the picture in the left part of Ta-
ble 1) cyclin (C) is synthesized at a constant rate and
triggers the transformation of inactive (M
+
) into ac-
tive (M) cdc2 protein, which leads to the formation
of a complex known as M-phase promoting factor
(MPF). MPF triggers mitosis, but at the same time
M elicits the activation of a protease from state X
+
to
X. The active protease then degrades cyclin resulting
in the inactivation of cdc2. This brings the cell back
to initial conditions and a new division cycle can take
place. The ODE presented in Table 1 is the differ-
ential model of dynamics described in the right part
of Table 1, where C, M, X are the concentrations of
C, M, X respectively and 1− M, 1− X are the concen-
trations of M
+
, X
+
respectively (the definitions of the
parameters of the ODE model are not simple and are
not relevant for our further discussion, however they
can be found in (Goldbeter, 1991)).
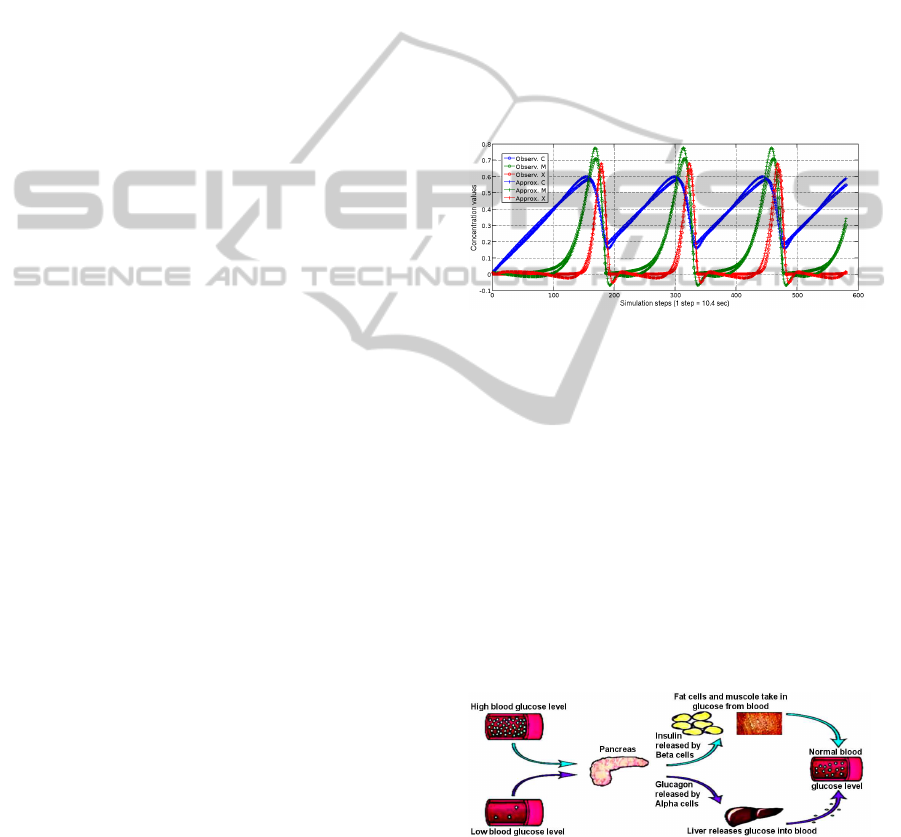
In (Manca and Marchetti, 2010a) LGSS has been
applied to Goldbeter’s oscillator for showing that MP
systems yield a robust method for biological mod-
elling. In this manner, were automatically generated
700 models of this oscillator, which, for the most part,
provide the same order of approximation of Gold-
beter’s model (see Table 2). Moreover, by consid-
ering the phenomenon at different values of τ, dif-
ferent models have been obtained and in many cases
the analytical form of these models is simpler than
Goldbeter’s model. These models have been also cat-
egorised with respect to the analytical form of their
regulators. In this way a set of grammatical schemata
was obtained which express the regulation relation-
ship acting on the systems in different intervals of the
temporal interval τ.
Table 2: Example of MP mitotic oscillator (τ = 10.4 sec).
Constants and initial values as in (Manca and Marchetti,
2010a).
r
1
:
/
0 → C ϕ
1
= v
i
r
2
:C →
/
0 ϕ
2
= k
1
+ k
2
M + k
3
X −k
4
CM
r
3
: M
+
→ M ϕ
3
= k
5
+ k
6
CM
r
4
: M → M
+
ϕ
4
= k
7
M + k
8
X
r
5
: X
+
→ X ϕ
5
= k
9
C+ k
10
M
r
6
: X → X
+
ϕ
6
= k
11
+ k
12
X +k
13
C
2
+ k
14
CM
3 GLUCOSE-INSULIN
INTERACTIONS IN THE IVGTT
The Intra Venous Glucose Tolerance Test (IVGTT) is
an experimental procedure used to study the glucose-
insulin endocrine regulatory system. Glucose is the
primary source of energy for body’s cells. It is trans-
ported from the intestines or liver to body cells via
the bloodstream, and is absorbed by the cells with
the intervention of the hormone insulin produced by
the pancreas. Normally, in mammals the blood glu-
cose concentration is tightly regulated as a part of
metabolic homeostasis (see Figure 1).
Figure 1: The glucose homeostasis.
If the plasma glucose concentration level is con-
stantly out of the usual range, then we are in presence
of blood glucose problems. In particular, when this
level is constantly higher than the range upper bound,
we are in presence of Diabetes: a dreadfully severe
and pervasive illness which concerns a good number
APPLICATION OF THE MP THEORY TO SYSTEMS BIOLOGY
305

of structures in the body. This motivates researches
to study the glucose-insulin endocrine regulatory sys-
tem.
The intravenous glucose tolerance test focuses on
the metabolism of glucose in a period of 3 hours start-
ing from the infusion of a bolus of glucose at time
t = 0. It is based on the assumption that, in a healthy
person, the glucose concentration decreases exponen-
tially with time followingthe loading dose. In (Manca
et al., 2011) Metabolic P systems theory has been ap-
plied for developing new physiologically based mod-
els of the glucose-insulin system which can be applied
to the IVGTT. In that work, ten data-sets obtained
from literature were considered and, for each of them,
an MP model which fits the data and explains the reg-
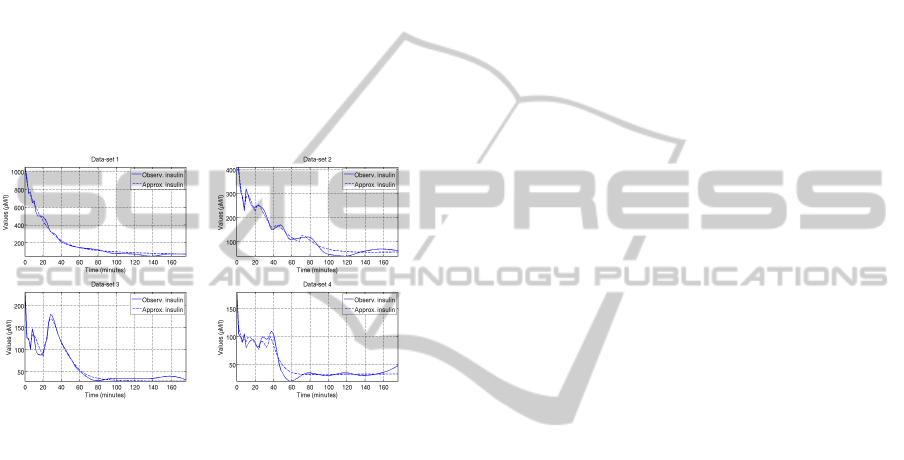
ulations of the dynamics was found (see Figure 2).
Figure 2: The calculated insulin dynamics related to four of
the considered data-sets (Manca et al., 2011) (τ = 2 min).
In the differential models proposed in literature,
the delay of the insulin release is approached by
adding artificial substances or by considering a delay
integral kernel. Here, instead, the problem has been
solved by assuming that the insulin production is reg-
ulated by the plasma glucose concentration level both
at the current time and at some previous simulation
steps (glucose memories as introduced in (Manca and
Marchetti, 2010b)). This has permitted to point out,
in a more natural and detailed way, the delays which
act in the insulin production. Moreover, even if dif-
ferences were found in the regulation governing the
release of insulin, it was possible to observe a com-
mon logic which before was only theorized during the
development of the differential models (see (Manca
et al., 2011) for details). These preliminary results
and analysis suggest that MP models seem to pro-
vide comprehensive tools for discovering personal-
ized glucose-insulin dynamics.
4 MP ANALYSIS OF THE HER-2
ONCOGENE-REGULATED
TRANSCRIPTOME IN HUMAN
SUM-225 CELLS
The identification of new gene networks are now
an important part of systems biology. In addition to
high-throughputexperimental methods, mathematical
and computational approaches are indispensable for
the analysis of gene networks. Given the large num-
ber of components of most networks of biological in-
terest, connected by positive and negative feedback
loops, an intuitive comprehension of the dynamics
of the system is often difficult, if not impossible to
obtain. Mathematical modelling supported by com-
puter tools can contribute to the analysis of a regu-
latory network by allowing the biologist to focus on
a restricted number of plausible hypotheses. Many
reviews of the modelling and simulation of gene net-
works have been published in recent years (e.g. (Cao
et al., 2010; Bolouri and Davidson, 2002; Gilman
and Arkin, 2002; Jong, 2002; Hasty et al., 2001;
Smolen et al., 2000)), presenting the wide variety
of formalisms that have been proposed in the liter-
ature, such as oriented graphs, Bayesian networks,
Boolean networks, differential equations, stochastic
master equations and stochastic P systems.
MP systems were initially introduced to model
metabolic processes, but they can be successfully
used in each context where we want to infer models of
a system from a given set of time series. In (Marchetti
and Manca, 2011) an application of the MP theory to
gene expression analysis was developed. In this case,
a standard way for translating MP grammars involv-
ing gene expressions into corresponding quantitative
gene networks was found (see Table 3).
The number of the raw microarray time series
which need to be processed for a generic experiment
on human cells is usually of the order of tens of thou-
sands. Generally, however, only a small part of them
are related to the phenomenon under examination.
For this reason, before to start with the modelling of
the MP model, raw data need to be preprocessed fol-
lowing a methodology which comprises normaliza-
tion, filtering and clustering. This methodology has
been developed during a work in progress where the
MP theory has been successfully applied for defining
the gene network underlying the regulations acting on
the HER-2 oncogene-regulated transcriptome in hu-
man SUM-225 cells in order to define new therapies
for the breast cancer.
HER-2 is an epidermal growth factor receptor
which have been implicated in radioresistance in
BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing
306

Table 3: An example of MP grammar related to a gene network (Marchetti and Manca, 2011).
MP grammar Quantitative gene network
r
1
: G1 →
/
0 ϕ
1
= k
1
· G1
r
2
:
/
0 → G2 ϕ
2
= k
2
· G3+ k
3
· G4
r
3
: G2 →
/
0 ϕ
3
= k
4
· G2
r
4
: G2 → G3 ϕ
4
= k
5
· G1
r
5
: G3 →
/
0 ϕ
5
= k
6
· G3
r
6
:
/
0 → G4 ϕ
6
= k
7
· G2
r
7
: G4 →
/
0 ϕ
7
= k
8
· G4
breast cancer and other malignancies (see Figure 3).
The analysis started by considering more than 24000
time series and finished by pointing out 1175 genes
which seem to be HER-2 oncogene-regulated. These
genes have been clustered following the ad hoc pro-
cedure defined in (Marchetti and Manca, 2011) and,
finally, the MP model and the corresponding gene net-
work have been provided, which seem to explain the
regulation of the phenomenon.
Figure 3: The action of the HER-2 growth factor on the cell
transcriptome.
5 CONCLUSIONS
In contrast to ODEs, Metabolic P systems (MP sys-
tems), based on P˘aun’s P systems, were introduced
for modelling metabolic systems by means of suitable
multiset rewriting grammars. In this work, three ap-
plications of MP systems for discovering the internal
regulation logic of three phenomena relevant in sys-
tems biology have been presented.
The last two modelled phenomena are currently
under development in order to extend the MP method-
ology in cases more complex (i.e. the insulin-glucose
dynamics where C-peptide time series are taken into
account) or other kind of gene expression analysis re-
lated to other pathological situations. In this perspec-
tive we intend to develop algorithmic and computa-
tional tools for making the MP modelling more ade-
quate and useful in biomedical applications.
REFERENCES
Bailey, J. (1998). Mathematical modeling and analysis in
biochemical engineering: past accomplishments and
future opportunities. Biotechnology Progress, 14:8–
20.
Bolouri, H. and Davidson, E. (2002). Modeling transcrip-
tional regulatory networks. BioEssays, 24(12):1118–
1129.
Cao, H., Romero-Campero, F., Heeb, S., C´amara, M., and
Krasnogor, N. (2010). Evolving cell models for sys-
tems and synthetic biology. Systems and Synthetic Bi-
ology, 4(1):55–84.
Decraene, J. and Hinze, T. (2010). A Multidisciplinary Sur-
vey of Computational Techniques for the Modelling,
Simulation and Analysis of Biochemical Networks.
Journal of Universal Computer Science, 16(9):1152–
1175.
Draper, N. and Smith, H. (1981). Applied Regression Anal-
ysis, 2nd Edition. John Wiley & Sons, New York.
Gilman, A. and Arkin, A. (2002). Genetic “code”: Rep-
resentations and dynamical models of genetic compo-
nents and networks. Annual Review of Genomics and
Human Genetics, 3:341–369.
Goldbeter, A. (1991). A minimal cascade model for the
mitotic oscillator involving cyclin and cdc2 kinase.
PNAS, 88(20):9107–9111.
Goldbeter, A. (2002). Computational approaches to cellular
rhythms. Nature, 420:238–245.
Hasty, J., McMillen, D., Isaacs, F., and Collins, J. (2001).
Computational studies of gene regulatory networks:
In numero molecular biology. Nature Review Genet-
ics, 2(4):268–279.
Hinze, T., Hayat, S., Lenser, T., Matsumaru, N., and Dit-
trich, P. (2007). Hill Kinetics Meets P Systems: A
Case Study on Gene Regulatory Networks as Comput-
ing Agents in silico and in vivo. In Eleftherakis, G.,
Kefalas, P., and Paun, G., editors, Proceedings of the
Eight Workshop on Membrane Computing (WMC8),
pages 363–381. SEERC Publishers.
Hocking, R. (1976). The Analysis and Selection of Vari-
ables in Linear Regression. Biometrics, 32.
APPLICATION OF THE MP THEORY TO SYSTEMS BIOLOGY
307

Hoops, S., Sahle, S., Gauges, R., Lee, C., and Pahle, J.
(2006). COPASI–a COmplex PAthway SImulator.
Bioinformatics, 22(24).
Ideker, T., Galitski, T., and Hood, L. (2001). A new ap-
proach to decoding life: Systems biology. Annual Re-
view of Genomics and Human Genetics, 2:343–372.
Jong, H. (2002). Modeling and simulation of genetic regu-
latory systems: A literature review. Journal of Com-
putational Biology, 9(1):69–105.
Kitano, H. (2002). Systems biology: A brief overview. Sci-
ence, 295(5560):1662–1664.
Maiwald, T. and Timmer, J. (2008). Dynamical model-
ing and multi-experiment fitting with PottersWheel.
Bioinformatics, 24(18):2037–2043.
Manca, V. (2008). The metabolic algorithm for P systems:
Principles and applications. Theoretical Computer
Science, 404:142–155.
Manca, V. (2009). Algorithmic Bioprocesses, chapter 28:
Log-Gain Principles for Metabolic P Systems, pages
585–605. Natural Computing. Springer-Verlag.
Manca, V. (2010). Metabolic P systems. Scholarpedia,
5(3):9273.
Manca, V., Bianco, L., and Fontana, F. (2005). Evolu-
tions and Oscillations of P systems: Theoretical Con-
siderations and Application to biological phenomena.
LNCS, (3365):63–84.
Manca, V. and Marchetti, L. (2010a). Goldbeter’s Mitotic
Oscillator Entirely Modeled by MP Systems. LNCS,
6501:273–284.
Manca, V. and Marchetti, L. (2010b). Metabolic approx-
imation of real periodical functions. The Journal of
Logic and Algebraic Programming, 79:363–373.
Manca, V. and Marchetti, L. (2011). Log-Gain Stoi-
chiometic Stepwise regression for MP systems. Inter-
national Journal of Foundations of Computer Science,
22(1):97–106.
Manca, V., Marchetti, L., and Pagliarini, R. (2011). MP
modelling of glucose-insulin interactions in the Intra-
venous Glucose Tolerance Test. International Journal
of Natural Computing Research, 2(3):13–24.
Marchetti, L. and Manca, V. (2011). A methodology based
on MP theory for gene expression analysis. LNCS. In
print.
P˘aun, G. (2002). Membrane Computing. An Introduction.
Springer.
Smolen, P., Baxter, D., and Byrne, J. (2000). Modeling tran-
scriptional control in gene networks: Methods, recent
results, and future directions. Bulletin of Mathemati-
cal Biology, 62(2):247–292.
BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing
308