A NEW REGION-BASED PDE FOR PERCEPTUAL IMAGE

RESTORATION

Baptiste Magnier, Philippe Montesinos and Daniel Diep

LGi2P de l’Ecole des Mines d’Al

es, Parc Scientiﬁque Georges Besse, 30035 N

ımes Cedex 1, France

Keywords:

Image Restoration, Rotating Filters, Edge Detection, Anisotropic Diffusion.

Abstract:

In this paper, we present a new image regularization method using a rotating smoothing ﬁlter. The novelty of

this approach resides in the mixing of ideas coming both from pixel classiﬁcation which determines roughly

if a pixel belongs to a homogenous region or an edge and an anisotropic perceptual edge detector which

computes two precise diffusion directions. These directions are used by an anisotropic diffusion scheme.

This anisotropic diffusion is accurately controlled near edges and corners, while isotropic diffusion is applied

to smooth homogeneous and highly noisy regions. Our results and a comparison with anisotropic diffusion

methods applied on a real image show that our model is able to efﬁciently regularize images and to control the

diffusion.

1 INTRODUCTION

Partial Differential Equations (PDE’s) are widely

used in image restoration (Perona and Malik, 1990)

(Alvarez et al., 1992) (Weickert, 1998) (Tschumperl

2006). Indeed, images are considered as evolving

functions of time and PDE’s enable to smooth the im-

age while preserving important structures or details

(Aubert and Kornprobst, 2006). Filtering techniques

like (Nagao and Matsuyama, 1979) (Tomasi and Man-

duchi, 1998) are not adapted to preserve small object

in presence of strong noise.

In (Perona and Malik, 1990) and (Black et al.,

1998), diffusion is isotropic on homogenous regions

but decreases and becomes anisotropic near bound-

aries. Diffusion control is done with ﬁnite differences

so that many contours of small objects or small struc-

tures are preserved. However, highly noisy images

may generate a lot of undesired artifacts.

Edge detection is often used to detect image

boundaries in order to control a diffusion process and

then to preserve contours present in the image in a

PDE scheme. The Mean Curvature motion method

(MCM) consists to diffuse only along the contour di-

rection (Catt

e et al., 1995), even in homogeneous re-

gions. In some diffusion approaches, Gaussian ﬁlter-

ing is used for gradient estimation, so the control of

the diffusion is more robust to noise (Alvarez et al.,

1992) (Weickert, 1998) (Tschumperl

e and Deriche,

2005) (Tschumperl

e, 2006). The intention is to rest-

rict the diffusion process only along the tangential di-

rection to the gradient near edges and to tune the dif-

fusion using the gradient magnitude. On regions con-

sidered as homogenous, the diffusion is isotropic, on

the contrary, at edge points, diffusion is anisotropic

and inhibited. Nevertheless, it remains difﬁcult to

distinguish between high noise and small objects

that need to be preserved from the diffusion pro-

cess. In (Tschumperl

e, 2006), the author takes the

curvatures of speciﬁc integral curves into account

in the restoration process. PDE’s based on tensor

(Weickert, 1998) (Tschumperl

e and Deriche, 2005)

(Tschumperl

e, 2006) are very efﬁcient on noise free-

images, but do not provide really homogeneous re-

gions when the noise is high, because the noise cre-

ates a ﬁber effect in the image. Indeed, these diffusion

methods are adapted for the preservation of thin struc-

tures in the image.

In this paper, we present a rotating ﬁlter (inspired

by (Montesinos and Magnier, 2010), (Magnier et al.,

2011c) and (Magnier et al., 2011b)) able to detect ho-

mogenous regions and edges regions, even in highly

noisy images. Then, we present an anisotropic edge

detector which deﬁnes two directions for pixels be-

longing to edges. Finally, we introduce a method

for anisotropic diffusion which controls accurately

the diffusion near edge and corner points and dif-

fuses isotropically inside noisy homogeneous regions.

In particular, our detector provides two different di-

rections on edge and corner points, these informa-

Magnier B., Montesinos P. and Diep D..

A NEW REGION-BASED PDE FOR PERCEPTUAL IMAGE RESTORATION.

DOI: 10.5220/0003853000560065

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 56-65

ISBN: 978-989-8565-03-7

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

tions enable an anisotropic diffusion in these direc-

tions contrary to (Alvarez et al., 1992) where only one

direction is considered. In (Magnier et al., 2011c), the

authors introduce a new diffusion method to remove

the textures. This approache diffuse in two differ-

ent directions of a contour for each pixel near edges.

However, they are not adapted for image restoration

because an efﬁcient way of controlling the diffusion

is missing. In this paper, we extend this method to

restoration. More precisely, the diffusion is controlled

both by the gradient value and two directions issued

from an anisotropic edge detector (Montesinos and

Magnier, 2010).

We ﬁrst present in section 2 our rotating smooth-

ing ﬁlter. A pixel classiﬁcation using a bank of ﬁl-

tered images is introduced in section 3. Thereafter,

we present a anisotropic edge detector based on half

smoothing kernels in section 4. Our anisotropic dif-

fusion scheme is introduced in section 5. Section

6 is devoted to experimental results and comparison

with other methods. Finally, section 7 concludes this

paper.

2 A ROTATING SMOOTHING

HALF FILTER

(a) Smoothing ﬁlter.

(b) Rotating

ﬁlters.

5 10 15 20 25 30

X axis

Y axis

ﬁlter.

Figure 1: A rotating smoothing half ﬁlter. For (c): µ = 10

and λ = 1.

In our method, for each pixel of the original image,

we use a rotating half smoothing ﬁlter (illustrated in

Fig. 1) in order to build a signal s which is a function

of a rotation angle θ and the underlying signal. As

shown in (Montesinos and Magnier, 2010), (Magnier

et al., 2011c) and (Magnier et al., 2011b), smoothing

with rotating ﬁlters means that the image is smoothed

with a bank of rotated anisotropic Gaussian half ker-

nels:

(µ,λ)

(x,y,θ) = C · I

∗ H (−y) ·e

−



2λ

2µ



(1)

where I

corresponds to a rotated image

of orienta-

tion θ, C is a normalization coefﬁcient, (x,y) are pixel

coordinates, and (µ, λ) the standard-deviations of the

Gaussian ﬁlter. As we need only the causal part of the

ﬁlter, we simply “cut” the smoothing kernel by the

middle, this operation corresponds to the Heaviside

function H and the implementation is quite straight-

forward.

Some examples of smoothed images using our

half kernels G

(µ,λ)

(x,y,θ) are available in Fig. 2 (b)

and (c).

3 PIXEL CLASSIFICATION

In the following the image is represented as a function

deﬁned as :

I(x,y) : R

→ R.

This case corresponds to grey level images.

3.1 Pixel Description

The application of the rotating ﬁlter at one point of an

image in a 360 scan, provides to each pixel a charac-

terizing signal. In the case of a gray level image, the

pixel signal is a single function s(θ) of the orientation

angle θ. Fig. 2(d) is an example of s-functions mea-

sured at 6 points located on a noisy image. Each plot

represents in polar coordinates the function s(θ) of a

particular point. From these pixel signals, we now

extract the descriptors that discriminate edges and re-

gions.

3.2 Flat Area Detection

The main idea for analyzing a 360 scan signal is to

detect signiﬁcant ﬂat areas, which correspond to ho-

mogeneous or noisy regions of the image. Fig. 3(a)

shows the pixel signal s(θ) extracted from a point be-

longing to a contour. After smoothing, the derivative

(θ) is calculated and represented on Fig. 3(b). From

(θ), ﬂat areas are detected as intervals (i.e. angu-

lar sectors) with a small derivative (close to zero), i.e.

sets of values exceeding a given threshold s

in am-

plitude. Let us note α the largest angular sector. We

consider that we detect a ﬂat area when 30 < α < 360

(degrees).

The noise removal method consists to diffuse

isotropically inside homogenous (point 3 of Fig. 2(a))

As explained in (Montesinos and Magnier, 2010), the

image is oriented instead of the ﬁlter because it increases

the algorithmic complexity and allows to use a recursive

Gaussian ﬁlter (Deriche, 1992).

A NEW REGION-BASED PDE FOR PERCEPTUAL IMAGE RESTORATION

(a) Points selection in green

on a noisy image 420×395.

(b) Smoothed image θ = 10

degrees.

(d) Polar representation of s(θ)

for each points of (a).

Figure 2: Points selection and associated signal, µ = 10, λ = 1 and ∆θ = 5 (degrees).

and noisy regions (points 1 and 2) i.e. α = 360 (de-

grees). In order to keep sharp contours, the aim of this

approach is to diffuse anisotropically at edge points

(like points 5 and 6) and corner points (like point 4) so

as to preserve borders between regions. Black regions

in Fig. 3(c) show regions of ﬂat areas have been de-

tected (30 < α < 360 in degrees) in the Fig. 2(a). So

this image will be smoothed anisotropically in black

regions of Fig. 3(c) and isotropically in white regions.

As shown in Fig. 3(c), ﬂat area detection can be seen

as a rough edge detection method. In (Magnier et al.,

2011c), the curvatures of the signal s(θ) deﬁne two

directions used in anisotropic diffusion. These di-

rections are not enough precise for image restoration.

Here, we use the directions for the diffusion computed

from a new anisotropic edge detector which deﬁnes

also two directions, but much more precise, resulting

in a more precise diffusion.

0 30 60 90 120 150 180 210 240 270 300 330 360

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.45

s(θ)

degrees

0 30 60 90 120 150 180 210 240 270 300 330 360

−0.1

−0.08

−0.06

−0.04

−0.02

0.02

0.04

0.06

0.08

0.1

(θ)

degrees

(a) Original signal s(θ). (b) First derivative of s(θ).

Figure 3: Flat area detections from s(θ). µ = 10, λ = 1 and

∆θ = 5 (degrees).

4 EDGE DETECTION USING

HALF SMOOTHING KERNELS

(a) (b)

Figure 4: (a) Full and (b) Half Anisotropic Gaussian kernels

at linear portions of contours and at corners.

As diagrammed in Fig. 4 (a), steerable (Freeman

and Adelson, 1991) (Jacob and Unser, 2004) or

anisotropic edge detector (Perona, 1992) perform well

to detect large linear structures. However, near cor-

ners, the gradient magnitude decreases as the edge

information under the scope of the ﬁlter decreases.

Consequently, the robustness to noise decreases.

A simple solution to bypass this effect is to con-

sider paths crossing each pixel in several directions.

The idea developed in (Montesinos and Magnier,

2010) is to “cut” the derivative (and smoothing) ker-

nel in two parts: a ﬁrst part along a ﬁrst direction and

a second part along a second direction (see Fig. 4 (b).

At each pixel of coordinates (x, y), a derivation ﬁl-

ter is applied to obtain a derivative information called

Q (x,y,θ):

Q (x,y,θ) = I

∗C

· H (−y) ·x · e

−



2λ

2µ



(2)

where C

represents a normalization coefﬁcient. As

diagrammed in Fig. 6, Q (x, y,θ) represents the slope

of a line issued from a pixel in the perpendicular di-

rection to this line (see Fig. 7(b) for several signals

Q (x,y,θ)) issued from several images derivatives (Fig

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

(a) Rotated

derivation

ﬁlter.

(b) Gradient image.

◦

(d) Image derivative at θ =

275

◦

Figure 5: Image in Fig. 2 (a) derivate using different orien-

tations with µ = 10 and λ = 1. Normalized images.

5). To obtain a gradient k∇Ik and its associated direc-

tion η on each pixel P, we ﬁrst compute global ex-

trema of the function Q (x,y,θ), with θ

and θ

(as

illustrated in Fig. 7 (c)). θ

and θ

deﬁne a curve

crossing the pixel (an incoming and outgoing direc-

tion). Two of these global extrema can then be com-

bined to maximize k∇Ik, i.e. :

= argmax

θ∈[0,360[

(Q (x,y,θ)), θ

= arg min

θ∈[0,360[

(Q (x,y,θ))

(3)

and k∇Ik = Q (x, y,θ

) −Q (x,y,θ

Once obtained k∇Ik, θ

and θ

, edges can easily

be extracted by computing local maxima of k∇Ik in

the direction of the angle (θ

+ θ

)/2 followed by an

hysteresis threshold (see (Montesinos and Magnier,

Figure 6: Estimation of the slope turning around a pixel.

The z axis represents the pixel intensity.

2010) for more details). In this paper, we are only

interested by the two directions (θ

,θ

) and the gradi-

ent magnitude used in our diffusion scheme in section

5.2.

Due to the lengths of the rotating ﬁlters, it enables

to keep a robustness agains noise and compute two

precise diffusion orientations in the directions of the

edges. In (Magnier et al., 2011a), the authors have

evaluated the edge detection used in this method as a

function of noise level.

(a) Points selection in

green on image in Fig.

1(d).

(b) Q (x,y,θ) for each points

of (a).

-0.04

-0.03

-0.02

-0.01

0.01

0.02

0.03

0.04

360

Discretized angle (degrees)

Quality function

180

270

Figure 7: Points selection and its associated Q (x,y,θ),

µ = 10, λ = 1 and ∆θ = 2

5 ANISOTROPIC DIFFUSION IN

TWO DIRECTIONS WITH PDE

In several diffusion scheme: (Alvarez et al., 1992)

(Weickert, 1998) (Tschumperl

e and Deriche, 2005)

(Tschumperl

e, 2006), only one direction is predomi-

nantly considered at edges, corner points are treated

like edge points, this direction is tangential to the

edge. Tensor diffusion schemes preserve edges

(Weickert, 1998) (Tschumperl

e and Deriche, 2005)

(Tschumperl

e, 2006) but in order to remove high

noise while preserving contours, the standard devia-

tion of the Gaussian σ must be large. However this so-

lution will blur edges and break corners. For minimiz-

ing these effects we are going to consider the two di-

rections (θ

,θ

) provided by eq. 3 of the anisotropic

edge detector only in areas where ﬂat areas have been

A NEW REGION-BASED PDE FOR PERCEPTUAL IMAGE RESTORATION

detected (Fig. 7(d)).

5.1 Diffusion Scheme in Two Directions

Unlike (Alvarez et al., 1992) (Weickert, 1998)

(Tschumperl

e and Deriche, 2005) (Tschumperl

2006), our control function does not depend only

on the image gradient but on a pre-established clas-

siﬁcation map of the initial image. As stated in

section 3, this classiﬁcation is a rough classiﬁca-

tion between region and edges. Consequently, a dif-

fusion scheme with only this new control function

moves corner points according to the curvature of iso-

intensity lines. As a consequence, this scheme be-

haves as the MCM scheme (Catt

e et al., 1995), for

example a square is transformed into a circle after

some iterations. For minimizing this effect, authors

of (Magnier et al., 2011c) consider the two directions

and ξ

provided by the curvature of the signal s(θ).

Their diffusion process can now be described by

the following PDE:

∂I

∂t

= F

)∆I

+ (1 − F

))

∂

∂ξ

(4)

where t is the diffusion time, I

is the original im-

age, I

is the diffused image at time t, (ξ

,ξ

) the two

directions of the diffusion and F

represents regions

where ﬂat areas are detected (section 3.2) :

• F

= 0 in contours regions

• F

= 1 in homogeneous regions.

However, this diffusion scheme generates a blur

effect at edges because that the two directions ξ

and ξ

of the curvature of s(θ) are not enough pre-

cise than the directions θ

and θ

computed from the

anisotropic edge detector described in section 4.

5.2 New Perceptual Diffusion Scheme

In (Alvarez et al., 1992), the aim is to restrict the

diffusion process only along the tangential direction

to the gradient and tuned by the gradient magnitude.

Here, we aim to diffuse only in the θ

and θ

direc-

tions in regions of pixels classiﬁed as edge points.

Firstly, we control the diffusion in function of the gra-

dient magnitude and secondly in function of the angle

between the two directions of the diffusion θ

and θ

Fig 8 (a) and (b) shows a diffused image without con-

trol function where edges are lost and blurred.

In order to control the diffusion in function of the

gradient magnitude, we use the following function u:

u(k∇Ik) = e

−



k∇Ik



, with k ∈ [0,1]. (5)

(a) Diffused image without

control function.

(b) Zoom in (a).

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0 20 40 60 80 100 120 140 160 180

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(d) Control function v.

Figure 8: Diffused image without any control function

where blurring effect is too important and the two functions

u and v.

Using the anisotropic perceptual edge detector, we

are able to control the diffusion in function of the an-

gle between θ

and θ

(see eq. 3) called β. Indeed, at

the level of one pixel, the more β is close to 0, the less

the diffusion is important. On the contrary, more β is

close to 180 (in degrees), more the smoothing is im-

portant. The angular control function v can be deﬁned

as follows:

v(β) = e

−



180−β

180·h



, (6)

with h ∈ [0,1] and β = θ

− θ

[180](in degrees).

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

The new diffusion process presented in Fig. 9 (a)

and (b) is described by the following PDE :

∂I

∂t

= F

)∆I

+(1− F

))·



u(k∇Ik) + v(β)



∂

∂θ

(7)

Contrary to (Alvarez et al., 1992), we do not want

to inhibit the diffusion at edges because the two direc-

tions of the diffusion θ

and θ

are sufﬁciently precise

to preserve contours. The values k = 0.5 and h = 0.8

enable to accurately control the diffusion along edges

and corners.

(Anisotropic diffusion)

Flat areas detected

Edge

Isotropic diffusion

(a) Schema of our diffusion.

Original image

Flat area

Computation of

Anisotropic diffusion

in function of

and

in two directions

( )

Isotropic

diffusion

detection

YES

(b) Organigramm of our method.

tions.

(d) Zoom in (c).

Figure 9: Different steps of our diffusion scheme. (c)

and (d) correspond to the image in 7 (a) diffused with our

method, the blurring effect is small at edges.

6 EXPERIMENTAL RESULTS

In this section, we present some quantitative and qual-

itative results. In order to carry out some qualitative

results, we have conducted a number of tests with real

images. We analyzed the effect of adding a uniform

white noise on the original image using the following

formula:

= (1 −L) · I

+ L · I

with L ∈ [0,1],

where I

is the original image, I

an image of random

uniform noise, I

the resulting noisy image and L the

level of noise.

In our test, we performed an anisotropic diffusion

and compared our results with several methods.

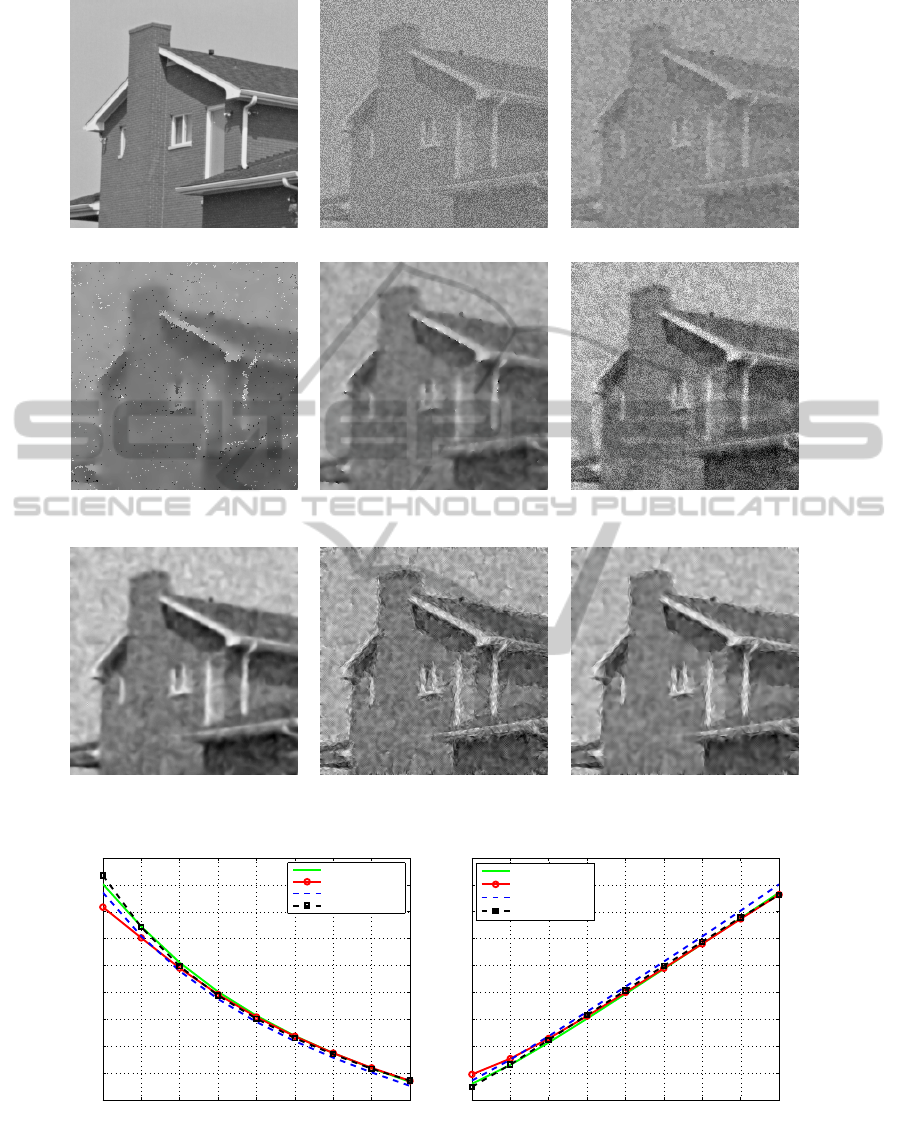
6.1 Qualitative Results

We have called our approach PR for Perceptual image

Restoration. In the images presented in Fig. 11 (b)

and 12 (b), the aim is to smooth the noise present in

the different images preserving all objects. We used

our scheme with µ = 5, λ = 1 and ∆θ = 5

◦

for ﬂat area

detection and the value of the threshold in amplitude

is equal to 0.05. Parameters used in anisotropic

edge detector in order to compute (θ

,θ

) are µ = 5,

λ = 1.5 and ∆θ = 2

◦

. The result of our anisotropic

diffusion is presented in the Fig. 11 (h), (i) and 12

(h), (i) after 5 or 10 iterations.

We compare our result with several approaches

as well as the well known Nagao (Nagao and Mat-

suyama, 1979) and bilateral ﬁlters (Tomasi and

Manduchi, 1998). We compare also with other

PDE’s approaches of Alvarez et al. (Alvarez et al.,

1992), Perona-Malik (Perona and Malik, 1990) and

Tschumperl

e (Tschumperl

e, 2006). For the bilateral

ﬁlter, Nagao ﬁlter and Perona-Malik method, results

are noisy in the different images (Fig. 11 and 12 (c),

(d), and (f)). The approaches of Alvarez et al. and

Tschumperl

e remove the noise but blur edges.

6.2 Inﬂuence of Noise

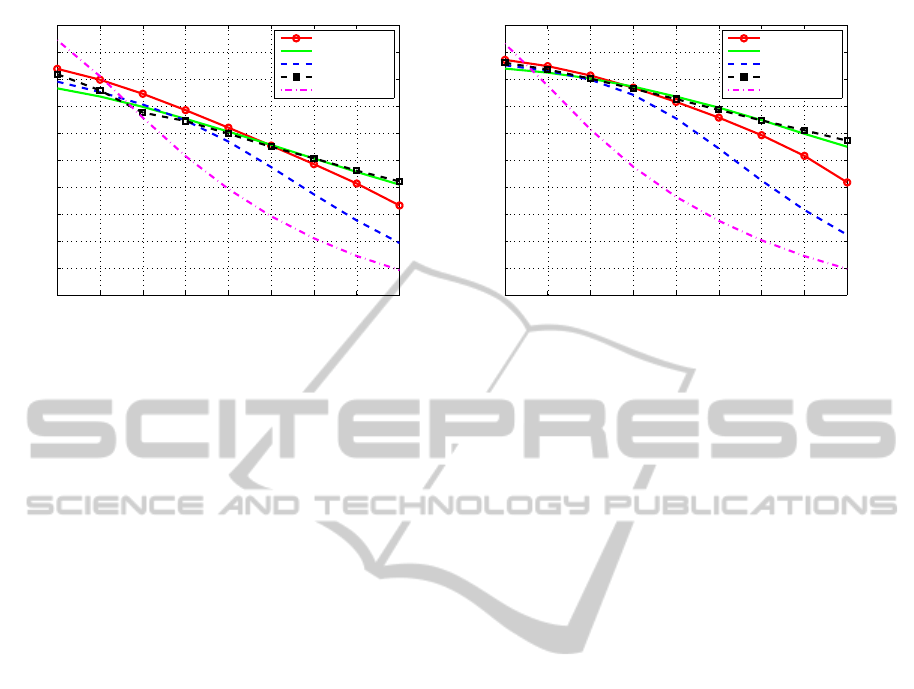
Curves have been plotted on Fig. 11 (j), (k) and 12

(j), (k), they present respectively the evolution of the

PSNR (Peak Signal to Noise Ratio) and RMSE. We

have compared our result after 5 and 10 iterations with

the bilateral ﬁlter, and the method of Tschumperl

The bilateral ﬁlter is used with two iterations and the

algorithm of Tschumperl

e with 20 iterations and a

standard deviation of the gaussian σ = 1 for each test.

For low levels of noise (L < 0.5), our approach and

this of Tschumperl

e perform well in terms of this two

measures. After 10 iterations our result seems better

A NEW REGION-BASED PDE FOR PERCEPTUAL IMAGE RESTORATION

10 20 30 40 50 60 70 80 90

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Noise level

SSIM

Man - SSIM

PR 5 iterations

PR 10 iterations

Bilateral filter

Tschumperlé

Noisy image

(a) Image in Fig. 11 (a).

10 20 30 40 50 60 70 80 90

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Noise level

SSIM

House - SSIM

PR 5 iterations

PR 10 iterations

Bilateral filter

Tschumperlé

Noisy image

(b) Image in Fig. 12 (a).

Figure 10: SSIM evolution in function of the noise level.

than 5 iterations when the noise is high. However,

PSNR and RMSE measures are not fully consistent

with human eye perception, that is why we have mea-

sured a similarity metric.

6.2.1 Perceptual Evolution

Instead of calculating a local difference like the PSNR

which does not take into account the perception of the

image, it exists a measure that estimates the similarity

between two images. This metric called SSIM (Struc-

tural SIMilarity) measures similar structures between

two images (Wang et al., 2004). It is based on several

windows of the image.

The measure will yield values between zero and

one, when the result is close to one, the structures are

considered as very well preserved. The total measure

of SSIM on the whole image is given by the average

SSIM on all windows.

Thus, we conducted SSIM measures plotted in

Fig. 10 in function of the level of noise on the two

images shown in Fig. 11 (a) and 12 (a). This measure

reﬂects better the preservation of the contours.

We observe, for our method, when the noise is less

than ﬁfty percent in the image, compared to 10 iter-

ations, 5 iterations keeps the shape better but when

it exceeds this threshold, 10 iterations are necessary.

The difference in the SSIM decreases between 5 and

10 iterations for noise less than ﬁfty percent when the

image is composed of ﬁne textures on the image of

the house in Fig. 12 (a). Our approach removes the

ﬁne textures and diffuse isotropically, resulting in a

loss of information compared to the original image.

Nevertheless, when the image is composed mainly

of small objects, the result of the SSIM seems better

for our approach with ﬁve iterations for the images

in Fig. 11 (a). On the contrary, an image composed

of large objects, like the house in Fig. 12 (a), SSIM

values crosses from a noise level of around forty per-

cent for 5 or 10 iterations. Beyond, 10 iterations are

necessary.

The bilateral ﬁlter gives good results when the

noise is small but the SSIM values decrease rapidly.

In general, Tschumperl

e’s scores are better than the

bilateral ﬁlter. However, our method with 10 itera-

tions gives the best results in terms of SSIM when the

noise level is between 30 and 70 percent (above 70

percent, the noise is too hard to compare such mea-

sures).

Fig. 13 shows a result of an ultrasound image of a

fetus composed of a high noise. After diffusion, edges

of the fetus are very sharped and the noise is totally

removed.

7 CONCLUSIONS

We have proposed in this paper a new method for dif-

fusing the noise in images by pixel classiﬁcation us-

ing a rotating smoothing ﬁlter followed by a PDE.

Our classiﬁcation method seems very promising as

we have been able to classify correctly homogenous

regions and edge regions for various image types. The

diffusion process that we have developed precisely

combines isotropic and anisotropic diffusion, and en-

ables to keep edges and corners of different objects

in highly noisy images. Comparing our results with

existing algorithms allows us to validate our method.

As introduced in Fig. 13, next on our agenda is to

enhance this method for medical images.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

(a) Original image 256×256. (b) Noisy image, L = 0.7. (c) Nagao ﬁlter.

(d) Perona-Malik, (e) Alevarez et al. (f) Bilateral ﬁlter

100 iterations. 20 iterations. 2 iterations.

(g) Tschumperl

e, (h) Our algorithm (i) Our algorithm

20 iterations, σ=1. 5 iterations. 10 iterations.

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

Noise level

PSNR

PR 5 iterations

PR 10 iterations

Bilateral filter

Tschumperlé σ = 1

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

Noise level

RMSE

PR 5 iterations

PR 10 iterations

Bilateral filter

Tschumperlé σ = 1

(j) PSNR evolution. (k) RMSE evolution.

Figure 11: Image restoration on an image containing small objects.

A NEW REGION-BASED PDE FOR PERCEPTUAL IMAGE RESTORATION

(a) Original image 256×256. (b) Noisy image, L = 0.7. (c) Nagao ﬁlter.

(d) Perona-Malik, (e) Alevarez et al. (f) Bilateral ﬁlter

100 iterations. 20 iterations. 2 iterations.

(g) Tschumperl

e, (h) Our algorithm (i) Our algorithm

20 iterations, σ=1 5 iterations. 10 iterations.

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

Noise level

PSNR

PR 5 iterations

PR 10 iterations

Bilateral filter

Tschumperlé σ = 1

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

Noise level

RMSE

BM 5 iterations

BM 10 iterations

Bilateral filter

Tschumperlé σ = 1

(j) PSNR evolution. (k) RMSE evolution.

Figure 12: Image restoration on an image containing large structures.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

(a) Original image 533×231.

(b) Restored image.

Figure 13: Ultrasound image.

REFERENCES

Alvarez, L., Lions, P.-L., and Morel, J.-M. (1992). Image

selective smoothing and edge detection by nonlinear

diffusion, ii. SIAM Journal of Numerical Analysis,

29(3):845–866.

Aubert, G. and Kornprobst, P. (2006). Mathematical prob-

lems in image processing: partial differential equa-

tions and the calculus of variations (second edition),

volume 147. Springer-Verlag.

Black, M., Sapiro, G., Marimont, D., and Heeger, D.

(1998). Robust anisotropic diffusion. IEEE Trans-

actions on Image Processing, 7(3):421–432.

Catt

e, F., Dibos, F., and Koepﬂer, G. (1995). A morpholog-

ical scheme for mean curvature motion and applica-

tions to anisotropic diffusion and motion of level sets.

SIAM J. Numer. Anal., 32:1895–1909.

Deriche, R. (1992). Recursively implementing the gaussian

and its derivatives. In International Conference On

Image Processing. A longer version is INRIA Research

Report RR-1893, pages 263–267.

Freeman, W. T. and Adelson, E. H. (1991). The design and

use of steerable ﬁlters. IEEE Transactions on Pattern

Analysis and Machine Intelligence, 13:891–906.

Jacob, M. and Unser, M. (2004). Design of steerable ﬁlters

for feature detection using canny-like criteria. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, 26(8):1007–1019.

Magnier, B., Montesinos, P., and Diep, D. (2011a). Fast

Anisotropic Edge Detection Using Gamma Correction

in Color Images. In IEEE 7th International Sympo-

sium on Image and Signal Processing and Analysis,

pages 212–217.

Magnier, B., Montesinos, P., and Diep, D. (2011b). Ridges

and valleys detection in images using difference of ro-

tating half smoothing ﬁlters. In Advances Concepts

for Intelligent Vision Systems, pages 261–272.

Magnier, B., Montesinos, P., and Diep, D. (2011c). Texture

Removal in Color Images by Anisotropic Diffusion.

In International Conference on Computer Vision The-

ory and Applications (VISAPP 2011), pages 40–50.

Montesinos, P. and Magnier, B. (2010). A New Perceptual

Edge Detector in Color Images. In Advances Concepts

for Intelligent Vision Systems, pages 209–220.

Nagao, M. and Matsuyama, T. (1979). Edge preserving

smoothing. CGIP, 9:394–407.

Perona, P. (1992). Steerable-scalable kernels for edge detec-

tion and junction analysis. IMAVIS, 10(10):663–672.

Perona, P. and Malik, J. (1990). Scale-space and edge

detection using anisotropic diffusion. IEEE Trans-

actions on Pattern Recognition and Machine Intelli-

gence, 12:629–639.

Tomasi, C. and Manduchi, R. (1998). Bilateral ﬁltering for

gray and color images. In International Conference

on Computer Vision, pages 839–846. IEEE.

Tschumperl

e, D. (2006). Fast anisotropic smoothing

of multi-valued images using curvature-preserving

PDE’s. International Journal of Computer Vision,

68(1):65–82.

Tschumperl

e, D. and Deriche, R. (2005). Vector-valued im-

age regularization with pdes: A common framework

for different applications. IEEE Transactions on Pat-

tern Analysis and Machine Intelligence, pages 506–

517.

Wang, Z., Bovik, A., Sheikh, H., and Simoncelli, E. (2004).

Image quality assessment: From error visibility to

structural similarity. Image Processing, IEEE Trans-

actions on, 13(4):600–612.

Weickert, J. (1998). Anisotropic diffusion in image process-

ing. Teubner-Verlag, Stuttgart, Germany.

A NEW REGION-BASED PDE FOR PERCEPTUAL IMAGE RESTORATION