ISSUES WITH PARTIALLY MATCHING FEATURE FUNCTIONS IN
CONDITIONAL EXPONENTIAL MODELS
Carsten Elfers, Hartmut Messerschmidt and Otthein Herzog
Center for Computing and Communication Technologies, University Bremen, Am Fallturm 1, 28357 Bremen, Germany
Keywords:
Approximate feature functions, Conditional random fields, Partially matching feature functions, Regulariza-
tion.
Abstract:
Conditional Exponential Models (CEM) are effectively used in several machine learning approaches, e.g., in
Conditional Random Fields. Their feature functions are typically either satisfied or not. This paper presents a
way to use partially matching feature functions which are satisfied to some degree and corresponding issues
while training. Using partially matching feature functions improves the inference accuracy in domains with
sparse reference data and avoids overfitting. Unfortunately, the typically used Maximum Likelihood training
includes some issues for using partially matching feature functions. In this context three problems (inequality
of influence, unlimited weight boundaries and local optima in parameter space) with Improved Iterative Scal-
ing (a popular training algorithm for Conditional Exponential Models) using such feature functions are stated
and solved.
1 INTRODUCTION
Conditional Exponential Models (CEM) are effec-
tively used in several machine learning approaches
(e.g., in the Maximum Entropy Markov Model
(MEMM) (McCallum et al., 2000) and in Conditional
Random Fields (CRF) (Lafferty et al., 2001)). CEMs
are using features (also called feature functions) to de-
scribe the data. Features describe arbitrary or multi-
ple aspects of an observation, like the feature good
weather which is satisfied if it is warm and sunny.
Machine learning methods using CEM are often as-
suming binary valued features, i.e., they are either sat-
isfied or not. However, in practice there are situations
in which no feature is satisfied but a prediction is still
desired. For the example the question may occur how
to decide if the weather is sunny but not warm without
a feature describing this observation? If warm means
more than 20 degrees of Celsius, what if it is only
19 degrees? The problem of missing features arises
typically in two situations: (1) When not enough fea-
tures have been specified in advance to represent the
data. (2) There is not enough reference data to train
the features, i.e., the influence of these features to
the inference is unknown (and therefore disregarded).
To overcome this problem we introduce the concept
of partially matching features, e.g., the feature good
weather may be satisfied by 50% when the weather is
sunny but it is not warm.
The problem of missing reference data has al-
ready been investigated for several learning ap-
proaches, e.g., in Input-Output Hidden Markov Mod-
els (Oblinger et al., 2005) and Markov Models (An-
derson et al., 2002). Encouraging experiments regard-
ing the problem of missing features have been made
for Conditional Random Fields in (Elfers et al., 2010).
In this paper we present the formal basis for CEM
with partially matching features (which is a necessary
step to overcome the problem of sparse reference data
and overfitting) and discuss several problems (and so-
lutions) regarding the training with Improved Iterative
Scaling (IIS) (Berger et al., 1996), the most applied
training algorithm to CEM.
The paper is organized as follows: In Sec. 2 we
introduce Conditional Exponential Models and define
partially matching feature functions. In Sec. 3 the
influence of partially matching feature functions to
the posterior distribution is investigated. In Sec. 4
the problems of Improved Iterative Scaling (IIS) with
partially matching feature functions are gathered and
solved by extending the algorithm. The paper finishes
with the conclusion and outlook in Sec. 5.
571
Elfers C., Messerschmidt H. and Herzog O..
ISSUES WITH PARTIALLY MATCHING FEATURE FUNCTIONS IN CONDITIONAL EXPONENTIAL MODELS.
DOI: 10.5220/0003855205710578
In Proceedings of the 4th International Conference on Agents and Artificial Intelligence (SSML-2012), pages 571-578
ISBN: 978-989-8425-95-9
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 CONDITIONAL EXPONENTIAL
MODELS AND PARTIALLY
MATCHING FEATURE
FUNCTIONS
Conditional Exponential Models are predominantly
used in the area of natural language processing (see
e.g., (Rosenfeld, 1996)). More recently they are also
successfully applied to other domains, e.g., to the do-
main of intrusion detection (Gupta et al., 2010). Us-
ing a CEM allows to relax the strong independence
assumptions typically made in the well-known Hid-
den Markov Model (HMM) (Rabiner, 1989). Con-
trary to a HMM the corresponding models using a
CEM (i.e., MEMM and CRF) allow multiple overlap-
ping and dependent features which are more appropri-
ate to describe a sequential context (i.e., concurrent,
previous and possibly next observations).
CEMs describe the data they are generated from
by the use of an exponential function. This function is
parameterized by a set of weighted feature functions,
each representing some aspect of the input data. The
weight of each feature function can be seen as a de-
gree of influence of the corresponding feature to the
posterior distribution.
Feature functions are typically binary real valued
as described in Def. 1 (cf. (Berger et al., 1996)).
Definition 1 (Feature Function). A feature function
f
0
(x, y) is a binary valued function dependent to a
discrete sequence of observations x = x
1
, ··· , x
t
and
a label y ∈ y from the set of all labels y:
f
0
(x, y) =



1 if the feature matches
on the given x and y
0 otherwise
(1)
Please note that sets of elements are indicated by
bold characters.
In this paper we are extending this to partially
matching feature functions as in Def. 2 to solve the
problem arising in the absence of matching feature
functions:
Definition 2 (Partially Matching Feature Function).
A partially matching feature function f (x, y) is a real
valued function in the interval [0, 1] dependent to a
discrete sequence of observations x = x
1
, ··· , x
t
and a
label y ∈ y from the set of all labels y. The value of
such a function is called degree of matching.
f (x, y) =



1 if the feature matches
]0, 1[∈ R if the feature matches partially
0 otherwise
(2)
A CEM belongs to the group of discriminative
models, which means that they only model the condi-
tional probability of labels y (or classes in the case of
classification) regarding a sequence of observations x.
The major difference to generative models (like e.g.,
Hidden Markov Models) is that they do not learn how
to generate samples or observations from the trained
model. Any assumptions about the underlying gener-
ative process do not need to be modeled.
In the following the notation of Conditional Ran-
dom Fields for CEM is used:
Definition 3 (Conditional Exponential Model).
CEMs are defined for a label y ∈ y (the set of labels)
conditioned under a vector of observations x regard-
ing a set of real valued weights λ and a corresponding
set of real valued feature functions f as:
p(y|x) =
1
Z(x)
exp
n
∑
i=1
λ
i
f
i
(x, y)
!
(3)
In a CEM a partition function (or normalization
function) Z is used to ensure that the result is a prob-
ability mass function.
Definition 4 (Partition Function). The partition func-
tion Z of a CEM is defined for an x over the sum of all
possible labels y as:
Z(x) =
∑
y∈y
exp
n
∑
i=1
λ
i
f
i
(x, y)
!
(4)
The objective during training this model is to find
an appropriate combination of weights λ to represent
the maximum likelihood solution with respect to the
given training data. This solution is typically found
by the Improved Iterative Scaling algorithm. How-
ever, in the application we found that this algorithm
has some problems by using real valued (or partially
matching) feature functions which is discussed in this
paper.
3 INFLUENCE OF PARTIALLY
MATCHING FEATURE
FUNCTIONS
In this section the bahavior of CEM with partially
matching feature functions is analyzed. In particular
how the degree of matching (cf. Def. 2) influences the
posterior distribution. Therefore, basic monotonic-
ity requirements are analyzed and proven. These are
necessary to preclude unexpected behavior of a CEM
using partially matching feature functions. Higher
matching feature functions should contribute more to
the posterior distribution than lower matching ones.
ICAART 2012 - International Conference on Agents and Artificial Intelligence
572

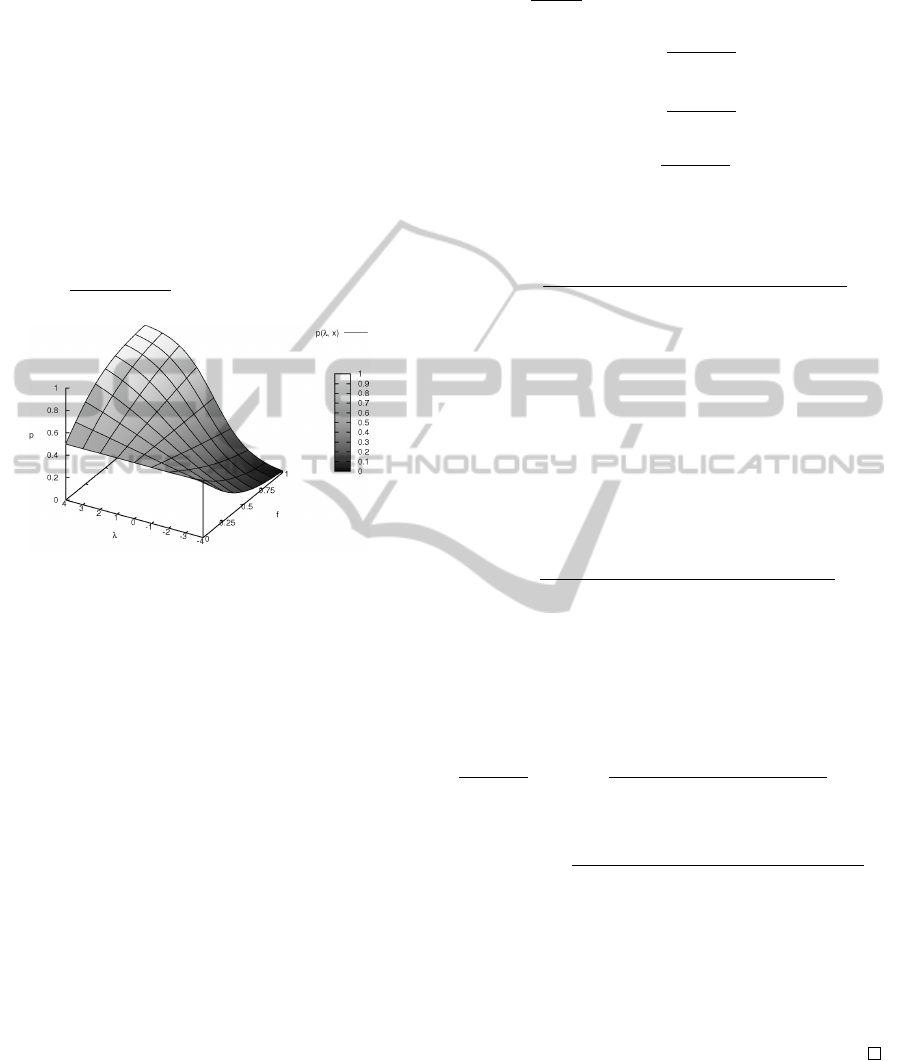
3.1 Monotonicity
The influence of the degree of matching f
i
on the pos-
terior distribution p(y|x) is highly dependent on the
assigned weight λ
i
to this feature function.
Example 1. In Fig. 1 this dependency is shown for
a given observation x, two labels y and two feature
functions. The feature function f
i
(x, ¯y) depends on
the corresponding weight λ
i
in the interval [−4, 4]
and only matches the plotted label ¯y, the other feature
function is unsatisfied (i.e., zero) and, therefore, is in-
dependent of the assigned weight. This setup leads
to the plotted equation for the posterior probability
p(λ, f ) =
exp(λ f )
exp(λ f )+exp(0)
with f = f
i
(x and ¯y).
Figure 1: The posterior probability with one partially
matching feature function and corresponding weights in the
interval [−4,4]
The a posteriori probability with weight 4 in-
creases for the feature function values more rapidly
and is more stable for higher degrees of match-
ing. Correspondingly the a posteriori probability de-
creases for negative weights.
This gives a first intuition how the exponential
model behaves with respect to the degree of matching
with arbitrary feature weights and partially matching
feature functions. Intuitively, the a posteriori proba-
bility increases with respect to the degree of match-
ing for positive weights and decreases for negative
weights. This is a fundamental requirement for us-
ing partially matching feature functions in CEM. In
the opposite case more exact matches of the feature
functions would lead to a greater deviation from the
Maximum Likelihood solution, which is obviously
undesirable. Therefore this monotonicity is one of the
most essential properties to show:
Theorem 1 (Value-monotonicity).
The a posteriori probability p behaves strictly mono-
tonic for non-zero weights (and is constant for zero
weights) with respect to the feature function value for
a given observation x and a fixed label ¯y. To specify
the monotonicity the first derivative of the posterior
probability p with respect to f
n
(x, ¯y) is used, and de-
noted as
∂p
∂ f
n
(x, ¯y)
:
∀λ
n
∈ λ > 0.
∂p
∂ f
n
(x, ¯y)
> 0. (5)
∀λ
n
∈ λ < 0.
∂p
∂ f
n
(x, ¯y)
< 0. (6)
λ
n
∈ λ = 0.
∂p
∂ f
n
(x, ¯y)
= 0. (7)
Proof. From Eqn. 3 and Eqn. 4:
p( ¯y|x) =
exp

n−1
∑
i=1
λ
i
f
i
(x, ¯y) + λ
n
f
n
(x, ¯y)

m
∑
j=1
exp

n−1
∑
i=1
λ
i
f
i
(x, y
j
) + λ
n
f
n
(x, y
j
)

(8)
We differentiate p( ¯y|x) with respect to a given ob-
servation x. Then the normalization function Z is
constant regarding f
n
except for f
n
(x, ¯y). C describes
these constant parts:
C :=
m
∑
y
j
6= ¯y, j=1
exp
n
∑
i=1
λ
i
f
i
(x, y
j
)
!
p =
exp

n−1
∑
i=1
λ
i
f
i
(x, ¯y) + λ
n
f
n
(x, ¯y)

C + exp

n−1
∑
i=1
λ
i
f
i
(x, ¯y) + λ
n
f
n
(x, ¯y)

The derivative of the numerator and the denom-
inator are both λ
n
exp

∑
n−1
i
λ
i
f
i
(x, ¯y) + λ
n
f
n
(x, ¯y)

.
Therefore the derivative of p
f
n
( ¯y|x) with respect to
f
n
(x, ¯y) is as follows:
∂p
∂ f
n
(x, ¯y)
=
λ
n
exp

n
∑
i=1
λ
i
f
i
(x, ¯y)

C

C+exp

n−1
∑
i=1
λ
i
f
i
(x, ¯y)+λ
n
f
n
(x, ¯y)

2
=
λ
n
exp

n
∑
i=1
λ
i
f
i
(x, ¯y)

m
∑
y
j
6= ¯y, j=1
exp

n
∑
i
λ
i
f
i
(x,y
j
)

!

m
∑
j=1
exp

n
∑
i=1
λ
i
f
i
(x,y
j
)

2
The denominator of the derivative is always posi-
tive and based on the fact that the exponential function
is always greater zero for real numbers the only way
to change the sign (or force the value to be zero) is the
parameter λ
n
. Therefore, Eqn. 5, Eqn. 6 and Eqn. 7
hold.
Similarly, a proof can be made for a corresponding
feature function weight:
ISSUES WITH PARTIALLY MATCHING FEATURE FUNCTIONS IN CONDITIONAL EXPONENTIAL MODELS
573

Theorem 2 (Weight-monotonicity). The a posteri-
ori probability behaves strictly monotonic for a given
observation and for non-zero feature function values
(and is constant for zero values) regarding the feature
function weight. The first derivation of the posterior
probability with respect to λ
n
is denoted as
∂p
∂λ
n
:
∀ f
n
(x, ¯y) > 0.
∂p
∂λ
n
> 0 (9)
∀ f
n
(x, ¯y) < 0.
∂p
∂λ
n
< 0 (10)
f
n
(x, ¯y) = 0.
∂p
∂λ
n
= 0 (11)
Proof. This proof can be done analogically to Proof
3.1 by differentiating p( ¯y|x) with respect to a given
observation. Then the normalization function Z is
constant with respect to λ
n
except for λ
n
occurring to-
gether with f
n
(x, ¯y). This leads to the following equa-
tion:
∂p
∂λ
n
=
f
n
(x, ¯y)exp

n
∑
i=1
λ
i
f
i
(x, ¯y)

m
∑
y
j
6= ¯y, j=1
exp

n
∑
i
λ
i
f
i
(x, y
j
)

!

m
∑
j=1
exp

n
∑
i=1
λ
i
f
i
(x, y
j
)

2
(12)
Theorem 1 and Theorem 2 show our presumption
that the higher the degree of matching and the abso-
lute value is, the higher is the influence on the a pos-
teriori distribution, respectively. This is essential for
working with partially matching feature functions and
degrees of matching.
3.2 Shape of Monotonicity
At first the shape of the monotonicity is investigated
by the analysis of the previously mentioned gradients.
Therefore Eqn. 12 is rearranged to get the dependen-
cies on the regarded variables λ
n
and f
n
.
∂p
∂λ
n
= f
n
(x, ¯y)exp
n−1
∑
i=1
λ
i
f
i
(x, ¯y)
!
exp(λ
n
f
n
(x, ¯y)) ·
m
∑
y
j
6= ¯y, j=1
exp

n−1
∑
i
λ
i
f
i
(x, y
j
)

exp(λ
n
f
n
(x, y
j
))
!
m
∑
j=1
exp

n−1
∑
i=1
λ
i
f
i
(x, y
j
)

exp(λ
n
f
n
(x, y
j
))
!
2
Now we assume that λ
n
and/or f
n
are 0 for a given
observation in all cases except ¯y: f
n
(x, y 6= ¯y) = 0. In
other words the feature function f
n
only matches the
label ¯y. With this assumption we can rewrite this
equation by introducing two constants C
1
and C
2
:
∂p
∂λ
n
=
f
n
(x, ¯y)C
1
exp(λ
n
f
n
(x, ¯y))C
2
(C
1
exp(λ
n
f
n
(x, ¯y)) +C
2
)
2
(13)
C
1
:= exp
n−1
∑
i=1
λ
i
f
i
(x, ¯y)
!
(14)
C
2
:=
m
∑
y
j
6= ¯y, j=1
exp
n−1
∑
i
λ
i
f
i
(x, y
j
)
!
exp(λ
n
f
n
(x, y
j
))
!
(15)
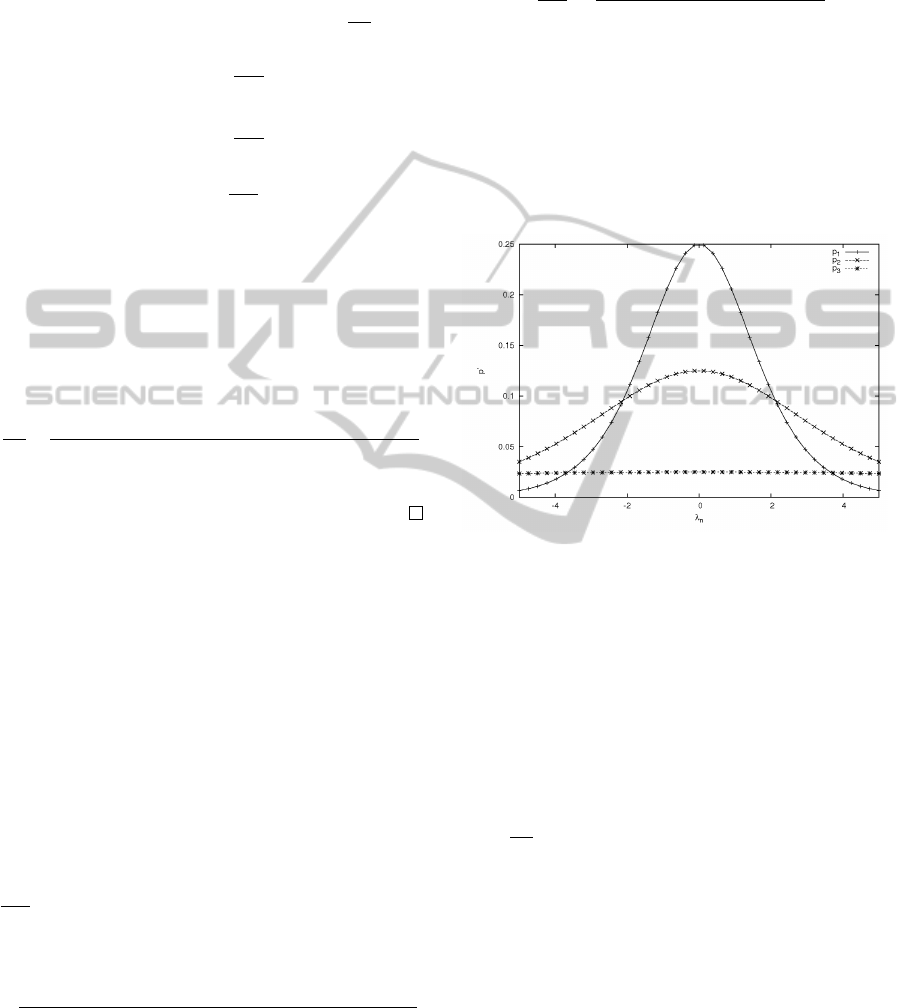
Figure 2: Plotted gradient p
0
for a feature function that is
satisfied by 1.0 (p
1
), by 0.5 (p
2
) and by 0.1 (p
3
) each with
C
1
= 0.1 and C
2
= 0.1.
The shape of the monotonicity is independent of
the amount of labels and feature functions (under the
mentioned assumptions) but depends on f
n
(x, ¯y) and
λ
n
as obvious from Eqn. 13. After this first conclu-
sion an example will demonstrate a problem regard-
ing the shape of monotonicity:
Example 2. In Fig. 2, three gradients p
1
, p
2
, p
3
of λ
n
occurring together with a certain f
n
(x, ¯y), i.e.
p
0
=
∂p
∂λ
n
are printed with C
1
= C
2
= 0.1 (i.e., the influ-
ence of a certain feature function value in dependency
of λ
n
). p
1
has the feature value f
n
(x, ¯y) = 1, p
2
has
f
n
(x, ¯y) = 0.5 and p
3
has f
n
(x, ¯y) = 0.1. The influence
of fully satisfied feature functions is converging faster
with respect to λ
n
than less satisfied feature functions.
The higher the weight the faster the experienced con-
vergence of the influence (the sharpener the graph).
This leads to the fact that if the assigned weight in-
creases over the intersection point with respect to an-
other feature function’s gradient, the feature function
with the most increasing influence changes. On the
one hand p
1
increases faster than p
2
and p
3
for λ = 0
and, on the other hand, p
1
increases slower than p
2
ICAART 2012 - International Conference on Agents and Artificial Intelligence
574

and p
3
for λ
n
= 4 which might be undesirable depend-
ing on the application domain or at least lead to coun-
terintuitive inference results. This also touches the
problem of overfitting since the influence decreases
very rapidly for increasing/decreasing λ
n
, e. g. if
a feature is satisfied by .1 the posterior probability
might increase from .0 to .8, by increasing the same
feature to .2 the posterior probability might increase
only by .1 to .9.
This leads to the first problem in using partially
matching feature functions with CEMs:
Problem 1 (Inequality of Influence). The increase
of influence of less satisfied feature functions may be
greater than more satisfied feature functions for some
assigned weights:
∂p
∂ f
n
(x, ¯y) = v
1
≥
∂p
∂ f
n
(x, ¯y) = v
2
, with
v
1
≤ v
2
for some unknown λ
n
.
(16)
At next we want to investigate ”the unknown λ”
stated in the problem. Therefore, the mentioned in-
tersection point in Example 2 can be determined by
the following equation for two feature function val-
ues f
n
= v
1
and f
n
= v
2
:
v
1
C
1
C
2
exp(λv
1
)
(C
1
exp(λv
1
) +C
2
)
2
=
v
2
C
1
C
2
exp(λv
2
)
(C
1
exp(λv
2
) +C
2
)
2
(17)
Theorem 3 (Monotonicity of the Increase of Influ-
ence).
The increase of influence of a feature function is al-
ways greater or equal than the influence of another
feature function with the same weight and a lower de-
gree of matching if −1 ≤ λ ≤ 1:
∂p
∂ f
n
(x, ¯y) = v
2
≥
∂p
∂ f
n
(x, ¯y) = v
1
, with
v
2
> v
1
if − 1 ≤ λ
n
≤ 1.
(18)
Proof. It is easy to see from Eqn. 13 that
∂p
∂ f
n
(x, ¯y)=v
2
≥
∂p
∂ f
n
(x, ¯y)=v
1
, with v
2
> v
1
holds for λ = 0. At next we
show with respect to λ the condition at which the fea-
ture function with the most influence may change.
Therefore, Eqn. 17 is rearranged to:
ln
v
1
exp(λv
1
)
(C
1
exp(λv
1
) +C
2
)
2
!
=
ln
v
2
exp(λv
2
)
(C
1
exp(λv
2
) +C
2
)
2
!
(19)
ln(v
1
) + λv
1
− 2 ln (C
1
exp(λv
1
) +C
2
) =
ln(v
2
) + λv
2
− 2 ln (C
1
exp(λv
2
) +C
2
)
The equation ln (x + y) = ln (x) + ln

1 +
y
x

is
used to rearrange to:
ln(v
1
) − λv
1
− 2 ln

1 +
C
2
C
1
exp(λv
1
)

=
ln(v
2
) − λv
2
− 2 ln

1 +
C
2
C
1
exp(λv
2
)

λ (v
2
− v
1
) = ln(v
2
) − ln (v
1
) +
2ln

1 +
C
2
C
1
exp(λv
1
)

− 2 ln

1 +
C
2
C
1
exp(λv
2
)

λ =
lnv
2
− ln v
1
v
2
− v
1
+
2
v
2
− v
1
ln
1 +
C
2
C
1
exp(λv
1
)
1 +
C
2
C
1
exp(λv
2
)
!
(20)
The term
2
v
2
−v
1
ln
1+
C
2
C
1
exp
(
λv
1
)
1+
C
2
C
1
exp
(
λv
2
)
!
from Eqn. 20 is al-
ways positive under the assumption v
2
> v
1
(from the
theorem) and λ ≥ 0.
1
Therefore this term is omitted
to find a lower bound λ for the intersection point:
λ ≤ ln

v
2
v
1

1
v
2
− v
1
(21)
λ(v
2
− v
1
) ≤ ln

v
2
v
1

(22)
At next the power series for the natural logarithm
is taken: ln
v
2
v
1
= 2
v
2
v
1
−1
v
2
v
1
+1
+R
1
(
v
2
v
1
), where R
1
(
v
2
v
1
) is pos-
itive if v
2
> v
1
which is assumed in the theorem. This
leads to the inequality:
2
v
2
− v
1
v
2
+ v
1
≤ ln

v
2
v
1

(23)
Due to the definition of the feature function
weights we can assume 0 ≤ v
2
+ v
1
≤ 2 which leads
to:
c(v
2
− v
1
) ≤ ln

v
2
v
1

(24)
with c =
2
v
1
+v
2
≥ 1. Compared to Eqn. 22 we have
proven that the inequality holds for λ ≥ 1. This proof
can be done correspondingly to a negative λ to find
the upper bound of λ which is λ ≤ −1. This inequal-
ity shows that the only possible intersection points of
λ (of the gradients) are outside (or exactly on the bor-
der) of the interval [−1, 1].
1
This equation is always negative under the assumption
λ < 0. This is helpful for the proof of the upper bound.
ISSUES WITH PARTIALLY MATCHING FEATURE FUNCTIONS IN CONDITIONAL EXPONENTIAL MODELS
575

Solution 1 (Inequality of Influence). Proof 3.2 shows
that Problem 1 can be easily solved by ensuring that
all weights are in the interval [−1, 1].
This solution is also applicable to a second prob-
lem regarding the training of a CEM with Improved
Iterative Scaling (IIS). The general absence of a limi-
tation of the weights’ interval during training with IIS
leads to a nearly unpredictable influence of partially
matching feature functions to the a posteriori proba-
bility (this has already been discussed in the sense of
regularization, e.g., in (Jin et al., 2003)).
Problem 2 (Unlimited Weight Boundaries). The in-
fluence of partially matching feature functions di-
rectly depends on the assigned weights. There exists
no boundary (neither an upper nor a lower boundary)
of the weights which makes the influence of partially
matching feature functions nearly unpredictable (e.g.,
due to possibly infinite weights).
Solution 2 (Unlimited Weight Boundaries). This
problem is already solved by Solution 1. However,
to solve this problem a less restrictive solution is pos-
sible: It is sufficient to ensure that all weights are in
a limited interval.
2
Additionally, the change of in-
fluence with respect to λ may also be regarded as a
feature to tune the model in the way how partially
matching feature functions should be integrated in the
inference process. As the weight interval increases,
the possible influence of partially matching feature
functions increases as well. This might be a reason
to choose a less restrictive interval than in Solution
1, however one must be aware of loosing the corre-
sponding properties from Theorem 3.
3.3 Exemplification
In the previous section we have proven the monotonic
properties of exponential models and their probability
space. In this section we investigate the behavior of
this model for multiple partially matching and com-
plementary feature functions by examples. Specifi-
cally the behavior of the model with weights over 1
are demonstrated.
Example 3. Fig. 3 shows a setup with two feature
functions ( f
1
= v
1
and f
2
= v
2
) matching on the first
of two possible labels (y = 1), i.e. they have a posi-
tive value and weight for this case. The second fea-
ture function’s weight has double the weight of the
2
This is easily possible while using Improved Iterative
Scaling due to the dependency on the update value to all the
model parameters. A combination with other regularization
methods such as fuzzy maximum entropy (cf. (Chen and
Rosenfeld, 2000)) may be desirable but is out of the scope
of this paper.
Figure 3: CEM with two feature functions ( f
1
= v
1
, f
2
= v
2
)
and two labels, λ
1
= 0.5, λ
2
= 1.
first one, i.e. λ
2
= 2λ
1
and λ
1
= 0.5. The feature
functions matching the second label (y = 2) are the
complement of the feature functions matching the first
label, i.e. f
1
(y = 1) = v
1
, f
1
(y = 2) = 1 − v
1
, f
2
(y =
2) = v
2
, f
2
(y = 2) = 1 − v
2
which can be regarded as
a typical example with respect to partially matching
feature functions.
We observe that this small model (with few fea-
ture functions) and limited weights (positive and less
than one) cannot represent all results in the proba-
bility space, e.g. if both feature functions are ful-
filled the posterior probability is not one as expected.
However, allowing negative weights or having more
matching feature functions overcomes this problem.
Please note the smooth distribution of the probabil-
ity space for such a small weight interval and that the
feature function value v
2
has a higher influence to the
posterior distribution than v
1
as expected.
Figure 4: CEM with two feature functions ( f
1
= v
1
, f
2
= v
2
)
and two labels, λ
1
= 5, λ
2
= 10.
Example 4. Fig. 4 shows the same setup as in Exam-
ple 3 but with ten times the weights, i.e. λ
1
= 5 and
λ
2
= 10.
It is obvious that this distribution is not as smooth
as the previous one. Specifically less matching fea-
ture functions have a higher influence to the poste-
rior distribution, e.g. v
1
= v
2
= 0.75 is nearly one.
The next thing to mention is the rapid decrease of the
ICAART 2012 - International Conference on Agents and Artificial Intelligence
576

influence for barely satisfied feature functions, e.g.
v
1
= v
2
= 0.25 is nearly zero. This gives an idea why
it might be preferable to lower the restriction regard-
ing the weights as stated in Solution 1 in special cases,
e.g. in a domain in which Problem 1 is of minor im-
portance and perhaps a stronger influence of partially
satisfied feature functions is desired.
4 ISSUES WITH IMPROVED
ITERATIVE SCALING
The Improved Iterative Scaling (IIS) algorithm
(Berger et al., 1996) uses a lower bound on the gra-
dient to optimize the weights of the Conditional Ex-
ponential Model regarding maximum likelihood (and
maximum entropy). The idea of this algorithm is that
each weight can be optimized (by gradient descent)
independently to the other weights in an iterative way.
Algorithm 1 shows the draft of this approach.
Algorithm 1 (Improved Iterative Scaling Algorithm).
• Start with λ
i
= 0
• Do for all λ
i
until convergence:
• Determine a weight update value δ
i
• Update λ
i
← λ
i
+ δ
i
The problem of this algorithm with partially
matching feature functions is that if the model is
trained for either satisfied or unsatisfied feature func-
tions, these values are optimized regarding maximum
likelihood (and maximum entropy) but the behavior
of partially matching feature functions during infer-
ence is not fully constrained by IIS. Bancarz et al.
(Bancarz and Osborne, 2002) found that there exists
a single global optimum in the likelihood space but
multiple local optima in the space of model parame-
ters. This leads to Problem 3:
Problem 3 (Local Optima in Parameter Space). Im-
proved Iterative Scaling converges the model parame-
ters to a single global optimum in the likelihood space
but to unspecified local optima in the space of model
parameters. This (also) leads to an unpredictable in-
fluence of the partially matching feature functions on
the a posteriori probability.
Bancarz et al. showed that the global maximum
can lead to different performances already for binary
valued feature functions. However, the problem has
a greater impact for partially matching feature func-
tions due to the unpredictable influence on the a pos-
teriori probability.
Example 5. Consider two feature functions with dif-
ferent weights, but both leading to a posterior prob-
ability of 100% for some label if they are fully satis-
fied. This is generally possible as stated in (Bancarz
and Osborne, 2002). If these feature functions are
both satisfied by only 50% this leads to a preference
to one label without any rational reason (because of
the multiple solutions for the model parameters).
Bancarz et al. suggested a simple solution to this
problem by initializing all weights with zero.
3
How-
ever, this is not enough due to the update at each it-
eration through IIS which results in a faster update of
some weights (and therefore to an unjustified diver-
gence of the model paramerters). This problem can
be seen in the gradient used in the IIS algorithm from
(Berger, 1997):
∂B(Λ)
∂δ
i
=
∑
x,y
˜p(x, y) f
i
(x, y) −
∑
x
˜p(x)
∑
y
p
Λ
(y|x)
∑
i
f
i
(x, y)exp

δ
i
f
#
(x, y)

The value of the trained model, denoted as
p
Λ
(y|x), is used in the gradient to determine the
weight updates and the updated weights itself are used
to determine the value of the model p
Λ
(y|x) as shown
in Algorithm 1.
4
Therefore, we need an additional
constraint to ensure that the model parameters are
also equal if the expected value of the feature func-
tions ˜p( f ) =
∑
x,y
˜p(x, y) f (x, y) are equal. This con-
straint must be independent of the iteratively chosen
model parameters:
∀i.∀ j. ( ˜p( f
i
) = ˜p( f
j
)) ⇒ (λ
i
= λ
j
) (25)
Solution 3 (Local Optima in Parameter Space). Prob-
lem 3 can be easily avoided by splitting the loop into
an update determination step for all weights and a
separate update step (as seen in Algorithm 2). This
leads to an equal treatment of the partially match-
ing feature functions and satisfies the additional con-
straint Eqn. 25.
The application of all solutions results in the fol-
lowing algorithm:
Algorithm 2 (Additionally Constrained Improved It-
erative Scaling Algorithm (AC-IIS)).
(1) Start with λ
i
= 0
Do until convergence:
Do for all λ
i
:
(2) Determine a weight update value δ
i
3
This has already been suggested in (Berger et al.,
1996), however in (Pietra et al., 1997; Berger, 1997) any
initial value for the weights have been allowed.
4
In this equation the notion of (Berger et al., 1996) has
been kept. f
#
(x, y) =
∑
i
f
i
(x, y).
ISSUES WITH PARTIALLY MATCHING FEATURE FUNCTIONS IN CONDITIONAL EXPONENTIAL MODELS
577

Do for all λ
i
:
(3) Update λ
i
← λ
i
+ δ
i
(4) Ensure that λ
i
is in a given weight
interval
Step (1) and the splitting of the convergence loop
into (2) and (3) solves Problem 3, step (4) solves
Problem 1 and Problem 2.
5 CONCLUSIONS AND
OUTLOOK
In this paper the Conditional Exponential Model
(which is used in Maximum Entropy Markov Models
and Conditional Random Fields) has been extended
to be used with partially matching feature functions.
This work enables the use of partially matching fea-
ture functions with Conditional Exponential Models
and Improved Iterative Scaling in a well-defined way
to overcome the problem of missing features. It has
been shown that the influence of partially matching
feature functions on the posterior probability changes
in the correct direction (i.e., monotonicity). Further
the impact of the weights has been analyzed. Prob-
lems regarding IIS have been identified and a solution
in a modified algorithm has been developed. Addi-
tionally the problem of overfitting is addressed by al-
lowing potentially all feature functions to be satisfied
to some degree of matching (and therefore smooth the
posterior distribution). In future work we are going to
show how partially matching feature functions may
be defined in a semantically intuitive way and present
empirical results of such a combined method. First
steps have already been done in the domain of intru-
sion detection.
ACKNOWLEDGEMENTS
This work was supported by the German Federal Min-
istry of Education and Research (BMBF) under the
grant 01IS08022A.
REFERENCES
Anderson, C. R., Domingos, P., and Weld, D. S. (2002). Re-
lational Markov models and their application to adap-
tive web navigation. In Proceedings of the eighth
ACM SIGKDD International Conference on Knowl-
edge Discovery and Data Mining, KDD ’02, pages
143–152, New York, NY, USA. ACM.
Bancarz, I. and Osborne, M. (2002). Improved itera-
tive scaling can yield multiple globally optimal mod-
els with radically differing performance levels. In
Proceedings of the 19th International Conference
on Computational Linguistics, volume 1, pages 1–7,
Morristown, NJ, USA. Association for Computational
Linguistics.
Berger, A. (1997). The improved iterative scaling algo-
rithm: A gentle introduction.
Berger, A. L., Pietra, V. J. D., and Pietra, S. A. D. (1996). A
maximum entropy approach to natural language pro-
cessing. In Computational Linguistics, volume 22,
pages 39–71, Cambridge, MA, USA. MIT Press.
Chen, S. and Rosenfeld, R. (2000). A survey of smooth-
ing techniques for ME models. In Speech and Audio
Processing, IEEE Transactions on, volume 8, pages
37 –50.
Elfers, C., Horstmann, M., Sohr, K., and Herzog, O. (2010).
Typed linear chain conditional random fields and their
application to intrusion detection. In Proceedings of
the 11th International Conference on Intelligent Data
Engineering and Automated Learning, Lecture Notes
in Computer Science. Springer Verlag Berlin.
Gupta, K. K., Nath, B., and Ramamohanarao, K. (2010).
Layered approach using conditional random fields for
intrusion detection. In IEEE Transactions on Depend-
able and Secure Computing.
Jin, R., Yan, R., Zhang, J., and Hauptmann, A. G. (2003).
A faster iterative scaling algorithm for conditional ex-
ponential model. In Proceedings of the 20th Interna-
tional Conference on Machine Learning, pages 282–
289.
Lafferty, J. D., McCallum, A., and Pereira, F. C. N. (2001).
Conditional random fields: Probabilistic models for
segmenting and labeling sequence data. In Proceed-
ings of the Eighteenth International Conference on
Machine Learning, ICML ’01, pages 282–289, San
Francisco, CA, USA. Morgan Kaufmann Publishers
Inc.
McCallum, A., Freitag, D., and Pereira, F. C. N. (2000).
Maximum entropy markov models for information ex-
traction and segmentation. In Proceedings of the Sev-
enteenth International Conference on Machine Learn-
ing, ICML ’00, pages 591–598, San Francisco, CA,
USA. Morgan Kaufmann Publishers Inc.
Oblinger, D., Castelli, V., Lau, T., and Bergman, L. D.
(2005). Similarity-based alignment and generaliza-
tion. In Proceedings of ECML 2005.
Pietra, S. D., Pietra, V. D., and Lafferty, J. (1997). In-
ducing features of random fields. In IEEE Transac-
tions on Pattern Analysis and Machine Intelligence,
volume 19, pages 380 –393.
Rabiner, L. R. (1989). A tutorial on hidden markov mod-
els and selected applications in speech recognition. In
Proceedings of the IEEE, volume 77, pages 257–286.
Rosenfeld, R. (1996). A maximum entropy approach to
adaptive statistical language modeling. In Computer,
Speech and Language, volume 10, pages 187–228.
ICAART 2012 - International Conference on Agents and Artificial Intelligence
578