A GENERAL MOTION REPRESENTATION

Exploring the Intrinsic Viewpoint of a Motion

Gutemberg Guerra-Filho

Department of Computer Science and Engineering, University of Texas at Arlington,

500 UTA Blvd, Arlington, TX, U.S.A.

Keywords: Motion Capture Format, Motion Representation, Pre-rotation Transformation.

Abstract: We propose a novel motion representation, named General Motion Representation (GMR), which explicitly

contains the absolute world coordinates of the meaningful joints, while still specifying every other joint with

rotational data relative to their respective parent joints. More specifically, our representation supports

multiple roots where any joint can be a root due to the use of a novel pre-rotation format for the construction

of local transformation matrices. Hence, our general motion representation allows for all intermediate data

structures between fully rotational and fully translational data. The use of multiple roots also implies the

representation of partial motion considering a subset of joints. We introduce the general motion

representation to consider multiple roots with the support of three operations (shift root, split skeleton tree,

and join skeleton trees). These operations allow reduced skeletal complexity because of the application of

pre-rotation local transformation matrices which eliminates the requirement for dummy joints. We also

present procedures to convert from raw marker data or post-rotation formats. We demonstrate the highly

efficient computation of per-frame joint positions and orientations. Our experimental results show that

GMR outperforms traditional motion formats in both speed and flexibility. At the full translational

configuration, GMR is around seven times faster than bvh.

1 INTRODUCTION

A fundamental issue for problems involving the

synthesis and analysis of human movement is the

representation for three-dimensional human motion.

With regards to human motion representation,

motion capture records the skeletal motion of a

human body by reconstructing the evolution of the

angles of articulated joints in a skeleton model.

In this paper, we address the problem of finding

a skeletal motion representation that allows the

explicit description of only the essential joints for a

particular motion in terms of world coordinates

while the non-essential joints are described by

rotational data inferred according to a skeleton

model. Formally, given a set M of three-dimensional

points representing the Cartesian location of markers

placed on the skin of the human subject at each time

frame during motion capture; a skeleton model S(G,

R) that consists of an adjacency graph G (where

nodes represent articulated body parts and edges

represent joints connecting these body parts) and a

relation R between markers and body parts stating

which markers belong to each body part; and a set E

of essential joints; we want to find a motion

representation such that essential joints are described

by 3D Cartesian points and non-essential joints are

described by rotational angles. Our main objective is

to find algorithms to construct this generalized

motion representation in order to consider any

possible set of essential joints. The motion

representation is obtained either from marker data

(as stated above) or from other existing

representations (e.g., single-root motion capture

data). A secondary objective is to develop the

necessary operations to allow the transformation of

the motion representation from any current set of

essential joints E

to any other target set of essential

joints E

We propose a novel motion representation,

named General Motion Representation (GMR),

which supports all combinations of root joint

configurations (i.e., any joint can be a root and

multiple roots are supported), highly efficient

computation of per-frame joint positions and

orientations, and partial motion representations. This

is only possible because we propose a more general

method of constructing transformation matrices

347

Guerra-Filho G..

A GENERAL MOTION REPRESENTATION - Exploring the Intrinsic Viewpoint of a Motion.

DOI: 10.5220/0003855303470352

In Proceedings of the International Conference on Computer Graphics Theory and Applications (GRAPP-2012), pages 347-352

ISBN: 978-989-8565-02-0

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

using pre-rotation transformations instead of the

standard post-rotation transformations in the bvh and

asf/amc formats. The main contributions of this

paper are: (1) a general motion representation that

considers multiple roots, (2) the introduction of three

operations to support this data structure (shift root,

split skeleton tree, and join skeleton trees), (3) the

procedures to convert from raw marker data or post-

rotation formats (e.g., bvh and asf/amc) to our pre-

rotation format, and (4) experimental results

showing the time and space performance of our new

motion representation. At the full translational

configuration, GMR is around seven times faster

than bvh. Our experiments are centered on the

rendering of joint positions. However, similar

experiments based on the computation of joint

coordinate frames are equivalent to ours since joint

coordinate frames are necessary to the rendering of

joint positions.

The remaining of this paper is organized as

follows. Section 2 presents a review on work related

to skeletal motion representation. Section 3

discusses the differences between existing post-

rotation formats (bvh and asf/amc) and our pre-

rotation format. Section 4 presents the General

Motion representation and its three operations.

Section 5 describes the generation of GMR from raw

marker data or from a post-rotation format. Section 5

summarizes the experimental results on time and

space performance comparing the bvh format and

our GMR representation.

2 RELATED WORK

Existing motion capture formats, such as bvh and

asf/amc, lack modeling flexibility by providing a

single skeletal root joint for all motions. These

formats implicitly restrict the choice of the root joint

by requiring that the root’s children behave as a rigid

body (i.e., a single rigid motion for all children of a

joint). This restriction is a consequence of the way

that local transformation matrices are composed to

derive global coordinates for joints according to

these formats. A formal proof of this fact is avoided

here due to a lack of space. However, this rigid body

constraint applies actually to any joint having more

than one child in the skeleton tree. For this reason,

artificial dummy joints are necessary to model

independent motion for multiple children of a single

joint. A simple inspection of existing motion files at

joints with more than one child, in bvh format for

example, suffices to verify the need for dummy

joints to allow independently moving joints with a

single parent. This is a significant drawback of state-

of-art motion representations by creating additional

time and space requirements and algorithmic

complications to handle exceptions and degeneracy

in motion-based techniques.

In the area of skeletal motion representations,

Brostow et al. (2004) introduced the concept of

spines in order to discover an articulated creature’s

skeleton directly from time-varying volumetric

structures. Coleman et al. (2008) introduce

staggered poses as a generalization of poses in

traditional key-framed motion. This generalization

allows for explicitly encoded timing refinements,

where each refinement is slightly offset in time. The

relationships between these timing refinements

determine how the character will pass through the

extreme values of the pose and are important for

modeling believable propagation of force and

intention through a body. Kulpa et al. (2005) created

a morphology-independent representation of

motions for interactive human-like animation. Their

aim was to enable real-time adaptive animation

using a sparse motion capture database. Unlike their

approach, our aim was to create a data structure with

the flexibility to provide multiple root joints for the

same motion.

Research has been done in the area of modeling

figures with complex skeleto-muscular relationships

based on human anatomy (Scheeper et al., 1997).

Complex motion control algorithms, which have

been developed for primitive articulated models

better suit robot-like characters than they do human

figures (Magnenat-Thalmann and Thalmann, 1991).

GMR-based skeletal models more closely resemble

actual human skeletons than post-rotation-based

skeletal models because GMR does not require

dummy skeletal joints.

3 POST-ROTATION AND

PRE-ROTATION FORMATS

Existing motion representations compose each

joint’s local transformation matrix in a post-rotation

order, which forces the children of each joint to

behave as a rigid body. Existing post-rotation

formats overcome this restriction through the use of

artificial dummy joints which corresponds to

additional time and space requirements. For

example, when the pelvis is the root joint, the left

hip joint, right hip joint, and lower back joint (the

pelvis joint’s children in the skeleton tree) cannot

move independently of one another. More

importantly, it is impossible to make any desired

GRAPP 2012 - International Conference on Computer Graphics Theory and Applications

348

joint the skeletal root when using a post-rotation

format. For example, if the neck joint were to be the

root, then the head, left shoulder, and right shoulder

would not be able to move independently unless a

cumbersome scheme with artificial dummy joints is

used, which is clearly a problem.

To remedy the limitations of post-rotation

formats, GMR composes each joint’s local

transformation matrix in a pre-rotation order that

allows for any joint to be a root. We describe the

post-rotation and pre-rotation concepts below.

3.1 Global Transformation Matrices

Here we describe the general approach for

composing a joint’s global transformation matrix

from local transformation matrices. Let d indicate

the depth of joint j, p(j) indicate the parent of joint j,

and p

(j) indicate the kth ancestor of joint j. Note that

the root joint is denoted by p

(j). Let L

and M

indicate the local and global transformation matrices

for joint j, respectively. Let G

indicate the

transformation matrix with just the global offset of

the skeleton. Then,

( j)

...L

( j)

p( j)

(1)

Let P

indicate the 3-dimensional, homogeneous

position of joint j described by multiplying M

with

the origin of the world coordinate system:

= M

0001

[]

Also, let

indicate the 3x3 identity matrix, and

o indicate the zero column-vector,

o = 000

[]

3.2 Post-rotation Order

The bvh and asf/amc formats use the post-rotation

order of composing local transformation matrices, as

shown in the following equation,

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

111

(2)

where R

and t

are the rotation matrix and the offset

for joint j.

From Equations (1) and (2), note that the rotation

is not applied to the joint j. Consider the root r of

a skeleton tree, the root’s rotation is the only rotation

that is applied to its children, which means that each

of the root’s immediate children cannot rotate

independently of one another. Hence, the root and its

immediate children behave as a rigid body. This

constraint is valid for any joint with more than one

child in the skeleton tree.

This behavior limits the flexibility of all post-

rotation formats because only certain joints can be

roots. That is, any joint with more than a single

child, where its immediate children do not behave as

a rigid body, cannot be a root. For example, the neck

joint cannot be a root.

3.3 Pre-rotation Order

The pre-rotation order of composing local

transformation matrices is shown in the following

equation,

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

111

jjj

tRR

(3)

where R

and t

are defined as in the post-rotation

order. Equation (3) removes the restriction that a

root and its children must behave as a rigid body.

Intuitively, GMR gains this flexibility because each

joint possesses its own independent rotation that is

applied to both its children and itself.

4 THE GENERAL MOTION

REPRESENTATION

The GMR format is structurally similar to post-

rotation formats. A GMR file begins with a joint-

based skeleton specification, with frame motion data

following after. Each joint specifies a static offset

from its parent joint, a list of required rotation

channels (x-rotation, y-rotation, z-rotation), and a list

of optional translation channels (x-translation, y-

translation, z-translation). The order of the rotation

channels specifies the order in which the rotation

matrix should be composed.

4.1 GMR Operations

GMR has three basic operations that allow the

conversion of a motion from a fully rotational

representation to a fully translational representation,

and all representations in between. We present the

correctness proof for each operation in the

supplemental material.

Now, we need a way to differentiate between

symbols before and after one of the three GMR

operations is applied. Let every symbol X

indicate a

value before an operation is applied, and every

symbol X

’

indicate a value after an operation is

A GENERAL MOTION REPRESENTATION - Exploring the Intrinsic Viewpoint of a Motion

349

applied, where X is a rotation matrix, a translation

vector, a local transformation matrix, or a global

transformation matrix.

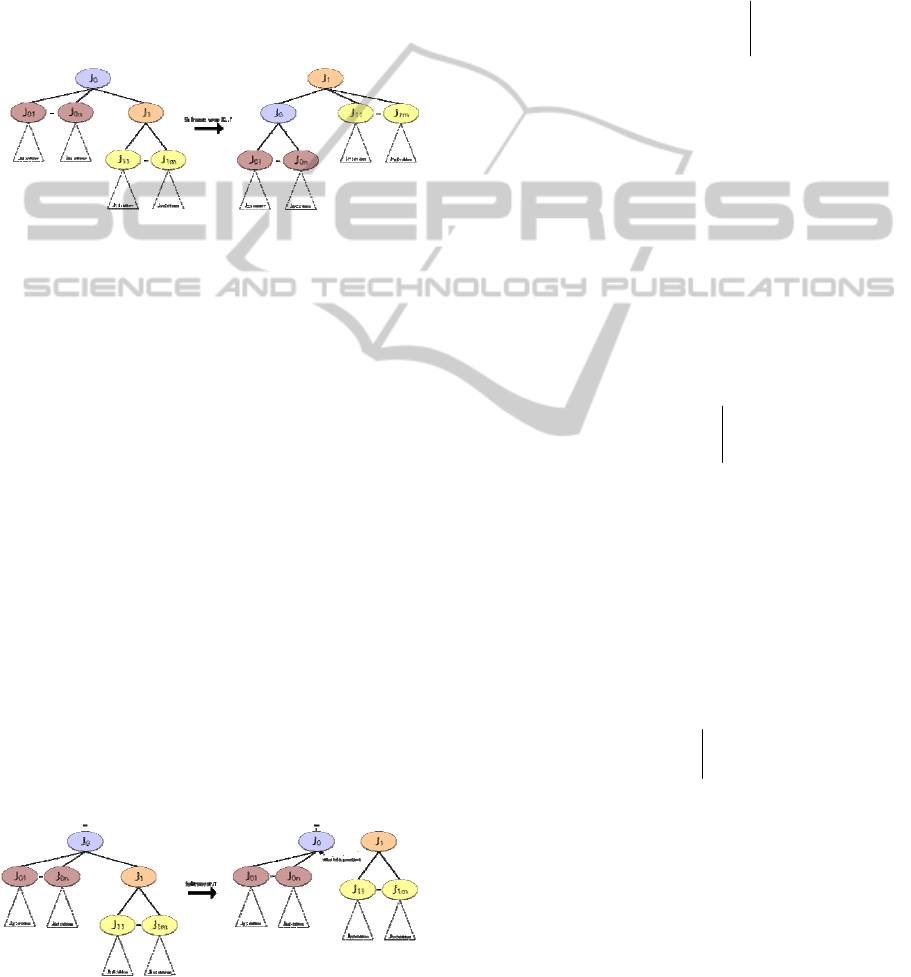
4.1.1 Shift Root Operation

The shift root operation is essentially a rotation of

the skeleton tree, meaning that it swaps the existing

root and one of its immediate children (see Figure

1). The repeated application of this operation allows

for shifting the root to any desired joint in the

skeleton tree.

Figure 1: The skeleton tree before and after the shift root

operation.

Using the notation defined in Section 3.2, we

specify the solution for the shift root operation

below. The following values should be recomputed

for each frame of the motion:

= R

+ t

= R

= o

= R

=−t

= R

−1

= t

1 j

= R

1 j

= t

1 j

4.1.2 Split Tree Operation

The split tree operation creates an additional root by

promoting an arbitrary joint to root status (see

Figure 2). Repeated applications of this operation

allow the conversion to a fully translational

representation. That is, this operation allows for a

representation where all joints are roots with 3D

Cartesian coordinates. Intuitively, a skeleton with n

joints may be represented as a single tree with n

joints or as a forest with n trees with a single joint.

Figure 2: The skeleton trees before and after the split tree

operation.

Let J

be the joint to promote to root status and J

the parent of J

. J

may or may not have a parent

joint. Note that the original tree structure is

preserved by a “soft” link from J

to its original

parent, J

. This link is necessary in order to undo

this split tree operation in the join tree operation

described next.

The global transformation matrix, M

, for J

before the split operation is

⎥

⎦

⎤

⎢

⎣

⎡

...

101

LLLGM

(4)

where G

is the transformation matrix with the

global offset of the skeleton, L

is the local

transformation matrix for the root joint, R

is the

rotation matrix associated with M

, and t

is the

translation vector associated with M

. The

calculation of J

’s global transformation matrix

changes after promoting J

to root status, so

LGM =

(5)

However, the global transformation matrix M

’

must be equal to M

, so that we avoid changing the

local transformation matrix for each child of J

. This

allows us to set Equation (4) equal to Equation (5):

⎥

⎦

⎤

⎢

⎣

⎡

LGM

(6)

Factoring Equation (6) and using the notation

defined in Section 3.2, we specify the solution for

the split tree operation. Note that, before the split, J

did not possess a global translation, but after the

split, it does. The following values should be

recomputed for each frame of the motion:

= R

= o

⎡

⎣

⎢

⎤

⎦

⎥

4.1.3 Join Trees Operation

The join trees operation is the inverse of the split

tree operation. Where the split tree operation

promotes an arbitrary joint to root status, the join

trees operation demotes a root to a non-root joint

status (see Figure 3). This operation fails if applied

to the last remaining root, which is intuitively

correct because a skeleton cannot have zero roots.

GRAPP 2012 - International Conference on Computer Graphics Theory and Applications

350

Figure 3: The skeleton trees before and after the join tree

operation.

Let J

be the joint to demote and J

be the

original parent of J

before a split operation. J

may

or may not have a parent joint. The global

transformation matrix M

for J

...LLGM

(7)

From the solution to the split operation, we know

that

= M

. Also, applying the concept that a

joint’s global transformation matrix may be

constructed incrementally by multiplying the parent

joint’s global transformation matrix with the current

joint’s local transformation matrix, we have,

. Moreover, since

= M

, we have,

110

MLM =

is the matrix that we are solving for to undo

the effects of the split operation. Solving for L

, we

have,

= M

−1

. Furthermore, we make the

following definitions:

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

Applying the pre-rotation form of constructing

local transformation matrices from Equation (3), we

have,

⎥

⎦

⎤

⎢

⎣

⎡

111

tRR

Now, we specify the final solution to the join

trees operation. The following values should be

recomputed for each frame of the motion:

= R

−

= R

−1

− t

)

5 GMR GENERATION

Ideally, GMR should be generated directly from

marker-data obtained in the motion capture process.

In this case, GMR will use the simplest, most

intuitive skeleton hierarchy possible, avoiding the

use of dummy joints. The conversion from post-

rotation formats, such as bvh and asf/amc is

possible, but preserves undesirable artifacts of the

post-rotation formats, such as the dummy joints.

5.1 From Marker Data

To convert directly from raw marker data to GMR,

first we have to find the global transformations for

the parent bone’s coordinate system and the child

bone’s coordinate system. If we let M

represent the

global transformation for the child bone and let M

p(c)

represent the global transformation for the parent

bone, then to compute the incremental

transformation from the parent coordinate system to

the child coordinate system we construct the

following equation,

ccpc

LMM

)(

In the above equation,

is the local

transformation matrix for the child bone. The

derivation of

is nearly identical to the derivation

of the solution for the GMR join trees operation and

has been omitted for the sake of brevity.

5.2 From a Post-rotation Order

Representation

It is also possible to convert directly from a post-

rotation order format, but doing so preserves

undesirable features of the original formats. For

example, a direct conversion from bvh to GMR

preserves all joints, even the joints that are no longer

required, such as the dummy joints contained in the

original bvh format. An improved conversion

method should automatically detect and remove

dummy joints before creating the GMR skeleton.

However, here we include the direct conversion

method.

Let

be the root’s global transformation

matrix. We define these symbols as,

⎥

⎦

⎤

⎢

⎣

⎡

Now, let R

p(j)

indicate the rotation for the parent

of node j before conversion, where j is an internal or

leaf node. For the sake of brevity, we only include

the solution,

tt =

)(

jpj

RR =

A GENERAL MOTION REPRESENTATION - Exploring the Intrinsic Viewpoint of a Motion

351

6 EXPERIMENTAL RESULTS

We tested the time and space performance of bvh

and GMR. We constructed an experiment that

computes the position of each joint for each frame of

motion. Our motion dataset consisted of 37 distinct

bvh motion capture files with 14.223 total minutes

of motion capture data (over 100,000 frames at 120

frames-per-second). We converted each bvh file to

the GMR format, where we tested GMR

performance using an optimized rendering loop that

took advantage of translational information in root

nodes. In the best case, GMR performs around 7

times faster than bvh. The results are summarized by

the graph in Figure 4. Although the time cost is a

single microsecond per frame in our experiments,

this speed up is significant especially in the context

of applications where very limited computation

power is available such as gaming and humanoid

robotics.

The left-most GMR point on the graph contains

one single root, while the right-most GMR point on

the graph contains 26 roots. For this experiment, we

define a GMR configuration C

as a GMR

containing k roots, for k = 1, …, 26. We constructed

ten GMR instances C

for each k by selecting

random sets of k joints as roots, in order to ensure

fairness and prevent artificially inflated performance

results. We then recorded the performance of each

instance. To compute the data points on the graph

above, we averaged the recorded times for GMR

configurations with matching numbers of roots.

Figure 4: Performance of GMR configurations compared

with BVH.

7 CONCLUSIONS

We introduced the general motion representation to

consider multiple roots with the support of three

operations (shift root, split skeleton tree, and join

skeleton trees). These operations allow reduced

skeletal complexity because of the application of

pre-rotation local transformation matrices which

eliminates the requirement for dummy joints. We

also present procedures to convert from raw marker

data or post-rotation formats.

We also demonstrate the highly efficient

computation of per-frame joint positions and

orientations. Our experimental results show that

GMR outperforms traditional motion formats in both

speed and flexibility. At the full translational

configuration, GMR is around seven times faster

than bvh. These benefits make GMR a good

candidate for computationally intensive, time-

sensitive tasks such as real-time gaming

applications. With respect to alternate viewpoints,

GMR also opens many avenues of research that

were once difficult to explore. Additionally, GMR

retains the familiarity and simplicity of expression of

the BVH file format.

REFERENCES

Brostow, G., Essa, I., Steedly, D., Kwatra, V., 2004. Novel

skeletal representation for articulated creatures.

Lecture Notes in Computer Science, vol. 3023, pp.

66-78.

Coleman, P., Bibliowicz, J., Singh, K., Gleicher, M., 2008.

Staggered poses: A character motion representation for

detail-preserving editing of pose and coordinated

timing. In Symposium on Computer Animation, pp.

137-146.

Kulpa, R., Multon, F., Arnaldi, B., 2005. Morphology-

independent representation of motions for interactive

human-like animation. Computer Graphics Forum,

vol. 24, pp. 343-351.

Magnenat-Thalmann, N., Thalmann, D., 1991. Complex

models for animating synthetic actors. IEEE Computer

Graphics and Applications, vol. 11, no. 5, pp. 32-44.

Scheepers, F., Parent, R., Carlson, E., May, S., 1997.

Anatomy-based modeling of the human musculature.

In Annual Conference on Computer Graphics and

Interactive Techniques, pp. 163-172.

GRAPP 2012 - International Conference on Computer Graphics Theory and Applications

352